Students can Download Karnataka SSLC Maths Model Question Paper 3 with Answers, Karnataka SSLC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus SSLC Maths Model Question Paper 3 with Answers
Time: 3 Hours
Max Marks: 80
I. In the following questions, four choices are given for each question, choose and write the correct answer along with its alphabet: ( 1 × 8 = 8 )
Question 1.
In the following numbers, irrational number is
a) 0.232332333……
b) 0.23233
c) 0.232323
d) 0.2323
Answer:
a) 0.232332333……
Question 2.
10 sec2A – 10tan2A =
a) sec2A
b) 10
c) 1
d) 0
Answer:
b) 10
Solution:
10 sec2A – 10tan2A
10(sec2A – tan2A) = 10(1)= 10
Question 3.
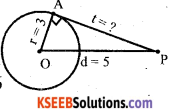
The length of the tangent drawn to a circle of radius 3cm from 5cm away from the centre is
a) 4cm
b) 5cm
c) 3cm
d) 2cm 4
Answer:
a) 4cm
Solution:
d2 = r2 + t2
t2 = d2 – r2
52 – 32
= 25 – 9
∴ t = 16 = 4cm
Question 4.
A solid piece of copper of dimension 24 × 49 × 33 cms is moulded and recast into a sphere. The radius of the
sphere formed is ________
a) 49 cm
b) 24 cm
c) 21 cm
d)33 cm
Answer:
e) 21 cm
l × b × h = \(\frac{4}{3} \pi r^{3}\)

![]()
Question 5.
The degree of the polynomial in the graph given below is
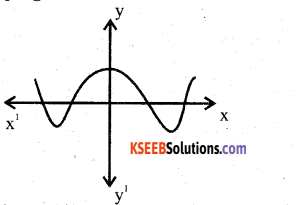
a) 4
b) 3
c) 1
d) 2
Answer:
a) 4
Solution:
4 since it is intersecting the x – axis at 4 points.
Question 6.
The sum of the n terms of an AP is 2n2 + 5n and its common difference is 6, then its first term is
a) 0
b) 5
c) 2
d) 7
Answer:
d) 7
Solution:
Sn = 2n2 + 5n
S1 = 2(1)2 + 5(1)
= 2 + 5 = 7
![]()
Question 7.
In ∆ PQR, PR = 12cm, QR = 6√3 cm, PQ = 6cm. The angle Q is
a) 45°
b) 90°
c) 30°
d) 120°
Answer:
b) 90°
Solution:
PR2 = PQ2 + QR2
122= (6√3 )2 + 62
144 = 108 – 36
144=144
∴ ∠Q = 90°
Question 8.
A cube numbered 1 to 6 is thrown once, the probability of getting a number divisible by 3 is
a) 2/3
b) 0
c) 1/3
d) 1
Answer:
Event A = {3,6}
n(s) = 6, n(A) =2
P(A) = \(\frac{n(A)}{n(S)}=\frac{2}{6}=\frac{1}{3}\)
II. Answer the following Questions : (1 x 8 = 8)
Question 9.
Given g(x) = 2x + 1, q(x) = (x3 + 3x2 – + 1), r(x) = 0, Find p(x)
Answer:
p(x) = g(x) q(x) + r(x) 1 650 1170
= (2x + 1) (x3 + 3x2 – x + 1) + 0
p(x) = 2x (x3 + 3x2 -x + 1) + 1(x3 + 3x2 – x + 1)
= 2x4 + 6x3 – 2x2+ 2x + x3 + 3x2 – x + 1
= 2x4 + 7x3 + x2 + x + 1
Question 10.
If the sum of first n odd natural number is 1225, find the value of n.
Answer:
Sum of “n” odd natural number = n2 = 1225
n = √1225
n = 35
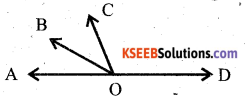
Question 11.
In the fig. ∠AOD is divided into 2 parts which are in A.P. the smallest angle ∠AOB = 20° . Find the common difference between each angle.
Answer:
∠AOB +∠BOC + ∠COD = 180°
a + a + d + a + 2d= 180°
3a + 3d= 180°
3(20) + 3d = 180°
60 + 3d = 180°
3d = 180 – 60
d = 120/3 = 40°
Question 12.
In ∆ ABC, if DE || BC, then \(\frac{\mathbf{A B}}{\mathbf{A D}}=\frac{\mathbf{A C}}{\mathbf{A} \mathbf{E}}=\frac{\mathbf{B C}}{\mathbf{D E}}\) , state the theorem to justify this.
Answer:
In a triangle, if a line is parallel to one of the sides then the sides of given triangle are propotional to sides of the intercepted triangle.
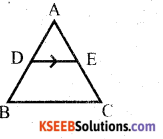
Question 13.
Find the largest number which divides 650 and 1170.
Answer:
H.C.F of (650, 1170) = 130
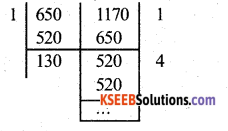
![]()
Question 14.
If sin θ = 7/25, cos θ = 24/25 find the value of sin2 θ + cos2 θ
Answer:
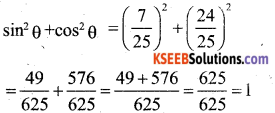
Question 15.
Find the value of cos60° cos 30° sin60° sin 30°
Answer:
cos 60° cos30 – sin 60 sin 30
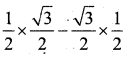
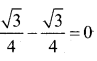
OR
This is in the form of
cos A cos B – sin A sin B = cos (A + B)
cos 60 cos 30 – sin 60 sin 30
= cos (60 + 30)
= cos (90)
– =0
Question 16.
The T.S.A of a solid hemisphere of radius 21 mm.
Answer:
T.S.A of hemisphere = 3 πr²
= 3 × \(\frac{22}{7}\) × 21 × 21 = 4158 mm2
III. Answer the following : ( 2 x 8 = 16 )
Question 17.
Prove that if x and y are odd positive integers, then x2 + y2 is even but not divisible by 4.
Answer:
Let x = 2m + 1 and y = 2n + 1 for some integers m and n.
x2 + y2 = (2m + 1)2 + (2n + l)2
x2 + y2 = 4m2 + 4m + 1 + 4n2 + 1 + 4n
= 4m2 + 4n2 + 4m + 4n + 2.
x2 + y2 = 4(m2 + n2) + 4 (m + n) + 2
x2 + y2 = 4 {(m2 + n2) + (m + n)} +2
x2 + y2 = 4q + 2, where q = (m2 + n2 ) + (m+n)
⇒ x2 + y2 is even and leaves the remainder 2 when divided by 4.
⇒ x2 + y2 is even but not divisible by 4.
Question 18.
Solve : 100x + 200y = 700
200x + 100y = 800
Answer:
Consider 100x + 200y = 700 ….(1)
200x + 100y = 800 ….(2)
Add (1) & (2) 300x + 300y= 1500
Divide by 300, x + y = 5 …… (3)
Subtract (1) and (2)
-100x + 100y= -100 Divide by 100.
-x + y = -1 …(4)
Solve (3) and (4)

y = 2
Substitute the value of y in equation (3)
x + y = 5
x + 2 = 5
x = 5 – 2 = 3
x = 3
![]()
Question 19.
Find the roots of the quadratic
equation 3x2 – 2√6x + 2 = 0 by formula method.
Answer:

Question 20.
Find the value of x in which the points (1, -1) (x, 1) and (4, 5) are collinear.
Answer:
A(1, -1) B(x, 1)C(4,5)
Area of the triangle = 0, when points are collinear.
0 = x1(y2 – y3) + x2(y3 – y1) + x3 (y1 – y2)
0 = (1) (1 – 5) + x(5 + 1) + 4(-1 – 1)
0 = -4 + 6x – 8
6x – 12 = 0
x = 12/6
x = 2
Question 21.
ABC is a right angled triangle, having [B = 90°. If BD = DC, Show that AC2 = 4AD2 – 3AB2
Answer:
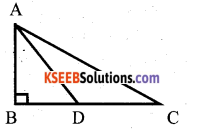
AC2 = AB2 + BC2 (Pythagoras)
AC2 = AB2 + 2(BD)2
AC2 = AB2 + 4BD2
In right angled ∆ ABD,
AD2 = AB2 + BD2
BD2 = AD2 – AB2
Consider AC2 = AB2 + 4BD2
= AB2 + 4(AD2 – AB2)
= AB2 + 4AD2 – 4AB2
= – 3AB2 + 4AD2
= 4 AD2 – 3AB2
AC2 = 4 AD2 – 3AB2
OR
Prove that area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
Answer:
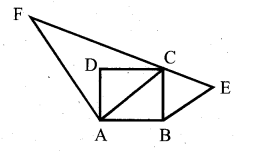
Data : ABCD is a square.
Equilateral triangles ∆ BCE and ∆ ACF have been described on side BC and diagonal AC respectively.
T.P.T. : Area of ( ∆ BCE) = 1/2 Area of ∆ ACF
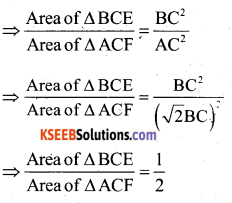
Proof : Since ∆ BCE and ∆ ACF are equilateral.
∴ They are equiangular.
∆ BCE ~ ∆ ACF
Question 22.
A box contains 90 dices which are numbered from 1 to 90. If one dise is drawn at random from the box, find the probability that it bears
(i) two digit number
(ii) a perfect square number.
Answer:
The numbers in the dise form the sample space
S = {1,2, 3,4,…….. 90}
One dise can be drawn out of 90 in 90 ways. .
n(s) = 90
i) There are 90 -9 = 81, two digit numbers, out of which one dise can be drawn in 81 ways.
∴ n(A) = 81
P(A) = \(\frac{n(A)}{n(S)}=\frac{81}{90}=\frac{9}{10}\)
ii) The perfect square numbers are B= {1,4,9, 16,25,36,49,64,81}
∴ n(B) = 9
P(B) = \(\frac{n(B)}{n(S)}=\frac{9}{90}=\frac{1}{10}\)
Question 23.
Draw a pair of tangents to a circle of radius 5cm which are inclined to each
other at an angle of 60°.
Answer:
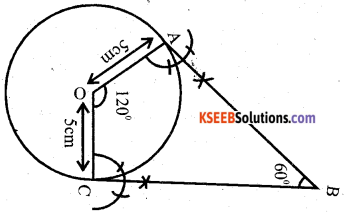
Question 24.
Prove that \(\frac{\tan \theta+\sin \theta}{\tan \theta-\sin \theta}=\frac{\sec \theta+1}{\sec \theta-1}\)
Answer:

OR
Prove that (cosecθ – cotθ)2 = \(\frac{1-\cos \theta}{1+\cos \theta}\)
Answer:
Consider (cosecθ – cotθ)2

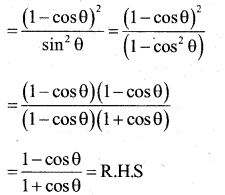
![]()
IV. Answer the following : ( 3 × 9 = 27 )
Question 25.
The sum of the ages of A and B is 85 years. 5 years ago, the age of A was twice that of B. Find the present ages.
Answer:
Let the present age of A be x years.
Let the present age of B be y years.
Sum of their ages = 85 x + y = 85 …….. (1)
Five years back, age of A was (x – 5) and that of B was (y – 5).
The age A is twice that of B.
∴ x – 5 = 2(y – 5) ……(2)
x – 5 = 2y – 10
x – 2y = -10 + 5
x – 2y = -5 ……(2)
Solve (1) and (2)
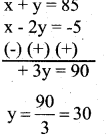
Substitute y in (1)
x + y=85
x + 30 = 85
x = 85 – 30 = 55
x = 55
∴ Present age of A is 55 years and B = 30 years.
OR
A piece of work can be done by 2 men and 7 boys in 4 days. The same piece of work can be done by 4 men and 4 boys in 3 days. How long it would take to do the same work by one man or one boy?
Answer:
Let x and y be the number of days in which one man can complete the work.
∴ In 1 day a man can do 1/x th work and
In 1 day a man can do 1/y th work.
2 men and 7 boys can complete the work in 4 days.
∴ They can complete in 1/4 th of the work in one day.
∴ \(\frac{2}{x}+\frac{7}{y}=\frac{1}{4}\) …… (1)
4 men and 4 boys together complete the work in 3days, and they can complete it in 1/3 rd of work.

4(2y + 7x) = xy
8y + 28x = xy …….(3)
3(4y + 4x) = xy
12y + 12x = xy ……..(4)
Solve (3) and (4)
(8y + 2x = xy) x 12
(l2y+ 12x = xy) x 18
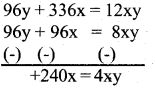
4 y = 240
y = 240/4
y = 60
3(4y + 4x) xy
12y+12x = xy ………..(4)
4y = 240
y = 240/4 = 60
Substitute y in equation (3)
8y + 28x = xy
8(60) + 28x = xy
480 + 28x = x(60)
480 + 28x = 60x
480 = 60x – 28x
480 = 32x
x = \(\frac{480}{32}=\frac{120}{8}=\frac{30}{2}\) = 15
x = 15
Thus, one man can complete the work in 15 days and one boy can do the work in 60 days.
Question 26.
Find the zeroes of the polynomial p(y) = y3 – 5y2 – 2y + 24 if it is given that Sum of the two zeros is Answer:
Let α, β,γ be the zeros of the given polynomial.
p(y) = y3 – 5y2 – 2y + 24
α + β = 7
Sum of the zeros
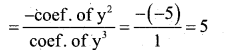
α + β + γ = 5
7 + r = 5
r = 5 – 7 = -2
r = -2
Sum of product of zeroes taken two at a
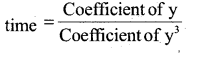
αβ + βr + rα = -2/1 = – 2
αβ + r(β + α) = -2
αβ + (7) (-2) = -2
αβ-14 = -2
αβ = -2+ 14
αβ = 12
(α – β )2 = (α + β)2– 4αβ
= (7)2 – 4(12)
(α – β)2 = 49 – 48
α – β = ±1
Solve for α and β. When α – β = +1
α + β = 7
α – β = 1
2α =8
α = 8/2 = 4
α = 4
Substitute the value of a in α + β =7
4+p =7
β =7-4 = 3
β = 3
Solve for α and β when α – β = -1
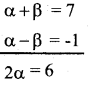
α = 6/2 = 3
α = 3
α + β = 7
3 + β=7
β = 7 – 3
a + β = 7
β = 4
When α – β = 1,
the values are α = 4, β = 3, r = -2.
When α – β = -1,
The values are α = 3, β = 4, r = -2.
Question 27.
The diagonal of a rectangular field is 60 metres more than the shorter side, if the longer side is 30 metres more than the shorter side, find the sides of the field.
Answer:
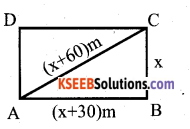
Let the shorter D side be x mtr.
Longer side is 30m more than the shorter side. A Longer side = (x + 30)m.
Diagonal is 60m more than the shorter side.
Diagonal = (x + 60) m
AC2 = AB2 + BC2 (Pythagoras)
(x + 60)2 = (x + 30)2 + x2
x2+(60)2 + 2x (60) = x2 + (30)2 + 2(x)(30)+ x2
x2 + 3600 + 120x = x2 + 900 + 60x + x2
-x2 + 60x + 2700 = 0
x2 – 60x – 2700 = 0
x2 – 90x + 30x – 2700 = 0
x(x – 90) + 30(x – 90) = 0
(x – 90) (x + 30) = 0
x – 90 = 0 or x + 30 = 0
x = 90 or x = – 30
∴ Shorter side = 90m = BC = x
Longer side = x + 30 = 90 + 30 = 120m
Diagonal = x + 60 = 90 + 60 = 150m
OR
Sum of the areas of two squares is 468m2. If the difference of their perimeters is 24m, find the sides of two squares.
Answer:
Let the sides of the two squares be x&y. Sum of the areas of two squares = 468
x2 + y2 = 468 ……(1)
Difference of their perimeters = 24m.
4x – 4y = 24 x – y = 6
x = 6 + y …….(2)
Substitute the value of x in (1)
x2 + y2 = 468
(6 + y)2 + y2 = 468
36 + y2+ 12y + y2 = 468
2y2 + 12y + 36 = 468
Divide by 2
y2 +6y+ 18 = 234 y2 + 6y = 234 – 18
y2 + 6y – 216 = 0
y2+18y – 12y -216 = 0
y(y + 18)-12(y + 18) = 0
(y + 18) (y – 12) = 0
y+18 = 0, y -12 = 0
y = -18,y = 12
∴ x = 6+y = 6 + 12 = 18m
The sides of two squares are 18m and 12m.
![]()
Question 28.
Show that the points x(2, -2) y(-2, 1) and z(5, 2) are the vertices of a right angled triangle XYZ and also calculate its area.
Answer:
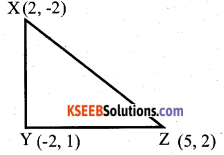

⇒ XYZ is an isosceles right angled triangle.
Area of a right angled triangle = \(\frac{1}{2}\) x base x height
\(\frac{1}{2}\) × 5 × 5 = \(\frac{25}{2}\) = 12.5 cm
OR
Find the values of k for which the points A(k + 1, 2k) B(3k, 2k+3) and C(5k – 1, 5k) are collinear.
Answer:
A(k + 1, 2k) = (x1, y1)
B(3k, 2k + 3) = (x2, y2)
C(5k-1, 5k) = (x3, y3)
Area of the triangle = 0, for the points to be collinear.
Area =[x1(y2 – y3) + x2(y3-y1) + x3(y1-y2)]
0 = \(\frac{1}{2}\){(k + 1) (2k+3 – 5k)+3k(5k- 2k) + (5k-1) [2k-2k-3]}
0= \(\frac{1}{2}\)]{(k+ 1) (-3k+ 3) + 3k (3k) + (5k- I)(-3)i
0 =\(\frac{1}{2}\){-3k2-3k + 3k + 3 + 9k2 – 15k+3}
0= \(\frac{1}{2}\){6k2– 15k + 6}
0 = 6k2 – 15k + 6
Divide by 3
2k2 – 5k + 2= 0
2k2 – 4k – 1k + 2 = 0
2k(k – 2) -1(k – 2) = 0
(k – 2) (2k -1) = 0
k – 2 = 0, or 2k- 1=0
k = 2 or k = 1/2
Question 29.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Answer:
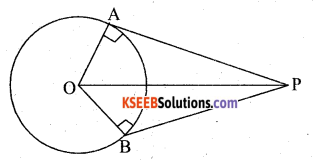
Data: ‘O’ is the centre of the circle PA and PB are the two tangents drawn from an external point P. OA and OB are radii of the circle.
To prove that: ∠APB+ ∠AOB = 180°
Proof: In AAPO and ABPO
∠OAP = ∠OBP = 90°
(∵ Angle between the radius and tangent at the point of contact is 90°)
OP = OP (∵ Common side)
OA = OB (∵ Radii of the same circle) According to RHS postulate AAPO ABPO
∠OAP = ∠OBP = 90°
∠OAP + ∠OBP = 90° + 90° = 180°
⇒ Opposite angles of OAPB quadrilateral are supplementary
∴ OAPB is a cylic quadrilateral
⇒ ∠APB + ∠AOB = 180°
![]()
Question 30.
Find the area of the shaded region where a circular arc of Radius 6 cm has been drawn with the vertex ‘O’ of an equilateral Triangle OAB of side 12cm as centre.
Answer:
Area of the shaded Region = Area of circle area of sector OCDE + Area of equilateral
∆ le OAB
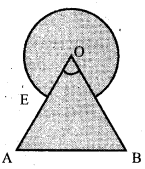
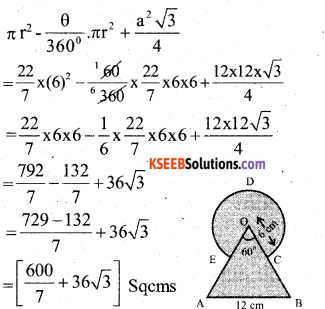
OR
From each corner of a square of side 4cm a quadrant of a circle of radius 1cm is cut and also a circle of diameter 2cm is cut as shown in Fig, Find the area of the remaining portion of the square.
Answer:
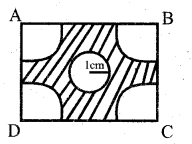

Area of shaded region = Area of square – (Area of circle + Area of 4 quadrants)
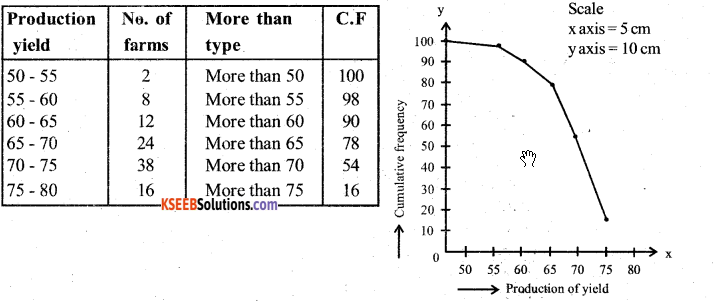
The following table gives production yield per hectare of wheat of 100 farms of a
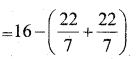
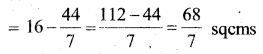
Question 31.
The following table gives production yield per hectare of wheat of 100 farms of a
village.

Change the distribution to a more than type distribution and draw its ogive.
Answer:
Question 32.
If the median of the distribution given below is 28.5. Find the valucs of x and y.
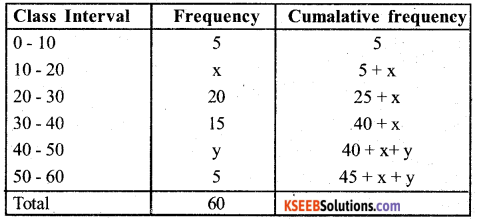
Answer:
Meadian = 28.5, lies in the C.I , 20 – 30
The median class = 20 – 30
l = 20, f = 20, c.f = 5 + h, h = 10, n = 60
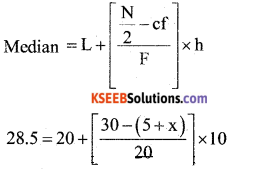
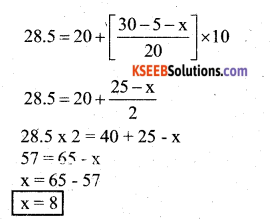
![]()
Question 33.
Construct a triangle ABC with side BC = 7cm, ∠B = 45°, ∠C = 105°. Then construct a triangle whose sides are 4/3 times the corresponding sides of ∆ ABC.
Answer:
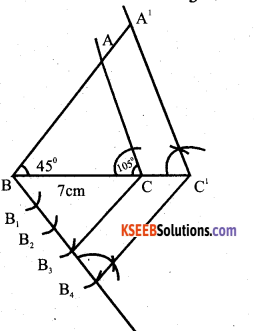
V. Answer the following ( 4 × 4 = 16 )
Question 34.
Solve the pair of equations graphically.
x+y=3 and 3x-2y=4
Answer:
x + y = 3
y = 3- x
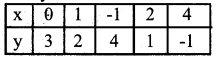
3x – 2y = 4
-2y = 4 – 3x .
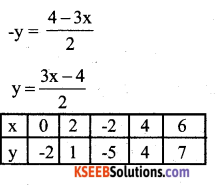
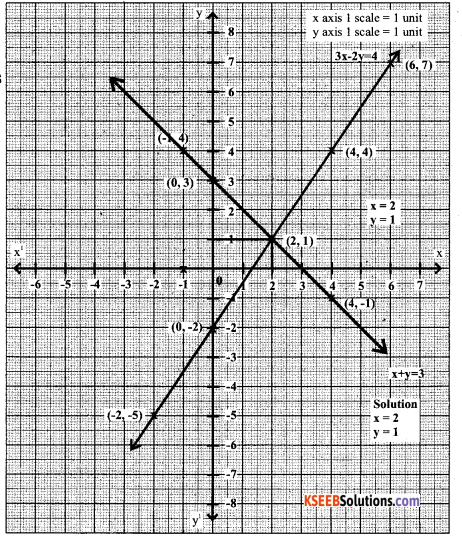
Question 35.
If the sum of first 8 terms of an Arithmetic progression is 136 and that of first 15 terms is 465, then find the sum of first 25 terms.
Answer:
Given S8 = 136, S15 = 465, S25 = ?
Use the formula Sn = \(\frac{n}{2}\) [2a + (n -l)d]
s8 = \(\frac{8}{2}\)[2a + (s-l)d]
136 = 4 (2a + 7d)
∴ 2a + 7d = 136/4
2a + 7d= 34…….(1)
S15 = \(\frac{15}{2}\)[2a + (15-l)d]
465 = \(\frac{15}{2}\)[2a + 14d]
465= \(\frac{15}{2}\) x 2(a + 7d)
∴ a + 7d = 465/15
a + 7d = 31 …….(2)
From (1) and (2)
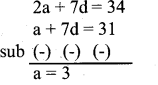
Consider a + 7d = 31
3 + 7d = 31
7d = 31 – 3
d = 28/7
d = 4
∴S25 = \(\frac{25}{2}\)[2a + (25-1)d]
S25 = \(\frac{25}{2}\)[2a + (25-1)d]
S25 = \(\frac{25}{2}\)[2a + (24)d]
S25 = \(\frac{25}{2}\)[2(3) + 24(4)d]
S25 = \(\frac{25}{2}\) × 102
S25 = 1275
‘5 ‘ 9
OR
The sum of the 5th and 9th terms of an A.P is 40 and the sum of the 8th and 14th term is 64. Find the sum of the first 20 terms.
Answer:
Given T5+ T9 = 40 and T8 + T14 = 64
a + 4d + a + 8d=40
2a + 12d = 40….(1)
a + 7d + a + 13d = 64
2a + 20d = 64…. (2)
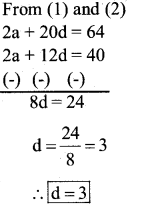
Consider 2a + 12d = 40
2a + 12(3) = 40
2a + 36 = 40
2a = 40 – 36
a = 4/2
a = 2
Sn = \(\frac{n}{2}\)[2a + (n-1)d]
S20 = \(\frac{20}{2}\)[2(2) + (20-1)3]
= 104(4 + 57)
= 10 × 61
= 610
![]()
Question 36.
Two poles of equal heights are standing opposite to each other on either side of the road, which is 80m wide. From a point between them on to the road, the angles of elevation of the top of the poles re 60 and 30’, respectively. Find the height of the poles and distances of the point from the poles.
Answer:
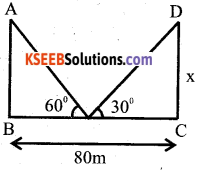
In ∆ ABE.
tan60 = \(\frac{\mathrm{AB}}{\mathrm{BE}}\)
√3 = x/BE
x = √3BE ….. (1)
tan30 = DC/EC
\(\frac{1}{\sqrt{3}}=\frac{x}{E C}\)
EC = x√3
EC = BE × √3 .√3 [∵ x = √3.BE]
FC = 3BE
∴ EC=3BF
We know that
BE + EC = 80 rn
BE 3BE 80m
4BE = 80
BE = 80/4 = 20
⇒ EC = 3BE 3(20)= 60m
∴ x = BE.
x = 20√3
⇒ AB = CD = 20√3 m
∴ The distance from the point to the pole arc 20m towards left and 60m towards the right
poles
Height of the poles 20√3m
Question 37.
Prove areas of similar triangles.
Answer:
Areas of similar triangles are proportional
to the squares on the corresponding sides.
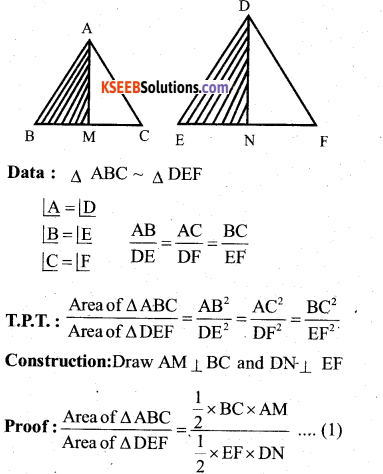
In ∆ABM and ∆DEN
∠AMB = ∠DNE = 90 [construction]
∠B =∠E (Data)
∠BAM = ∠EDN (Remainingang1e)
∆ABM ∼ ∆ DEN
∆ABM & ∆DEN are equiangular
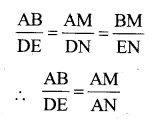

![]()
VI. Answer the following : ( 5 × 1 = 5 )
Question 38.
A circus tent is made of canvas and is in the form of a right circular cylinder and a right circular cone above it. The diameter and height of the cylindrical part of the tent are 126m and 5m respectively. The total height of the tent is 21m. Find the total cost of the canvas used to make the tent when the cost per m2 of the canvas is ?15.
Answer:
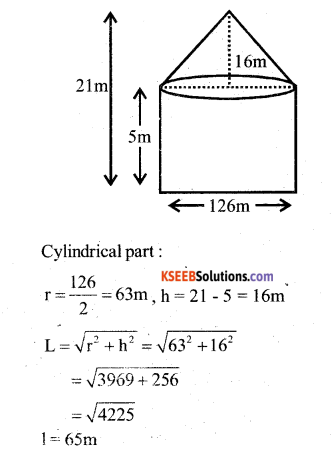
Total canvas used=CS A of cylindrical part -1- CS A of conical part
=2πrh + πrl
= 2 × \(\frac{22}{7}\) × 63 × 5 + \(\frac{22}{7}\) x 63 x 65
= 1980 m2 + 12870 m2
= 14850 m2
Total canvas used = 14850 m2
* Cost of canvas at the rate of ₹16 per m2
= 14850 × 15= ₹ 2,22.750.
Cost of canvas = ₹ 2,22,750