KSEEB SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Ex 11.1

KSEEB SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Ex 11.1 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.1.

Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.1

Trigonometry Exercise 11.1 Solutions Question 1.
In ∆ABC, right-angled at B, AB = 24 cm., BC = 7 cm. Determine:
i) sin A, cos A
ii) sin C, cos C
Solution:

In ⊥∆ABC, ∠B = 90°
As per Pythagoras theorem
AC² = AB² + BC²
= (24)² + (7) ²
= 576 + 49
AC² = 625
∴ AC = 25 cm

Introduction To Trigonometry Class 10 Exercise 11.1 Question 2.
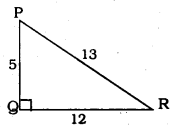
In the given figure, find tan P – cot R.
Solution:

In ⊥∆PQR, ∠Q = 90°
∴ PQ² + QR² = PR²
(12)² + QR² = (13)²
144 + QR² = 169
QR² = 169 – 144
QR² = 25
∴ QR = 5 cm.

Introduction To Trigonometry Exercise 11.1 Question 3.
If sin A = \(\frac{3}{4}\) calculate cos A and tan A.
Solution:

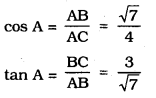
Exercise 11.1 Class 10 Trigonometry Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:

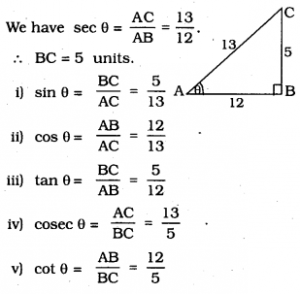
KSEEB Solutions For Class 10 Maths Trigonometry Question 5.
Given sec θ = \(\frac{13}{12}\), calculate all other trigonometric ratios
Solution;

10th Maths Introduction To Trigonometry Exercise 11.1 Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:
In ⊥∆ABC, ∠A and ∠B are acute angles. CD ⊥ AB is drawn.

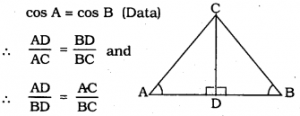
CD is common.
S.S.S. Postulate :
∴ ∆ADC ~ ∆ADB
∴ ∠A = ∠B
∵ “Angles of similar triangles are equiangular.”

10th Class Maths Trigonometry Exercise 11.1 Question 7.
If cot θ = \(\frac{7}{8}\), evaluate :
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot²θ
Solution:

Trigonometry Class 10 Exercise 11.1 Question 8.
If 3 cot A = 4, check whether \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos² A – sin² A or not
Solution:

Introduction To Trigonometry Class 10 KSEEB Question 9.
In ∆ABC, right-angled at B, if tan A =\(\frac{1}{\sqrt{3}}\) find the value of:
i) sin A cos C + cos A sin C
ii) cos A cos C – sin A sin C
Solution:

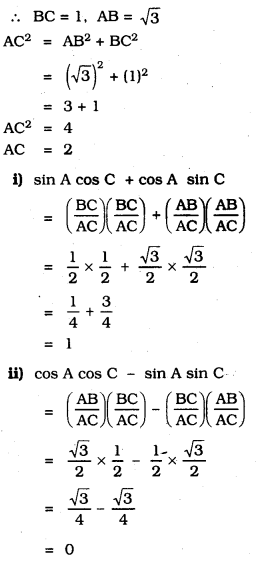
Trigonometry Ex 11.1 Question 10.
In ∆PQR, right-angled at Q, PR + QR = 25 cm. and PQ = 5 cm. Determine the values of sin P, cos P and tan P
Solution:
PQ = 5 cm
PR + QR = 25 cm
∴ PR = 25 – QR

PR² = PQ² + QR²
QR² = PR² – PQ²
= (25 – QR)² – (5)²
QR² = 625 – 50QR + QR² – 25
50QR = 600
∴ QR = 12 cm.
∴ PR = 25 – QR = 25 – 12 = 13 cm.
∴ QR = 12 cm
∴ PR = 25 – QR = 25 – 12 = 13 cm

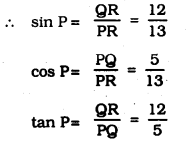
10th Class Trigonometry Exercise 11.1 Question 11.
State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
Answer:
False. 60° = \(\sqrt{3}\) > 1

(ii) If sec A = \(\frac{12}{5}\) for some value of angle A.
Answer:
True. because sec A > 1.

(iii) cos A is the abbreviation used for the cosecant of angle A.
Answer:
False. Because cos A is simplified as cos.

(iv) cot A is the product of cot and A.
Answer:
False. cot is ∠A or meaningless. Here,
cot A = \(\frac{\text { Adjacent side }}{\text { Opposite side }}\)

(v) sin θ = \(\frac{4}{3}\) for some angle θ
Answer:
False. because sin θ ≯ 1

We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Ex 11.1 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.1, drop a comment below and we will get back to you at the earliest.