Students can Download Basic Maths Exercise 18.7 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 18 Differential Calculus Ex 18.7
Part – A
2nd PUC Basic Maths Differential Calculus Ex 18.7 One Mark Questions and Answers
Question 1.
Find \(\frac{d^{2} y}{d x^{2}}\).
1. y = 3x3 + 4x2 + 7
2. y = \(\sqrt{2 x+3}\)
3. y = e3x + 2
4. y = x3 . logx
5. y = log x + ax
6. y = e-x sin 2x
7. y = log(log x)
8. y = cos 4x cos 2x
9. y = sin 3x sin 2x
10. y = cos mx sin nx
Answer:
1. Given y = 3x3 + 4x2 + 7
\(\frac{d y}{d x}\) = 9x2 + 8x
\(\frac{d^{2} y}{d x^{2}}\) = 18x + 8
2. y = \(\sqrt{2 x+3}\)

![]()
3. y = e3x + 2
\(\frac{d y}{d x}\) = 3e3x + 2
\(\frac{d^{2} y}{d x^{2}}\) = 9e3x + 2 = 9y
4. y = x3 logx
\(\frac{d y}{d x}\) = x3 . \(\frac { 1 }{ x }\) + log x . 3x2 = x2 + 3x2 log x
\(\frac{d^{2} y}{d x^{2}}\) = 2x + 3x2 \(\frac { 1 }{ x }\) + log x . 6x = 5x + 6x log x
5. y = log x + ax
\(\frac{d y}{d x}\) = \(\frac { 1 }{ x }\) + ax . log a
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{-1}{x^{2}}\) + log a . axlog a
= \(\frac{-1}{x^{2}}\) + ax(log a)2
6. Given y = e-x sin 2x
\(\frac{d y}{d x}\) = e-x(2 cos2x) + sin 2x .(-e-x)
= e-x( 2 cos2x – sin2x)
\(\frac{d^{2} y}{d x^{2}}\) = e-x(-4 sin 2x – 2 cos 2x) + (2 cos 2x – sin 2x) (-e-x)
= e-x [-4 sin 2x – 2 cos 2x – 2 cos 2x + sin 2x]
= e-x (-3 sin2x – 4 cos 2x)
![]()
7. y = log(log x)

8. y = cos 4x cpos 2x
y = \(\frac { 1 }{ 2 }\) (cos 6x + cos 2x)
\(\frac{d y}{d x}\) = \(\frac { 1 }{ 2 }\) (-6 sin6x – 2 sin2x) = -3 sin 6x – sin2x
\(\frac{d^{2} y}{d x^{2}}\) = -18 cos 6x – 2 cos 2x
9. Given y = sin 3x sin 2x
y = \(\frac { 1 }{ 2 }\) (cos 5x – cos 7x);
\(\frac{d y}{d x}\) = \(\frac { 1 }{ 2 }\) (-5 sin 5x + 7 sin 7x)
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac { 1 }{ 2 }\) (- 25 cos 5x + 49 cos 7x)
10. y = cosmx.sinnx
y = \(\frac { 1 }{ 2 }\)[sin (m + n)x – sin(m – n)x]
\(\frac{d y}{d x}\) = \(\frac { 1 }{ 2 }\)[(m + n)cos(m – n)x – (m – n)cos (m – n)x]
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac { 1 }{ 2 }\)[-sin(m + n)x .(m + n)2 + (m – n)2 . sin (m – n)x]
= \(\frac { 1 }{ 2 }\)[-(m + n)2 . sin (m + n)x + (m – n)2 sin(m – n)x].
![]()
Part – B
2nd PUC Basic Maths Differential Calculus Ex 18.7 Two and Three Marks Questions and Answers
Question 1.
Find \(\frac{d^{2} y}{d x^{2}}\) if.
1. x = a cos θ, y = a sin θ
2. x = a(θ + sinθ), y = a(1 – cos θ)
3. x = a cos3t, y = -a sin3t
Answer:
1. Given x = a cos θ, y = a sin θ
Differentiate both W.r.t. θ
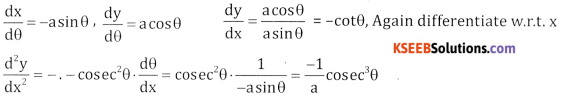
2. Given x = a(θ + sinθ), y = a(1 – cos θ)
Differentiate both w.r.t θ
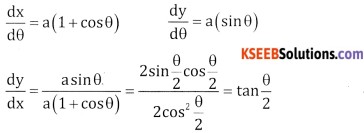
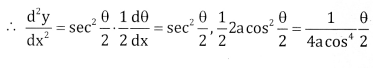
![]()
3. Given x = a cos3t, y = -a sin3t
Differentiate bpth w.r.t t
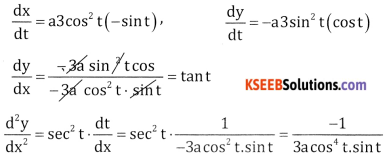
Question 2.
If y = sin mx, show that \(\frac{d^{2} y}{d x^{2}}+m^{2} y=0\)
Answer:
Given y = sin mx
\(\frac{d y}{d x}\) = -m cos mx
\(\frac{d^{2} y}{d x^{2}}\) = m2 sin mx = -m2y
∴ \(\frac{d^{2} y}{d x^{2}}+m^{2} y=0\)
![]()
Question 3.
If y = 500e7x + 600e-7x, show that \(\frac{d^{2} y}{d x^{2}}\) = 49y.
Answer:
y = 500e7x + 600e-7x
\(\frac{d y}{d x}\) = 500.7e7x + 600(-7. e-7x)
\(\frac{d^{2} y}{d x^{2}}\) = 500(49e7x) + 600(+49 .e-7x)
= 49 (5007x + 600e-7x) = 49y
∴ \(\frac{d^{2} y}{d x^{2}}\) = 49y
Question 4.
If y = eax + e-ax, Show that y2 – a2y = 0
Answer:
y = eax + e-ax
y1 = aeax – ae-ax
Y2 = a2eax + a2e-ax
= a2(eax + e-ax) = a2y
∴ y2 – a2y = 0.
Question 5.
If y = 2 + log x, show that xy2 + y1 = 0.
Answer:
yi = \(\frac { 1 }{ x }\) ⇒ xy1 = 1
∴ = xy2 + y1 = 0
![]()
Part – C
2nd PUC Basic Maths Differential Calculus Ex 18.7 Five Marks Questions and Answers
Question 1.
If x2 – xy + y2 = a2, show that \(\frac{d^{2} y}{d x^{3}}=\frac{6 a^{2}}{(x-2 y)^{3}}\)
Answer:

Question 2.
If x2 + 2xy + 3y2 = 1, show that y2 = \(\frac{-2}{(x+3 y)^{3}}\)
Answer:
x2 + 2xy + 3y2 = 1
Differentiate w.r.t x we get
2x + 2(x.y1 + y.1) + 6y.y1 = 0
y1(2x + 6y) = -2x -2y

Hence proved.
![]()
Question 3.
If y = a cos mx + b sin mx, show that \(\frac{d^{2} y}{d x^{2}}+m^{2} y=0\)
Answer:
Given y = a cos mx + b sin mx
\(\frac{d y}{d x}\) = -am sin mx + bm cos mx
\(\frac{d^{2} y}{d x^{2}}\) = -am2 cos mx – bm2 sin mx
= m2(a cos mx + b sin mx) = -m2y
⇒ \(\frac{d^{2} y}{d x^{2}}+m^{2} y=0\)
Question 4.
If y = a cos (log x) + b sin (log x), show that x2y2 + xy1 + y = 0
Answer:
y = a cos(log x) + b sin (log x)
\(y_{1}=\frac{-a \sin (\log x)}{x}+\frac{b \cos (\log x)}{x}\)
xy1 = -a sin (log x) + b cos (log x) Again diff w.r.t x
xy2 + y11 = \(\frac{-a \cos (\log x)}{x}-\frac{b \sin (\log x)}{x}\)
x2y2 + xy1 = -(a cos logx + b sin (log x)) = =y
⇒ x2y2 + xy1 + y = 0
Question 5.
If y = log (x – \(\sqrt{x^{2}+1}\)), show that (x2 + 1)y2 + xy1 = 0
Answer:
If y = log (x – \(\sqrt{x^{2}+1}\))
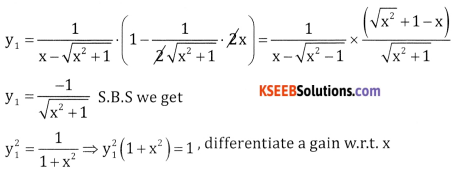
2y1 . y2(1 + x2) + y12(2x) = 0 ÷ 2y1
⇒ (1 + x2)y2 + xy1 = 0.
![]()
Question 6.
If y = x + \(\sqrt{x^{2} – 1}\) , show that (x2 – 1)y2 + xy1 – y = 0
Answer:
y = x + \(\sqrt{x^{2} – 1}\) differentiate w.r.t x
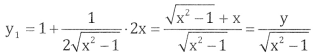
∴ (x2 – 1) y12 = y2 Differentiate agin w.r.t x
(x2 – 1)2y1y2 + y12 (2x) = 2y .y1 (÷ 2y1 we get)
(x2 – 1)y2 + xy1 – y = 0 Hence proved
Question 7.
If y = \((x+\sqrt{x^{2}+1})^{m}\) , show that (x2 + 1)y2 + xy1 – m2y = 0
Answer:
y = \((x+\sqrt{x^{2}+1})^{m}\)

(x2)y12 = m2y2 ; (x2 + 1) . 2y1y2 + y21(2x) = m2.2yy1 ÷ by 2y1
(x2 + 1)y2 + xy1 – m2 = 0
Question 8.
If y = sin(log x), show that x2y2 + xy1 + y = 0/.
Answers:
y = sin (log x)
y1 = \(\frac{\cos (\log x)}{x}\)
xy1 = cos (log x).
Again differentiate w.r.t. x
xy2 + y11 = \(\frac{-\sin (\log x)}{x}\)
x2y2 + xy1 = -y
⇒ x2y2 + xy1 + y = 0.
Follow For More:
ICICIGI Pivot Point Calculator
![]()