Students can Download Basic Maths Exercise 18.3 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 18 Differential Calculus Ex 18.3
Part – A
2nd PUC Basic Maths Differential Calculus Ex 18.3 One or Two Marks Questions and Answers
Question 1.
3x2 + 4y2 = 10
Answer:
Given 3x2 + 4y2 = 10
Diff w.r.t x
6x + 8y \(\frac{d y}{d x}\) = 0
\(\Rightarrow \quad \frac{d y}{d x}=\frac{-8 y}{6 x}=\frac{-4 y}{3 x}\)
Question 2.
\(\sqrt{x}+\sqrt{y}=3\)
Answer:

![]()
Question 3.
y2 = 4ax.
Answer:
Given y2 = 4ax.
Differentiate with respect to x
2y \(\frac{d y}{d x}\) = 4a.1 ⇒ \(\frac{d y}{d x}\) = \(\frac{4 a}{2 y}=\frac{2 a}{y}\)
Question 4.
\(x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}\)
Answer:
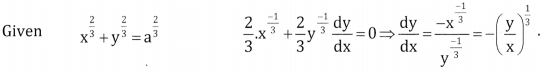
Question 5.
x2 = 4ay
Answer:
Given x2 = 4ay
Differentiate with respect to x, 2x = 4a \(\frac{d y}{d x}\) ⇒ \(\frac{d y}{d x}\) = \(\frac{2 x}{4 a}=\frac{x}{2 a}\)
Question 6.
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
Answer:
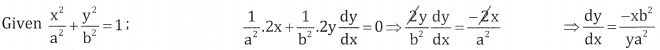
Question 7.
x3 + y3 = 3axy
Answer:
Given x3 + y3 = 3axy
3x2 + 3y2 \(\frac{d y}{d x}\) = 3a \(\left(x \cdot \frac{d y}{d x}+y \cdot 1\right)\)
\(\frac{d y}{d x}\) (3y2 – 3ax) = 3ay – 3x2 = \(\frac{d y}{d x}=\frac{a y-x^{2}}{y^{2}-a x}\)
Question 8.
x – y = 0
Answer:
Given x – y = 0
Differentiate with respect to x,
1 – \(\frac{d y}{d x}\) = 0 ⇒ \(\frac{d y}{d x}\) = 1
![]()
Question 9.
x2 – y2 = a2
Answer:
Given x2 – y2 = a2
Differentiate with respect to x we get,
2x – 2y. \(\frac{d y}{d x}\) = 0 ⇒ \(\frac{d y}{d x}\) = \(\frac{2 x}{2 y}=\frac{x}{y}\)
Question 10.
x + \(\sqrt{x y}\) = x2.
Answer:
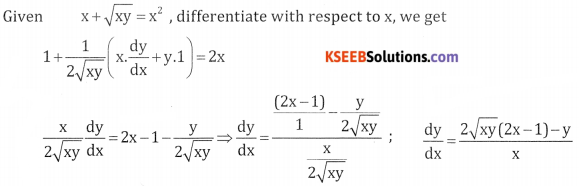
Part-B
2nd PUC Basic Maths Differential Calculus Ex 18.3 Three marks Questions and Answers
Question 1.
log(xy) = x2 + y2
Answer:
Given log(xy) = x2 + y2
log x + log y = x2 + y2 differentiate w.r.t x
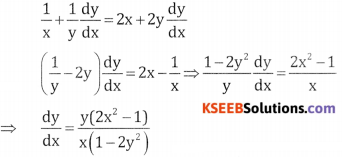
Question 2.
2x + 2y = 2x+y
Answer:
Given 2x + 2y = 2x+y
Differentiate w.r.t. x we get
2x log 2 + 2y log 2 \(\frac{d y}{d x}\)

![]()
Question 3.
xy = yx.
Answer:
Given xy = yx., taking logm both sides
y log x = x log y differentiate
Both sides w.r.t x
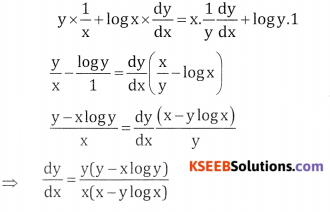
Question 4.
sin xy = cos(x + y).
Answer:
Given sin xy = cos(x + y), diff w.r.t x.
cos(xy) \(\left[\mathrm{x} \frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{y}\right]\)
\(\frac{d y}{d x}\) [sin(x + y) + xcos (xy)]
= -sin(x + y) – y cos (xy)
\(\frac{d y}{d x}=\frac{-[\sin (x+y)+\cos x y]}{(\sin (x+y)+x \cos x y)}\)
Question 5.
y = 4x+y
Answer:
Given y = 4x+y, diff. w r.t. x
\(\frac{d y}{d x}\) = 4x+y log 4(1 + \(\frac{d y}{d x}\)) = 4x+y
\(\frac{d y}{d x}\)(1 – 4x+y log 4) = 4x+y log 4
∴ \(\frac{d y}{d x}=\frac{4^{x+y} \cdot \log 4}{1-4^{x+y} \cdot \log 4}\)
![]()
Part-C
2nd PUC Basic Maths Differential Calculus Ex 18.3 Five Marks Questions and Answers.
Question 1.
If \(\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{x}}\) = a, Prove that x . \(\frac{d y}{d x}\) = y.
Answer:

Question 2.
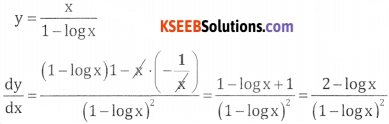
If xy = ey – x, show that \(\frac{d y}{d x}\) = \(\frac{2-\log x}{(1-\log x)^{2}}\)
Answer:
Given xy = ey – x . Taking log both sides
y log x = (y – x)log ee
x = y (1 – log x) ∵ log ee = 1
![]()
Question 3.
If cos y = x cos(a + y). show that \(\frac{d y}{d x}\) = \(\frac{\cos ^{2}(a+y)}{\sin a}\)
Answer:

Question 4.
If ex = yx show that \(\frac{d y}{d x}\) = \(\frac{(\log y)^{2}}{\log y-1}\)
Answer:
Given ex = yx Taking logm both sides
y log ee = x log y
y = x log y differentiate w.r.t x
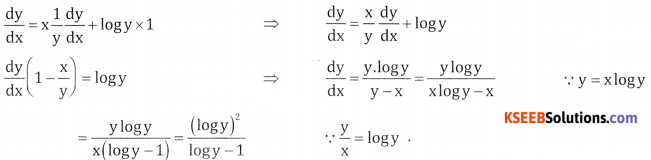
Question 5.
If ex+y = xy show that \(\frac{d y}{d x}\) = \(\frac{y(1-x)}{x(y-1)}\)
Answer:
Given yex+y = xy
Taking log m both sides
(x + y) loge = log(xy)
x+y = log x + log y diff w.r.t x

![]()
Question 6.
If yx = xy show that \(\frac{d y}{d x}\) = \(\frac{y(y=x \log y)}{x(x-y \log x)}\)
Answer:
Given yx = xy, Taking logm both sides
x log y = y log x, diff w.r.t x
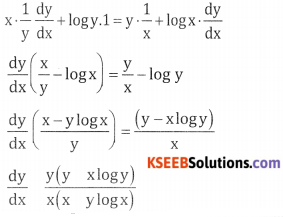
Must Read: