KSEEB SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Ex 11.2 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.2.
Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.2
Trigonometry Exercise 11.2 Solutions Question 1.
Evaluate the following :
i) sin 60° cos 30° + sin 30° cos 60°
ii) 2 tan2 45° + cos2 30° – sin2 60°

Solution:
i) sin 60° cos 30° + sin 30° cos 60°
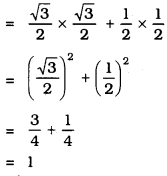
ii) 2 tan2 45° + cos2 30° – sin260°
= 2(tan 45°)2 + (cos 30°)2 – (sin 60°)2
= 2 (1)2 + \(\left(\frac{\sqrt{3}}{2}\right)^{2}-\left(\frac{\sqrt{3}}{2}\right)^{2}\)
= 2 × 1
= 2
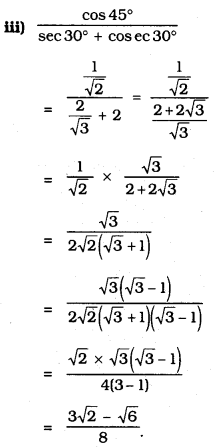
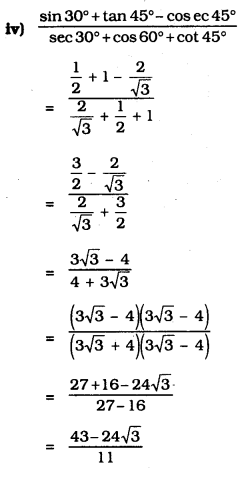
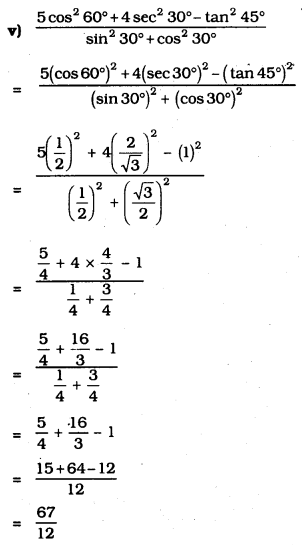
Exercise 11.2 Class 10 Trigonometry Question 2.
Choose the correct option and justify your choice :
i) \(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}\) =
A) sin 60°
B) cos 60°
C) tan 60°
D) sin 30°
Solution:
A) sin 60°
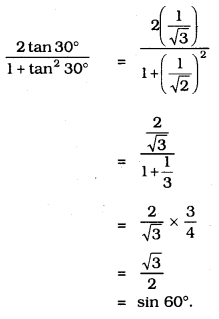
ii) \(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}\) =
A) tan 90°
B) 1
C) sin 45°
D) 0
Solution:
D) 0

iii) sin 2A = 2 sin A is true when A ;
A) 0°
B) 30°
C) 45°
D) 60°
Solution:
A) 0°
LHS = sin 2A = sin 0° = 0
RHS = 2sin A = 2.sin0° = 0
iv) \(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}\) =
A) cos 60°
B) sin 60°
C) tan 60°
D) sin 30°
Solution:
C) tan 60°
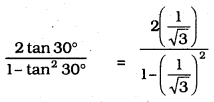
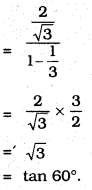
Introduction To Trigonometry Exercise 11.2 Question 3.
If tan (A + B) =\(\sqrt{3}\) and tan (A – B) = \(\frac{1}{\sqrt{3}}\) 0° < A + B ≤ 90°; A > B. find A and B.
Solution:
tan (A + B) = \(\sqrt{3}\)
tan (A + B) = tan 60°
A + B = 60°
tan (A – B) = \(\frac{1}{\sqrt{3}}\) = tan 30°
tan(A – B) = tan 30°
A – B = 30° → (2)
Adding (1) and (2)
A + B + A – B = 60 + 30
2A = 90
A = \(\frac{90}{2}\) = 45°
A = 45°
Put A = 45° in eqn (1)
A + B = 60
B = 60 – A= 60 – 45°
B = 15°.
Introduction To Trigonometry Class 10 Exercise 11.2 Question 4.
State whether the following are true or false. Justify your answer.
i) sin (A + B) = sin A + sin B
Solution:
False
Take A = 45° and B = 45°
LHS: sin (45° + 45°) = sin 90° = 1
RHS: sin 45 + sin 45 = \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}\)
LHS ≠ RHS.
ii) The value of sin θ increases as θ increases.
Solution:
True.
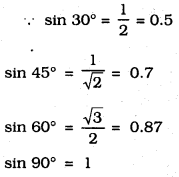
∴ The value of sin θ increases as θ increases.
iii) The value of cos θ increases as θ increases.
Solution:
False.
cos 0° = 1 cos 30° = \(\frac{\sqrt{3}}{2}\) =0.87
cos 45° = \(\frac{1}{\sqrt{2}}\) = 0.7 cos 60° = \(\frac{1}{2}=\) = 0.5
cos 90° = 1
∴ The value of cos 0 increases as 0 increases – the statement is False.
iv) sin θ = cos θ for all values of θ.
Solution:
False.
sin 30° = \(\frac{1}{2}\) cos 30° = \(\frac{\sqrt{3}}{2}\)
sin 30° ≠ cos 30°
But sin 45° = cos 45° = \(\frac{1}{\sqrt{2}}\)
v) cot A is not defined for A = 0°.
Solution:
True.
![]()
∴ When A = 0°, cot A is not defined.
We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Ex 11.2 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.2, drop a comment below and we will get back to you at the earliest.