KSEEB SSLC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.3.
Karnataka SSLC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.3
ex 3.3 class 10 Question 1.
Solve the following pair of linear equations by the substitution method.
(i) x + y = 14
x – y = 14
(ii) s – t = 3
\(\frac{s}{3}+\frac{t}{2}=6\)
(iii) 3x – y = 3
9x – 3y = 9
(iv) 0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
(v) \(\sqrt{2} x+\sqrt{3} y=0\)
\(\sqrt{3} x-\sqrt{8} y=0\)
(vi) \(\frac{3 x}{2}-\frac{5 y}{2}=-2\)
\(\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\)
Solution:
(i) x + y = 14 ………. (i)
x – y = 4 …………. (ii)
In eqn. (i), x + 4 = 14
∴ x = 14 – y
Substituting the value of ‘x’ in equation (ii), we have
x – y = 4
(14 – y) – y = 4
14 – y – y = 4
14- 2y = 4
-2y = 4 – 14
-2y = -10
2y = 10
∴ x = 5
∴ Substituting y = 5 in x = 14 – y,
x = 14 – y
= 14 – 5
x = 9
∴ x = 9, y = 5.
(ii) s – t = 3
\(\frac{s}{3}+\frac{t}{2}=6\)
s – t = 3 …………. (i)
\(\frac{s}{3}+\frac{t}{2}=6\) ………… (ii)
From eqn. (i), s – t = 3
-t = 3 – s
t = -3 + s
Substituting the value of ‘t’ in eqn. (ii),
\(\frac{s}{3}+\frac{-3+s}{2}=6\)
\(\frac{2 s-9+3 s}{6}=6\)
5s – 9 = 6 × 6
5s – 9 = 36
5s = 36 + 9
∴ 5s = 45
∴ s=\(\frac{45}{5}\)
∴ s = 9
Substituting the value of s = 9 in t = -3 + s
t = -3 + s
= -3 + 9
t = 6
∴ s = 9, t = 6
(iii) 3x – y = 3 …………. (i)
9x – 3y = 9 ………… (ii)
From eqn. (i), 3x – y = 3
-y = 3 – 3x
y = – 3 + 3x
Substituting the value of ‘y’ in eqn. (ii),
9x – 3y = 9
9x – 3(-3 + 3x) = 9
9x + 9 – 9x = 9
Here we can give any value for ‘x’ i.e., infinite solutions are there,
y = 3x – 3 Means x = 0 then y = -3
x = 1 then y = 0
x = 2 then y = 3
etc.
(iv) 0.2x + 0.3y = 1.3 …………. (i)
0.4x + 0.5y = 2.3 …………. (ii)
From eqn. (i)„
0.2x + 0.3y = 1.3
0.2x = 1.3 – 0.3y
\(x=\frac{1.3-0.37}{0.2}\)
Substituting the value of ‘x’ in eqn (ii)
0.4x + 0.5y = 2.3
\(0.4\left(\frac{1.3-0.37}{0.2}\right)+0.5 y=2.3\)
0.2 (1.3 – 0.3y) + 0.5y = 2.3
2.6 – 0.6y + 0.5y = 2.3
2.6 – 0.1y = 2.3
-0.1y = 2.3 – 2.6
-0.1y = -0.3
0.1y = 0.3
\(y=\frac{0.3}{0.1}=\frac{3}{1}=3\)
Substituting the vlue of ‘y’ in
\(x=\frac{1.3-0.37}{0.2}\)
\(=\frac{1.3-0.3(3)}{0.2}\)
\(=\frac{1.3-0.9}{0.2}\)
\(=\frac{0.4}{0.2}\)
\(=\frac{4}{2}\)
∴ x = 2
∴ x = 2, y = 3
(v) \(\sqrt{2} x+\sqrt{3} y=0\) ………….. (i)
\(\sqrt{3} x-\sqrt{8} y=0\) ………….. (ii)
From eqn (i)
\(\sqrt{2} x+\sqrt{3} y=0\)
\(\sqrt{2} x=-\sqrt{3} y\)
\(\mathbf{x}=-\frac{\sqrt{3}}{\sqrt{2}} \mathbf{y}\)
Substituting the value of ‘x’ in eqn (ii)

substituting the value of ‘y’ in
\(\mathrm{x}=-\frac{\sqrt{3}}{\sqrt{2}} \mathrm{y}\)
\(=\frac{-\sqrt{3}}{\sqrt{2}} \times 0\)
∴ x = 0
∴ x = 0, y = 0
(vi) \(\frac{3 x}{2}-\frac{5 y}{2}=-2\) ………… (i)
\(\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\) …………….. (ii)
From eqn (ii)
\(\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\)
\(\frac{x}{3}=\frac{13}{6}-\frac{y}{2}\)
\(\frac{x}{3}=\frac{13-3 y}{6}\)
\(x=\frac{3(13-3 y)}{6}\)
\(x=\frac{13-3 y}{2}\)
Substituting the value of ‘x’ in eqn (i)
\(\frac{3 x}{2}-\frac{5 y}{2}=-2\)
\(\frac{3}{2}\left(\frac{13-3 y}{2}\right)-\frac{5 y}{2}=-2\)
\(\frac{39-9 y}{4}-\frac{5 y}{2}=-2\)
\(\frac{39-9 y-10 y}{4}=-2\)
\(\frac{39-19 y}{4}=-2\)
39 – 19y = -2 × 4
39 – 19y = -8
-19y = -8 + 39
-19y = -47
Or 19y = 47
\(y=\frac{47}{19}\)
∴ y = 3
Substituting the value of ‘y’ in
\(x=\frac{13-3 y}{2}\)
\(=\frac{13-3(3)}{2}\)
\(=\frac{13-9}{2}=\frac{4}{2}\)
∴ x = 2
∴ x = 2, y = 3
Question 2.
Solve 2x + 3y = 11 and 2x – 4y = -24 and hence find the value of ‘m’ for which y = mx + c
Solution:
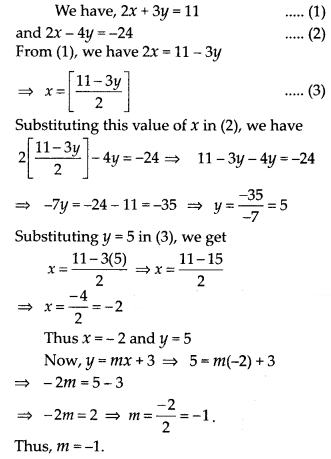
![]()
ex 3.3 class 10 Question 2.
Solve 2x + 3y = 11 and 2x – 4y = -24 and hence find the value of ‘m’ for which y = mx + 3.
Solution:
2x + 3y = 11 …………… (i)
2x – 4y = -24 ………….. (ii)
From eqn. (i),
2x = 3y = 11
2x = 11 – 3y
\(x=\frac{11-3 y}{2}\)
Substituting the value of ‘x’ in eqn. (ii),
2x – 4y = -24
\(2\left(\frac{11-3 y}{2}\right)-4 y=-24\)
11 – 3y – 4y = -24 – 11
-7y = – 35
7y = 35
\(y=\frac{35}{7}\)
∴ y = 5.
Substituting the value of ‘y’ in
\(x=\frac{11-3 y}{2}\)
\(=\frac{11-3(5)}{2}\)
\(=\frac{11-15}{2}\)
\(=\frac{-4}{2}\)
∴ x = -2
∴ x = -2, y = 5
Now, y = mx + 3
5 = m(-2) + 3
5 = -2m + 3
5 – 3 = -2m
-2m = 2
\(\mathrm{m}=\frac{2}{-2}\)
∴ m= -1.
ex 3.3 class 10 Question 3.
Form the pair of linear equations for the following problems and find their solution by substitution method :
(i) The difference between the two numbers is 26 and one number is three times the other. Find them.
Solution:
Let one number be ‘x’.
another number be ‘y’.
Their difference is 26.
∴ x – y = 26 ………. (i)
One number is three times the other,
∴ x = 3y …………. (ii)
Substituting x = 3y in eqn. (i),
x – y = 26
3y – y = 26
2y = 26
\(y=\frac{26}{2}\)
∴ y = 13
Substituting the value of ‘y’ in eqn. (ii),
x = 3y
∴ x = 3 × 13
∴ x = 39, y = 13
(ii) The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
Solution:
In two supplementary angles, let one angle be ‘x’.
another angle be ‘y’
Sum of these = 180°
∴ x + y = 180 ………… (i)
The larger of two supplementary angles exceeds the smaller by 18 degrees.
∴ x-y = 18 ………… (ii)
From eqn. (ii),
x – y = 18
x = 18 + y
Substituting the value of ‘x’ in eqn. (i),
x + y = 180 .
18 +y + y = 180
18 + 2y = 180
2y = 180 – 18
2y = 162
\(\mathrm{y}=\frac{162}{2}\)
∴ y = 81
Substituting the value of y’ in x = 18 + y
x = 18 + 81
x = 99
∴ x = 99°, y = 81°.
![]()
(iii) The coach of a cricket team buys 7 bats and 6 balls for Rs. 3800. Later, she buys 3 bats and 5 balls for Rs. 1750. Find the cost of each bat and each ball.
Solution:
Let the cost of each bat b Rs. x.
Let the Cost of each ball be Rs. y.
∴ 7x + 6y = 3800
3x + 5y= 1750
From eqn. (ii),
3x + 5y = 1750
3x = 1750 – 5y
\(x=\frac{1750-5 y}{3}\)
Substituting the value of ‘x’ in eqn. (i),
\(7\left(\frac{1750-5 y}{3}\right)+6 y=3800\)
\(\frac{12250-35 y}{3}+\frac{6 y}{1}=3800\)
\(\frac{12250-35 y+18 y}{3}=3800\)
12250 – 17y = 3800 × 3
12250 – 17y = 11400
-17y = 11400 – 12250
-17y = -850
\(y=\frac{850}{17}\)
∴ y = Rs. 50
Substituting the value of ‘y’ in
\(x=\frac{1750-5 y}{3}\)
\(=\frac{1750-5 \times 50}{3}\)
\(=\frac{1750-250}{3}\)
\(=\frac{1500}{3}\)
∴ x = Rs. 500
∴ x = Rs. 500, Rs. y = 50
∴ Cost of each bat is Rs. 500,
Cost of each ball is Rs. 50.
(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is Rs. 105 and for a journey of 15 km, the charge paid is Rs. 155. What are the fixed charges and the charge per km? How much does a person have to pay for travelling a distance of 25 km?
Solution:
Let the fixed charge of the taxi be Rs. x.
If the charge for each km is Rs. y, then
Fixed charge + Charge for 10 km
= Rs. 105
∴ x + 10y = 105 ………. (i)
Fixed charge + Charge for 15 km travelled
= Rs. 155
∴ x + 15y = 155 ……….. (ii)
From eqn. (i),
x + 10 y = 105
x = 105 – 10y
Substituting the value of ’x’ in eqn. (ii),
x + 15y = 155
105 – 10y + 15y = 155
105 + 5y = 155
5y = 155 – 105
5y = 50
∴ \( \mathrm{y}=\frac{50}{5}\)
∴ Rs. y = 10.
Substituting the value of y in
x = 105 – 10y,
= 105 – 10 × 10
= 105 – 100
∴ x = Rs. 5
∴ Fixed Charge of Taxi is Rs. 5.
Charge for each km is Rs. 10
Charge for 1 km is Rs. 10
Charge for 25 km = 25 × 10 = Rs. 250.
(v) A fraction becomes \(\frac{9}{11}\). if 2 is added to both the numerator and the denominator. If 3 is added to both the numerator and the denominator it becomes \(\frac{5}{6}\). Find the fraction.
Solution:
If the Numerator is ‘x’ and denominator is ‘y’, then the Fraction is \(\frac{x}{y}\).
Adding 2 to both Numerator and denominator, then fraction is \(\frac{9}{11}\).
\(\frac{x+2}{y+2}=\frac{9}{11}\)
11 (x + 2) = 9(y + 2)
11x + 22 = 9y + 18
11x – 9y + 22 – 18 = 0
11x – 96 + 4 = 0 ……….. (i)
If 3 is added to both Numerator and denominator, then the fraction is \(\frac{5}{6}\).
\(\frac{x+3}{y+3}=\frac{5}{6}\)
6(x + 3) = 5 (y + 3)
6x + 18 = 5y + 15
6x – 5y + 18 – 15 = 0
6x – 5y + 3 = 0 ………… (ii)
From eqn. (i),
11x – 9y + 4 = 0
11x = 9y – 4
\(x=\frac{9 y-4}{11}\)
Substituting the value of ‘x’ in eqn. (ii),
6x – 5y + 3 = 0
\(6\left(\frac{9 y-4}{11}\right)-5 y+3=0\)
\(\frac{54 y-24}{11}-\frac{5 y}{1}+\frac{3}{1}=0\)
\(\frac{54 y-24-55 y+33}{11}=0\)
-y + 9 = 0
-y = -9
∴ y = 9
Substituting the value of ‘y’ in
\(x=\frac{9 y-4}{11}\)
\(=\frac{9 \times 9-4}{11}\)
\(=\frac{81-4}{11}\)
\(=\frac{77}{11}\)
∴ x = 7.
∴ Fraction is \(\frac{x}{y}=\frac{7}{9}\)
![]()
(vi) Let the present age of Jacob = x years
and the present age of his son = y years
∴ 5 years hence: Age of Jacob = (x + 5) years
Age of his son = (y + 5) years
According to given condition,
[Age of Jacob] = 3[Age of his son]
x + 5 = 3(y + 5) ⇒ x + 5 = 3y + 15
⇒ x – 3y -10 = 0 … (1)
5years ago : Age of Jacob = (x – 5) years,
Age of his son = (y – 5) years
According to given condition,
[Age of Jacob] = 7[Age of his son]
∴ (x – 5) = 7(y – 5) ⇒ x – 5 = 7y – 35
⇒ x – 7y + 30 = 0 … (2)
From (1) , x = [10 + 3y] … (3)
Substituting this value of x in (2) , we get
(10 + 3y) – 7y + 30 = 0
⇒ -4y = -40 ⇒ y = 10
Now, substituting y = 10 in (3) ,
we get x = 10 + 3(10)
⇒ x = 10 + 30 = 40
Thus, x = 40 and y = 10
⇒ Present age of Jacob = 40 years and present age of his son = 10 years
We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.3, drop a comment below and we will get back to you at the earliest