You can Download Chapter 5 Laws of Motion Questions and Answers, Notes, 1st PUC Physics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 1st PUC Physics Question Bank Chapter 5 Laws of Motion
1st PUC Physics Laws of Motion TextBook Questions and Answers
Question 1.
Give the magnitude and direction of the net force acting on
- a drop of rain falling down at a constant speed.
- a cork of mass 10 g floating on water
- a kite skillfully held stationary in the sky.
- a car moving with a constant velocity of 30 km/h on a rough road.
- a high-speed electron in space far from ail material objects, and free of electric and magnetic fields.
Answer:
- In accordance with the first law of motion, there is no net force on the drop since it is moving with constant speed.
- The weight of the cork is balanced by upthrust which is equal to the weight of water displaced. Hence no net force on the cork.
- Since the kite is in the state of rest net force on it is zero.
- From the first law of motion, since the velocity of the car is a constant net force on it is zero.
- Since the electron is in free space no gravitational or electric or magnetic force is acting on it. Hence net force on it is zero.
Question 2.
A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble,
- during its upward motion.
- during its downward motion.
- at the highest point where it is momentarily at rest. Do your answers change if the pebble was thrown at an angle of 45° with the horizontal direction? Ignore air resistance.
Answer:
- When the pebble is moving upward the force acting on it is gravitational force in downward direction. F = mg = 0.05 × 10 = 0.5 N
- Even in this case F = mg = 0.5 N in downward direction.
- Since there is no force other than gravitational force acting on pebble, during the whole process F = mg = 0.5 N. Note that pebble moves in opposite direction because of its initial velocity. The situation remains same for pebble thrown at an angle.
Question 3.
Give the magnitude and direction of the net force acting on a stone of mass 0.1 kg,
- Just after it is dropped from the window of a stationary train.
- Just after It is dropped from the window of a train running at a constant velocity of 36 km/h
- Just after it is dropped from the window of a train accelerating with 1 ms-2
- Lying on the floor of a train which is accelerating with 1 m s-2, the stone being at rest relative to the train. Neglect air resistance throughout.
Answer:
- Gravitational force is acting on the stone in downward direction F = mg = 0.1 × 10 = 1 N
- Once the stone is dropped from the train, the only force acting on it is gravitation force =1 N.
- Since there is no contact between train and stone the force acting on it is again gravitational force.
- Since the stone is lying on the floor of train its acceleration in the same as that of the train. Hence the force excreted by train on the stone is F = ma = 0.1 × 1 = 0. 1 N in the direction of the train. The weight is balanced by the normal reaction of the floor of the train.
Question 4.
One end of a string of length L is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v the net force on the particle (directed towards the centre) is:
- T.
- T – \(\frac{m v^{2}}{L}\)
- T + \(\frac{m v^{2}}{L}\)
- 0
T is the tension in the string. [Choose the correct alternative].
Answer:
1. The centripetal force necessary for the particle to move in a circular path is provided by the tension in the string. Hence net force on the particle is nothing but tension T in the string.
![]()
Question 5.
A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 ms-1. How long does the body take to stop?
Answer:
Given F = – 50 N (retarding force)
m = 20 kg
u = 15 m/s. V = 0 m/s
t = ?
F = ma ⇒ a = \(\frac{\mathrm{F}}{\mathrm{m}}\) = \(\frac{-50}{20}\) = – 2.5m/s2
but we know that
V = u + at
0 = 15 + (- 2.5) t
⇒ t = 6 s.
Question 6.
A constant force acting on a body of mass 3.0 kg changes its speed from 2.0 m s-1 to 3.5 m s-1 in 25 s. The direction of the motion of the body remains unchanged. What is the magnitude and direction of the force?
Answer:
Given m = 3 kg
u = 2 m/s
v = 3.5 m/s
t = 25 s.
F = ma
but we know that a = \(\frac{v-u}{t}\)
∴ F = m \(\left(\frac{v-u}{t}\right)\) = 3 \(\left(\frac{3.5-2}{25}\right)\)
= 0.18 N
since direction acceleration ‘a’ is positive force is acting in the direction of motion.
Question 7.
A body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N. Give the magnitude and direction of the acceleration of the body.
Answer:
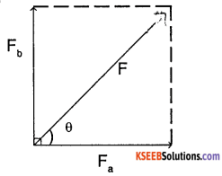
Given Fa = 8 N
Fb = 6 N
m = 5 kg
The result ant force F is given by,
F = \(\sqrt{\mathrm{Fa}^{2}+\mathrm{Fb}^{2}}\)
= \(\sqrt{64+36}\) = 10 N
we know from the figure that
tan θ = \(\frac{F_{b}}{F_{a}}=\frac{6}{8}\) = 0.75
⇒ θ = tan-1(0.75) = 37° with 8 N force
Question 8.
The driver of a three wheeler moving with a speed of 36 km/h sees a child standing in the middle of the road and brings his vehicle to rest in 4.0 s just in time to save the child. What is the average retarding force on the vehicle? The mass of the three- wheeler is 400 kg and the mass of the driver is 65 kg.
Answer:
Given, u = 36 km/h
36 × \(\frac{1000}{3600}\) m/s
=10 m/s
v = 0
t = 4 s
m = 400 + 65 = 465 kg
a = \(\frac{v-u}{t}\) = \(\frac{-10}{4}\) = – 2.5 m/s²
F = ma = 465 (- 2. 5)
= – 11625 N (retarding force)
Question 9.
A rocket with a lift-off mass 20,000 kg is blasted upwards with an initial acceleration of 5.0 ms-2. Calculate the initial thrust (force) of the blast.
Answer:
Given m = 20000 kg
a = 5ms-2 (against gravity) since the rocket has to move upwards against gravity the total initial thrust of the blast is given by
F = ma + mg
= m (a + g) = 20000 (5 + 9.8)
= 296 × 105 N.
Question 10.
A body of mass 0.40 kg moving initially with a constant speed of 10 m s-1 to the north is subject to a constant force of 8.0 N directed towards the south for 30 s. Take the instant the force is applied to be t= 0, the position of the body at that time to be x= 0, and predict its position at t = – 5 s, 25 s, 100 s.
Answer:
Given mass m = 0.4 kg
Retarding force F = – 8 N
∴ acceleration a = \(\frac{F}{m}\) = \(\frac{-8}{0.4}\) = – 20 m/s²
at t = – 5 s
a = 0 for t < 0
∴ s = u + \(\frac{1}{2}\) at²
= 10 (-5) + \(\frac{1}{2}\) (0)(-5)²
at t = 25 s
S = ut+\(\frac{1}{2}\) at²
= 10 (25) + \(\frac{1}{2}\) (- 20) (25)²
= – 6000 m
at t = 100 s
since there is a retarding force for 30 s
S1 = ut + \(\frac{1}{2}\) at²
= 10 (30) + \(\frac{1}{2}\) (-20) (30)²
= – 8700 m .
after 30 s it move with a constant velocity.
V = u + at
= 10 – 20 (30)
= – 590 m/s
for rest of 70 s.
S2 = – 590 (70) + \(\frac{1}{2}\) (0) (70)² = -41300 m
∴ Total distance = S1 + S2 = 50000 m.
![]()
Question 11.
A truck starts from rest and accelerates uniformly at 2.0 m s-2. At t = 10 s, a stone is dropped by a person standing on the top of the truck (6 m high from the ground). What are the
- velocity, and
- acceleration of the stone at t = 11s? (Neglect air resistance.)
Answer:
We have, Vt = u + at
i.e. Vt = 0 + 2 (10) = 20 ms-1
During the nextone second stone is under the effect of gravity.
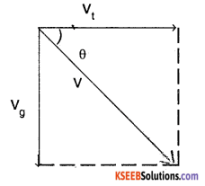
Vg = u + gt
= 0 + 9.8 (1) = 9.8 m/s
∴ Net velocity of stone at t = 11 s
v = \(\sqrt{V_{t}^{2}+V_{g}^{2}}\) = 22.27 m/s.
tan θ = \(\frac{V_{g}}{V_{t}}=\frac{9.8}{20}\)
⇒ θ = 26.1° with horizontal.
(b) The moment stone is dropped from truck only gravitational force is acting on it.
∴ acceleration = g = 9.8 m/s².
Question 12.
A bob of mass 0.1 kg hung from the celling of a room by a string 2 m long is set into oscillation. The speed of the bob at its mean position is 1 m s-1. What is the trajectory of the bob if the string is cut when the bob is
- at one of its extreme positions
- at its mean position.
Answer:
1. When the bob is at one of its extreme positions its velocity is zero. Hence if the string is cut, it will fall straight down due to gravitational force.
2. At the mean position the bob has a horizontal velocity of 1 m/s. If the string is cut, bob is acted by vertical gravitational force = a = 9.8 ms-2. Hence bob will behave like a projectile and follows a parabolic path.
Question 13.
A man of mass 70 kg stands on a weighing scale in a lift which is moving
- upwards with a uniform speed of 10 m s-1
- downwards with a uniform acceleration of 5 m s-2
- upwards with a uniform acceleration of 5 ms-2. What would be the readings on the scale in each case?
- What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?
Answer:
The weighing machine measures the reaction R which is nothing but the apparent weight.
1. when the lift is moving upwards with uniform speed.
R = mg = 70 × 9.8 = 686 N.
2. When lift moves downwards with an acceleration of 5m/s²
R = m (g – a) = 70 (9.8 – 5) = 336 N.
3. When lift moves upwards with with an acceleration of 5m/s²
R = m (g + a) = 70 (9.8 + 5) = 1036 N.
4. If the lift falls down freely under gravity
R = m (g – g) = 0.
Question 14.
Figure shows the position-time graph of a particle of mass 4 kg. What is the
- force on the particle for t < 0, t > 4 s, 0 < t < 4 s?
- impulse at t = 0 and t = 4 s? (Consider onedimensional motion only)
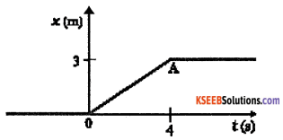
Answer:
1. From the position time graph we can see that the particle is in rest during t < 0 and t > 4. Hence net force on it is zero t < 0, t > 4 s. During 0 < t < 4; the graph has a constant slope i.e, particle
has uniform velocity = 3/4 = 0.75 m/s.
Hence net force is zero.
2. at t = 0 u = 0 v = 0.75
impulse = change in momentum
= M (v – u) = 4 (0.75 – 0)
= 3 kg m/s
at t = 4, u = 0.75 v = 0
impulse = 4 (0 – 0.75) = – 3 kg m/s.
Question 15.
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string, a horizontal force F = 600 N is applied to
- A
- B along the direction of string. What is the tension in the string in each case?
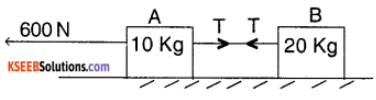
Answer:
1. Acceleration of the whole system a = \(\frac{F}{M_{1}+M_{2}}=\frac{600}{10+20}\) = 20ms-2
The net force, acting on A
= 600 – T = m1 (a)
∴ 600 – T = 10 × 20
⇒ T = 400 N.
2. similar to the above case.
The net force acting on B
= 600 – T = M2 a
∴ 600 – T = 20 × 20
⇒ T = 200 N.
![]()
Question 16.
Two masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley. Find the acceleration of the masses, and the tension in the string when the masses are released.
Answer:
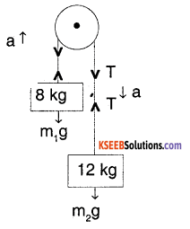
Let ‘a’ be the acceleration of the masses. Then
for block m1, T – m1g = m1a → (1)
for block m2, m2g – T = m2 a → (2)
(1) + (2) (m2 – m1) g = (m1 + m2) a
⇒ a = \(\frac{12-8}{12+8}\) g = 2m/s
substituting in (1)
T – 8 × 10 = 8 × 2
⇒ T = 96 N
Question 17.
A nucleus is at rest in the laboratory frame of reference. Show that if it disintegrates into two smaller nuclei the products must move in opposite directions.
Answer:
Let m1 & m2 be the masses of smaller nuclei and let \(\vec{v}_{1}\) & \(\vec{v}_{2}\) be their velocities.
According to the law of conservation of momentum.
Initial momentum = final momentum
0 = m1\(\vec{v}_{1}\) + \(\vec{v}_{2}\)
Or \(\vec{v}_{2}\) = – \(-\frac{m_{1}}{m_{2}} \vec{v}_{1}\)
Hence v1 & v2 are in opposite direction.
Question 18.
Two billiard balls each of mass 0.05 kg moving in opposite directions with speed 6 m s-1 collide and rebound at the same speed. What is the impulse imparted to each bail due to the other?
Answer:
Impulse = change in momentum
Initial momentum of each ball = 0.05 × 6
= 0.3 kg m/s
Final momentum of each ball = 0.05 × (-6)
= – 0.3 kg m/s
Impulse = 0.6 kgm/s (in magnitude).
Question 19.
A shell of mass 0.020 kg is fired by a gun of mass 100 kg. If the muzzle speed of the shell is 80 m s-1, what is the recoil speed of the gun?
Answer:
Given
m1 = 0.02 kg, m2 = 100 kg
v1 = 80 m/s v2 = ?
According law of conservation of momentum
m1u1 + m2u2 = m1v1 + m2v2
0.02 (0) + 100 (0) = 0.02 × 80 + 100 × v2
v2 = – 1.6 × 10-2 m/s
Question 20.
A batsman deflects a ball by an angle of 45° without changing its initial speed which is equal to 54 km/h. What is the impulse imparted to the ball? (Mass of the ball is 0.15 kg.)
Answer:
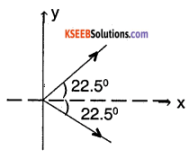
given
m = 0.15 kg
u = 54 kmph
= 54 × \(\frac{1000}{3600}\)
= 15m/s
Along x -axis
Initial velocity = – u cos θ
= 15 cos (22.5°)
Final velocity = u cos θ
= 15 cos (22.5°)
∴ Impulse = change in momentum
= 0.15 [15 cos (22.5) – (-15 cos (22.5)°)]
= 4.16 kgm/s.
Along y-axis
Initial velocity = Final velocity = – u sin θ
∴ No impulse along the y-axis.
Question 21.
A stone of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40 rev/min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
Answer:
Given m = 1.5m
r = 1.5 m
w = 40 rpm = \(40 \frac{\times 2 \pi}{60}\) rad/s
= \(\frac{4}{3}\)π rad/s
Now Tension T = mrw²
= 0.25 × 1.5 × \(\left(\frac{4}{3} \pi\right)^{2}\)
= 0.58 N
Tmax = 200 N
Tmax = \(\frac{\mathrm{m} \mathrm{v}_{(\mathrm{max})}^{2}}{\mathrm{r}}\)
⇒ Vmax = \(\sqrt{\frac{200 \times 1.5}{0.25}}\) = 34.6 m/s.
Question 22.
If, In Exercise 5.21, the speed of the stone is increased beyond the maximum permissible value, and the string breaks suddenly, which of the following correctly describes the trajectory of the stone after the string breaks:
- the stone moves radially outwards,
- the stone flies off tangentially from the instant the string breaks,
- the stone flies off at an angle with the tangent whose magnitude depends on the speed of the particle?
Answer:
The answer is 2. When a particle moves in a circular path, at each point the velocity is directed along the tangent of the circular path. Hence when string, breaks, it moves along the tangent in accordance with Newton’s 1st law of motion.
Question 23.
Explain why
- a horse cannot pull a cart and run in empty space.
- passengers are thrown forward from their seats when a speeding bus stops suddenly.
- it is easier to pull a lawnmower than to push it.
- a cricketer moves his hands backward while holding a catch.
Answer:
- In accordance with Newton’s 1st law of motion since there is no external agent the horse cannot pull cart.
- The passenger continues to move forward when a speeding bus breaks because of their inertia of motion. Hence they are thrown forward from their seats.
- A lawn mover is pulled or pushed by applying a force at an angle. When it is pushed, the normal force (N) must be more than its weight, for equilibrium in the vertical direction. This results in greater friction and hence greater applied force to move. It is just opposite while pulling.
- The ball will have a large momentum. If the player tries to stop it instantaneous, the time of contact is low which results in a large impulse which may hurt his hand. Hence he tries to move his hands backward which increases the time of contact hence reducing the impulse.
1st PUC Physics Laws of Motion Additional Exercises Questions and Answers
Question 24.
The figure shows the position-time graph of a body of mass 0.04 kg. Suggest a suitable physical context for this motion. What is the time between two consecutive impulses received by the body? What is the magnitude of each impulse?
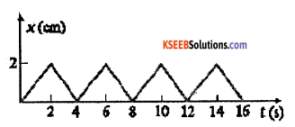
Answer:
The graph could be representing a ball rebounding between two walls separated by 2 cm with a constant velocity in free space. After receiving the impulse ball changes its direction. Hence time between two impulses is 2 seconds.
velocity = \(\frac{\text { displacement }}{\text { time }}\) = \(\frac{2 \times 10^{-2}}{2}\) = 0.01m/s
Initial momentum,
mu = 0.04 × 10-2kgm/s
Final momentum,
mv = – 0.04 × 10-2kgm/s
∴ Change in momentum = 0.08 × 10-2kgm/s
Question 25.
Figure 5.18 shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with 1 m s-2. What is the net force on the man? If the coefficient of static friction between the man’s shoes and the belt is 0.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt?
(Mass of the man = 65 kg.)
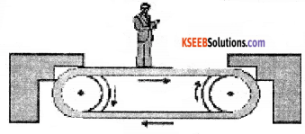
Answer:
Given acceleration of conveyor belt a = 1 m s-2
µs = 0.2
mass of man m = 65 kg
Then man experiences a pseudo force Fs = ma as he is in an accelerating frame as shown in the figure. Hence to maintain his equilibrium he exerts a force F = – Fs = ma = 65 × 1 = 65 N in direction of motion of belt.
∴ Net force acting on man = 65 N The man continue to be stationary with respect to belt if force of friction equal to force acting on man i.e.
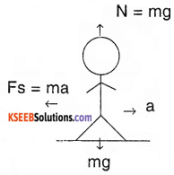
µs N = mamax
µs . m .g = mamax
a(max) = µs × g
= 0.2 × 10
= 2m s-2
Question 26.
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are : [Choose the correct alternative]

T1 and v1 denote the tension and speed at the lowest point. T2 and v2 denote corresponding values at the highest point.
Answer:
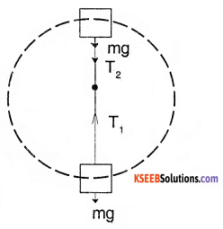
The net force acting on stone at the lowest point directed vertically downward = mg – T1 & and the highest point = mg + T2. Hence option (a) is correct answer.
Question 27.
A helicopter of mass 1000 kg rises with a vertical acceleration of 15 ms-2. The crew and the passengers weigh 300 kg. Give the magnitude and direction of the
- force on the floor by the crew and passengers,
- action of the rotor of the helicopter on the surrounding air,
- force on the helicopter due to the surrounding air.
Answer:
mass of helicopter = mh = 1000 kg mass of crew = mc = 300 kg
vertical acceleration, a =15 m/s².
1. force on the floor by crew & passenger = apparent weight of crew & passenger
= mc (g + a)
= 300(10 + 15)
= 7500 N.
2. The action of motor of helicopter on surrounding air is vertical downwards. The helicopter rises on account of reaction to this force
= (mn + mc) (g + a)
= (1000 + 300) (10 + 15)
= 32500 N.
3. force on helicopter due to the surrounding air is nothing but the reaction to the action of rolor = 32500 N in vertically upward direction.
![]()
Question 28.
A stream of water flowing horizontally with a speed of 15 m s-1 gushes out of a tube of cross-sectional area 10-2 m² and hits a vertical wall nearby. What is the force exerted on the wall by the Impact of water, assuming It does not rebound?
Answer:
The volume of water hitting the wall per second
= (Area × Velocity) of a stream of water
= 10-2 × 15
= 0.15 m3s-1
density of water = 1000 kg/m3
∴ mass of water hitting the wall per second
= 0.15 × 1000= 150 kg/s
Initial momentum of water hitting the wall per second
= 150 × 15
= 250 kg m/s² or 2250 N
Final momentum per second = 0
∴ Force exerted on the wall: change in momentum per second
= 2250 N.
Question 29.
Ten one-rupee coins are put on top of each other on a table. Each coin has a mass m. Give the magnitude and direction of
- the force on the 7th coin (counted from the bottom) due to all the coins on its top,
- the force on the 7th coin by the 8th coin,
- the reaction of the 6th coin on the 7th coin.
Answer:
1. There are 3 coins above the 7th coin
Hence force = (3m) g
= 3mg N
2. The 8th coin has two coins above it. Hence force exerted by 8th coin on 7th is, it’s weight plus the weight of two coins
= mg + 2 mg
= 3 mg N.
3. The 6th coin is under the weight of 4 coins above it
Reaction R = – F = – 4 mg N.
Question 30.
An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at 15°. What is the radius of the loop?
Answer:
υ = 720 km/hr = 720 × \(\frac{1000}{3600}\)
= 200 m/s
θ = 15°
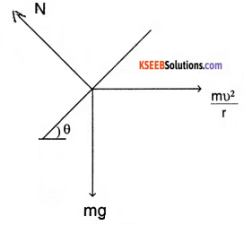
From the relation
tan θ = \(\frac{v^{2}}{r g}\)
⇒ r = \(\frac{v^{2}}{\tan \theta \times g}\) = \(\frac{200 \times 200}{\tan 15^{\circ} \times 10}\)
= \(\frac{200 \times 200}{0.2679 \times 10}\)
= 14931 m
Question 31.
A train runs along an unbanked circular track of radius 30 m at a speed of 54 km/h. The mass of the train is 106 kg. What provides the centripetal force required for this purpose The engine or the rails? What is the angle of banking required to prevent wearing out of the rail?
Answer:
radius r = 30 m
velocity υ = 54 km/h = 54 × \(\frac{1000}{3600}\)= 15 m/s
mass m = 106 kg
The centripetal force F = \(\frac{m v^{2}}{r}\) is provided by the lateral frictional force between rails and wheels of train.
The angle of banking required to prevent the wearing out of rail
tan θ = \(\frac{v^{2}}{r g}\) = \(\frac{15 \times 15}{30 \times 10}\) = 0.75
θ = tan-1 (0.75) ≈ 37°.
![]()
Question 32.
A block of mass 25 kg is raised by a 50 kg man in two different ways as shown in Fig. What is the action on the floor by the man in the two cases? If the floor yields to a normal force of 700 N, which mode should the man adopt to lift the block without the floor yielding?
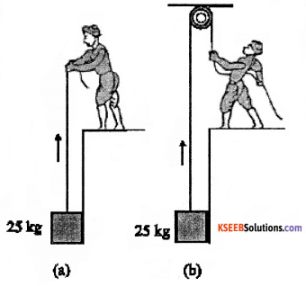
Answer:
In the first case man applies an upward force of 25 kg weight. Hence the action on the floor by man is
= 50 kg weight + 25 kg weight = 75 kg weight
= 75 × 10
= 750 N.
In the second case man applies a downward force of 25 kg weight. Hence the action on the floor by man is
= 50 kg weight – 25 kg weight = 25 × 10
= 250 N.
(other 500 N is applied on the ceiling) Hence man should adopt the second case.
Question 33.
A monkey of mass 40 kg climbs on a rope (Fig.) which can stand a maximum tension of 600 N. In which of the following cases will the rope break: the monkey
- climbs up with an acceleration of 6 m s-2
- climbs down with an acceleration of 4 m s-2
- climbs up with a uniform speed of 5 m s-1
- falls down the rope nearly freely under gravity? (Ignore the mass of the rope).

Answer:
1. When monkey climbs up with an acceleration ‘a’ then
T – mg = ma
Or T = m (g + a)
= 40 (10 + 6)
= 640 N
which exceeds the maximum tension which rope can withstand (600 N), hence rope breaks.
2. when monkey is climbing down with an acceleration a
mg – T = ma
or T = m (g – a)
= 40 (10-4)
= 240 N
The rope will not break.
3. when the monkey climbs up with uniform speed then
T = mg
= 40 × 10
= 400 N
The rope will not break.
4. when the monkey is falling freely, it would be a state of weightlessness. So, there won’t be any tension in the rope hence it will not break.
Question 34.
Two bodies A and B of masses 5 kg and 10 kg in contact with each other rest on a table against a rigid wail (Fig). The coefficient of friction between the bodies and the table is 0.15. A force of 200 N is applied horizontally to A. What are
- the reaction of the partition
- the action-reaction forces between A and B?
- What happens when the wall is removed? Does the answer to (b) change, when the bodies are in motion? ignore the difference between µs and µk.
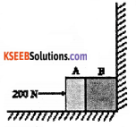
Answer:
1. As the blocks are at rest against the rigid walls, reaction of the partition = – (force applied on A)
= 200 N towards left.
2. The action-reaction force between A & B are 200 N each.
3. when the wall is removed, the pushing force gives acceleration to the system. On taking the coefficient of friction into account,
200 – µ (m1 + m2) g = (m1 + m2) a
a = \(\frac{200-0.15(5+10) \times 10}{(5+10)}\)
= 11.8 ms-2
Let the force exerted by A on B be FBA. On considering the equilibrium of the only block
A, 200 – fk1 = m1 a + FBA
FBA = 200 – µ m1 g – m1 a
= 200 – 7.5 – 59
= 133.5 N towards left.
Question 35.
A block of mass 15 kg is placed on a long trolley. The coefficient of static friction between the block and the trolley is 0.18. The trolley accelerates from rest with 0.5 m s-2 for 20 s and then moves with uniform velocity. Discuss the motion of the block as
viewed by
- a stationary observer on the ground,
- an observer moving with the trolley.
Answer:
1. Force experienced by block
F = ma = 15 × 0.5 = 7.5 N
Force of friction, Ff = µ mg = 0.18 × 15 × 10 = 27 N
Since the force experienced block is less than frictional force it wilt remain stationary with respect to trolley. For an observer on the ground block appears to move with same acceleration as trolley,
2. For an observer moving with trolley the block appears to he stationary as there is no relative motion between him and trolley and the block.
Question 36.
The rear side of a truck is open and a box of 40 kg mass is placed 5 m away from the open end as shown in Fig. The coefficient of friction between the box and the surface below it is 0.15. On a straight road, the truck starts from rest and accelerates with 2 m s-2. At what distance from the starting point does the box fail off the truck? (ignore the size of the box).
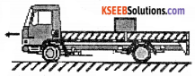
Answer:
Force experienced by box F = ma = 40 × 2 = 80 N
frictional force Ffriction= µ mg = 0.15 × 40 × 10 = 60 N
∴ Net force on the box = F – Ffriction = 80 – 60 = 20 N .
∴ The backward acceleration experienced by box is given by,
a = \(\frac{\text { Net force }}{\text { mass }}\) = \(\frac{20}{40}\) = 0.5 m/s²
Let‘t’ be the time taken by box to move through 5m backwards
We have, S = ut + \(\frac{1}{2}\) at²
∴ 5 = 0 × t + \(\frac{1}{2}\) × 0.5 × t²
t = \(\sqrt{20} \approx\) 4.47 s
The distance travelled by truck in t = 4.47s is
s = ut + \(\frac{1}{2}\) at² (a = 2m /s2)
s = 0 × \((\sqrt{20})\) + \(\frac{1}{2}\) × 2 \((\sqrt{20})^{2}\)
s = 20 m
The box will off the truck after 20 m from starting point.
Question 37.
A disc revolves with a speed of \(33 \frac{1}{3}\) rev/min, and has a radius of 15 cm. Two coins are placed at 4 cm and 14 cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.15, which of the coins will revolve with the record?
Answer:
If the coin is to revolve with the record then the force of friction must be enough to provide the necessary centripetal force.
i.e. mr ω² ≤ µs mg or r ≤ \(\frac{\mu_{\mathrm{s}} \mathrm{g}}{\omega^{2}}\)
Here, ω = \(33 \frac{1}{3}\) rpm

\(\approx\) 0.12 m
The coin placed within the radial distance of 0.12 m will revolve with the record. Hence coin at 4 cm will revolve with the record.
Question 38.
You may have seen in a circus a motorcyclist driving in vertical loops Inside a ‘deathwell’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
Answer:
When the motor cyclist is at the highest point of death well, the normal readction R on the motor cycle by the ceiling of the chamber acts downwards. His weight mg also acts downwards. These two forces are balanced by the outward centrifugal acting on him.
∴ R + mg = \(\frac{m v^{2}}{r}\) → (1)
The minimum speed required to perform vertical loop is given by equation (1) when
R = 0
∴ mg = \(\frac{m v^{2}_{(\min )}}{r}\)
υmin = \(\sqrt{\mathrm{rg}}\) = \(\sqrt{25 \times 10}\)
≈ 15.8 m/s.
![]()
Question 39.
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/mln. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
Answer:
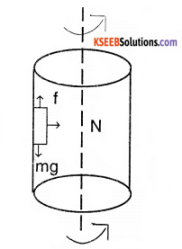
The horizontal force N exerted by the wall on the man provides the necessary centrepetal force.
∴ N = m ω² r
The static frictional force (vertically upwards) balances the weight of the man mg.
The man remains stuck to the wall after the floor is removed if mg 〈 µ N
i.e., mg 〈 µ mRω²
∴ Minimum angular speed of rotation is
⇒ ωmin = \(\sqrt{\frac{g}{\mu_{s}} r}\) = \(\sqrt{\frac{10}{0.15 \times 3}}\) = 4.6 rad/s
Thus the minimum rotational speed of cylinder required to hold the man stuck to the wall is 4.6 rad/s
Question 40.
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω
- Show that a small bead on the wire loop remains at its lowermost point for ω ≤ \(\sqrt{g / R}\)
- What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω = \(\sqrt{2 \mathrm{g} / \mathrm{R}}\)? Neglect friction.
Answer:
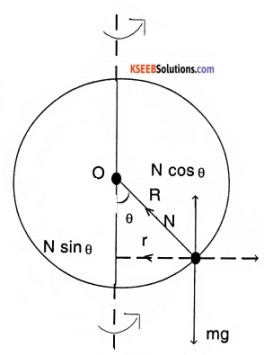
1. Let the radius vector joining the bead to the center of the wire make an angle θ with vertical downward direction. Let N be the normal reaction. From fig,
mg = N cos θ → (1)
mr ω² = N sin θ → (2)
or m (R sin θ ) ω² = N sin θ
mRω² = N
On substituting in (1)
mg = (m Rω²) cos θ
0r ω = \(\sqrt{\frac{9}{\mathrm{R} \cos \theta}}\)
For the bead to remain in lower most position θ = 0
⇒ cos θ = 1
⇒ ω ≤ \(\sqrt{\frac{\mathrm{g}}{\mathrm{R}}}\)
2. when ω = \(\sqrt{\frac{2 g}{R}}\)
cos θ = \(\sqrt{\frac{g}{R \omega^{2}}}\) = \(\frac{g}{R\left(\frac{2 g}{R}\right)}\)
⇒ θ =60°
∴ apparent weight = m (g – a).
1st PUC Physics Laws of Motion One Mark Questions and Answers
Question 1.
Define force.
Answer:
Force is defined as that external agent acting on a body changes its state of rest or uniform motion along a straight line.
Question 2.
Define inertia.
Answer:
The tendency of a body to oppose any change in its state of rest or of uniform motion is called inertia.
Question 3.
State Newton’s first law of motion (or Law of inertia).
Answer:
Everybody continues to be in its state of rest or uniform motion along a straight line unless compelled to change that state by an external force.
Question 4.
Define Linear momentum.
Answer:
The momentum of a body to defined to be the product of mass and velocity and is denoted by P \(\overrightarrow{\mathrm{P}}\) = \(m \bar{v}\)
Question 5.
State Newton’s Second law of motion.
Answer:
The rate of change of momentum of the body is directly proportional to the applied force and takes place in the direction of the force.
Question 6.
Define newton.
Answer:
One newton is defined as that force which acting on a body of mass 1kg produces an acceleration of 1 m/s2
Question 7.
Give the dominion formula for
a)Force
b) momentum
Answer:
Force – MLT-2
Momentum – MLT-1
![]()
Question 8.
What quantity is conserved during rocket propulsion?
Answer:
Linear Momentum.
Question 9.
Action and reaction forces do not cancel each other. Why?
Answer:
Action and reaction forces do not cancel each other because they act on different objects.
Question 10.
What is the apparent weight measured? When a person of mass ‘m’ is standing in a lift accelerating with an acceleration of ‘a’
(i) Downwards
Answer:
The weighting machine measures the reaction force given by the floor. So when lift is going
i) downwards the weight measured is lesser
Question 11.
ii) Upwards
Answer:
ii) Upwards the weight measured is more
∴ apparent weight = m (g + a)
Question 12.
State Newton’s third law of motion.
Answer:
For every action, there is an equal and opposite reaction.
Question 13.
Which is the weakest force in nature?
Answer:
Gravitational force.
Question 14.
Is it possible for the weight of a body to be zero?
Answer:
Yes, whenever a body is on a free fall its weight is zero, but its mass remains unaltered.
Question 15.
Two masses are In the Nation 1:2. What is the ratio of their Inertia?
Answer:
Inertia of a body is directly proportional to its mass. Therefore the ratio of their inertia is Their inertia is also in the ration 1:2.
Question 16.
Passengers in buses tend to fall back as it accelerates. Why?
Answer:
Due to inertia, the passengers tend to continue their state of rest, when the bus moves by accelerating.
Question 17.
A cricket player catches the ball by moving his hand along the direction of the motion of the ball. Why?
Answer:
By moving his hand along the direction of motion of the ball, the player increases the time of contact, thus reduces the impulse felt.
Question 18.
A stone breaks the window glass, but a bullet make only a hole. Why?
Answer:
Since the velocity of the bullet is much greater than that of the stone, the bullet is in contact with the glass for a very short time that the glass can’t give enough resistance.
Question 19.
Can a moving body be in equilibrium?
Answer:
Yes, If a body is in a state of uniform motion in a straight line (net force acting on it is zero), its a moving body in equilibrium.
Question 20.
State law of conservation of momentum?
Answer:
When the net external force on a system is zero, then there is no change in momentum of the system.
![]()
Question 21.
What is friction?
Answer:
The property by virtue of which an opposing force is created between two bodies in contact, which opposes their relative motion is called friction.
Question 22.
What is frictional force?
Answer:
The force, which opposes the motion of one body over the other in contact with it, is called frictional force
Question 23.
What is static friction?
Answer:
Frictional force, which balances the applied force when the body is in the state of rest is called static friction.
Question 24.
What is limiting friction?
Answer:
The maximum static friction that a body can exert on the other body in contact with it is called limiting friction.
Question 25.
What is sliding friction?
Answer:
The frictional force that opposes the relative motion between the surfaces when one body slides over the other body is called sliding friction.
Question 26.
What is rolling friction?
Answer:
Rolling friction is defined as the force of friction acting when a body rolls over the other body.
Question 27.
Define angle of friction.
Answer:
Angle made by the resultant of normal reaction and limiting friction with the normal reaction is called angle of friction.
Question 28.
Define angle of repose.
Answer:
Angle of repose is defined as the angle that an inclined plane makes with the horizontal when a body placed on it just starts sliding.
![]()
Question 29.
Define coefficient of static friction.
Answer:
The coefficient of static friction is defined as the ratio of limiting friction to the normal reaction between the surfaces.
Question 30.
What are the units and dimensions of the coefficient of friction?
Answer:
Co-efficient of friction is a ratio, so it is unitless.
Question 31.
When a wheel is rolling, what is the direction of the friction?
Answer:
Friction is tangential to the wheel and in the direction opposite to motion.
Question 32.
Which of the following is a scalar quantity? Force, momentum & Inertia.
Answer:
Inertia.
Question 33.
If the string rotating stone is cut. Which direction will the stone move?
Answer:
The stone will move in the direction tangential from the point where it got cut.
Question 34.
Does a stone moving in a uniform circular motion (constant speed) has no net external force on it?
Answer:
The speed is uniform but direction is changing, so, there is a change in velocity (acceleration is non zero) Hence stone is under the influence of a net external force.
Question 35.
A man of mass 60 kg is on a lift which is moving up with uniform speed, [g = 10ms 2]. Find apparent weight?
Answer:
Since it is moving with uniform speed, there no additional force (a = 0) So, apparent weight = m(g + 0) = (60 kg) × (10 ms-2)
= 600 N.
Question 36.
What happens to the coefficient of friction if the weight of a body is doubled?
Answer:
The coefficient of friction remain constant.
Question 37.
What provides the centripetal force for a car taking a turn on a level road.
Answer:
Frictional force.
Question 38.
Find force on a body if change in momentum of a body is 20 kg ms-1 over 5 seconds.
Answer:
Force is the rate of change of momentum
F = \(\frac{\Delta(\text { momentum })}{t}\) = \(\frac{20 \mathrm{kg} \mathrm{ms}^{-1}}{5 \mathrm{s}}\) 4 N
Question 39.
A 50 kg mass is subjected to a force of 5 N. What is acceleration of the body.
Answer:
We know that, F = ma
⇒ α = \(\frac{F}{m}\)
= \(\frac{5 \mathrm{N}}{50 \mathrm{kg}}\) = 0.1 ms-1
![]()
Question 40.
A 25 g body is moving with uniform velocity of 5ms-1. What is the force acting on the body?
Answer:
Since there is no change in velocity the a = 0.
⇒ F = ma= (25 × 10-3) × (0) = 0 N
1st PUC Physics Laws of Motion Two Marks Questions and Answers
Question 1.
State the 4 basic forces of nature.
Answer:
- Gravitational force
- Elector magnetic force
- Strong nuclear force
- Weak nuclear force.
Question 2.
Which is the strongest & weakest force in nature?
Answer:
Strongest – strong nuclear force Weakest – gravitational force.
Question 3.
Explain why does a cyclist bends while riding a curved road?
Answer:
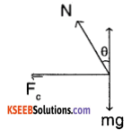
On bending the cyclist part of his normal force to acts as centrepetal force that helps him staying within the circular path.
Fa = N sin θ = \(\frac{m v^{2}}{\alpha}\)
Question 4.
Show that impulse of force is equal to the change in momentum of a body.
Answer:
Let a force F act on a body of mass ‘m’ for a short interval of time‘t’.
Then impulse of the force = F t
= mat = \(m\left(\frac{v-u}{t}\right) t\) = m (v – u). Therefore impulse of force is equal to the change in momentum.
Question 5.
Define Impulse of a force and Impulsive force.
Answer:
The product of the force & the time for which it acts on a body is called impulse of a force. The force acting on a body for short interval of time is called impulsive force.
Question 6.
A ball hits the ground with a momentum \(\overrightarrow{\mathbf{p}}\) and bounce back with the same magnitude of momentum. Find the change in momentum.
Answer:
Initial momentum = \(\overrightarrow{\mathbf{p}}\)
Final momentum = – \(\overrightarrow{\mathbf{p}}\)
change in momentum =
Δ p = – \(\overrightarrow{\mathbf{p}}\) – \(\overrightarrow{\mathbf{p}}\) =- 2\(\overrightarrow{\mathbf{p}}\)
![]()
Question 7.
While Jumping on a cement floor, we weigh less than what weighs on cement floor. Why?)
Answer:
When we are on the floor, exerts reaction on us. When we jump the reaction on us is zero. Therefore while jumping on a cement Floor we weigh less than on cement floor.
Question 8.
Distinguish between conservative and nonconservative force.
Answer:
Conservative forces are those forces against which the work done doesn’t depend on the path followed but depends only on the initial and final positions. Non-conservative forces are those in which the work done depends on the path taken
Question 9.
Calculate the Impulse of a force of 50 N acting for 0:1s.
Answer:
F = 50N t = 0:1 s
impulse = 50 N × 0.1s= 5 Ns
Question 10.
What are the methods of reducing friction?
Answer:
- Friction between two surfaces can be reduced by polishing them.
- Jets, aeroplanes, and cars are given streamlined shape to reduce friction due to air resistance.
- The use of lubricants like oil, grease, etc. reduces the friction in machines.
- By using ball bearings friction in wheels of a car or cycle can be minimised.
Question 11.
Static friction is a self-adjusting force comment.
Answer:
The magnitude of static friction depends? on the magnitude of the applied force. As the applied force increases the magnitude of the static friction also increases. Thus static frictional force is a self-adjusting force.
Question 12.
Write two advantages of friction.
Answer:
- Brakes of the vehicles work due to friction.
- Friction helps in driving vehicles.
- A match stick is lighted because of friction.
Question 13.
Is earth an inertial frame of reference?
Answer:
No. earth can not be considered as an inertial frame of reference, because the earth is rotating and revolving, which means it is accelerating.
Question 14.
Derive an expression for recoil velocity of gun.
Answer:
Let mg be mass of gun,
\(\vec{v}_{g}\) = recoil velocity of gun,
mb be mass of Bullet \(\vec{v}_{b}\)
Initial momentum = 0,
Final momentum = mg \(\vec{v}_{g}\) + mb \(\vec{v}_{b}\)
By law of conservation of momentum
0 = mg \(\vec{v}_{g}\) + mb \(\vec{v}_{b}\)
⇒ \(\vec{v}_{b}\) = – \(\left(\frac{m_{b} \vec{v}_{b}}{\vec{m}_{g}}\right)\)
Question 15.
How does lubricants help in reducing friction?
Answer:
The lubricants spread over the irregularities on the surface that makes the contact. So, the contact between the lubricant and the moving objects reduces the friction.
Question 16.
A bubble generator is kept at the bottom of an aquarium which is on a free fall. Will the bubbles generated rise to the top?
Answer:
No, the bubbles generated at the bottom will not rise to the surface, ‘this is because the water in the aquarium is in a state of weightlessness and does not give the bubbles a reactional upward force.
![]()
Question 17.
Why is it easier to pull a roller than push it?
Answer:
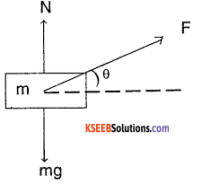
When we pull, the force ‘F’ the normal force is reduced by a value F sin θ. So the friction experienced is lesser which makes it is easier to pull.
Question 18.
An object of mass m collides with a another object of mass ‘2 m’. if the initial velocity of the object of mass ‘m’ is v1 and of mass ‘2m’ is ‘0’. Then find the final velocity assuming they get stick to each other.
Answer:
Initial momentum =
(m) (v1) + (2m) × (0)
= mv1
Final momentum= m(vx) + 2m (vx)
= 3m vx.
Where Vx is the velocitycombined mass By Law of conservation of momentum
mv1 = 3mvx
vx = \(\frac{m v_{1}}{3 m}\)
vx = \(\frac{v_{1}}{3}\)
Question 19.
If a boats sail is blown by air produced by a fan on the boat, can the boat move forward?
Answer:
No, the boat can not be moved by a fan on the boat, this is because when the fan pushes the sail blowing air, the air pushes the fan backwards with the same force. Since there is no external force on the system – the net change in momentum is zero.
Question 20.
A retarding force Is applied to a motor car. If speed Is doubled how much more distance will it travel.
Answer:
Let original force be F1, mass be m1 velocity be V and distance be S then,
F = ma, & V² = 2as
⇒ F = \(\frac{m v^{2}}{2 s}\) ⇒ S = \(\frac{m v^{2}}{2 F}\)
If velocity is doubled, then the distance it will travel before coming to halt will be increased by 4 times.
1st PUC Physics Laws of Motion Three Marks Questions and Answers
Question 1.
Distinguish between mass and weight.
Answer:
- Mass is the amount of matter contained in a body while weight is the gravitational force acting on a body.
- Mass of body remains same while weight of body varies from place to place.
- Mass is a scalar but weight is a vector.
- Unit of mass is kilogram and that of weight is newton.
- Mass is measured using a physical balance and weight is measured using a spring balance.
Question 2.
Derive the equation F = ma.
Answer:
Consider a body of mass ‘m’ moving with a velocity ‘u’. Let a constant force ‘F’ applied on a body changes its velocity to V in ‘t’ seconds.
Initial momentum of the body = mass × initial velocity = m u
Final momentum = mass × Final velocity = m v
Change of momentum in ‘t’ seconds = mv – mu.
= \(\frac{m v-m u}{t}\) = m \(\left(\frac{v-u}{t}\right)\)
∴ α = ma
∵ \(\frac{v-u}{t}\) = a, acceleration
According to Newton’s second law, the rate of change of momentum is directly proportional to the applied force or vice versa.
i. e. Force a rate of change of momentum
F α ma
F = kma
Where ‘k’ is a proportionality constant. In SI system k=1.
∴ F = ma
Question 3.
State and explain Newton’s third law of motion. Give illustrations for the same.
Answer:
Newton’s third law states that for every action, there is an equal and opposite reaction.
Let F1 be the force exerted by the body A on body B, F1 is called action. Then force F2 exerted by B on A is called reaction. According to the third law F1 = – F2.
Illustrations:
- When a book is placed on the table the weight of the book is acting vertically downwards (action). The table exerts an equal and opposite force vertically upwards (reaction).
- A swimmer pushes the water in the backward direction with a certain force (action) and the water pushes him in the forward direction with equal and opposite force (reaction).
- The sailing of a boat is due to the action of the boat on water and reaction from water on the boat.
- When an object is suspended from the string, the weight of the object acts vertically downwards. The reaction in the string called the tension acts vertically upwards.
- The earth attracts the moon with a force that constitutes action. In turn the moon attracts earth with equal and opposite force (reaction).
Question 4.
Derive a relation for the safe velocity of negotiating a curve by a body in a banked curve with fractional coefficient ‘µ’.
Answer:
The net force along the x-direction inwards should provide the centripetal force
∴ Ffriction cos θ + N sin θ = \(\frac{m v^{2}}{2}\) → (1)
∵ there is is no motion in y-direction
N cos θ Ffriction sin θ = mg → (2)
we know that
Ffriction = µ N.
divide (1) by (2)
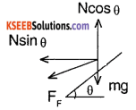
\(\frac{\mu \mathrm{N} \cos \theta+\mathrm{N} \sin \theta}{\mathrm{N} \cos \theta-\mu \mathrm{N} \sin \theta}\) = \(\frac{m v^{2}}{r(m g)}\)
⇒ \(\frac{N(\mu+\tan \theta)}{N(1-\mu \tan \theta)}\) = \(\frac{\mathrm{v}^{2}}{\mathrm{rg}}\)
⇒ v² = rg\(\left(\frac{\mu+\tan \theta}{1-\mu \tan \theta}\right)\)
The max velocity to safely negotiate the turn is \(\sqrt{r g\left(\frac{\mu+\tan \theta}{1-\mu \tan \theta}\right)}\)
![]()
Question 5.
Write the equation corresponding to the ones given, for rotational motion about a fixed axis.
(i) x (t) = x (0) + v (0) t + 1a/2 t²
Answer:
θ (t) = θ (0) + ω(0) + \(\frac{1}{2}\) α t²
(ii) v² (t) = v² (0) + 2a [x t) – x (0)]
Answer:
ω² (t) = ω² (0) + 2 a α [θ (t) – θ (0)]
(iii) \(\overline{\mathbf{v}}\) = \(\frac{v(t)-v(0)}{2}\)
Answer:
\(\bar{\omega}\) = \(\frac{\omega(t)-\omega(0)}{2}\)
(iv) v(t) = v(0) + at
Answer:
ω (t) = ω (0) + α t
Question 6.
Two masses m1 and m2 are connected to ends of string passing over a pulley. Find tension and acceleration associated.
Answer:
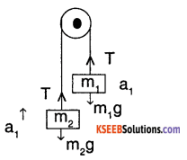
Assuming mass mt moves down with an
acceleration ‘a’
m1g -T = m1a1 ………….. (1)
T – m2 g = m2 a1 ………. (2)
(1) + (2)
m1g – m2g = (m1 + m2) a1
⇒ a1 = \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right) g\)
& T = m1g – m1 \(\left(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right) g\right)\)
⇒ T = m1g \(\left[1-\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right]\)
T = \(\frac{2 m_{1} m_{2} g}{m_{1}+m_{2}}\)
Question 7.
Name a mass varying system. Derive an expression for the velocity of the rocket at any instant of time
Answer:
A rocket-propelled into space is a mass varying system as it losses the weight of the fuel burnt.
Let the velocity of gas used for propelling be ‘vg’ & let the rate of decrease in mass of the body be \(\frac{\mathrm{d} m}{\mathrm{dt}}\)
Then, by law of conservation of momentum since initial momentum is zero, dp = 0
⇒ d (mv) = 0
⇒ (dm) v + m d v = 0
⇒ vdm = – mdv ⇒ dm = – \(\frac{\mathrm{d} \mathrm{v}}{\mathrm{v}}\)
Integrating on both sides
v = vg (Inm) + c
⇒ v = – vg logc m + c
where c is a constant.
Question 8.
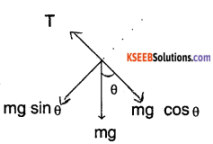
Indicate the force acting on a block of mass ‘m’ at rest on an Inclined plane of angle θ.
Answer:
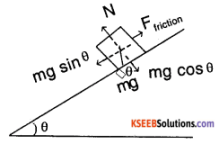
Ffriction = μ N, N = mg cos θ & mg sin θ = Ffriction
Question 9.
Distinguish between static friction, limiting friction & kinetic friction. How do they vary with applied force? Explain.
Answer:
The static friction is a friction that acts on a body at rest.
Limiting friction is the maximum value of static friction. It is the force that is required for the body to just start moving.
Kinetic friction is the frictional force that action a body which is in motion.
On increasing the applied force, static friction increase, until it reaches limiting friction which is fixed, and kinetic friction also remains constant.
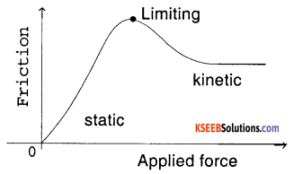
Question 10.
Define Impulse. What graphical methods can be used to calculate impulse in the following cases
- constant force
- variable force acting on a body
Answer:
Impulse is a force that acts a body for a very short duration of time. It is defined as the product of force and the time for which it acts.
1.
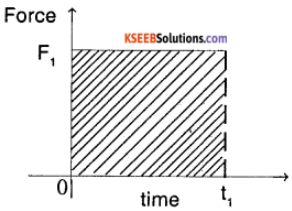
In case of a constant force, say F1, the impulse is simply product of force and duration
Impulse = F1 × t1
2.
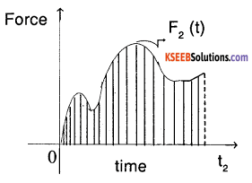
In case of a variable force, the impulse will be the integral of F2 one of the interval [0,t2]
Impulse = \(\int_{0}^{t_{2}} F_{2}(t) d t\)
Question 11.
An object of mass ‘m’ is on a inclined plane (θ). Find
- The effective resistant force on the body if it’s moving downwards.
- The minimum force if it is being pushed upwards.
Assume a friction with a coefficient of μ
Answer:
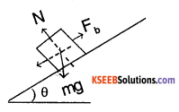
1. The net force along the slope is
⇒ Feq = F1 – Mg sin θ
= μ N – Mg sin θ
But, N = mg cos θ
⇒ Feq = mg (μ cos θ – sin θ)
2. Additional force required be Fa
Fa = mg sin θ + μ N
= mg sin θ + μ mg cos θ
⇒ Fa = mg (sin θ + μ cos θ)
1st PUC Physics Laws of Motion Five Marks Questions and Answers
Question 1.
State and prove the law of conservation of momentum.
Answer:
In a closed system, the total linear momentum of the system remains constant or conserved.
Proof:
Consider two bodies A and B of masses m1 and m2 moving in the same direction with uniform velocities u1 and u2 respectively. After the collision let their uniform velocities be v1 and v2. Let‘t’ be the time of impact.
Change in momentum of A
= m1v1 – m1u1
Rate of change of momentum of A
= \(\frac{m_{1} v_{1}-m_{1} \mu_{1}}{t}\)
change in momentum of B
= m2v2 – m2u2
Rate of change of momentum of B
= \(\frac{m_{2} v_{2}-m_{2} u_{2}}{t}\)
If F1 is the force exerted by A on B then according to second law,
F1 = \(\frac{m_{2} v_{2}-m_{2} u_{2}}{t}\) (action)
If F2 is the force exerted by B on A then
F2 = \(\frac{m_{1} v_{1}-m_{1} \mu_{1}}{t}\) (reaction)
According to Newton’s third law, action and reaction are equal and opposite i.e.
F1 = – F2
\(\left[\frac{m_{2} v_{2}-m_{2} u_{2}}{t}\right]\) = – \(\left[\frac{m_{1} v_{1}-m_{1} \mu_{1}}{t}\right]\)
m2v2 – m2u2 = – m1v1 + m1u1
OR
m1u1 + m2u2 = m1v1 + m2v2
i.e., Total momentum before collision = Total momentum after collision. Hence the momentum is conserved.
![]()
Question 2.
A stone weighing 5kg. falls from the top of a tower 100m high and buries itself 1 m deep in the sand. What is the average resistance offered by sand?
Answer:
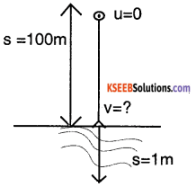
Mass of the stone, m = 5kg
Height of the tower h = s = 100m
Initial velocity u =0
Final velocity v = ?
From the relation, v² = u² + 2gs
v² = 0 + 2 × 9.8 × 100
v² = 1960
V = \(\sqrt{1960}\)
v = 44.27 ms-1
Then the stone penetrates through the sand with a initial velocity, u = 44.27 ms-1
Distance travelled, S = 1 m
Final velocity, v = 0
acceleration, a =?
From the equation, V² = u²+2as
0² = (44.27)² + 2 × a × 1
– 1960 = 2a
a = -980ms-2
∴ The average resistance offered by the sand is F = ma
= 5 × 980
F = 4900 N
Question 3.
State the Newton’s laws of motion. Write any two illustrations.
Answer:
Newton’s first law of motion states that, everybody continues to be in its state of rest or uniform motion along a straight line unless compelled to change its state by an external force. Newton’s second law of motion states that the rate of change of momentum of a body is directly proportional to the applied force and takes place in the direction of the force.
Newton’s third law of motion states that for every action there is. an equal and opposite reaction.
Illustrations for Newton’s third law of motion are
- when a book is placed on the table the book exerts force on the table (action), in turn the table exerts an equal and opposite force (reaction) on the book in the upward direction.
- The sailing of a boat is due to the action of the boat on water and the reaction from water on boat.
Question 4.
Consider a body of mass ‘m’ attached to a string of length ‘L’. If the ring is forming a vertical circle, derive an expression for velocity and tension at any point.
Also, find the velocity that is required for mass to just reach the peak point of the circle.
Answer:
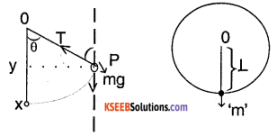
Let ‘θ’ be the angle the string makes with the vertical at any instant of time. Let vx be the velocity of body at the lowermost point x. The distance traveled by the body from the given point ‘p’ to ‘X’ in ‘y’ direction is given by,
XY = L – Lcos θ = L(1 – cos θ)
T – mg cos θ = \(\frac{m v^{2}}{L}\)
Using the equation v² = u² + 2as, we can write
Vx² = v² + 2g (XY)
i.e. V² = Vx² – 2g L (1 – cos θ) ……….. (1)
Tension, T = mg cos θ + \(\frac{m v^{2}}{L}\) using (1)
T = mg cos θ + \(\frac{m}{L}\) (Vx² – 2gL (1 – cos θ)
= mg cos θ + \(\frac{m v_{x}^{2}}{L}\) – 2 mg (1 – cos θ)
T = \(\frac{m v_{x}^{2}}{L}\) + mg (3 cos θ – 2)
For the vertical circle to be reached v = 0 & vx = ? & θ = 180°
⇒ vx² = v² + 2g L (1 – cos θ)
vx² = 0 + 2g L (1 – (- 1))
vx = \(\sqrt{4g L}\)
vx = \(2 \sqrt{g L}\)
Question 5.
If the system Is on a frictionless surface. Find the ratio of tensions in the string.
Answer:
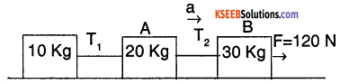
The acceleration of the system is given
by a = \(\frac{\text { Force applied }}{\text { Total mass }}\)
= \(\frac{120 \mathrm{N}}{(10+20+30) \mathrm{kg}}\) = 2 ms-2
For the last block
120 – T2 = ma
⇒ T2 = 120- (30) × (2)
= 60 N
For the middle block
T2 – T1 = ma
60 – T1 = (20) × (2)
T1 = 60 – 40 = 20 N
The ratio of tensions is,
T1 : T2 = 20 : 60 = 1 : 3
Question 6.
For the figure shown, find acceleration produced and the force of contact between the blocks. What is the effect of this force if it is applied to other blocks.
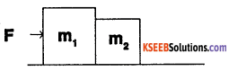
Answer:
The acceleration of system is
a = \(\frac{F}{\left(m_{1}+m_{2}\right)}\)
When the force is applied on block m, we have,
F – Fc = m1 a
where Fc is force of contact
⇒ Fc = F – m1 \(\left(\frac{F}{m_{1}+m_{2}}\right)\) = \(\left(\frac{F m_{2}}{m_{1}+m_{2}}\right)\)
If F is applied to other block ,
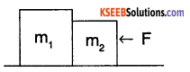
Fc = m1 a = \(\left(\frac{\mathrm{m}_{1}}{\mathrm{m}_{1}+\mathrm{m}_{2}}\right)\) F
Question 7.
In the system shown if μk (kinetic friction coefficient) is 0.04. Find acceleration of the trolley,
[g = 10ms-2]
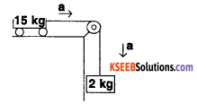
Answer:
Free body diagram of trolley
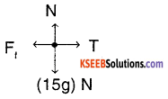
We know that Ff = μ N
= μk mg
= 0.04 × 15 × 10
= 6N
⇒ T – 6N = ma
= 15 × a
⇒ T – 5 a = 6 …………. (1)
Free body diagram of mass
⇒ 2g – T = ma
⇒ 20 – T = 20
⇒ 2a + T = 20 ……….. (2)
0n,(1) – (2)
– 17 a = – 14
a = \(\frac{14}{17}\) = 0.82ms-2
![]()
Question 8.
Weights of 250 g & 200 g are connected by a string over a smooth pulley. I system is traveling 4.95 m in the first 3 second. Find the value of g.
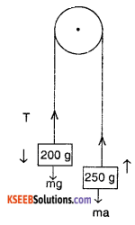
Answer:
For the pulley system,
T – (200 g × 10-3) g = (200 × 10-3kg) a
T – (0.29) = 0.2a …………….(1)
an (0.25g) – T = (0.25a) …………(2)
⇒ From (1) & (2)
0.45 a = (0.25 – 0.2) g
a = \(\frac{0.05}{0.45}\)g = \(\frac{g}{9}\) ms-2
Now, S = 4.95 m, t = 3s u = 0
From S = ut + \(\frac{1}{2}\) at²
4.95 = 0 + \(\frac{1}{2}\) × a × (3)²
4.95 = \(\frac{1}{2}\) × \(\frac{10}{9}\) × g × 9²
g = \(\frac{4.95}{5}\) = 9.9 ms-2
Question 9.
A force of 80N acting on a body at rest for 2 sec imparts it a velocity of 20ms-1 what is the mass of the body calculate the distance traveled by the body in 2 seconds?
Answer:
Force, F = 80N
Initial velocity, u =0
Time for which force acts on the body, t = 25s,
Final velocity, v = 20ms-1
From the equation v = u + at
20 = 0 + a × 2
a = 10ms-2
∴ The mass of the body, from the equation F = ma
m = \(\frac{F}{a}\) = \(\frac{80}{10}\) = 8kg
∴ The distance travelled by the body in a time, t = 2s. From the equation
s = ut + \(\frac{1}{2}\) at²
= 0 × 2 + \(\frac{1}{2}\) × 10 × 2²
= 0 + 20 = 20m.
Question 10.
A man of 60 kg is standing on a weighing machine placed on the floor of a lift which reads the force in newtons. Find the reading of the weighing machine when the lift is
- stationary
- moving upwards with uniform speed of 10 ms-1
- moving downwards with uniform acceleration of 5 ms-2
- moving upwards with uniform acceleration of 5 ms-2.
- What would be the reading of the weighing machine if the connecting rope of the lift suddenly breaks and lift begins to fall freely under gravity, g = 10 ms-2.
Answer:
Weight of the man is due to the reaction from the floor of the lift. It is given by,
R = mg + ma*
where a* is the acceleration of the lift.
1. when the lift is at rest a* = 0
∴ Reading of the weighing machine
R = mg = 60 × 10 = 600 N.
2. when the lift is moving up or down with uniform velocity, a* = 0
∴ Reading of the weighing machine,
R = 600 N.
3. When the lift is moving downwards with an acceleration a*.
R = mg – ma* = m(g – a*)
= 60 × (10 – 5) = 300 N.
4. When the lift is moving upwards with acceleration a*,
R = mg + ma* = m(g + a*)
= 60 × (10 + 5)
= 900 N.
5. If the lift falls freely under gravity, a* = g
∴ R = m(g – a*) = 0.
Question 11.
A rubber ball of mass 0.1 Kg is dropped on the ground from a height of 2.5 m and it rises to a height of 0.4m. Assuming the time of contact with the ground to be 0.01 s, calculate the force exerted by the ground on the wall, g = 10ms-2
Answer:
Mass of the ball m = 0.1 kg
Time in contact with the ground, t = 0.01s
1. When the ball is dropped on ground,
u =0, s = 2.5m, g = 10ms-2
From the equation, v² = u² + 2gs
v² = 0 + 2 × 10 × 2.5
v = 7.07ms-1, downwards.
2. When the ball rises up from the ground,
v = 0, s = 0.4m, g = 10ms-2
From the equation v² = u² + 2gs
0 = u² + 2(- 10)0.4
u² = 8
u =2.83ms-1, upwards.
Assuming the upward velocity +ve & downward velocity -ve,
change of velocity = 2.83 – (- 7.07)
i.e v – u = 9.9ms-1
∴ Force exerted by the ground on the ball is,
F = m \(\left(\frac{v-u}{t}\right)\) = 0.1 \(\left(\frac{9.9}{0.01}\right)\) = 99 N.
Question 12.
A Bullet flying with a velocity of 50ms-1 hits a block of wood and penetrates through a distance of 0.2 m before coming to rest. The Mass of the bullet is 0.03kg. Calculate the resistance offered by the block of wood.
Answer:
Initial velocity, u = 50ms-1
Distance travelled, s = 0.2
Final velocity v = 0
Mass of the bullet, m = 0.03 kg
From the equation, v² = u² + 2as
0 = 50² + 2 × a × 0.2
a = – \(\frac{2500}{0.4}\) = -6250ms-2
∴ The resistance offered by the wood is
F = ma = 0.03 × 6250 = 187.5 N.
Question 13.
A machine gun fires 200 bullets per minute with a velocity of 60ms-1. If the mass of each bullet Is 0.02kg, calculate the power of the gun.
Answer:
Number of bullets fired in one minute = 200
work done by the gun in one minute is,
W = kinetic energy of 200 bullets
W = 200 (\(\frac{1}{2}\)mv²)
= 200 × \(\frac{1}{2}\) × 0.02 × (60)²
= 7200J
∴ Power, P = \(\frac{W}{t}\), t = 60 seconds
P = \(\frac{7200}{60}\) = 120 watt.
∴ Power of the gun = 120 watts.
Question 14.
Two metal balls of masses 10kg and 8kg are moving In the same direction with velocities 10m/s and 4m/s respectively. They stick together after collision. Find their common velocity after collision. If they are moving
- In the same direction,
- In opposite direction before collision.
Answer:
m1 = 10kg, m2 = 8kg
u1 = 10m/s and u2= 4m/s.
1. v1 = v2 = v, common velocity.
m1u1 +m2u2 = m1v1 + m2v2
10 × 10 + 8 × 4 = (l0 + 8)v
or v = 7.33m/s
2. m1u1 – m2u2 = (m1 + m2) v
10 × 10 – 8 × 4 = (10 + 8)v
v = 3.778m/s.
Question 15.
Derive the equation F = ma.
Answer:
Consider a body of mass ‘m’ moving with a velocity ‘u’. Let a constant force ‘F’ applied on a body changes its velocity to ‘v’ in ‘t’ seconds.
Initial momentum of the body = mass × initial velocity = m u
Final momentum = mass × Final velocity = m v
Change of momentum in ‘t’ seconds = mv – mu.
Rate of change of momentum
= \(\frac{m v-m u}{t}\) = m\(\left(\frac{v-u}{t}\right)\) = ma
∵ \(\frac{v-u}{t}\) = a, acceleration
According to Newton’s second law, the rate of change of momentum is directly proportional to the applied force or vice versa.
i.e. Force a rate of change of momentum
F α ma
F = kma
Where ‘k’ is a proportionality constant. In SI system k =1.
∴ F = ma.
![]()
Question 16.
Name the basic forces in nature.
Answer:
Basic forces in nature are,
- Gravitational force
- Electromagnetic force
- Nuclear force and
- Weak force
Question 17.
A body is moving on a frictionless curved path of radius of 1.8 km with a speed of 30 ms-1. Find the banking angle required.
Answer:
The centripetal force required to keep the body in circular motion is \(\frac{m v^{2}}{r}\)
Here, v = 30 ms-1
r = \(\frac{1.8 \times 10^{3} m}{2}\) = 0.9 103 = 900m
N cos θ = mg
and \(\frac{m v^{2}}{r}\) = N sin θ
⇒ \(\frac{m v^{2}}{r}\) = \(\frac{m g}{\cos \theta}\) sin θ
⇒ tan θ = \(\frac{v^{2}}{r g}\)
⇒ θ = tan-1 \(\left(\frac{30^{2}}{900 \times 10}\right)\)
⇒ θ = tan-1 (0.1) = 5.71°.
Question 18.
What is the acceleration of a body moving on a circular path of radius 400 m. If it has
- constant speed of 40 ms-1
- speed increases at 3 ms-2
Answer:
A body on a circular path has two kinds of accelerations: radial & linear
1. If speed is constant linear acceleration is zero & radical acceleration is ar = \(\frac{v^{2}}{r}\)
v = 40ms-2
r = 400 m ⇒ ar = \(\frac{40 \times 40}{400}\) = 4ms-2
2. If the speed increases at 3 m/s², it has a linear acceleration of 3ms-2
a = \(\sqrt{a_{r}^{2}+a_{1}^{2}}\)
= \(\sqrt{3^{2}+4^{2}}\)
= 5 ms-2.
Question 19.
An aeroplane at 360 km hr-1 has its wing banked at an angle 20°. Find the radius of the circle traversed by the plane, [g = 10ms-2]
Answer:
Speed of the plane = 360 km/hr
= \(\frac{360 \times 10^{3}}{3600}\) = 100 ms -1
we know that tan θ = \(\frac{v^{2}}{r g}\)
⇒ r = \(\frac{v^{2}}{\tan \theta \times g}\) = \(\frac{100 \times 100}{\tan \left(20^{\circ}\right) \times 10}\)
= 2.747 km.
Question 20.
A uniform chain of length L is kept on a table of coefficient of static friction μ(limiting value). Find the maximum length of chain that can be outside the table, without it sliding away.
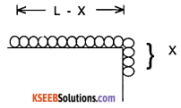
Answer:
Let x be the length of the chain that can be outside the table.
Let ‘M’ be the total mass of the chain.
Mass on the table is \(\frac{M}{L}\)(L – x)
Mass of the chain outside = \(\frac{M}{L}\) x
For, equilibrium,
Force of friction = weight of the hanging part.
i.e., μN = \(\left(\frac{M}{L} x\right)\)g × α
i.e., μ\(\left(\frac{M}{L}(L-x) g\right)\) = \(\left(\frac{M}{L} x\right)\)g
μ(L – x) = x or x = \(\frac{\mu L}{1+\mu}\)
Question 21.
For the system shown in the figure, the coefficient of Kinetic friction between the mass and plane is 0.25.
Given that M2 = 5kg & M3 = 7kg. Find M1, such that the body M1, is moving with uniform velocity. Sin37° = \(\frac{3}{5}\), cos 37° = \(\frac{4}{5}\)
Answer:
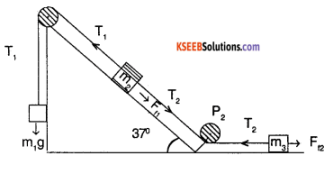
For the mass m1 to have a uniform velocity the system should be in equilibrium.
⇒ T1 = m1 g
T1 = 10m1 …………… (1) (g =10 m/s²)
T1 =T2 + F11 + m2 g sin θ
= T2 + μ N + m2 g sin 37°
= T2 + μm2g cos 37° + m2g sin 37°
= T2 + m2g \(\left(\mu \frac{4}{5}+\frac{3}{5}\right)\) (g =10 m/s²)
T1 = T2 + m2[8μ + 6] ………….. (2)
T2 = F12
T2 = μ N
= μ m3 g
T2 = (0.25) (7) (10)
T2 = 17.5 N ………….. (3)
Substituting (1) & (3) in (2)
10m1 = 17.5 + 5 [8(0.25) + 6]
10m1 = 57.5 N
m1 = 5.75 kg.
1st PUC Physics Laws of Motion Numerical Problems Questions and Answers
Question 1.
Two masses 4 kg & 2 kg are connected by a massless string and they are placed on a smooth surface. The 2 kg mass is pulled by a force of 12 N as shown
- Find the acceleration of the system.
- If the string is replaced by a spring then what change do you notice in the acceleration
- In the string, system find the Tension

Answer:
1. We know that from Newtons second Law,
F = ma
F Force on the system
⇒ a = \(\frac{F}{m}\) = \(\frac{\text { Force on the system }}{\text { Total mass }}\)
= \(\frac{12 \mathrm{N}}{(4+2) \mathrm{kg}}\)
a = 2 ms-2
2. If the string is replaced by spring, there is no change in mass of system. So there is no change in the acceleration a = 2m s-2
c) We know that, F = m a
(12 – T) = (m a)
T = 12 – (2 × 2)
T = 8 N
a = 2 ms-2
Question 2.
A force of 98 N acts on a body of mass 10 kg which is at rest. Calculate
- Velocity at the end of 5 seconds.
- Distance traveled by the body in 5 seconds.
Solution:
1. To find the velocity at the end of 5 seconds.
We have, F = ma
Given, F = 98 N and
m = 10 kg
∴acceleration a = \(\frac{F}{m}\) = \(\frac{98}{10}\)
= 9.8 ms-2
velocity v = u + at
Here a = 0,
a = 9.8 ms-2 and
t = 5 s
∴ v = 0 + 9.8 × 5
= 49.0 ms-1
2. To find the distance travelled
we have, s = ut + \(\frac{1}{2}\) at²
Here, u = 0,
a = 9.8 ms-2
t = 5 seconds
∴ s = 0 × 5 + \(\frac{1}{2}\) × 9.8 × (5)²
= 122.5 m.
Question 3.
A truck of mass 3000 kg is moving with a velocity of 10 m/s is accelerated by a force of 600N.
- What is the rate at which its velocity increases?
- How far will it travel In 10s?
Solution:
1. To find the rate at which velocity is increasing
Force F = 600 N
mass m = 3000 kg
Rate of increase in speed,
a = \(\frac{F}{m}\)
= \(\frac{600}{3000}\)
= 0.2 ms-2
2. To find the distance travelled in 10 s
We have, s = ut + \(\frac{1}{2}\) at²
Here, u =10 ms-1
t = 10 s
a = 0.2 ms-2
∴ s = 10 × 10 + \(\frac{1}{2}\) × 0.2 × (10)²
= 100 + 10
= 110 m.
Question 4.
A certain force acting on a body of mass 10 kg at rest moves it through 125 m in 5 seconds. If the same force acts on a body of mass 15 kg, what is the acceleration produced?
Solution:
in the case of the first body,
u = 0;
t = 5 s;
s = 125 m
Substituting these values in the equation,
s = ut + \(\frac{1}{2}\) at
125 = 0 × 5 + \(\frac{1}{2}\) × a × (5)²
\(\frac{1}{2}\) × a × 25
∴ a = \(\frac{2 \times 125}{25}\) = 10 ms-2
F = m × a = 10 × 10 = 100 N
If the same force acts on another body of mass 15 kg, the amount of acceleration produced is,
a = \(\frac{F}{m}\) = \(\frac{100}{15}\)
= 6.67 ms-2
![]()
Question 5.
A cricket ball of mass 0.15 kg is moving with a velocity of 12 ms-1 and is hit by a bat so that the ball is turned back with a velocity of 20 ms-1. If the force of blow acts for 0.01 s, find the average force exerted on the ball by the bat.
Solution:
Initial velocity u = 12 ms-1
Final velocity v = 20 ms-1
Change in velocity =20 – (- 12)
= 20 + 12
= 32 ms-1
(-ve sign is taken because initial and final velocities are in opposite direction)
Time for which force is acting, t = 0.01 s
∴ acceleration a = \(\frac{\text { change in velocity }}{\text { time }}\)
= \(\frac{32}{0.01}\)
= 3200 ms-2
Force F = ma
= 0.15 × 3200
= 480 N.
Question 6.
A hammer of mass 1 kg moving with a speed of 6 ms-1 strikes a wall and comes to rest in 0.1 s. Find the
- Impulse
- Retarding force on the hammer
- Retardation
Solution:
1. The initial momantum of the hammer is,
m × v = 1 kg × 6 m s-1
= 6 kg m s-1
= 6 Ns
Impulse = F . t = Δ P
= 0 – mv
= – 6 Ns.
2. The force on the hammer
F = \(\frac{\text { Impulse }}{\text { time }}\) =\(\frac{6 \mathrm{Ns}}{0.1 \mathrm{s}}\)
60 N.
3. Retardation = a =\(\frac{F}{m}\) = \(\frac{60 \mathrm{N}}{1 \mathrm{kg}}\)
= 60 m s-2
Question 7.
A disc of mass 200 g is kept floating horizontally by throwing 40 pebbles per second against it from below. If the mass of each pebble is 2g, calculate the velocity with which the pebbles are striking the disc. Assume the pebbles strike the disc normally and rebound with the same speed.
Solution:
Mass of the disc M = 200 g
= 0.2 kg
Total downward force
F = Mg
= 0.2 × 9.8 =1.96 N
Mass of one pebble m = 2 g = 2 × 10-3 kg Let v be the velocity with which the pebbles strike the disc. Momentum given by one pebble = mv The pebbles rebound downward and strike from below.
∴ net momentum given to the disc in the upward direction
= change in velocity of the pebble × m = (2v) m
Total momentum given in one second
=40 × m × 2v
= 80 mv
The disc remains horizontal if this is equal to the weight of the disc, Mg
∴ 80 mv = Mg
80 × 2 × 10-3 × v = 1.96
v = 12.25 ms-1
Question 8.
Water ejects with a speed of 0.2 ms-1 through a pipe of area of cross-section 1 × 10-2 m². If the water strikes a wall normally, calculate the force on the wall in newtons, assuming the velocity of the water normal to the wall is zero after the collision.
Solution:
Volume of water striking the wall per second = 0.2 × 10-2 = 2 × 10-3 m3
Mass of the water striking the wall in one second = volume × density = 2 × 10-3 × 1000
= 2 kg
Change in velocity of water on striking the wall in one second = 0.2 – 0 = 0.2 ms-1
Force acting on the wall
= change in momentum
=2 × 0.2
= 0.4N.
Question 9.
A gun of mass 5 tons fires a bullet of mass 20g with a velocity of 110.2ms-1. Find the velocity of the gun.
Solution:
Initially, both the gun and the bullet are at rest.
∴ The total initial momentum of the system is f zero.
If v1 and v2 are the final velocity of the gun and the bullet, final momentum is given by,
pf = m1v1 + m2v2
According to the law of conservation of momentum, pi = pf
m1v1 + m2v2 = 0
i.e., v1 = – \(\frac{m_{2} v_{2}}{m_{1}}\)
= \(\frac{-20 \times 110.2}{5 \times 1000}\)
= – 0.44 ms-1
∴ Recoil velocity of the gun is 0.44 ms-1.
Question 10.
A gun weighing 1000 kg recoils with a velocity of 3 × 10-2 m/s when a shell of mass 1 kg is shot from it. If the shell hits the target in 8 seconds, find the gun target distance.
Solution:
Initial momentum of the gun & that of shell is zero as they are at rest.
Recoil velocity of the gun v1 = – 3 × 10-2ms-1
Mass of the gun m1 = 1000kg
Mass of the shell m2 = 1 kg
velocity of the shell v2 =?
From the equation
m1 u1 + m2 u2 = m1v1 + m2 v2
0 = 1000(- 3 × 10-2) +1 .v2
∴ v2 = 30ms-1
The gun target distance,
s = v2 × t
= 30 × 8
= 240m.
Question 11.
A machine gun has a mass of 20 kg. The firing rate of 500 bullets per second and mass of each bullet Is 20 g. If the speed of the bullets 500 m s-1. Find the force required to keep the gun in its position.
Solution:
mgun = 20 kg, mb = 20 g
vgun = ? vb = 500 ms-1
From Law of conservation of momentum
Mgun Vgun + mb vb = 0
⇒ Vgun = –\(\frac{20 \times 10^{-3} \times 500}{20}\)
= – 0.5 -1
∴ Force required to hold its position
F = m\(\left(\frac{v-u}{t}\right)\) = 20 × \(\frac{(0.5-0)}{\left(\frac{1}{500}\right) s}\) = 5000 N
Question 12.
A body of mass 20 kg moving with a velocity of 10 ms-1 collides with another body of mass 40 kg moving In the same direction with a velocity of 5 ms-1. If both the bodies stick together after the collision, find the common velocity after collision.
Solution:
If u1 and u2 are the initial velocities of the two bodies before the collision, the total momentum before the collision is
pi = m1u1 + m2u2
Let v be the common velocity of the two bodies after collision. Then the final mo-mentum after collision is,
pf = (m1 + m2)v
From the law of conservation of momentum
Pi = Pf
m1u1 + m2u2 = ( m1 + m2) v

= 6.67 ms-1.
Question 13.
A shell of mass 10 kg flying horizontally with a velocity of 36 kmph explodes in air into two fragments. The larger fragment has a velocity of 25ms-1 & is directed In the same direction as the initial velocity of the shell. The smaller fragment has a velocity of 12.5 ms-1 in the opposite direction. Find the masses of the fragments.
Solution:
Let the mass of larger fragment be m1 = x Then the mass of smaller fragment is m2 = 10 – x
Initial velocity of larger fragment,
u1 = 36kmph = 10 ms-1.
Final velocity of larger fragment,
v1 = 25ms-1.
Initial velocity of smaller fragment,
u2 = 10ms-1.
Final velocity of smaller fragment,
v2 = – 12.5ms-1.
According to the law of conservation of momentum,
mu = m1v1 + m2v2
10 × 10 = x.25 + (10 – x) – 12.5
100 = 25x – 125 + 12.5x
225 = 37.5x
∴ x = \(\frac{225}{37.5}\) = 6Kg
∴ Mass of larger fragment, m1 =. 6kg
Mass of smaller fragment m2 = (10 – x) = 4kg.
![]()
Question 14.
A neutron (mass = 1.67 × 1o-27kg) at a speed of 108m s-1. Collides with detron and gets sticked to it Find the velocity of the composite particle.
Solution:
Mass of neutron 1.67 × 10-27 kg
= Mn,
mass of detron = (mn) = 3.34 × 10-27 kg
= md,
velocity of neutron = 108m s-1 = Vn
velocity of detron = 0 m s-1 = Vd
On collision,
mass of composite particle = Mc = Mn + Md
= (1.67 + 3.34) × 10-27 kg
= 6.01 × 10-27 kg
velocity of composite particle = vc
From Law of conservation of momentum
Mn + Vn + McVc = McVc
1.67 × 10-27 × 10+8 + 0 = (5.01 × 10-27) Vc
⇒ Vc = \(\left(\frac{1.67}{5.01}\right)\) × 10+8
Vc = 0.33 × 108m s-1
Question 15.
A projectile is fired a with velocity ‘V’ at an angle ‘θ’. If the projective breaks into 2 equal parts and one of them retraces the path then find the velocity of the other part
Solution:
At the highest point the projective will have only x-direction velocity and it is constant throughout the path.
S0, Vx = Vi cos θ
Let ‘M’ be the initial mass, \(\frac{M}{2}\) be mass of the halves. Velocity of 1 half changes from vx to – vx. Let the velocity of other half be V0. From Law of conservation of momentum.

⇒ V0 = 3 Vx
⇒ v0 = 3 vi cos θ.