KSEEB SSLC Class 10 Maths Solutions Chapter 5 Areas Related to Circles Ex 5.3 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 5 Areas Related to Circles Exercise 5.3.
Karnataka SSLC Class 10 Maths Solutions Chapter 5 Areas Related to Circles Exercise 5.3
{Unless stated otherwise, use \(\pi=\frac{22}{7}\)}
Question 1.
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
Solution:
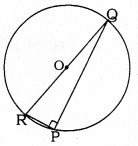
PQ = 24 cm, PR = 7 cm,
‘O’ is the centre of circle.
Angle in semicircle,
∠RPQ = 90°
In ⊥∆RPQ, ∠P = 90°
RQ = RP2 + PQ2
= (7)2 + (24)2
= 49 + 576
RQ2 = 625
∴ RQ = 25 cm.
Diameter, RQ = 25 cm.
∴ Radius, OR = OQ = \(\frac{25}{2}\) cm.
Area of shaded part :
= Area of semicircle – Area of ∆RPQ
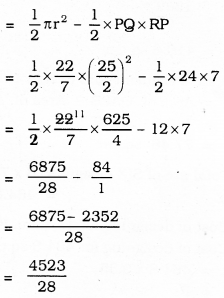
= 161.3 sq.cm.
Question 2.
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.
Solution:
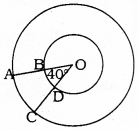
Radius of small circle, r = 7 cm
Radius of big circle, R = 14 cm
∠AOC = θ = 40°
Area of shaded part, ABCD =?
Area of ABCD
= Area of OAC – Area of OBD
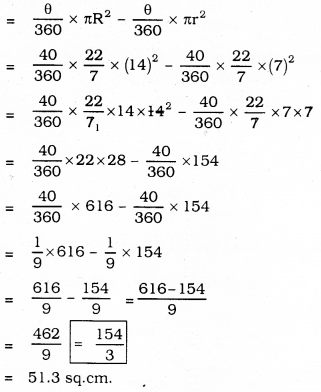
Question 3.
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
Solution:
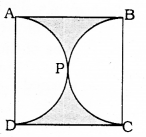
Each side of square ABCD = 14 cm.
APD, APC are semicircles.
Area of the shaded region = ?
i) Total area of square
= (Side)2
= (14)2
= 196 sq.cm.
ii) Each radius, r of semicircle
r = \(\frac{14}{2}\) =7cm
Area of two semicircles :
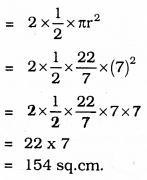
∴ Area of shaded region:
= Area of square – Area of two semicircles
= 196 – 154
= 42 sq. cm
Question 4.
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
Solution:
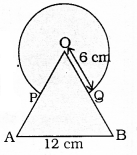
OAB is an equilateral Triangle with side 12 Circle with radius of 6
Each angle of an equilateral triangle is 60°
Angle at the centre in segment, θ = 60°
Area of Major segment + Area of an equilateral triangle OAB =
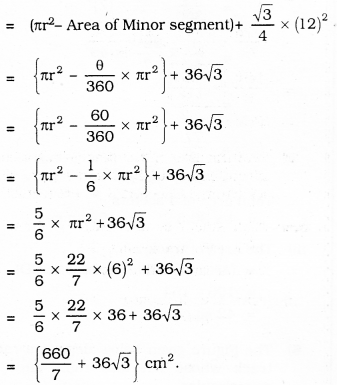
= 94.28 + 36 × 1.73
= 94.28 + 62.28
= 156.56 sq. cm.
Question 5.
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square.
Solution:
i) Each side of square ABCD = 4 cm.
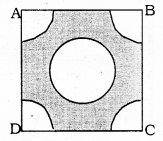
∴ Area of Square:
= (Side)2
= (4)2
= 16 sq.cm.
(ii) Area of circle in the corner A is 1 cm.
Radius, r = 1 cm.
θ = 90°
∴ Area of quadrant of circle:
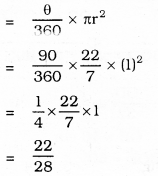
= 0.78 sq.cm.
iii) Radius of circle having diameter 2 cm, r = 1 cm.
∴ Area of circle:
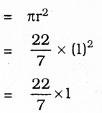
= 3.14 sq. cm.
∴ Area of remaining part of Square :
= Area of Square – Area of 4 quadrants – Area of Circle.
= 16 – 4 × 0.78 – 3.14
= 16 – 3.12 – 3.14
= 16 – 6.26
= 9.74 sq.cm.
Question 6.
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design.
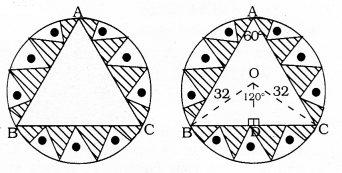
Solution:
Radius of the circle r = 32 cm.
∴ Area of the circle = πr2
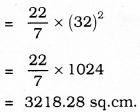
ii) ∠BAC = 60° ∴ ∠BOC = 120°
(∵ Angle at the centre is double than the angle in the circumference).
Now, in ∆OBC, BC ⊥ OD,
∠BOD = ∠COD = 60°

∴ ∆ABC is an equilateral triangle.
Each side of this triangle,
a= 2 × \(16 \sqrt{3}=32 \sqrt{3} \mathrm{cm}\)
Area of equilateral triangle, ∆ABC :
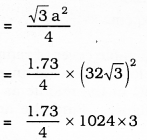
= 1328.64 sq.cm,
iii) Area of shaded region :
= Area of circle – Area of an equilateral ∆le
= 3218.28 – 1328.64
= 1889.6 sq.cm.
Question 7.
In the Figure given below, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
Solution:
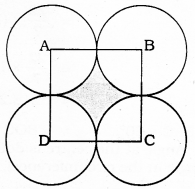
i) Each side of square ABCD =14 cm.
∴ Area of square ABCD
= (Side)2
= (14)2
= 196 sq.cm.
ii) Measure of radii of 4 circles, r = \(\frac{14}{2}=\) = 7 cm.
∵ Distance between tangents which touches circles externally,
d = R + r = 7 + 7 = 14 cm.
Area of segment with centre, A = ?
r = 7 cm, θ = 90°

∴ Total area of 4 sectors
= 4 × 38.5 = 154 sq.cm.
iii) The Area of track :
= (Area of GHIJ – Area of ABCD)
= 196 – 154
= 42 sq.cm.
Question 8.
The Figure given below depicts a racing track whose left and right ends are semicircular.

The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
i) The distance around the track along its inner edge,
ii) The area of the track.
Solution:

The distance around the track along its inner edge:
= AB + Arc BEC + CD + Area of Arc DFA
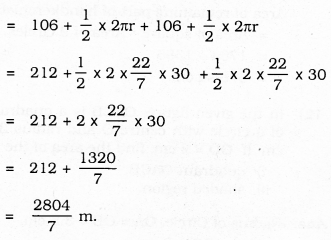
The Area of Track:
= (Area of GHIJ – Area of ABCD) + (Area of semicircle HKI – Area of semicircle BEC) + (Area of semicircle GIJ – Area of semicircle AFD)
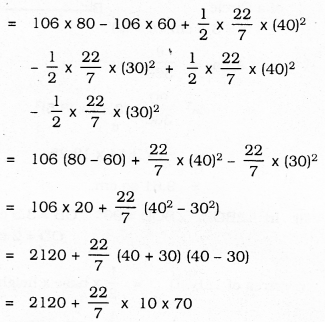
= 2120 + 2200
= 4320 sq.m.
∴ Total area of Track = 4320 sq.m.
Question 9.
In the figure given below, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Solution:
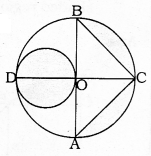
i) Radius of Big circle is the diameter of a small circle.
∴ Radius of small circle
= \(\frac{7}{2}\) = 3.5 cm
∴ Area of smalle circle = πr2
= \(\frac{22}{7}\) × (3.5)2
= \(\frac{22}{7}\) × 12.25
= 3.14 × 12.25
= 38.47 sq.cm.
ii) Area of segment OCB = ?
Radius, r = 7 cm, θ = 90°

∴ Area of sector OCB – Area of ∆OBC
= 38.47 – 24.50
= 13.97 sq.cm.
Similarly, Area of sector OAC – Area of ∆OAC
= 38.47 – 24.50
= 13.97 sq.cm.
∴ Total area of shaded region :
= Area of small circle + Area of Minor segment OBC + Area of Minor segment OAC
= 38.47 + 13.97 + 13.97
= 66.41 sq.cm.
Question 10.
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see the Figure). Find the area of the shaded region.
(Use π = 314 and \(\sqrt{3}\) = 1.73205).
Solution:
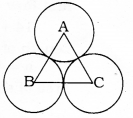
i) Area of an equilateral ∆ABC :
= 17320.5 cm2
\(\frac{\sqrt{3} a^{2}}{4}\) = 17320.5
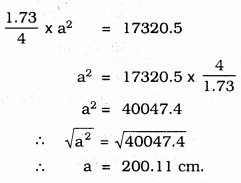
ii) Area formed by centre A:
r = 100 cm, θ = 60°

Similarly Area of sectors formed by centres B and C is 5233 sq.cm.
∴ Total Area of THREE sectors :
= 3 × 5233 = 15699 sq.cm.
∴ Area of the shaded region:
= Area of an equilateral Triangle – Area of three sectors.
= 17320.5 – 15699
= 1621.5 sq. cm.
Question 11.
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the Figure). Find the area of the remaining portion of the handkerchief.
Solution:
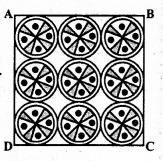
i) Total area of 9 circular designs each of radius 7 cm
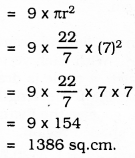
ii) All the circles touches externally.
∴ Sum of the diameter of 3 circles in first Row =
14 + 14 + 14 = 42 cm.
∴ Length of each side of square ABCD,
a = 42 cm.
∴ Area of square ABCD = a2
= (42)2
= 1764 sq.cm.
Area of remaining part of handkerchief:
= Area of a square – Area of 9 circles.
= 1764 – 1386
= 378 sq.cm.
Question 12.
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm If OD = 2 cm, find the area of the
i) quadrant OACB,
ii) shaded region.
Solution:
Radius of Circle, OA = OB = 3.5 cm.
OD = 2 cm.
i) Area of a quadrant of a circle
ii) Area of the shaded region
i) Area of quadrant (OACB) of a Circle
r = 3.5 cm, θ = 90°

ii) In ⊥∆BOD, ∠BOD = 90° OB = 3.5 cm; OD = 2 cm

∴ Area of shaded region,
= Area of quadrant OACB – Area of ABOD
= 9.61 – 3.5
= 6.11 sq.cm.
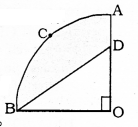
Question 13.
In Figure (i) given below, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
Solution:
i) Each side of square OABC = 20 cm.
∴ OA = 20 cm, AB = 20 cm.
∴ Area of square PABC = (Side)2
= (20)2
= 400 sq.cm.
ii) Diagonal OB is drawn in OABC square.
In ⊥∆OAB, OA = 20 cm.
AB = 20 cm.
OB =?
OB2 = OA2 + AB2
= (20)2 + (20)2
= 400 + 400
= 800

∴ Area of shaded region = 628 – 400 = 228 cm2.
Question 14.
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Figure given below). If ∠AOB = 30°, find the area of the shaded region.
Solution:
i) Area of segment OAPB = ?
r = 21 cm, θ = 30°
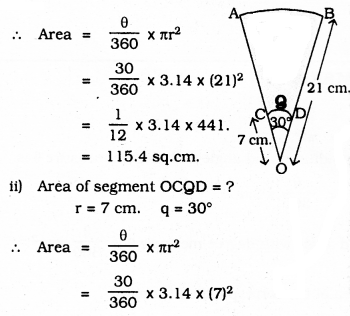
= \(\frac{1}{12}\) × 3.14 × 49
= 12.82 sq.cm.
∴ Area of the shaded region = Area of Sector OAPB – Area of segment OCQD
= 115.4 – 12.82
= 102.58 sq.cm.
Question 15.
In the given figure (i), ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
Solution:
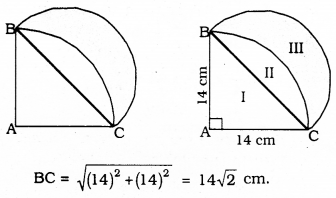
i) Area of Part II :
Area of Segment ABC – Area of ∆ABC
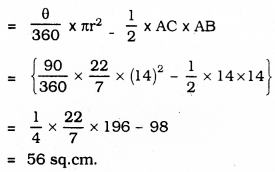
= 56 sq.cm.
ii) Area of shaded region Part III :
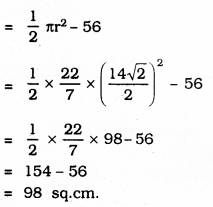
Question 16.
Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each
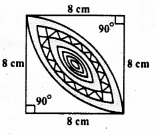
Solution:
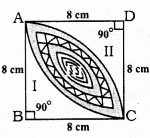
i) Area of Square, ABCD = a2 = (8)2 = 64 cm2.
ii) Sum of Areas of Part II and Part III = Area of the segment with centre D and radius of 8 cm.
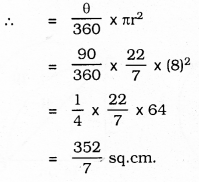
iii) Area of Part I = (Sum of Part I, II and III) – (Sum of the area of Part II, III)
= Area of Square ABCD – (Sum of the area of part II and III)

We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 5 Areas Related to Circles Ex 5.3 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 5 Areas Related to Circles Exercise 5.3, drop a comment below and we will get back to you at the earliest.