KSEEB SSLC Class 10 Maths Solutions Chapter 6 Constructions Ex 6.2

KSEEB SSLC Class 10 Maths Solutions Chapter 6 Constructions Ex 6.2 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 6 Constructions Exercise 6.2.

Karnataka SSLC Class 10 Maths Solutions Chapter 6 Constructions Exercise 6.2

In each of the following, give also the justification of the construction :
Question 1.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:
r = 6 cm,, d = 10 cm., t = ?

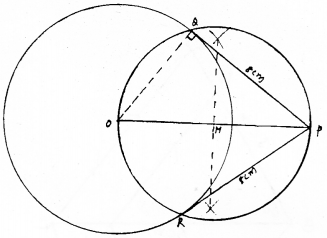
Tangent, PQ = PR = 8 cm.
Steps of Construction :

1. A circle with radius 6 cm is drawn taking O’ as centre.
2. Point P is marked at 10 cm apart from centre of circle.
3. With the half of compass mark M which is the mid-point of OP.
4. A circle is drawn at M taking radius MO or MP which intersect the given circle at Q and R.
5. Now join PQ from P, and Join PR, required tangents are obtained. If measured it is PQ = PR = 8 cm.

Question 2.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Solution:
Steps of Construction:

1. With ‘O’ as centre two circles are constructed with radii 4 cm and 6 cm.
2. Draw OM radius for small circle and drawn perpendicular at M which meets the big circle at P and Q.
3. Now PQ is the tangent drawn for a small circle.
   

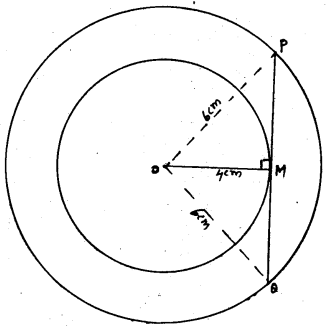
Tangent PMQ = 9 cm
Verification : In ⊥∆OMP, ∠M = 90°.
∴ OM² + PM² = OP²
(4)² + PM² = (6)²
PM² = (6)² – (4)² = 36 – 16
PM² = 20
∴ PM = \(\sqrt{20}\) = 4.5 cm.
Similarly,
MQ = 4.5 cm.
∴ PQ = PM + MQ = 4.5 + 4.5
∴ PQ = 9 cm.

Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution:
Draw Pw, Px tangents to circle with centre ‘O’ at P.
Draw Qy, Qz tangents to circle with centre ‘O” at Q.

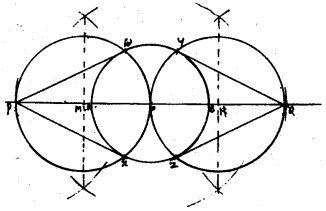
Tantent, OP = OQ = 7 cm.
Steps of Construction :

1. Construct a circle with radius 3 cm with centre O’. Draw the diameter AB and on both sides mark P and Q such that OP = OQ = 7 cm.
2. Bisect PO, Mark point M and draw circle of radius MO and centre M. It intersects given circle at w and x.
   If joined Pw and Px, required tangents are constructed.
3. Similarly, bisect OQ, mark point N. Draw a circle of radius NO or NQ with centre N, it meets given circle at y and z points. Join Qy and Qz. These are the required tangents.

Question 4.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution:
r = 5 cm.
Angle between tangents is 60°.

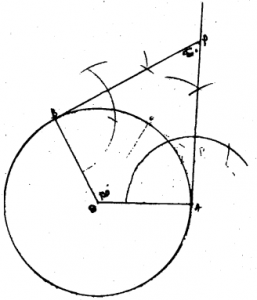
Steps of Construction :

1. A circle is drawn with centre ‘O’ and radius 5 cm. Draw OA and OB radii and ∠AOB = 120°
2. Tangents are drawn at A and B and these intersect at P.
3. By measurement, ∠APB = 60°.
   Angle between tangents PA and PB is 60°.
   ∵ ∠AOB and ∠APB Supplementary angles.

Question 5.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution:

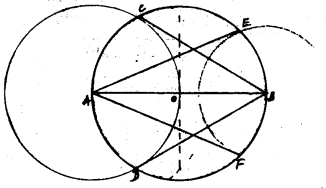
Steps of Construction :

1. Draw a line segment AB = 8 cm. Draw two circles with radii 4 cm and 3 cm at A and B.
2. To construct tangent from centre A to Centre B, it intersects at ‘O’ which is the midpoint of AB.
   Draw circle with radius OA, OB at Centre ‘O’, it intersects circle with centre A at C and D and with centre ‘B’ at E and F.
3. Now join E to A centre and F, required AE and AF tangents are constructed.
4. Similarly ‘B’ centre is joined to C and D, BC and BF tangents are constructed.
5. AE and AF are tangents drawn from centre ‘A’ to centre ‘B’.
   Tangents drawn from centre B to centre A are BC and BD.

Question 6.
Let ABC be a right triangle in which AB= 6 cm, BC = 8 cm and ∠B = 90°. BD is perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:
AB and AR are tangents drawn for circle with centre P from external point A.
Steps of Construction :

1. ⊥∆ ABC is constructed with BC = 8 cm. (base), ∠B = 90°, AB = 6 cm.
2. Draw BD ⊥ AC. , Draw perpendicular bisectors of DC and BC, they intersect at P.
3. A circle is drawn with centre P through A, B, D, and C.
   
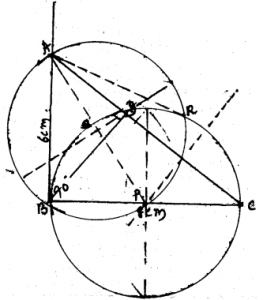
   For this circle AB and AR tangents are constructed from external point A.
   Tangent, AB = AR = 6 cm.

Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution:

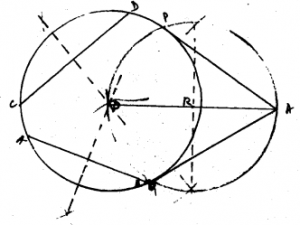
Steps of Construction:

1. Draw a circle with the help of a circular bangle kept on paper.
2. To draw AB and CD chords for this circle which has no centre. Their perpendicular bisectors meet at ‘O’. Now ‘O’ is the centre of the circle.
3. Mark point A on the outside of the circle from centre. Join OA. R is the midpoint of OA.
4. A circle is drawn with radius RO or RA which intersects the first circle at P and Q. Now join P from A and from A to Q, required two tangents AP and AQ are constructed.
   Tangent, AP = Tangent, AQ.

We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 6 Constructions Ex 6.2 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 6 Constructions Exercise 6.2, drop a comment below and we will get back to you at the earliest.