KSEEB SSLC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.3

KSEEB SSLC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.3 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.3.

Karnataka SSLC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.3

Question 1.
Find the area of the triangle whose vertices are:
i) (2, 3), (-1,0), (2,-4)
ii) (-5, -1), (3, -5), (5, 2)
Solution:
i) Let A (2, 3) = (x₁, y₁)
B (-1, 0) = (x₂, y₂)
C (2, -4) = (x₃, y₃).
Area of the triangle from the given data:

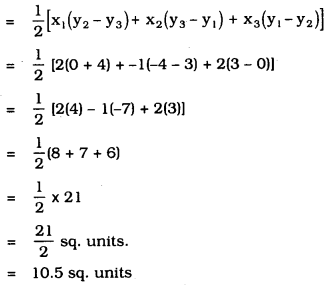
∴ Area of ∆ ABC = 10.5 sq. units

ii) Let A (-5, -1) = (x₁, y₁)
B (3, -5) = (x₂, y₂)
C (5, 2) = (x₃, y₃).
Area of the triangle from the given data :

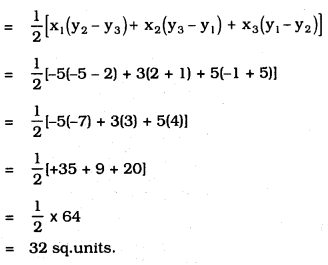
∴ Area of ∆ ABC =32 sq. units

Question 2.
In each of the following find the value of ‘k’, for which the points are collinear.
i) (7, -2), (5, 1), (3, k)
ii) (8, 1), (k, -4), (2, -5)
Solution:
i) Let A (7,-2)= (x₁, y₁)
B (5, 1) = (x₂, y₂)
C (3, k) = (x₃, y₃).
Points are collinear, therefore the area of the triangle formed by these is zero (0).

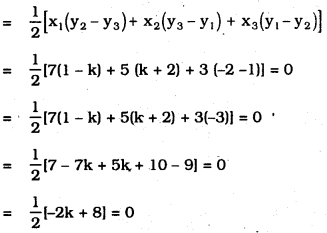
-k + 4 = 0
-k = -4
∴ k = 4

ii) Let A (8, 1) = (x₁, y₁)
B (k, -4) = (x₂, y₂)
C (2, -5) = (x₃, y₃).
Area of Triangle ABC = 0
∴ ABC is a straight line.

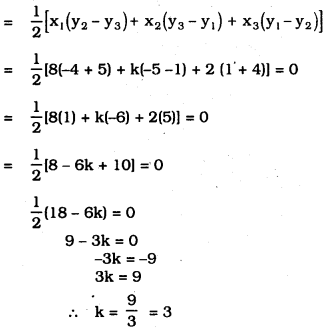
Question 3.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Solution:
Let the mid-points of ∆ABC are P, Q, R and also the mid-points of AB, BC and AC.

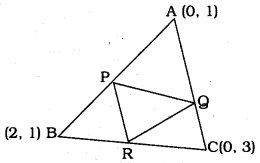
As per Mid-point formula,


\(=\frac{1}{2} \times \frac{1}{2}=\frac{1}{4}\)
Area of ∆PQR : Area of ∆ABC
∴ 1 : 4

Question 4.
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3)

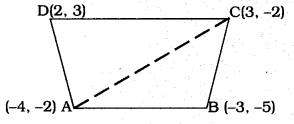
Solution:
Area of quadrilateral ABCD =?
In the quadrilateral ABCD, diagonal AC is drawn which divides ∆ABC, ∆ACD.
Sum of these triangles is equal to the Area of the quadrilateral.
i) Now, Area of ∆ABC :

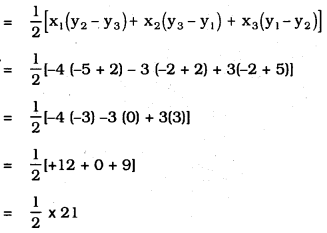
= 10.5 sq. units

ii) Area of ∆ACD

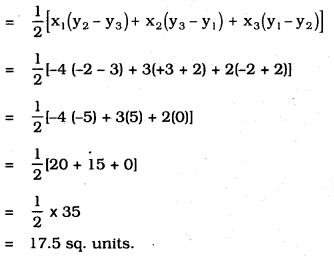
∴ Area of quadrilateral:
= Area of ∆ABC + Area of ∆ACD = 10.5 + 17.5 = 28 sq. units.
∴ Area of quadrilateral ABCD = 28 sq.units.

Question 5.
You have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ABC whose vertices are A(4, -6), B(3, -2) and C(5, 2).

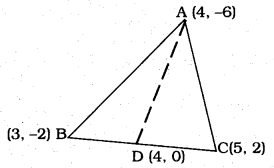
Solution:
AD Median is drawn to side BC which is the vertex of ∆ABC.
Median AD divides AABC into two triangles ∆ABD and ∆ADC which are equal in area.
Now Median AD bisects BC.
∴ BD = DC.
i) As per the Mid-Points formula,
Coordinates of D are
= \(\sqrt{(4)^{2},(0)^{2}}\)
= \(\sqrt{16,0}\)
= (4,0)
∴ Coordinates of D are (4, 0)

ii) Now, Area of ∆ABD:

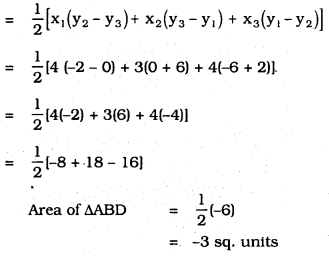
iiii) Now, Area of ADC:

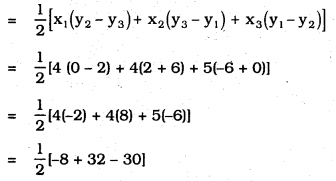
= \(\frac{1}{2}\) × -6
= – 3 sq. units.
∴ Area of ∆ADC = -3 sq. units.
∴ Area of ∆ABC :
= Area of ∆ABD + Area of ∆ADC
= (-3) +(-3)
= -6 sq. units.

iv) Now, Area of ∆ABC : (Direct Method)

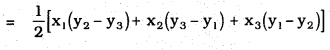
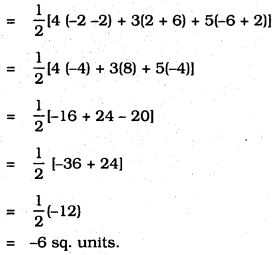
We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.3 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.3, drop a comment below and we will get back to you at the earliest