KSEEB SSLC Class 10 Maths Solutions Chapter 8 Real Numbers Ex 8.1 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 8 Real Numbers Exercise 8.1.
Karnataka SSLC Class 10 Maths Solutions Chapter 8 Real Numbers Exercise 8.1
Question 1.
Use Euclid’s division algorithm to find the HCF of:
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255
Solution:
(i) 135 and 225
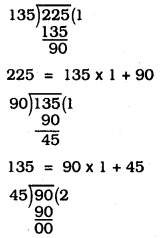
∴ 90 = 45 × 2 + 0
∴ HCF of 135 and 225 is 45.
(ii) 196 and 38220

∴ 38220 = 196 × 195 + 0
∴ HCF of 196 and 38220 is 196.
(iii) 867 and 2552
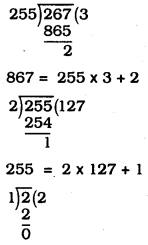
2 = 1 × 2 + 0
∴ HCF of 867 and 2552 is 1.
![]()
Question 2.
Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Solution:
Let us consider a positive odd integer as ‘a’.
On dividing ‘a’ by 6, let q be the quotient and ‘r’ be the remainder.
∴ Using Euclid’s lemma, we get a = 6q + r
where 0 ≤ r < 6 i.e., r = 0, 1, 2, 3, 4 or 5 i.e.,
a = 6q + 0 = 6q or a = 6q + 1
or a = 6q + 2 or a = 6q + 3
or a = 6q + 4 or a = 6q + 5
But, a = 6q, a = 6q + 2, a = 6q + 4 are even values of ‘a’.
[∵ 6q = 2(3q) = 2m1 6q + 2 = 2(3q + 1) = 2m2,
6q + 4 = 2(3 q + 2) = 2m3]
But ‘a’ being an odd integer, we have :
a = 6q + 1, or a = 6q + 3, or a = 6q + 5
Question 3.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march ?
Solution:
HCF of 32 and 616

∴ 32 = 8 × 4 + 0
∴ HCF of 32 and 616 is 8.
∴ Both groups can march in 8 columns.
Question 4.
Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
[Hint: Let x be any positive integer then it is of the form 3g, 3q + 1 or 3g + 2. Now square each of these and show that they can be rewritten in the form 3m or 3m +1.]
Solution:
Let us consider an arbitrary positive integer as ‘x’ such that it is of the form
3q, (3q + 1) or (3q + 2)
For x = 3q, we have x2 = (3q)2
⇒ x2 = 9q2 = 3(3q2) = 3m ………. (1)
Putting 3q2 = m, where m is an integer.
For x = 3q + 1,
x2 = (3q + 1)2 = 9q2 + 6q + 1
= 3(3q2 + 2q) + 1 = 3m + 1 ………… (2)
Putting 3q2 + 2q = m, where m is an integer.
For x = 3q + 2,
x2 = (3q + 2)2
= 9q2 + 12q + 4 = (9q2 + 12q + 3) + 1
= 3(3q2 + 4q + 1) + 1 = 3m + 1 ……….. (3)
Putting 3q2 + 4q +1 = m, where m is an integer.
From (1), (2) and (3),
x2 = 3m or 3m + 1
Thus, the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
![]()
Question 5.
Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Solution:
Let a and b be two positive integers and a > b
a = (b × q) + r where q and r are positive integers and 0 ≤ r < b.
Let b = 3 (if 9 is multiplied by 3 a perfect cube number is obtained)
a = 3q + r where 0 ≤ r < 3
(i) if r = 0, a = 3q
(ii) if r = 1, a = 3q + 1
(iii) if r = 2 a = 3q + 2
Consider cubes of these,
case i) a = 3q
a3 = (3q)3 = 27q3 = 9(3q3)
a3 = 9m
where m= 3q3 & m is an integer
case ii) a = 3q + 1
a3 = (3q + 1)3
(a + b)3 = a3 + b3 + 3a2b + 3ab2
a3 = 27q3 + 1 + 27q3 + 9q
a3 = 27 q3 + 27 q2 + 9q + 1
a3 = 9 (3q3 + 3q2 + q) + 1
a3 = 9m + 1
where m = 3q3 + 3q2 + q & m is an integer
case iii) a = 3q + 2
a3 = (3q + 2)3 = 27q3 + 8 + 54q2 + 36q
a3 = 27q3 + 54q2 + 36q + 8
= 9 (3q3 + 6q2 + 4q) + 8
a3 = 9m + 8
where m = 3q3 + 6q2 + 4q and m is an integer.
∴ Cube of any positive integer is either of the form 9m, 9m + 1 (or) 9m + 8 for some integer m.
We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 8 Real Numbers Ex 8.1 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 8 Real Numbers Exercise 8.1, drop a comment below and we will get back to you at the earliest