Students can Download 1st PUC Maths Model Question Paper 5 for Practice, Karnataka 1st PUC Maths Model Question Paper with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 1st PUC Maths Model Question Paper 5 for Practice
Time: 3 Hrs 15 Min
Max. Marks: 100
Instructions:
- The question paper has five parts namely A, B, C, D and E. Answer all the parts.
- Part-A carries 10 marks. Part-B carries 20 marks. Part-C carries 30 marks. Part-D carries 20 marks, Part-E carries 10 marks.
Part – A
I. Answer all the questions ( 1 × 10 = 10 )
Question 1.
If set A = {1, 3, 5}, then find the number of elements in P(A)1
Question 2.
Find the value of tan \(\frac{19 \pi}{3}\).
Question 3.
Express (5t)( \(-\frac{3}{5}\) i ) in the form a + ib,. where a, b ∈ R
Question 4.
If \(\frac{1}{6 !}+\frac{1}{7 !}=\frac{x}{8 !}\) find x.
![]()
Question 5.
Find the tenth term of G.P : 5, 25, 125, ……………..
Question 6.
Find the slope of the line \(\frac{x}{3}+\frac{y}{2}\) = 1.
Question 7.
Find the derivative of x2 – 2 at x = 0.
Question 8.
Write the contrapositive of “if a number is divisible by 9 then it is divisible by 3”.
Question 9.
Define mutually exclusive events.
Question 10.
If for some non empty sets A and B containing 3 elements A × B – {(3,4), (5, -3), (6,1)} . Find the set A.
![]()
Part – B
II. Answer any Ten questions ( 10 × 2 = 20 )
Question 11.
If A = {1, 2, 3, 4}, B = {2, 3, 5} and C = {3, 5, 6}, find A ∪ (B ∩C).
Question 12.
If X and Y are the two sets such that n(X) = 17, n(Y) 23 and n(X ∪ F) = 38. Find n(X ∩ Y)
Question 13.
Find the range and domain of the real function f(x) = \(\sqrt{9-x^{2}}\)
Question 14.
The minute hand of a clock is 2.1 cm long. How far does its tip move in 20 minute? ( use π = \(\frac{22}{7}\)
Question 15.
If sin A = \(\frac{3}{5}\) and A is in I quadrant, then find sin 2A.
Question 16.
Evaluate: \(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{x}\)
Question 17.
A die is thrown. Write the sample space. Also find the probability of the event “A number greater than or equal to 3 will appear”.
![]()
Question 18.
Write the component statement of the following compound statement and check whether the compound statement is true or false; “Zero is less than every positive integer and every negative integer “.
Question 19.
The co-efficient of variation and standard deviation are 60 and 21 respectively. What is the arithmetic mean of the distribution?
Question 20.
Find the equation of the line perpendicular to the line x + y + 2 = 0 and passing through the point (-1, 0).
Question 21.
Represent the complex number z = -1 + i in polar form.
Question 22.
Solve 3x + 2y > 6 graphically.
Question 23.
Find the distance between the parallel lines 3x – 4y + 7 = 0 and 3x – 4y + 5 = 0
Question 24.
Show that the points A(l, 2, 3), B(-l, – 2, -3), C(2, 3, 2) and D(4, 7, 6) are the vertices of a parallelogram.
Part – C
III. Answer any Ten questions ( 10 × 3 = 30 )
Question 25.
In a survey of 600 students in a school, 150 students were found to be taking tea and 225 taking coffee, 100 were taking both tea and coffee.
Find how many students were taking neither tea nor coffee?
Question 26.
Write the relationR defined as R = {(x,; x + 5):x∈ {0,1, 2, 3, 4}} in roster system. Write down its range and domain.
Question 27.
Provethat (cosx + cosy)2 + (sinx – siny)2 = 4cos2 \(\left(\frac{x+y}{2}\right)\)
![]()
Question 28.
Solve the equation x2 + 3x + 9 = 0.
Question 29.
Find the real 0 such that \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\) is purely real.
Question 30.
In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that
(i) The student has opted for NCC or NSS
(ii) The student has opted for NCC but not NSS
Question 31.
Find the coefficient of x6y3 in the expansion of (x + 2y)6
Question 32.
Find the sum of the sequence : 7, 77, 777, 7777…………….. to n terms.
Question 33.
Find the value of n so that \(\frac{a^{n+1}+b^{n+1}}{a^{n}+b^{n}}\) may be geometric mean between a and b.
![]()
Question 34.
Find the derivative of the function ‘sin x’ with respect to ‘x’ from first principle.
Question 35.
Find the center and radius of the circle 2x2 + 2y2 + 8x + 10y – 8 = 0
Question 36.
Find the number of different 8-letter arrangements that can be made from the letters of the word DAUGHTER so that
(i) all vowels occur together
(ii) all vowels do not occur together.
Question 37.
Verify by the method of contradiction that √2 is irrational,
Question 38.
Find the probability that when a hand of 7 cards is drawn from a well shuffled deck of 52 cards, it contains
(i) 3 kings
(ii) At least 3 kings.
Part – D
IV. Answer any Six questions ( 6 × 5 = 30 )
Question 39.
The real-valued function f is defined by
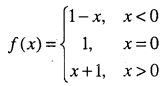
Draw the graph of f(x) and hence find the domain and range
Question 40.
Prove that lim \(\lim _{\theta \rightarrow 0}\left(\frac{\sin \theta}{\theta}\right)=1\) (θ being in radians) and hence show that \(\lim _{\theta \rightarrow 0}\left(\frac{\tan \theta}{\theta}\right)=1\)
![]()
Question 41.
Prove by mathematical induction that
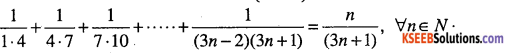
Question 42.
A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of:
(i) exactly 3 girls ?
(ii) atleast 3 girls ?
(iii) at most 3 girls ?
Question 43.
The second, third and fourth terms in the binomial expansion (x + a)n are 240, 720 and 1080, respectively. Find x, a and n.
Question 44.
Derive an expression for the coordinates of a point that divides the line joining the points A(x1, y1, z1) and B (x2, y2, z2) internally in the ratio m:n. Hence, find the coordinates of the midpoint of A body of mass where A(2, -3, 4) and B(-1, 2, 1).
Question 45.
Derive the equation of the line in the form x cos α + y sin α = p where p is the length of perpendicular from origin to straight line and α is the angle made by the perpendicular with positive direction of x axis. Using this find the equation of the straight line with p = 4 and α = 120°.
![]()
Question 46.
Prove that
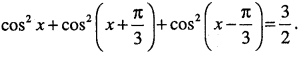
Question 47.
Solve the following linear inequalities 2x + y ≥ 6 and 3x + 4y ≤ 12 graphically.
Question 48.
Find the mean deviation about the median age for the age distribution of 100 persons given below:

Part – E
V. Answer any ONE question ( 1 × 10 = 10 )
Question 49.
(a) Prove geometrically that cos (x + y) = cos x cos y – sin x sin y using unit circle method and hence write the formula for cos (x – y). (6)
(b) Find the sum to n terms of the series: 1.2.3 + 2.3. 4 + 3.4.5 …………………… (4)
![]()
Question 50.
(a) Define Hyperbola as a set of points and
Derive its equation in the form \(\frac{x^{2}}{a^{2}}-\frac{x^{2}}{a^{2}}=1\)
(b)
![]()
Karnataka 1st PUC Maths Model Question Paper 1 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 100
Instructions:
- The question paper has five parts namely A, B, C, D and E. Answer all the parts.
- Part-A carries 10 marks. Part-B carries 20 marks. Part-C carries 30 marks. Part-D carries 20 marks, Part-E carries 10 marks.
Part – A
I. Answer all the questions: ( 10 × 1 =10 )
Question 1.
If A= {1,2}, B = {x : x ∈ A and x2 – 9 = 0}. Find A x B.
Question 2.
Define subset of a set.
Question 3.
Convert \(\frac{2 \pi}{3}\) radians into degree measure
Question 4.
Express \(\frac{5+i \sqrt{2}}{2 i}\) in the form x + iy.
Question 5.
Find n if (n – l)p3: np4 = 1: 9
![]()
Question 6.
Find the tenth term of G.P : 5, 25, 125………….
Question 7.
Find the slope of the line joining the points (3, -2) and (-1,4).
Question 8.
Evaluate: \(\lim _{x \rightarrow 0}\left(\frac{\cos x}{\pi-x}\right)\)
Question 9.
Write the contrapositive of “if a number is divisible by 9 then it is divisible by 3”.
Question 10.
Write the sample space for the experiment “a.coin is tossed repeatedly three times”.
![]()
Part – B
II. Answer Any Ten Questions ( 10 x 2 = 20 )
Question 11.
If the universal set U = { 1, 2, 3, 4, 5, 6, 7 } A = { 1, 2, 5, 7 } , B = { 3,4, 5, 6}. Verify (A ∪ B)’= A’ ∩ B’
Question 12.
In a class of 35 students, 24 likes to play cricket, 5 likes to play both cricket and football. Find how many students like to play football?
Question 13.
If A = { 1,2,3 }, B = { 3,4 },C={ 4,5,6 }. Find A x (B∪C).
Question 14.
A wheel makes 360 revolutions in one minute, through how many radians does it turn in one second ?
Question 15.
Find the value of (sin(15°))
Question 16.
Find the value of x and y, if (x + 2y) + i(2x – 3y) is the conjugate of 5 + 4i.
Question 17.
Solve 7x +1 ≤ 4x + 5 and represent the solution graphically on the number line.
Question 18.
Find the equation of the line passing through (-1, 1) and (2, -4)
![]()
Question 19.
Find the equation of the line passing through (-4, 3) with slope ( \(\frac{1}{2}\) )
Question 20.
Find the ratio in which the line segment joining the points (4, 8,10) and (6,10, -8) is divided by YZ-Plane.
Question 21.
Evaluate : \(\lim _{x \rightarrow 0} \frac{1-\cos x}{x}\)
Question 22.
Write the component statement of the following compound statement and check whether the compound statement is true or false; “ Zero is less than every positive integer and every negative integer”.
Question 23.
The co-efficient of variation and standard deviation are 60 and 21 respectively. What is the arithmetic mean of the distribution.
Question 24. One card is drawn from a well-shuffled deck of 52 cards. Calculate the probability that the card will be “not an ace”.
![]()
Part – C
III. Answer Any Ten Questions ( 10 x 3 = 30 )
Question 25. Let A = {1, 2, 3, 14} Define a relation R from A to A by R = {(.x, y): 3x -y = 0, x, y ∈ A} write its domain
and range.
Question 26.
Find the general solution of 2 cos2 x + 3 sin x = 0.
Question 27.
Express √3 + i in the polar form.
![]()
Question 28.
Solve: 3x2 – 4x + \(\frac{20}{3}\) = 0
Question 29.
How many numbers greater than 10,00000 can be formed by using the digits 1, 2, 0, 2, 4, 2, 4.
Question 30.
Using the Binomial theorem, which number is among (1.1)10000 and 1000.
Question 31.
In an A.P, if mth term is n and nth term is m. Then find pth term (m # n).
Question 32.
Find the sum of n terms of an A.P whose kth term is (5k + 1).
Question 33.
Find the co-ordinates of the foci and latus rectum of the hyperbola 3x2 – y2 = 3.
Question 34.
Find the derivative of sin x from first principle.
Question 35.
Given p : 25 is a multiple of 5 : q: 25 is a multiple of 8. Write the compound statement connecting these two statements with “and”, “or”. In 60th cases check the validity of the statement.
Question 36.
The student Anil and Ashima appeared in the examination, the probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination 0.10. The probability that the both will qualify the examination is 0.02. Find the probability that only one of them qualify the examination.
Question 37.
A letter is chosen at random from the ward ‘ASSASSINATION’, Find the probability that the letter is (i) an vowel (ii) consonant.
![]()
Question 38.
In a survey of 600 students in a school, 150 students were found to be taking tea and 250 taking coffee, 100 were taking both tea and coffee. Find how many student were taking neither tea nor coffee.
Part -D
IV. Answer any Six questions ( 6 x 5 = 30 )
Question 39.
Define a polynomial function. If the function from f: R → R is defined as f(x) = x2 then draw the graph of/ and find the domain and range.
Question 40.
Prove that
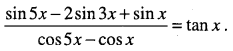
Question 41.
Prove by mathematical induction that 13 + 23 + …………….n3 = \(\left[\frac{n(n+1)}{2}\right]^{2}\)
Question 42.
Solve graphically 2x + y ≥ 4,x + y ≤ 3, 2x – 3y ≤ 6
Question 43.
A group consists of 4 girls and 7 boys, In how many ways can a team of 5 members be selected if the team has
(i) No girl
(ii) At least one boy and one girl
(iii) At least three girls
Question 44.
State and prove Binomial theorem for all natural numbers.
![]()
Question 45.
Derive the formula for the angle between two straight lines with slopes m1 and m2 hence find the slope of the line which makes an angle \(\frac{\pi}{4}\) with the line x – 2y + 5.
Question 46.
Derive the formula for the distance between two points x – 2y + 5 and x – 2y + 5 And hence find the distance between (2, -1, 3) and (-2, 1, 3).
Question 47. Prove geometrically: \(\lim _{\theta \rightarrow 0} \frac{\sin \theta}{\theta}=1\) where θ is in radian and hence deduce that \(\lim _{\theta \rightarrow 0} \frac{\tan \theta}{\theta}=1\)
Question 48.
Find the mean deviation about the mean for the following data

Part – E
V .Answer any ONE ( 1 x 10 = 10 )
Question 49.
a) Prove geometrically that cos (x + y) = cos x cos y – sin x. sin y and hence prove that cos (x – y) = cos x. cos y + sin x. sin y. 6
b) Find the sum of first n terms of the series 12 + 22 + …. + n2.
![]()
Question 50.
a) Define ellipse and derive the equation of the ellipse in standard form as \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 (a > b)
b) Find the derivation of \(\frac{x^{5}-\cos x}{\sin x}\) with respect to x.
Karnataka 1st PUC Maths Model Question Paper 2 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 100
Instructions:
- The question paper has five parts namely A, B, C, D and E. Answer all the parts.
- Part-A carries 10 marks. Part-B carries 20 marks. Part-C carries 30 marks. Part-D carries 20 marks, Part-E carries 10 marks.
Part – A
I. Answer all the questions: ( 10 × 1 =10 )
Question 1.
Define an empty set.
Question 2.
If ( \(\frac{x+1}{2}\) ,7 ) find ‘x’
Question 3.
Convert ( \(\frac{7 \pi}{6}\) ) into degrees .
Question 4.
Find the real number x if (x – 2i) (1 + i) is purely imaginary.
Question 5.
Given 5 flags of different colours how many different signals can be made if each signal requires the use of 2 flags, one below the other .
Question 6.
For what value of x the numbers \(\frac{-2}{7}\), x, \(\frac{-7}{2}\) are in G. P.
![]()
Question 7.
Find the slope of the line \(\frac{x}{3}+\frac{y}{2}\) = 1
Question 8.
Find the derivative of x2 – 2 at x = 0 .
Question 9.
Write the negation of ‘For all a, b ∈ I, a – b∈ I’.
Question 10.
Define sure event.
Part – B
II. Answer any Ten questions ( 10 × 2 = 20 )
Question 11.
In a school, there are 20 teachers who teach mathematics or physics. Of these 12 teach mathematics and 4 teach both physics and mathematics. How many teach physics?
Question 12.
If A ={1,2}, form the set A × A × A.
Question 13.
Taking the set of natural numbers as the universal set. If A = {x: x ∈ N, and 2x +1 > 10} and B = {x : x ∈ N, and 3x – 1 > 8 find A’ and B’.
Question 14.
Find the value of cos (- 1710°).
Question 15.
Prove that sin 2x = \(\frac{2 \tan x}{1+\tan ^{2} x}\)
Question 16.
Find the least positive integer m such that \(\left(\frac{1+i}{1-i}\right)^{4 m}\) =1
Question 17.
Solve {3 (2x-5 ) -7} ≥ 9(x-5).
Question 18.
Find the distance of a point (3,-5) from the line 3x – 4y – 5 =0.
Question 19.
Find the angle between the lines y – y√3 x – 5 = 0 and √3 y – x + 6 = 0.
![]()
Question 20.
Evaluate \(\lim _{x \rightarrow-2} \frac{\frac{2}{x}+\frac{1}{2}}{x+2}\) .
Question 21.
Show that the points P(-2, 3, 5), Q (1, 2, 3) and R (7,0,-1) are collinear.
Question 22.
Write the converse and contrapositive of ‘If a parallelogram is a square, then it is a rhombus’.
Question 23.
Write the mean of the given data 6,7,10,12,13,4,6,12 .
Question 24.
Given P(A) = \(\frac{3}{5}\) and P (B) = \(\frac{1}{5}\) find P (A or B)
Part – C
III. Answer any Ten questions ( 10 × 3 = 30 )
Question 25.
There are 200 individuals with a skin disorder. 120 has been exposed to the chemical A, 50 to chemical B and 30 to both chemical A and B. Find the number of individuals exposed to
(i) chemical A but not to chemical B
(ii) Chemical A or chemical B.
Question 26.
Let A = {1, 2}, B = {1, 2, 3, 4}, and C = {5, 6}. Verify that A × (B ∩C) = (A × B) ∩ (A × C)
sin A sin B sin C
Question 27.
Prove that in any triangle ABC, \(\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}\)
Question 28.
Express \(\frac{-1+i}{\sqrt{2}}\) in the polar form.
![]()
Question 29.
Solve the equation x2 + \(\frac{x}{\sqrt{2}}\) + 2 = 0
Question 30.
In how many ways can 5 girls and 3 boys be seated in a row so that no two boys are together.
Question 31.
Find the middle term in the expansion of \(\left(\frac{x}{3}+9 y\right)^{10}\)
Question 32.
The number of bacteria in a certain time double every hour. If there are 30 bacteria present in the culture originally. How many bacteria will be present at the end of 2nd hour, 4th hour, and nth hour.
Question 33.
The difference between any two consecutive interior angles of a polygon is 5°. If the smallest angle is 120°. Find the number of sides of the polygon.
Question 34.
Find the equation of the ellipse whose center at origin, major axis on the X axis and passes through the point (4, 3) and (6, 2).
Question 35.
Find the derivative of tan x w. r. t x from first principle.
Question 36.
Verify by the method of contradiction that √2 is irrational
Question 37.
One card is drawn from a well shuffled deck of 52 cards. If each outcome is equally likely, calculate the probability that the card will be
(i) diamond
(ii) not an ace
(iii) a black card.
Question 38.
A fair coin 1 marked on one face and 6 on the other and a fair die are both tossed. Find the probability that the sum of numbers that turn up is (i) 3 (ii) 12.
![]()
Part – D
IV. Answer any Six questions ( 6 × 5 = 30 )
Question 39.
Define modulus function. Draw the graph of modulus function, Write down its domain and range.
Question 40.
Prove that cos2 2x – cos2 6x = sin 4x . sin 8x
Question 41.
Prove by mathematical induction that
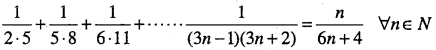
Question 42.
Solve the following system of inequalities graphically: 5x + 4y ≤ 40, x ≥ 2, y ≥ 3;
Question 43.
What is the number of ways choosing four cards from a pack of 52 playing cards. In how many of these
(i) Four cards of the same suit
(ii) are face cards
(iii) two red and two black card
(iv) cards are of the same colour.
Question 44.
For all real numbers a, b and positive integer V prove that,
(a + b)n = nC0an + nC1 an-1b + nC2 an-2b2 + …………….+nCn-1 abn-1 + nCnbn
Hence prove that C2 + C2 + C2 + ………….Cn = 2n
![]()
Question 45.
Derive a formula for the perpendicular distance of a point (x1, y1) from the line Ax + By + C = 0.
Question 46.
Derive the section formula in 3-D for internal division. Also find the coordinates of the midpoint of the line joining the points A (1,-2,3) and B (3,4,8).
Question 47.
Prove that \(\lim _{\theta \rightarrow 0} \frac{\sin x}{x}\) = 1 (x being in radians) and hence evaluate \(\lim _{x \rightarrow 0} \frac{\sin a x}{\sin b x}\)
Question 48.
The mean and standard deviation of 20 observations are found to be 10 and 2 respectively. On rechecking it was found that on observation 8 was incorrect. Calculate the correct mean and the standard deviation in each of the following cases
(i) if wrong item is omitted
(ii) if it is replaced by 12
![]()
Part – E
V. Answer any One question ( 1 × 10 = 10 )
Question 49.
(a) Prove geometrically that cos(A + B) = cos A cos S-sin A sin B
(b) Find the derivative of f(x) = 2x2 + 3x – 5, also prove that F'(0) + 3f'(-1) = 0
Question 50.
(a) Define parabola as a set of all points in the plane and derive its equation in the form y2 = 4ax, a > 0 and hence also find the focus and vertex.
(b) Find the sum to ‘n’ terms of the series 12 + (12 + 22) + (12 + 22 + 32) + …………..
Karnataka 1st PUC Maths Model Question Paper 3 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 100
Instructions:
- The question paper has five parts namely A, B, C, D and E. Answer all the parts.
- Part-A carries 10 marks. Part-B carries 20 marks. Part-C carries 30 marks. Part-D carries 20 marks, Part-E carries 10 marks.
Part – A
I. Answer all the questions ( 1 × 10 = 10 )
Question 1.
Write the set {x : x e R and – 4 < x ≤ 6} as an interval.
Question 2.
IfA = {1,2}, B = {3,4) then show that A x (B ∩ Φ) = Φ
Question 3.
If cos x = -3/5, x lies in the HI quadrant then find the value of sin x.
Question 4.
Evaluate: \(i^{24}+\left(\frac{1}{i}\right)^{26}\)
Question 5.
Find the number of 4 digits that can be formed using the digits 1, 2, 3, 4, 5. If no digit is repeated.
![]()
Question 6.
Which term of 2, 2√2, 4 is 128.
Question 7.
Reduce 6x + 3y – 5 = 0 into slope-intercept form.
Question 8.
Find \(\lim _{x \rightarrow 5}|x|-5\)
Question 9.
Write the negation of “Every natural number is greater than zero”.
Question 10.
If \(\frac{2}{11}\) is the probability of an event A then what is the probability of the event ‘not A’?
Part – B
II. Answer any ten questions ( 2 × 10 = 20 )
Question 11.
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2,4, 6, 8} and B = {2, 3, 5, 7} verify (A ∩B)’ = A’ ∪ B’.
Question 12.
If X and Y are two sets such that X ∪ Y has 50 elements, X has 28 elements and Y has 32 elements. How many elements does X ∩ Y have?
Question 13.
If A = {1, 2} and B = {3, 4} write A × B. How many subsets will A × B have?
Question 14.
The minute hand of a clock is 1.5 cm long. How far does its tip move in 40 Minute? (Use π = 3.142)
Question 15.
Prove that sin 3x = 3 sin x – 4 sin3x.
Question 16.
If x + iy = \(\frac{p+i q}{p-i q}\) prove that x2 + y2 = 1.
![]()
Question 17.
Solve the inequality (2x – 5) > (1 – 5x) and represent the solution graphically on the number line.
Question 18.
By using the concept of equation of the line prove that the three points (3, 0), (-2, -2) and (8, 2) are collinear.
Question 19.
Find the equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through the point (-2, 3).
Question 20.
Find the ratio in which the YZ-plane divides the line segment formed by joining the points (-2, 4, 7) and (3, -5, 8).
Question 21.
Compute the derivative of sin2 x.
Question 22.
By giving a counter example, show that the following statements is false: “If n is an odd integer then n is a prime”.
Question 23.
The mean and variance of heights of XI students are 162.6cm and 127.69cm2 respectively. Find the C.V.
Question 24.
A card is selected from a pack of 52 parts calculate the probability that the card is (i) an Ace (ii) a black card.
![]()
Part – C
III. Answer Any Ten Questions ( 3 x 10 = 30 )
Question 25.
In a survey of 400 students in a school, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple and orange juices. Find how many students were taking neither apple juice nor orange juice.
Question 26.
If f(x) = x2 and g(x) = 2x + 1 be two real functions find (i) (f + g) (x) (ii) (f – g) (x) (iii) (fg) (x)
Question 27.
Find the general solution of sec22x = 1 – tan2x.
Question 28.
Express \(\frac{1-i}{1+i}\) into polar form
![]()
Question 29.
Solve: 2x2 + √3x – 1 = 0
Question 30.
If 5.4Pr = 6.5Pr-1, then find r.
Question 31.
Find the coefficient of x5 of (x + 3 )8.
Question 32.
Insert five number between 8 and 26 such that resulting sequence is an A.P.
Question 33.
The sum of first three terms of a G.P. is \(\frac{13}{12}\) and their product if -1. Find the common ratio and the terms.
Question 34.
Find the equation of parabola with vertex at the origin, axis along x-axis and passing through the point (2, 3) also find its focus.
Question 35.
Differentiate \(\frac{x+1}{x}\) from first principle
Part – D
IV. Answer any six questions ( 5 × 6 = 30 )
Question 36.
Verify by the method of contradiction that √7 is irrational.
Question 37.
A bag contains 9 discs of which 4 are red 3 are blue and 2 are yellow. The discs are similar in shape and size.
The disc is drawn at random from the bag. Calculate the probability that will be ’
(i) red
(ii) no blue
(iii) either red or blue.
Question 38.
A and B are events such that P(A) = \(\frac{1}{4}\), P(B) = \(\frac{1}{2}\) and P(A and B) = \(\frac{1}{8}\). Find
(i) P(A or B)
(ii) P(not A and not B)
![]()
Question 39.
Define Signum function. Draw the graph of it and write down it Domain and Range.
Question 40.
Prove that cos2x cos \(\frac{x}{2}\) – cos3x cos \(\frac{9x}{2}\) = sin5x sin \(\frac{5x}{2}\)
Question 41.
Prove that 102n-1 + 1 is divisible by 11, ∀ n ∈ N by the principle of mathematical Induction.
Question 42.
Solve the following system of linear inequalities graphically. x + y ≥ 5, x – y ≤ 3.
Question 43.
Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls. If each selection consists of 3 balls of each colour.
Question 44.
Prove Binomial Theorem for positive integers with real numbers. Hence prove that
nC0 + nC2 + nC4+ …………………. = nC1 + nC3 + nC5 + ………………..
Question 45.
P(a. b) is the midpoint of the line segment between axes. Show that the equation of the line is \(\frac{x}{a}+\frac{y}{b}=2\)
Question 46.
Derive the formulae for distance between two points (x1, y1, z1) and I(x1, y2, z2) and hence find the distance between P(1, -3, 4) and Q(-4, 1,2).
![]()
Question 47.
Prove that \(\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\) where x is in radian and hence evaluate: \(\lim _{x \rightarrow 0} \frac{\sin 4 x}{\sin 2 x}\)
Question 48.
The mean and standard deviation of 100 observations were evaluated as 40 and 5.1 respectively. By a student who took by mistake, 50 instead of 40 for one observation. What are correct mean and standard deviation?
Part – E
V. Answer Any One Question: ( 1 × 10 = 10 )
Question 49.
a) Define ellipse as a set of all points in the plane and derive its equation in the standard form as \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
a > b
b) Find the derivate \(\frac{2}{x+1}-\frac{x^{2}}{3 x-1}\)
![]()
Question 50.
a) Prove geometrically that cos(x+y) = cosxcosy-sinxsiny and hence show that cos ( \(\frac{\pi}{2}\) + x) = – sin x.
b) Find the sum to n terms of series:
\(\frac{1}{1.2}+\frac{1}{2.3}+\ldots \ldots \ldots \ldots\)
Karnataka 1st PUC Maths Model Question Paper 4 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 100
Instructions:
- The question paper has five parts namely A, B, C, D and E. Answer all the parts.
- Part-A carries 10 marks. Part-B carries 20 marks. Part-C carries 30 marks. Part-D carries 20 marks, Part-E carries 10 marks.
Part – A
I. Answer all the questions ( 1 × 10 = 10 )
Question 1.
If A has 4 elements. How many subsets does A has?
Question 2.
Convert 520° in to radian measure.
Question 3.
Find the conjugate of √3i -1
Question 4.
If \(\frac{1}{6 !}+\frac{1}{7 !}=\frac{x}{8 !}\) then find x
Question 5.
Find the 20th term of the G.P. \(\frac{5}{2}, \frac{5}{4}, \frac{5}{8}, \cdots \cdots \cdots \cdots\)
Question 6.
Find the slope of the line making inclination of 60° with positive direction of x-axis.
![]()
Question 7.
Find the derivative of 2 × – \(\frac{3}{4}\)
Question 8.
Write the negation of ‘For all a, b ∈ I, a – b ∈ I’.
Question 9.
Define mutually exclusive events.
Question 10.
If for some non empty sets A and B containing 3 elements A × B = {(3,4), (5,-3), (6,1)}. Find the set A.
Part – B
II. Answer any Ten questions ( 10 × 2 = 20 )
Question 11.
If A = {1,2, 3, 4}, B = {2, 3, 5} and C = {3, 5, 6}, find A ∪ (b ∩ C).
Question 12.
If X and Y are the two sets such that n (X) = 17, n (Y) = 23 and n (X∪ Y) = 38. Find n (X ∩ Y).
Question 13.
Find the range and domain of the real function f(x) = \(\sqrt{9-x^{2}}\)
Question 14.
The minute hand of a clock is 2.1 cm long. How far does its tip move in 20 minute? ( use π = \(\frac{22}{7}\) )
tan A:-tan y
Question 15.
Prove that tan(x – y) = \(\frac{\tan x-\tan y}{1+\tan x \tan y}\)
![]()
Question 16.
Evaluate:
\(\lim _{x \rightarrow-1}\left[1+x+x^{2}+x^{2}+\cdots \cdots x^{10}\right]\)
Question 17.
A die is thrown. Write the sample space. Also find the probability of the event “A number greater than or equal to 3 will appear”.
Question 18.
Write the converse and contrapositive of ‘If a parallelogram is a square, then it is a rhombus’.
Question 19.
Two series A and B with equal means have standard deviations 9 and 10 respectively. Which series is more consistent?
Question 20.
Find the equation of the line perpendicular to the line x + y + 2 = 0 and passing through the point (-1, 0).
Question 21.
Represent the complex number z = -1 +i in polar form.
Question 22.
Solve 3x + 2y > 6 graphically.
Question 23.
Find the distance between the parallel lines 3x – 4y + 7 = 0 and 3x – 4y + 5 = 0.
![]()
Question 24.
Show that the points A(1, 2, 3), B(-1, -2, -3), C(2, 3, 2) and D(4, 7, 6) are the vertices of a parallelogram.
Part – C
III. Answer any TEN questions ( 10 × 3 = 30 )
Question 25.
In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis? How many like tennis only and not cricket?
Question 26.
Write the relation R defined as R = {(x,x + 5)}: x ∈ {0,1,2,3,4} in roster system. Write down its range and domain.
Question 27.
Prove that (cosx + cosy)2 + (sinx – sin y)2 =4cos2 ( \(\frac{x+y}{2}\) )
Questioin 28.
Solve the equation x2 + 3x + 9 = 0.
Question 29.
Find the real θ such that \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\) is purely real.
Question 30.
In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that (i) the student has opted for NCC or NSS (ii) The student has opted for NCC but not NSS.
Question 31.
Find the coefficient of x6y3 in the expansion of (x + 2y)6
Question 32.
Find the sum of the sequence : 7,77,777,7777, ……………….
Question 33.
In If \(\frac{a^{n}+b^{n}}{a^{n-1}+b^{n-1}}\) is the A.M. between a and b, then find the value of n.
Question 34.
Find the derivative of the function ‘-x’ with respect to ‘x’ from first principle.
![]()
Question 35.
Find the centre and radius of the circle x2 + y2 + 8x + 10y – 8 = 0.
Question 36.
How many words with or without meaning can be made from the letters of the word MONDAY assuming that no letter is repeated, if (i) 4 letters are used at a time, (ii) All letters are used at a time (iii) All letters are used but first letters a vowel.
Question 37.
Verify by the method of contradiction that √2 is irrational.
Question 38.
Find the probability that when a hand of 7 cards is drawn from a well shuffled deck of 52 cards, it contains (i) 3 kings (ii) At least 3 kings.
![]()
Part – D
IV. Answer any Six questions ( 6 × 5 = 30 )
Question 39.
Define greatest integer function. Draw the graph of greatest integer function, Write the domain and range of the function.
Question 40.
Prove that \(\lim _{\theta \rightarrow 0}\left(\frac{\sin \theta}{\theta}\right)=1\) (0 being in radians) and hence show that \(\lim _{\theta \rightarrow 0}\left(\frac{\tan \theta}{\theta}\right)=1\)
Question 41.
Prove by mathematical induction that
![]()
Question 42.
How many words with or without meaning each of 3 vowels and 2 consonants can be formed from the letters of the word INVOLUTE?
![]()
Question 43.
Find “a” if 17th and 18th terms of the expansion (2 + a)50 are equal.
Question 44.
Derive an expression for the coordinates of a point that divides the line joining the points A(x1, y1, z1) and B(x2, y2, z2) internally in the ratio m : n. Hence, find the coordinates of the midpoint of AB where A(2,-3,4) and B(-1,2,1)
Question 45.
Derive the equation of the line with slope m and y-intercept c. Also find the equation of the line for which tan θ = \(\frac{1}{2}\) and y-intercept is \(\frac{-3}{2}\)
Question 46.
Prove that
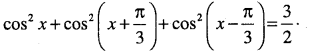
![]()
Question 47.
A manufacture has 600 Utters of a 12% solution of acid. How many liters of a 30% acid solution must be added to it so that the acid content in the resulting mixture be more that 15% but less than 18%.
Question 48.
Find the mean deviation about the median age for the age distribution of 100 persons given below

Part – E
V. Answer any One question ( 1 × 10 = 10 )
Question 49.
(a) Prove geometrically that cos(x + y) = cosx cosy – sinx siny using unit circle method and hence find the value of cos ( \(\frac{\pi}{2}\) + x ) = – sin x. (6)
(b) Find the sum to n terms of the series: 1.2.3 + 2.3.4 + 3.4.5 …………….. (4)
![]()
Question 50.
(a) Define Hyperbola as a set of points. Derive its equation in the form \(\frac{x^{2}}{a^{2}}-\frac{x^{2}}{a^{2}}=1\)
(b) Suppose
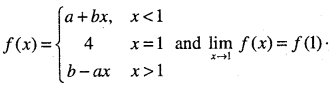
What are the possible values of a and b?