Students can Download Maths Chapter 16 Probability Questions and Answers, Notes Pdf, 1st PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 1st PUC Maths Question Bank Chapter 16 Probability
Question 1.
Name the mathematician who developed the theory of probability in 1933.
Answer:
Theory of probability was developed by Russian mathematician A.N. Kolmogorv in 1933.
Question 2.
Define the following terms:
(i) Random experiment
(ii) Outcomes
(iii) Sample space
(iv) Sample point.
Answer:
(i) Random experiment: An experiment is called random experiment if it has more than one possible outcome and it is not possible to predicts the outcome in advance. .
(ii) Outcomes: A possible result of a random experiment is called its outcome.
(iii) Sample space: The set of all possible outcomes of a random experiment is called the sample space associated with the experiment. It is denoted by the symbol S.
(iv) Sample point: Each element of a sample space is called sample point, or each outcome of the random experiment is called sample point.
![]()
Question 3.
Describe the sample space for the indicated experiment, (i) A coin is tossed three times.
Answer:
Sample space = S
= {HHH, HHT, HTH, THH, TTT, TTH, THT, HTT}
(ii) A die is thrown two times.
Answer:
Required sample space = S
= {(x,y) : x,y ∈ {1,2,3,4,5,6}}
= {(x,y) : x,y = 1,2,3,4,5,6}
= {(1.1). (1,2)(1,3), (1,4), (1,5), (1,6),
= (2,6), ……………… , (3,1), …………….. , (3,6), (4,1), ……………. , (4,6),
(5,6), …………. (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}
(iii) A coin is tossed four times.
Answer:
S = {HHHH, HHHT, HHTH, HTHH,THHH, HHTT, HTHT, HTTH, THHT, THTH,
TTHH, HTTT, THTT,TTHT, TTTH ,TTTT}
(iv) A coin is tossed and then a die is rolled only in case a head is shown on the coin.
Answer:
Required sample space = S = {H1,H2,H3,H4,H5,H6,T}
(v) A coin is tossed and a die is thrown.
Answer:
Required sample space = S
= {(x, y): x ∈ {H, T}, y ∈ {1,2,3,4,5,6}}
= {(H, 1), (H ,2),(H ,3), (H ,4) (H ,5), (H ,6),
(T, 1)(T, 2)(T, 3), (T, 4), (T, 5), (T, 6)}
= {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}
Question 4.
2 boys and 2 girls are in room X and 1 boy and 3 girls are in room Y. Specify the sample space for the experiment in which a room is selected and then a person.
Answer:
Let boys be denoted by BX, B2, B3 and girls be G1, G2, G3, GA, G5
Then the required sample space = S.
= {XB1, XB2, XG, XG2, YB, YG, YGA, YGS}
Here B1, B1, G1, G2 are associated with X and B3, Gb, Ga, Gs are associated with Y.
![]()
Question 5.
One die of red colour, one of white colour and one of blue colour are placed in a bag. One die is selected at random and rolled, its colour and the number on its uppermost face is noted. Describe the sample space.
Answer:
Let R,W,B be the red die, white die, blue die respectively.
∴ Required sample space = S
= {R1, R2, R3, R4, R5, R6,
W1, W2, W3, W4, W5, W6,
B1, B2, B3, B4, B5, B6}
Question 6.
An experiment consists of recording boy – girl composition of family with 2 children,
(i) What is the sample space if we are interested in knowing whether it is a boy or girl in the order of their births?
(ii) What is the sample space if we are interested in the number of girls in the family?
Answer:
Let B stands for boys and G stands for girl. Then
(i) Required sample space = S
= {BB, BG, GB, GG}
Required sample space = {0, 1, 2}
Question 7.
A box contains 1 red and 3 identical white balls. Two balls are drawn at random in succession without replacement. Write the sample space for this experiment.
Answer:
Let R stands for red ball and W stands for white ball. Then required sample space = S
= {RW, WR, WW}
= {R,W),(W,R),(W,W)}
Question 8.
An experiment consists of tossing a coin and then throwing it second time if a head occurs. If tail occurs on the first toss, then a die is rolled once. Find the sample space.
Answer:
Sample space = S
= {HH, HT, T1, T2,T3, T4, T5, T6}
![]()
Question 9.
Suppose 3 bulbs are selected at random from a lot. Each bulb is tested and classified as defective (D) or non-defective (N). Write the sample space of this experiment.
Answer:
Required sample space = S
= {DDD, DDN, DND, NDD, NNN, NND,NDN,DNN}
Question 10.
A coin is tossed. If the outcome is a head, a die is thrown. If the die shows up an even number, the die is thrown again. What is the sample space for the experiment?
Answer:
Required sample space = S
= {T, H1, H3, H5, H21, H22, H23, H24, H25, H26,
H41, H42, H43, H44, H45, H46,
H61, H62, H63, H64, H65, H66}
Question 11.
The numbers 1, 2, 3 and 4 are written separately on four slips of paper. The slips are put in the box and mixed thoroughly. A person draws two slips from the box one after the other without replacement. Write the sample space for the experiment.
Answer:
Required sample space – S
= {(1,2), (1,3), (1,4), (2,1), (2,3),
(2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3)}
Question 12.
An experiment consists of rolling a die and then tossing a coin once if the number on the die is even. If the number on the die is odd, the coin is tossed twice. Write the sample space for this experiment.
Answer:
Required sample space = 5
= {2H, 2T, 4H, 6H, 6T, 1HH
1HT, 1TH, 1TT, 3HH, 3HT,
3TH, 3TT, 5HH, 5HT 5TH, 5TT}
![]()
Question 13.
A coin is tossed. If it shows tail, we draw a ball from a box which contains 2 red and 3 black balls. If it shows head, we throw a die. Find the sample space for this experiment?
Answer:
Required sample space = S = {TR1, TR2, TB1, TB2, TB3, H1, H2, H3, H4, H5, H6}
Here R1,R2 are two red balls and B1,B2,B3 are three black balls.
Question 14.
Define the following terms,
(i) Event
(ii) Impossible event
(iii) Sure event
(iv) Simple event (Elementary event)
(v) Compound event.
Answer:
(i) Event: Any subset E of a sample space S is called an event.
(ii) Impossible even: The empty set φ describes an events. Then φ is called an impossible event.
(iii) Sure event: The sample space S describes an event. Then S, sample space is called the sure event.
(iv) Simple event: If an event E has only one sample point of a sample space, it is called a simple event.
(v) Compound event: If an event has more than one sample point, it is called a compound event.
![]()
Question 15.
Define: Complementary event, the event ‘A or B’, the event ‘A and B’, the event ‘A but not B’, mutually exclusive events, exhaustive events and mutually exclusive and exhaustive events.
Answer:
(i) Complementary event (‘not event’): Let A be event associated with an experiment whose sample space is S. Then, the complementary event ‘not A’ to the event A is denoted by A’ and is defined as A’ = { ω : ω ∈ S and ω ∉ A} = S-A
(ii) The even ‘A or B’: The sets A and B are two events associated with a sample space, then ’A ∪ B’ is the event ‘either A or B or both’, this event is called‘A or B’.
i.e., ’A or B’ = A ∪ B = {ω : (ω ∈ A or ω ∈ B]
(iii) The event ‘A and B’: If A and B are two events, then the set A ∩ B denotes the event ‘A and B’.
∴ ’A and B’= A ∩ B = {ω : ω ∈ A and ω ∈ B}
(iv) The event ‘A but not B’: If A and B are two events associated with an experiment, then the set A – B denotes the event ‘A but not B’.
Note: A-B = A ∩ B’
(v) Mutually exclusive events: If A and B are two events associated with an experiment, then A and B are called mutually exclusive events if they cannot occur simultaneously. In this case A ∩ B = ϕ
Note: A and B are disjoint sets.

Question 16.
Consider the experiment of rolling a die. Let A be the event ‘getting a prime number, B be the event ‘getting an odd number’. Write the sets representing the events”
(i) ‘A or B’
(ii) ‘A and B’
(iii) ‘not A’
(iv) ‘A but not B’.
Answer:
We have, the sample space of an experiment of rolling a die is S = {1,2,3,4,5,6}
Here, A = {2,3,5} and B = {1,3,5}
(i) ’A or B’=A ∪ B = {1,2,3,5}
(ii) ’A and B’=A ∩ B = {3,5}
(iii) ’not A’= A’ = S – A = {1,4,6}
(iv) ’A but not B ’= A – B = {2}
![]()
Question 17.
Two dice are thrown and the sum of the numbers which comes up on the dice is noted. Let us consider the following events associated with this experiment.
A : ‘the sum is even’
B : ‘the sum is a multiple of 3’
C: ‘the sum is less than 4’
D: ‘the sum is greater than 11’.
Which pairs of these events are mutually exclusive?
Answer:
We have, sample space
= S = {(x,y) : x,y =1, 2, 3, 4, 5, 6}
i.e., 5 = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1),………… (2,6), (3,1), ……….. ,(3,6),
(4,6),……….. (5,1), …………… (5,6),
(6,1),(6,2),(6,3),(6,4), (6,5),(6,6)}
Now, A = {(1,1), (1,3), (1,5), (2,2), (2,4), (2,6)
(3,3), (3,5), (4,2), (4,4), (4,6), (5,1), (5,3), (5,5), (6,4), (6,6)}
B = {(1,2), (1,5), (2,4), (3,3), (3,6), (4,5),
(2,1),(4,2),(5,4),(6,3),(6,6)}
C = {(1,1),(1,2),(2,1)}
D = {(6,6)}
We find that,
A ∩ E = {(1,5), (2,4), (3,3), (4,2), (5,1), (6,6)}
⇒ A ∩ B ≠ ϕ
⇒ A and B are not mutually exclusive events.
Similarly,
A ∩ C ≠ ϕ, A ∩ D ≠ ϕ
B ∩ C≠ ϕ,B ∩ D ≠ ϕ, C ∩ D≠ ϕ
Thus the pairs (A, C), (A, D), (B, C) and (B, D) are not mutually exclusive events and pair (C, D) are mutually exclusive events.
Question 18.
A coin is tossed three times, consider the following events,
A : ‘no head appears’.
B: ‘exactly one head appears’
C: ‘at least two heads appear’
Do they form a set of mutually exclusive and exhaustive events?
Answer:
The sample space of the experiment is,
S ={HHH, HHT, HTH, THH, ITT, TTH, THT, HTT}
Here, A = {m},B = {TTH, THT, HTT}
C = {HHT, HTH, THH, HHH}
Now, A ∪ B ∪ C = {TTT, TTH, THT, HTT, HHT, HTH, THH, HHH}
⇒ A ∪ B ∪ C = S
⇒ A, B and C are exhaustive events.
Also A∩B = ϕ,A∩C = ϕ and B∩C = ϕ
⇒ A, B and C are mutually exclusive.
Hence A, B and C are mutually exclusive and exhaustive events.
![]()
Question 19.
A die is rolled. Let E be the event “die shows 4” and F be the event “die shows even number”. Are E and F mutually exclusive?
Answer:
The sample space of an experiment is,
5 = {1,2,3,4,5,6}
Here, E = {4} and F = {2,4,6}
Now, E ∩F = {4} ≠ ϕ
⇒ E and F are not mutually exclusive.
Question 20.
A die is thrown. Describe the following events;
(i) A: a number less than 7.
(ii) B: a number greater than 7
(iii) C: a multiple of 3.
(iv) D: a number less than 4.
(v) E : an even number greater than 4.
(vi) F: a number not less than 3. Also find A ∪ B, A ∩ B, B ∪ C, E ∩ F, D ∩ E, A – C, D – E,
E ∩ F’
Answer:

Question 21.
An experiment involves rolling a pair of dice and recording the numbers that come up. Describe the following events: A: the sum is greater than 8, B: 2 occurs on either die. C: the sum is atleast 7 and a multiple of 3. Which pairs of these events are mutually exclusive?
Answer:
We have, sample space
S ={(x,y) : x,y = 1,2,3,4,5,6}
Then, A = {(3,6), (4,5), (4,6), (5,4), (5,5),
(5,6), (6,3), (6,4), (6,5), (6,6)}
B = {(1,2), (2,2), (3,2), (4,2), (5,2),
(6,2) , (2,1), (2,3), (2,4), (2,5), (2,6)}
C = {(3,6), (4,5), (5,4), (6,3), (6,6)}
Now A ∩ B = { } = ϕ
A ∩ C = {(3,6), (4,5), (5,4), (6,3), (6,6)}
B ∩ C = { } = ϕ
∴ A and B, B and C are mutually exclusive events.
![]()
Question 22.
Three coins are tossed once. Let A denote the event ‘three heads show’, B denote the event ‘two heads and one tail show’, C denote the event ‘three tails show’ and D denote the event ‘a head shows on the first can’. Which events are
(i) mutually exclusive?
(ii) simple ?
(iii) compound?
Answer:
We have, sample space
= S = {HHH, HHT, HTH, THH, TTT, TTH, THT, HTT)
Then
A = {HHH}
B = {HHT, HTH, THH}
C = {T,T,T}
D = {HHH, HTH, HHT, HTT}
(i) Clearly A ∩ B = ϕ, A ∩ C = ϕ, C ∩ D = ϕ
⇒ A and B ,A and C ; C and D are mutually exclusive.
(ii) A, C are simple events.
(iii) B, D are compounds events.
Question 23.
Three coins are tossed. Describe (i) Two events which are mutually exclusive, (ii) Three events which are mutually exclusive and exhaustive, (iii) Two events, which are not ‘ mutually exclusive (iv) Two events which are mutually exclusive but not exhaustive, (v) Three events which are mutually exclusive but not exhaustive.
Answer:
Let (i)
A: ‘atleast two heads appear’
B: ‘atleast two tails appear’
Here, A = {HHT, HTH, THH, HHH}
B = {TTH, THT, HTT, TTT}
∴ A ∩ B = ϕ , ⇒ A, B mutually exclusive.
(Note: Give any suitable example (events) associated with experiment)
(ii) Let A : ‘No tail appears’
B: ‘Exactly one tail appears’
C: ‘Atleast two tails appear’
Here A = {HHH]
B = {THH, HTH, HHT}
C = {TTH, THT, HTT, TTT}
Clearly, A ∪ B ∪ C = sample space = S and A ∩ B = ϕ , B ∩ C = ϕ, A ∩ C
∴ A, B, C are mutually exclusive and mutually exclusive and exhaustive events.
![]()
(iii) Let
A: ‘almost two tails appear’
B: ‘exactly two tails appear’
Here,
A = {HHH, THH, HTH, HHT, HTT, THT, TTH}
B = {HTT,THT,TTH}
Clearly, A ∩ B ≠ ϕ
∴ A and B are not mutually exclusive
(iv) ‘Getting exactly one head’ and ‘Getting exactly two heads’. (Try the explanation)
(v) ‘Getting exactly one tail’, ‘Getting exactly two tails’ and ‘Getting exactly three tails’. (Try explanation)
Question 24.
Two dice are thrown. The events A, B, and C are as follows. A: getting an even number on the first die. B: getting an odd number on the first die. C: getting the sum of the numbers on the dice < 5. Describe the events: (i) A’ (ii) not B (iii) A or B (iv) A and B (v) A but not C (vi) B or C (vii) B and C (viii) A∩B’∩C’.
Answer:
We have, sample space S of the experiment is 5={(x,y):x,y = l,2,3,4,5,6}
Then A = {(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(4.1), (4,2), (4,3), (4,4), (4,5), (4,6)
(6.1),(6,2),(6,3),(6,4),(6,5),(6,6)}
B = {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(3.1) , (3,2), (3,3), (3,4), (3,5), (3,6),
(5.1) , (5,2), (5,3), (5,4), (5,5), (5,6)}
C = {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3)
(3.1) , (3,2), (4,1)}
(i) A’ = B (ii) B’ = A (iii) A∪B = S (iv) A∩B = ϕ (v) A – C = {(2,4),(2,5),(2,6),(4,2),(4,3) , (4,4), (4,5), (4,6), (6,1), (6,2), (6,3), (6,4),(6,5),(6,6)}
(vi) B ∪ C = {(1,1), (1,2), ………… (1,6), (2,1), (2,2),
(2.3),(3,1), (3,2), (3,3), ……….. (3,6), (4,1), (5,1), (5,2),(5,6)}
(vii) B ∩ C = {(1,1),(1,2),(1,3),(1,4),(3,1),(3,2)}
![]()
(viii) Here, C’ = S – C and B’ = A
∴ A ∩ B’∩ C’ = A ∩ A ∩ C’
= A ∩ C’
= {(2,4), (2,5), (2,6), (4,2),
(4.3), (4,4), …………, (4,6), (6,1), (6,2), ………. , (6,6)}
Axiomatic Approach to Probability
Let S be the sample space of a random experiment. The probability P is a real valued function whose domain is the power set of S and range is the interval [0, 1]. Satisfy the following axioms.
- For any event E, P(E) ≥ 0
- P(S) = 1
- If E and F are mutually exclusive then P(E∪F) = P(E) + P(F).
Note:
(1) P (sure event) = 1
(2) P (impossible event) = 0
(3) P(ϕ) = 0
(4) Let S = sample space of a random experiment containing outcomes
ω1, ω2 , ω3, ……….. ωn then
(i) 0 ≤ P(ω1) ≤ 1 for each ω1 ∈ S
(ii) P(ω1) + P(ω2) +. ……… + P(ω3) = 1
(iii) For any event A, P(A) = ΣP(ωi) where ωi, ∈ ωi
Note: P(ωi) = P({ωi})
Question 1.
Define equally likely outcomes.
Answer:
All the outcomes with equal probability are called equally likely outcomes.
Note: Let S = {ω1, ω2, ………….. ωn} and all the outcomes are equally likely outcomes, i.e.,
P(ω1) = p, for all ωi, ∈ S, 0≤ p ≤ 1
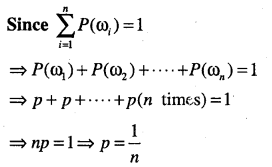
Question 2.
Define the probability of an event. A’: ‘card drawn is not a diamond’
Answer:
For a finite sample space S with equally likely We have n(A) = 13, n(S) = 52
outcomes, probability of an event A is denoted by \(P(A)=\frac{n(A)}{n(S)}\), Where n(A) = number of elements in the set A n(S) = number of elements in the set S.
Note:
(i) If A and B are any two events, then
P(A or B) = P(A) + P(B) – P(A and B)
i.e., P( A ∪ B) P(A) + P(B) – P(A ∩ B)
(ii) If A and B around mutually exclusive, then
P (‘A or B’) = P(A) + P(B)
i.e., P(A ∪ B) = P(A) + P(P) ∵ A ∩B = ϕ
(iii) If A is any event, then
P(‘not A’ ) = P(A’) = 1 – P(A)
![]()
Question 3.
One card is drawn from a well shuffled deck of 52 cards. If each outcome is equally likely, calculate the probability that the card will be (i) a diamond (ii) not an ace (iii) a black card (i.e., a club or a spade) (iv) not a diamond (v) not a black card.
Answer:
When a card is drawn from a well shuffled deck of 52 cards, the number of possible outcomes is 52.
(i) Let A : ‘the card drawn is a diamond’ Clearly the number of elements in set A is 13.
∵ n(S) = 52 and n(A) = 13
∴ P(A)=\(\frac{n(A)}{n(S)}=\frac{13}{52}=\frac{1}{4}\)
(ii) Let B: ‘card drawn is an ace’.
B’: ‘card drawn is not an ace’
we have, n(13) = 4,n(S)= 52
P(B)=\(\frac{n(B)}{n(S)}=\frac{4}{52}=\frac{1}{13}\)
Required probability =P(B’)
\(\text { We have, } \left(B^{\prime}\right)=1-P(B)=1-\frac{1}{13}=\frac{12}{13}\)
(iii) Let C : ‘card drawn is black card’.
∴ Number of elements in set C = 26
i.e., n(C) =26
P(C)=\(\frac{n(C)}{n(S)}=\frac{26}{52}=\frac{1}{2}\)
(iv) Let A: ‘card drawn is a diamond’
∴ A’: card drawn is not a diamond’
We have n(A) = 13, n(S) = 52
p(A)=\(\frac{13}{52}=\frac{1}{4}\)
\(\text { We have, } P\left(A^{\prime}\right)=1-P(A)=1-\frac{1}{4}=\frac{3}{4}\)
(v) We have p(C) = \(\frac{1}{2}\) (from (iii))
p\(\left(C^{\prime}\right)=1-P(C)=1-\frac{1}{2}=\frac{1}{2}\)
Question 4.
A coin is tossed twice, what is the probability that atleast one tail occurs?
Answer:
Required sample space = S
= {HH,HT,TH,TT}.
Let A: ‘atleast one tail occurs’A = {HT,TH,TT}
We have, n(A) = 3, n(S) = 4 = 22
Required probability \(=P(A)=\frac{n(A)}{n(S)}\)
\(=\frac{3}{4}\)
![]()
Question 5.
A die is thrown, find the probability of following events: (i) A prime number will appear, (ii) A number greater than or equal to 3 will appear, (iii) A number less than or equal to one will appear, (iv) A number more than 6 will appear, (v) A number less than 6 will appear.
Answer:
Required sample space associated with an experiment is S = {1, 2, 3,4, 5, 6}
∴ n(S) = 6
(i) Let A : ‘a prime number will appear’
⇒ A = {2,3,5} ∴ n(A) = 3
∴ Required Probability
\(P(A)=\frac{n(A)}{n(S)}=\frac{3}{6}=\frac{1}{2}\)
(ii) Let B: ‘a number ≥ 3 will appear’
⇒ B = {3,4,5,6} ∴ n(B) = 4
∴ Required Probability
\(P(B)=\frac{n(B)}{n(S)}=\frac{4}{6}=\frac{2}{3}\)
(iii) Let C: ‘a number ≤ 1 will appear’
⇒ C = (1)
∴ Required Probability
\(P(C)=\frac{n(C)}{n(S)}=\frac{1}{6}\)
(iv) Let D: ‘a number >6 will apper’
⇒ D = { } = ϕ \(=P(D)=\frac{0}{6}=0\)
(v) E : ‘ a number < 6 will appear’
⇒ E= {1, 2, 3, 4, 5} ∴ n(E) = 5
∴ Required probability
\(=P(E)=\frac{n(E)}{n(S)}=\frac{5}{6}\)
Question 6.
A card is selected from a pack of 52 cards,How many points are there in the sample space? (b) Calculate the probability that the card is an ace of spades, (c) Calculate the probability that the card is (i) an ace (ii) black card.
Answer:
We have, number of possible outcomes = 52
n(S) = 52= 52C1
(a) There are 52 points in the sample – space.
(b) Let A: ‘a selected card is an ace of spades’ Clearly the number of elements in the set A is 1. i.e., n(A) =1C1
∴ Required probability
\(=P(A)=\frac{n(A)}{n(S)}=\frac{1}{52}\)
(c) (i) Let B: ‘a selected card is an ace’ we know that, in a deck of 52 cards, there are 4 different aces.
∴ n(B) = 4= 4C1
∴ Required probability
\(=P(B)=\frac{n(B)}{n(S)}=\frac{4}{52}=\frac{1}{13}\)
(ii) Let C: ‘a selected card is black’ There are 26 black cards in a pack o f 52 cards
∴ n(C) = 26C1 = 26
∴ Required probability
\(=P(C)=\frac{n(C)}{n(S)}=\frac{26}{52}=\frac{1}{2}\)
![]()
Question 7.
A fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. Find the probability that the sum of numbers that turn up is (i) 3 (ii) 12.
Answer:
We have, a sample space associated with an experiment is
S = {(x, y): x = 1,6 and
y = 1.2,3,4,5,6}
= {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (6,2), (6,3), (6,4), (6,5), (6,6)}
∴ n(S) = 12
(i) Let A: ‘sum of the numbers that turn up is 3’
∴ A = {(1,2)} ∵ 1 + 2 = 3
⇒ n(A) = 1
∴ Required probability
= \(P(A)=\frac{n(A)}{n(S)}=\frac{1}{12}\)
(ii) Let B: ‘sum of the numbers that turn up is 12’.
⇒ B = {(6,6)} ∵ 6 + 6 = 12
∴ Required probability
=\(P(B)=\frac{1}{12}=\frac{n(B)}{n(S)}\)
Question 8.
There are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman?
Answer:
Number of members on the city council
= 4 + 6=10
n(S)= 10C1 =10
Let A: ‘selected member is a woman’
⇒n(A)= 6C1=6
∴ Required probability
=\(P(A)=\frac{n(A)}{n(S)}=\frac{6}{10}=\frac{3}{5}\)
Question 9.
A fair coin is tossed four times, and a person win Rs. 1 for each head and lose Rs. 1.50 for each tail that turn up. From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts.
Answer:
We have,
Required sample space = 5
= {HHHH, HHHT, HHTH, HTHH,
THHH, HHTT, HTHTJHTH,
TTHH,HTTH,THHT, TTTH ,TTHT ,THTT ,HTTT, TTTT}
∴ n(S) = 16 = 24

Question 10.
Three coins are tossed once. Find the probability of getting (i) 3 heads (ii) 2 heads (iii) at least 2 heads (iv) atmost 2 heads (v) no head (vi) 3 tails (viii) exactly 2 tails (viii) no tail (ix) atmost two tails.
Answer:
We have,
Required sample space associated with an experiment is
S={HHH,HHT,HTH,THH,TTH, THT,HTT,TTT }
n(5) = 23 =8
(i) Let A: ‘getting 3 heads’
∴ A = {HHH}=n(A) = 1
P(A)=\(\frac{n(A)}{n(S)}=\frac{1}{8}\)
(ii) Let B: ‘getting 2 heads’
∴ B = {HHT,HTH,THH}
⇒ n(B) = 3


Note:
(i) atleast means >
(ii) atmost means <
(iii) exactly means =
(iv) at least one of E1 and E2 = E1 or E2
![]()
Question 11.
If \(\frac{2}{11}\) is the probability of an event A, what is the probability of the event ‘not A’.
Answer:
Given that P(A) =\(\frac{2}{11}\)if A is an event.
To find: P (‘not A’) = P(A’)
Since P(A’) = 1 – P(A)
\(=1-\frac{2}{11}=\frac{9}{11}\)
Question 12.
A letter is chosen at random from the word ‘ASSASSINATION’. Find the probability that letter is (i) a vowel (ii) a consonant.
Answer:
In the word ASSASSINATION, we have A – 3 ;
S – 4; I – 2; N – 2, O – 1 and T- 1.
Total number of letters = 13.
Among them, the vowels are: A – 3, I – 2, 0 – 1 is vowels are 6 in number.
The consonants are: S – 4 ; N – 2, T-1.
i.e., co-consonants are 7 in number.
(i) P (a vowel) = \(\frac{6}{13}\)
(ii) P (a consonant) = \(\frac{7}{13}\)
Question 13.
In a lottery, a person choose, six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game? (order of the numbers is not important).
Answer:
A person can choose 6 natural number out of 20 in 20C6 ways.
n(S)=MC6
Let A : ‘he wins the prize’
∴ n(A) = 6C6 = 1
∵ There is only one chance which will match the six numbers already fixed by the committee.


Question 14.
Check whether the following probabilities P(A) and P(B) are consistently defined,
(i) P(A) = 0.5, P(B) = 0.7, P(A∩B) = 0.6
(ii) P(A) = 0.5, P(B) = 0.4, P(A ∪ P) = 0.8
Note: P(A) and P(B) P(A ∩ B) are consistently defined iff P(A∩B) ≤ P(A) and P(B)
Answer:
(i) P(A) = 0.6 and P(B) = 0.7 and P(A ∩ B) = 0.6
Here, p(A n B) > P(A) and P(A ∩ B)< P(B)
P(A ∩ B) is not less than or equal to P(A) and P(B)
∴ P(A) and P(B), P(A n B) are not consistently defined.
(ii) We have, P(A ∪ B) = P(A) + P(B) – p(A ∩ B)
P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= 0.5 + 0.5 – 0.8
= 0.9 – 0.8 = 0.1
∴ P(A ∩ S) = 01
Here, P(A ∩ B) is less than P(A) and P(B)
P(A) and P(B)P(A ∪ B) are consistently defined.
(Note: P(A ∪ B)<P(A) + P(B))
![]()
Question 15.
(i) If P(A) = \(\frac{1}{3}\) ,P(B) = \(\frac{1}{5}\),
P(A ∩ B) = \(\frac{1}{15}\) , find P(A ∪ B)
(ii) If P(A) = 0.35, P(A ∩ B) = 0-25,P(A ∪ B) = 0’6, find P(B)- (iii) If P(A) = 0-5,
P(B) = 0-35, P< A ∪ B) = 0.7, find P(A ∩ B)’
Answer:
(i) We have,
P( A ∪ B) = P(A) + P(B) – P(A ∩ B)
\(=\frac{1}{3}+\frac{1}{5}-\frac{1}{15}=\frac{5+3-1}{15}=\frac{7}{15}\)
(ii) P(B) = 0.5 (Try yourself)
(ii) P(A∩B) = 015 (Try)
Question 16.
Given \(P(A)=\frac{3}{5} \quad \text { and } \quad P(B)=\frac{1}{5}\).
find p(‘A or B’), if A and B are mutually exclusive events.
Answer:
Since A and B are mutually exclusive then

Question 17.
If E and F are events such that \(P(E)=\frac{1}{4}, P(F)=\frac{1}{2} \text { and } P(E \text { and } F)=\frac{1}{8}\). Find(i) P(E or F) (ii) P (not E and not F)
Answer:

Question 18.
Events E and F are such that P (not E or not F) = 0.25, State whether E and F are mutually exclusive.
Answer:
Given: P (not E or not F) = 0.25
i.e., P(E’orF’) = 0.25
i.e., P(E’∪F’) = 0.25
i.e., P((E∩F)’) = 0.25
i.e., 1-P(E∩F) = 0.25
i.e., P(E∩F) = 1- 0.25 = 0-75 ≠ 0
∴ E and F are not mutually exclusive.
( ∵ condition, for mutually exclusive events is P(E∩F) = 0)
Question 19.
A and B are events such that P(A) = 0.42, P(B) = 0.48 and P(A and B) = 016 .Determine (i) P(not A) (ii) P(not B) (iii) P(A or B)
Answer:
(i) P(not A) = P(A’) = 1 – P(A) = 0. 58
(ii) P(not B} = P(B’) = 1 – P(B) = 0-52
(iii) P(A or B) = P(A∪B) = 014 (Try)
![]()
Question 20.
In class XI of a school 40% of the students study mathematics, and 30% study biology. 10% of the students study both mathematics and biology. If a student is selected at random from the class, find the probability that he will be studying mathematics or biology.
Answer:
Let M : ‘student study maths’

Question 21.
In an entrance test that is graded on the basis of two examinations, the probability of randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0.7. The probability of passing atleast one of them is 0.95. What is the probability of passing both?
Answer:
Let A: student passes first examination B: student passes second examination
Given: P(A) = 0.8, P(B) = 0 .7 and
P(A∪B) = 0.95
To find: P(A∩B)
∵ P(A∩B) = P(A) + P(B) – P(A∪B)
= 0.55 (Try)
Question 22.
The probability that a student will pass the final examination in both English and Hindi is 0.5 and the probability of passing neither is 0.1. If the probability of passing the English Examination is 0.75, what is the probability of passing the Hindi examination?
Answer:
Let A: student passes in English.
B: Student passes in Hindi
Given: P(A) = 0.75, P(A∩B) = 0.5 and P (neither A nor B) = P((A ∪ B)’) = 01
To find: P(B)
Now, P((A∪B)’) = 1- P(A∪B)
⇒ 0.1=1 – P(A∪B) ∵ P((A∪B)’) = 01
∴ P{A ∪ B) = 1- 01 = 0.9
P(A) + P(B) – P(A ∩ B) = 0. 9
∴ 0.75 + P(B) – 0.5 = 0.9
∴ P(B) = 1.4 – 0.75 = 0.65
Question 23.
In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that, (i) The student opted for NCC or NSS (ii) The student has opted neither NCC nor NSS (iii) The student has opted NSS but not NCC.
Answer:
Let A: student opted for NCC
B : student opted for NSS

![]()
Question 24.
A bag contains 9 discs of which 4 are red, 3 are blue and 2 are yellow. The discs are similar in shape and size. A disc is drawn at random from the bag. Calculate probability that it will be (i) red, (ii) yellow, (iii) blue, (iv) not blue, (v) either red or blue.
Answer:
We have, number of discs = 9 = 4 + 3 + 2.
Possible outcomes are 9. n(S) = 9
Let A: ‘Drawn disc is red.’
B: Drawn disc is blue.
C: Drawn disc is yellow.

Question 25.
Two students Anil and Ashima appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10. The probability that both will qualify the examination is 0.02. Find the probability that Both (a) Anil and Ashima will not qualify the examination,
(b) Atlast one of them will not qualify the examination,
(c) Only one of them will qualify the examination.
Answer:
Let A: Anil qualify the examination B: Ashima qualify the examination
Given: P(A) = 0.05, P(B) = 010 and P(A∩B) = 0. 02
(a) A’ : Anil will not qualify the exam and B’ : Asima will not qualify the exam.
To find: P(A’∩B’) = P((A∪B)’) = 1 -P(A∩B)
We have, P(A∪B) = P(A) +P(B)~ P(A∩B)
= 0 05 + 0.10-0 02
P(A∪B) = 013
P(A’ ∩ B’) = 1 – P(A ∪ B) = 1 – 013 = 0.87
(b) We have
P (atleast one of them will not qualify the examination)
= 1 – P (both of them will qualify)
= 1 – P(A∩B)
= 1- 0.02 =0.98
(c) Only one of them will qualify
= (Anil will qualify and Ashima will not)
or
(Anil will not qualify and Ashima will)
= (A∩B’) or (A’∩B)
= (A∩B’)∪(A’∩B)
Required probability
= P((A∩B’)∪(A’∩B)
= P(A∩B’) + P(A’∩B)
= P(A)-P(A∩B) + P(B) – P(A∩B)
= 0-05+ 010 – 2(0.02)
= 0 15 – 0 04 = 0.11
Question 26.
A committee of two persons is selected from two men and two women. What is the probability that the committee will have (a) no men? (b) one man? (c) two men?
Answer:
Total number of persons = 2 + 2 = 4.
Out of the 4 persons, two can be selected in 4C2 ways. n(S) = 4C2
(a) No men in the committee of two
⇒ two women in the committee of two.
⇒ two women can be selected in 2C2 ways.

Question 27.
Find the probability that when a hand of 7 cards is drawn from a well shuffled deck of 52 cards, it contains (i) all kings, (ii) 3 kings, (iii) at least 3 kings.
Answer:
Total number of possible hands = 52C7
(i) Number of hands with 4 kings (all kings)

![]()
Question 28.
It A, B, C are three events associated with a random experiment, prove that
P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) -P(A∩C)-P(B∩C) + P(A∩B∩C)
Answer:
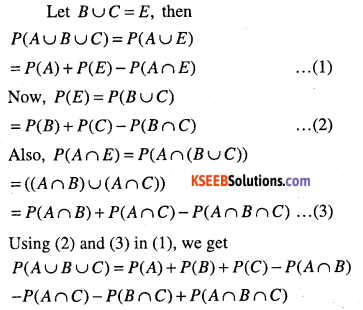
Miscellaneous examples
Question 29.
A box contains 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from a box, what is probability that (i) all will be blue (ii) atleast one will be green.
Answer:
Total marbles \(=10+20+30=60\)
∴ 5 marbles can be drawn out of 60 in 60C5 ways.
(i) 5 blue marbles out of 20 can be drawn in 20C5 ways.

Question 30.
4 cards are drawn from a well-shuffled deck of 52 cards. What is the probability of obtaining 3 diamonds and one spade?
Answer:
4 cards can be drawn from 52 in 52C4 ways.
P (3 diamond and one spade)
\(=\frac{C_{3} \times^{13} C_{1}}{^{52} C_{4}}=\frac{286}{20825}(\text { Try })
\)
∵ 13 diamond cards and 13 spade cards in a pack of [1] cards.
Question 31.
A die has two faces each with number ‘1’, three faces each with number ‘2’ and one face with number ‘3’. If die is rolled once, determine, (i) P (2) (ii) P (1 or 3) (iii) P (not 3)
Answer:
We know that, die has 6 faces.

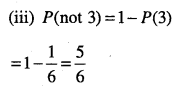
Question 32.
In a certain lottery 10,000 tickets are sold and ten equal prizes are awarded. What is the probability of not getting a prize if you buy (a) one ticket (b) two tickets (c) 10
Answer:
(a) One ticket out of 10,000 tickets can be selected in 10000C1 ways.
One ticket with prize can be selected in out of 10 in 10C1 ways.

![]()
Question 33.
Three letters are dictated to three persons and an envelope is addressed to each of them, the letters are inserted into the enveloped at random so that each envelope contains exactly one letter. Find the probability that atleast one letter is in its proper envelope.
Answer:
Total number of ways of putting three letters into three envelopes is
3 P3 = 3! (ways) = 6.
The number of ways in which none of the letter is put into proper envelope is 2.
\( (\text { none })=\frac{2}{6}=\frac{1}{3}\)
∴ p(atleast one letter is in its proper envelop)
= 1-p (none)
= \(1-\frac{1}{3}=\frac{2}{3}\)
Question 34.
A and B are two events such that P (A) = 0.54, P (B) = 0.69, P(A∩B) = 0.35. Find
(i) P(A∪B) (ii) P(A’∩B’) (iii) P(A∩B’) (iv) P(B∩A’)
Answer:
Try your self
(i) 0.88 (ii) 0.12 (iii) 0.19 (iv) 0.34.
Question 35.
If 4 – digit numbers greater than 5,000 are randomly formed from the digits 0,1, 3, 5 and 7. What is the probability of forming a number divisible by 5 when, (i) digits are repeated (ii) digits are not repeated.
Answer:
Required 4-digit number is greater than 5000.
(i) digits are repeated.
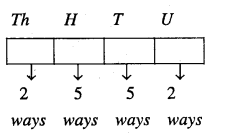
∴ Number of numbers greater than 5000 is 2 x 5 x 5 x 5 = 250.
If the number is divisible by 5 then unit place can be filled with either 0 or 5.
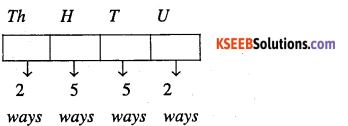
∴ Required probability
\(=\frac{100}{250}=\frac{2}{5}\)
(ii) Required of the digits is not allowed
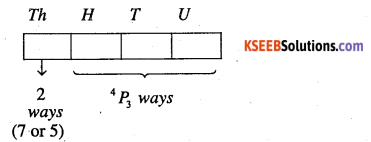
∴ Number of numbers > 5000 that can be formed = 2 x 4P3 = 48.
The numbers which are divisible by. 5 have either 0 or 5 in the unit places.
Case I:
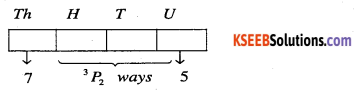
∴ Number of numbers divisible by 5 of this type = 1 x 3P2 =3 x 2 = 6
(Here 7 is fixed for thousand place and 5 is found for unit place)
Case II:
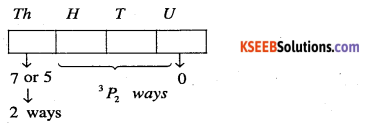
Here O is fixed for unit place and thousand place can be filled in two ways
(either by 7 or 5).
Remaining places can be filled in with remaining 3 digits by 3P2 = 6 ways.
∴ Number of numbers divisible by 5 of this type (kind) = 2 x 3P2 = 2 x 6 = 12.
∴ Number of numbers divisible by 5 = 6+12 = 18
∴ Required probability \(=\frac{18}{48}=\frac{3}{8}\)
![]()
Question 36.
The number look of a suitcase has 4 wheels, each labeled with ten digits i.e. from 0 to 9. The lock will opens with a sequence of four digits with no repeats. What is the probability of a person getting the right sequence to open the suitcase?
Answer:
Number of all possible sequences

∴ Number of sequences of 4 distinct digits = 10 x 9 x 8 x 7 = 5040
∴ Required probability
\(=\frac{1}{5040}\)
(Numerator = 1, because the suitcase open for only one right sequence.)