1st PUC Maths Question Bank Chapter 8 Binomial Theorem

Students can Download Maths Chapter 8 Binomial Theorem Questions and Answers, Notes Pdf, 1st PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 1st PUC Maths Question Bank Chapter 8 Binomial Theorem

Question 1.
State and prove Binomial theorem.
Answer:

Some observations in a binomial theorem:
(1) The expansion of {a + b)ⁿ has (n + 1) terms
(2) The coefficients ⁿC_r occurring in the binomial theorem are known as binomial coefficients.
(3) The indices of V go on decreasing and that of ‘a’ go on increasing by 1 at each stage.
i.e., for each term: index of a + index of b-n.
(4) Since ⁿC_r=ⁿC_n__r we have
ⁿC₀ =ⁿC_n, ⁿC_x =ⁿC_n__r and so on.
Thus the coefficients of the terms equidistant from the beginning and the end in a binomial theorem are equal.
(5) General term in (a + b)ⁿ: T_r+1 – ⁿC_r a^n–rb^r
(6) Middle terms in (a + b)ⁿ

• When ‘n’ is even, the middle term
  \(=\left(\frac{n}{2}+1\right)^{t h} \text { term }\)
• When ‘n’ is odd ,the middle term are
  \(\frac{1}{2}(n+1)^{n} \text { term an } \frac{1}{2}(n+3)^{n} \text { term }\)

(7) Taking a = x and b = -y in the expansion, we get (x-y)ⁿ =[x + (-y)]ⁿ

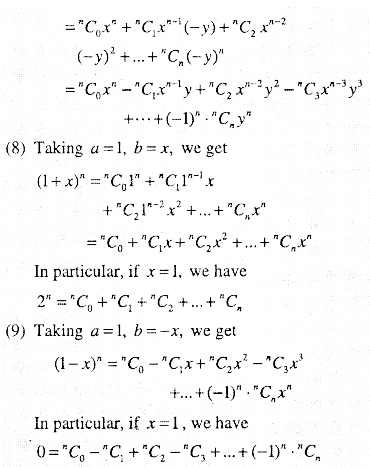
Question 2.
Expand each of the expression
(i)\(\left(x^{2}+\frac{3}{x}\right)^{4}\)
(ii)\((1-2 x)^{5}\)
(iii)\(\left(\frac{2}{x}-\frac{x}{2}\right)^{5}\)
(iv)\((2 x-3)^{6}\)
(v)\(\left(\frac{x}{3}+\frac{1}{x}\right)^{5}\)
(vi)\(\left(x+\frac{1}{x}\right)^{6}\)
Answer:

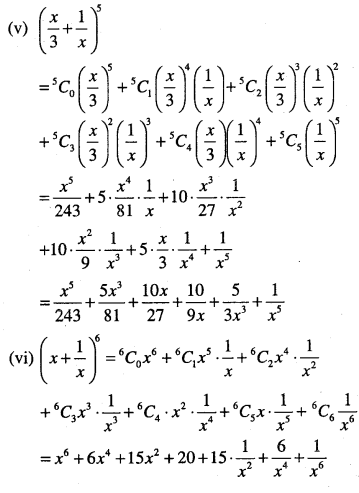
Question 3.
Using binomial theorem, evaluate each of the following:
(i) (98)⁵
(ii) (96)³
(iii) (102)⁵
(iv) (101)⁴
(v) (99)⁵
Answer:

Question 4.
Which is longer \((1.01)^{1000000} \text { or } 10,000 ?\)
Answer:

Question 5.
Using Binomial theorem, indicate which number is larger \( (1.1)^{10000} \text { or } 1000 ?\)
Answer:
Spilitting 1.01 and using Binomial theorem write the first few terms, we have.

Question 6.
Find (a + b)⁴ – (a -b)⁴. Hence evaluate
\((\sqrt{3}+\sqrt{2})^{4}-(\sqrt{3}-\sqrt{2})^{4}\)
Answer:

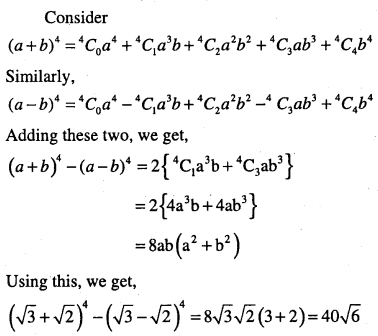
Question 7.
Find (x +1)⁶ +(x -1)⁶. Hence or otherwise evaluate
\((\sqrt{2}+1)^{6}+(\sqrt{2}-1)^{6}\)
Answer:

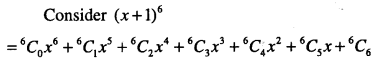
Question 8.
Evaluate:
\((\sqrt{3}+\sqrt{2})^{6}+(\sqrt{3}-\sqrt{2})^{6}\)
Answer:

Question 9.
Find the value of
\(\left(a^{2}+\sqrt{a^{2}-1}\right)^{4}+\left(a^{2}-\sqrt{a^{2}-1}\right)^{4}\)
Answer:

Question 10.
Show that 9ⁿ⁺¹ – 8n – 9 is divisible by 64, whenever ‘n’ is a positive integer.
Answer:

Question 11.
Using binomial theorem, prove that 6ⁿ -5n always leaves remainder 1 when
divided by 25.
Answer:

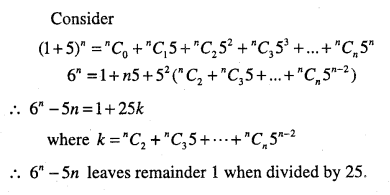
Question 12.
Prove that
\(\sum_{n=0}^{n} y \cdot c_{n}=4\)
Answer:

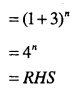
Question 13.
Find the 4^th term in the expansion of (x-2 y)¹².
Answer:

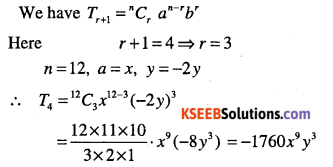
Question 14.
Find the 13^th term in the expansion of
\(\left(9 x-\frac{1}{3 \sqrt{x}}\right)^{18}, x \neq 0 \)
Answer:

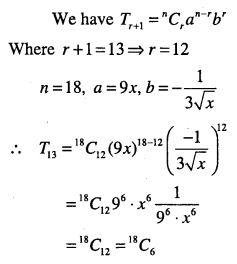
Question 15.
Write the general term in the expression of
(i) (x² -y)⁶
(ii) (x²-yx)¹²,x≠0
Answer:

Question 16.
Find the coefficient of
(i) x⁵ in (x + 3)⁸
(ii) a⁵b⁷ in (a – 2b)¹²
(iii) x⁶y³ in (x + 2y)⁹
Answer:

Question 17.
Find a, if the 17^th and 18^th terms of the expansion (2 +a)⁵⁰ are equal.
Answer:

Question 18.
In the expansion of (1+ a)^m+n, prove that coefficients of a^m and aⁿ are equal.
Answer:

Question 19.
Prove that the coefficient of xⁿ in the expansion of (1 + x)²ⁿ is twice the coefficient of xⁿ in the expansion of (1+x)^2n-1
Answer:
In (1+x)²ⁿ we have

From (1) and (2) we get, the coefficient of xⁿ in (1 + x)²ⁿ is twice the coefficient of xⁿ in (1 + x)^2n-1.

Question 20.
Find a positive value of m for which the coefficient of x² in the expansion (1 + x)^m is 6.
Answer:

Question 21.
Find the middle terms in the expansions of
(i) \(\left(3-\frac{x^{3}}{6}\right)^{7}\)
(ii)\(\left(\frac{x}{3}+9 y\right)^{10}\)
Answer:

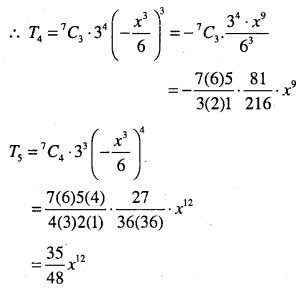
Question 22.
Show that the middle term in the expansion of \((1+x)^{2 n} \text { is } \frac{1 \cdot 3 \cdot 5 \ldots(2 n-1)}{\lfloor n} 2^{n} x^{n} \)where ‘n’ is a positive integer.
Answer:

Question 23.
The second, third and fourth terms in the binomial expansion (x + a)ⁿ are 240, 720 and 1080, respectively. Find x, a and n
Answer:

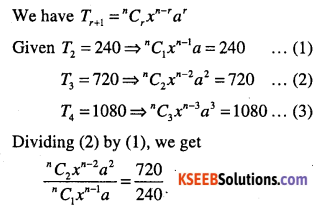
Question 24.
The coefficients of three consecutive terms in the expansion of (1 + a)ⁿ are in the ratio 1:7: 42. Find n
Answer:

Question 25.
The coefficients (r-1)^th, r^th,and (r + 1)^th, terms in the expansion of (x + 1)^th, are in the ratio 1:3:5. Find n and r.
Answer:

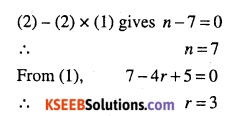
Question 26.
Find the term independent of x in the expansion of \(\left(\frac{3}{2} x^{2}-\frac{1}{3 x}\right)^{6}\)
Answer:

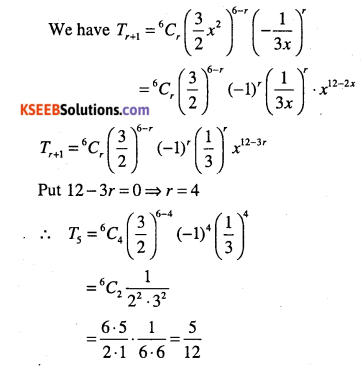
Question 27.
Find the term independent of x in the expansion of \(\left(\sqrt[3]{x}+\frac{1}{2 \sqrt[3]{x}}\right)^{18}, x>0\)
Answer:

Question 28.
Find a, 6 and n in the expansion of (a + b)ⁿ if the first three terms of the expansion are 729,7290 and 30375, respectively.
Answer:
Given: T_x = 729, T₂ = 7290 and T₃ = 30375
∴ aⁿ=729……………….(1)

Question 29.
Find a if the coefficients of x² and x³ in the expansion of (3 +ax)⁹ are equal.
Answer:

Question 30.
If the coefficients of (r – 5)^th and (2r -1)^th terms in the expansion of (1 + x)³⁴ are equal, find r.
Answer:

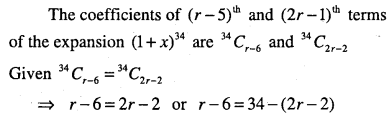
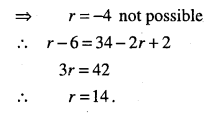
Question 31.
If the coefficients of a^r-1, a^r and a^r+1 in the expansion of (1 + a)ⁿ are in arithmetic progression, prove that n² – n(4r +1) + 4r² -2 = 0.
Answer:

Question 32.
Show that the coefficient of the middle term in the expansion of (1 + x)²ⁿ is equal to the sum of the coefficients of two middle terms in the expansion of (1 + x)^2n-1.
Answer:

Question 33.
Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of
\(\left(\sqrt[4]{2}+\frac{1}{\sqrt[4]{3}}\right)^{n} \text { is } \sqrt{6}: 1\)
Answer:

Question 34.
Find the r^th term from the end in the expansion of (x + a)ⁿ.
Answer:
r^th term from the end in (x + a)ⁿ

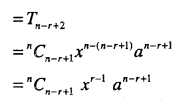
Question 35.
If a and b are distinct integers, prove that a-b is a factor of aⁿ -bⁿ, whenever n is a positive integer.
Answer:

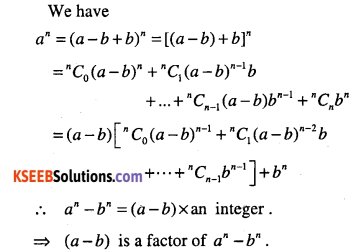
Question 36.
The sum of the coefficients of the first three terms in the expansion of
\(\left(x-\frac{3}{x^{2}}\right)^{m}, x \neq 0, m \)being a natural numbers, is 559. Find the term of the expansion containing x³.
Answer:

Question 37.
Find the coefficient of x⁵ in the product (1 + 2x)⁶(1 – x)⁷ using binomial theorem.
Answer:

Question 38.
Find the coefficient of a⁴ in the product (1 + 2a)⁴(2-a)^s using binomial theorem.
Answer:

Question 39.
Expand using Binomial theorem
\(\left(1+\frac{x}{2}-\frac{2}{x}\right)^{4}, x \neq 0\)
Answer:

Question 40.
Find the expansion of (3x² – 1ax + 3a²)³ using binomial theorem.
Answer: