You can Download Chapter 6 Work, Energy and Power Questions and Answers, Notes, 1st PUC Physics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 1st PUC Physics Question Bank Chapter 6 Work, Energy and Power
1st PUC Physics Work, Energy and Power TextBook Questions and Answers
Question 1.
State carefully
if the following quantities are positive or negative:
- work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
- work done by gravitational force ‘in the above case,
- work done by friction on a body sliding down an Inclined plane,
- work done by an applied force on a body moving on a rough horizontal plane with uniform velocity,
- work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Solution:
1. We know that: W = \(\overrightarrow{\mathrm{F}}, \overrightarrow{\mathrm{S}}\) = FS cos θ
‘Positive’
Reason: Force is acting in the direction of displacement (θ = 0°)
2. ’Negative’
Reason: Force is acting in the opposite direction to displacement (θ =180°)
3. ’Negative’
Reason: Force of friction is opposite to the displacement (θ = 180°)
4. ‘Positive’
Reason: The body mover in the direction of force applied (θ = 0°)
5. ‘Negative’
Reason: The resistive force opposes the motion (θ = 0°)
Question 2.
A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with a coefficient of kinetic friction = 0.1. Compute the
- work done by the applied force in 10 s
- work done by friction in 10 s
- work done by the net force on the body in 10 s
- change in kinetic energy of the body in 10 s, and interpret your results.
Solution:
1. We know that: μk\(\frac{\text { Frictional force }}{\text { Normal force }}\)
Here, μk =0.1 and
normal force = mg
Frictional force = 0.1 × 2 × 9.8 N = 1.96 N
∴ Net force = (7 – 1.96) N
= 5.04 N
acceleration = \(\frac{\text { Net force }}{\text { Mass }}\) = \(\frac{5.04}{2}\) m/s²
= 2.52 m/s
To find the distance (d) moved in 10 s
d = \(\frac{1}{2}\) × 2.52 × 10 × 10 = 126 m
∴ Work done by applied force in 10 s is work done = 7 × 126 J
= 882 J.
2. Work done by the friction in 10 ‘s’ we know that frictional force = 1.96 N
∴ work done by frictional force = 1.96 × 126
= 246.96 J.
Since force is opposite to the direction of displacement (0 = 180°), work done is = 246.96 J.
3. Work done by the Net force in 10 ‘s’
we know that Net Force = 5.04 N.
∴ work done by the Net force = 5.04 × 126 = 635.04 J.
4. Change in the body’s kinetic energy is the net work done on the body = work done by the Net force in 10’s’.
∴ Change in kinetic energy of the body = 635.04 J
![]()
Question 3.
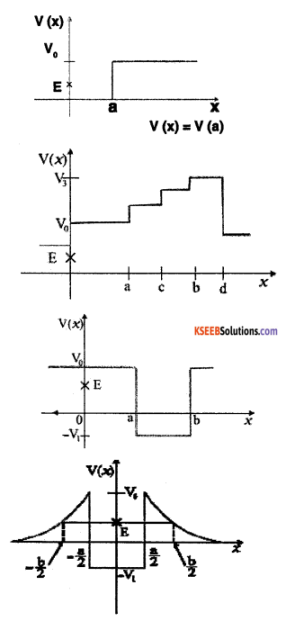
Given in Fig. 6 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, Indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
Solution:
(a) We know that Total energy E = KE + PE, kinetic energy can never be negative. In the region between x = 0 & x = a.
Potential energy is ‘0’. So, kinetic energy y is positive. In region x > a the potential energy has a value greater than ‘E’. So kinetic energy will be negative in this region. Hence the particle cannot be present in the region x > a.
(b) Here PE > E, the total energy of the object and as such the kinetic energy of the object would be negative. Thus object cannot be present in any region on the graph.
(c) Here x = 0 to x = a & x > b, the P E is more then E so, K E is negative. The particle cannot be present in these portions.
(d) The object cannot exist in the region between
x = \(\frac{-b}{2}\) to x = \(\frac{-a}{2}\) & x = \(\frac{-a}{2}\) to x = \(\frac{-b}{2}\)
Because in this region P E > E.
Question 4.
The potential energy function for a particle executing linear simple harmonic motion is given by V(x) = kx²/ 2, where k is the force constant of the oscillator. For k = 0.5 Nm-1, the graph of V(x) versus x is shown in figure Show that a particle of total energy 1 J moving under this potential must turn back when it reaches x = ± 2m
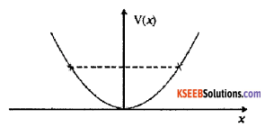
Solution:
Here force constant k = 0.5 Nm-1 and the total energy of particle E = 1 J. The particle can go up to a maximum distance of xm, at which its total energy transformed into elastic potential
energy. We know that , \(\frac{1}{2}\) Kxm² = E
![]()
Question 5.
Answer the following :
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?
(c) An artificial satellite orbiting the earth in a very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?
(d) In Fig. (i) the man walks 2 m carrying a mass of 15 kg on his hands.
In Fig. (ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?
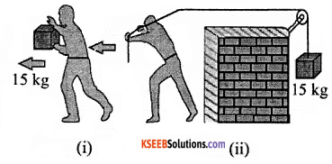
Solution:
(a) Heat energy required for the burning of the casing of a rocket is obtained by rocket. Since the work is done against the friction, the kinetic energy of rocket decreases continuously and this work against friction reappears as heat energy.
(b) This is because of the conservative nature of the gravitational force. Work done by the gravitational force in a closed path is zero.
(c) As an artificial satellite gradually loses its energy due to dissipation against atmospheric resistance, its potential decreases rapidly. As a result, the kinetic energy of satellite slightly increases i.e. its speed increases progressively.
(d) In fig (i) the force applied by the man is perpendicular to the direction of movement of mass, i.e. θ = 90°
W = Fs cos θ = Fs cos 90° = 0
In figure (ii) the force applied is in direction of the movement of mass i.e. θ = o°
∴ W = Fs cos θ = Mgs cos θ
= 15 × 9.8 × 2 × 1 = 294 J.
![]()
Question 6.
Point out the correct alternative:
- When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains same.
- Work done by a body against friction always results in a loss of its kinetic/potential energy.
- The rate of change of total momentum of a many-particle system is proportional to the external force/ sum of the Internal forces on the system.
- In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.
Solution:
- Potential energy decreases
- Kinetic energy
- External force
- Total linear momentum/total energy of two bodies.
Question 7.
State if each of the following statements is true or false. Give reasons for your answer.
- In an elastic collision of two bodies, the momentum and energy of each body is conserved.
- Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
- Work done in the motion of a body over a closed loop is zero for every force in nature.
- In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.
Solution:
- False, the momentum and energy of each body is conserved.
- False, the external force on the system may increase or decrease the total energy of the system.
- False, for the nonconservative forces (friction) the work done in closed loop is not zero.
- True, usually in an inelastic collision the final kinetic energy is always less than initial kinetic energy of the system.
Question 8.
Answer carefully, with reasons :
- In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
- Is the total linear momentum. conserved during the short time of an elastic collision of two balls?
- What are the measures to (a) and (b) for an inelastic collision?
- If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or Inelastic?
Solution:
- In this case total kinetic energy is not conserved because when the bodies are in contact during elastic collision even the kinetic energy is converted to potential energy.
- yes, because total momentum conserves as per the law of conservation of momentum.
- The answers are the same for an inelastic collision also.
- It is a case of elastic collision because in this case, the forces will be of conservative nature.
Question 9.
A body is initially at rest. It undergoes a one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
- t1/2
- t
- t3/2
- t2
Solution:
we know that v = u + at & u = 0 v = at and P = F × V
∴But F = ma
hence P = ma × at = ma2t .
Thus power is proportional to ‘t’.
Question 10.
A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to
- t1/2
- t
- t3/2
- t2
Solution:
It is proportional ‘t3/2’
We know that P = F × V
[P] = [F] [V]
[P] = [MLT-2] [LT-1] since ‘P’ & ‘M’ are constant.
L2T-3 = constants ⇒ \(\frac{L^{2}}{T^{3}}\)= constant.
L2 & T3 ⇒ L & T3/2
Question 11.
A body constrained to move along the z-axis of a coordinate system is subject to a constant force ‘F’ given
by \(\vec{F}=-\hat{i}+2 \hat{j}+3 \hat{k} N\).
What is the work done by the Force ‘F’ in moving the body 4m in the z-axis.
Solution:
\(\overrightarrow{\mathrm{S}}=4 \hat{\mathrm{k}}\), \(\overrightarrow{\mathrm{F}}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}\)
We know that W = FS cos e = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{S}}\)
W = \([-\hat{i}+2 \hat{j}+3 \hat{k}]\) . \([4 \hat{k}]\)
= 1 Joules.
Question 12.
An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV, and the second with 100 keV. Which is faster, the electron or the proton? Obtain the ratio of their speeds, (electron mass = 9.11 × 10-31 kg. Proton mass = 1.67 × 10-27kg. 1eV = 1.60 × 10-19J).
Solution:
Kelectron = 10 keV, Kproton = 10 keV
melectron = 9.11 × 10-31 kg and
mProton = 1.67 × 10-27 kg.
We know that K = \(\frac{1}{2}\) mv², v = \(\sqrt{\frac{2 k}{m}}\)
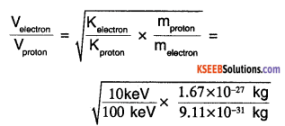
= 13.54
∴ \(\frac{V_{\text {electron }}}{V_{\text {proton }}}\) = 13.54
Electron is moving Faster.
Question 13.
A raindrop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until, at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its Journey? What is the work done by the resistive force in the entire journey if its speed on reaching the ground Is 10 ms-1?
Solution:
r = 2mm = 2 × 10-3 m
Distance moved half journey s = 250 m
we know that density of water,
ρ = 103 kg/m3
∴ mass of rain drop = volume × density
m = \(\frac{4 \pi r^{3} \rho}{3}\) = \(\frac{4}{3}\) × 3.14 × (2 × 10-3)3 × 103
m= 3.35 × 10-5 kg
∴ W = mgr = 3.35 × 10 5 × 9.8 × 250 = 0.082 J
∴ work done by gravitational force in first and second half is the same and is equal to 0.082 J. If there is no resistive forces, energy of the drop on reaching ground
E1 = mgr= 3.35 × 10-5 × 9.8 × 500
= 0.164 J
because of resistive force, the energy of the drop on reaching ground
E2 = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × 3.35 × 10-5 × 10²
= 1.675 × 10-3 J.
∴ work done by the resistive force is
W = E1 – E2 = 0.164 – 1.675 x 10-3
= 0.1623 J.
![]()
Question 14.
A molecule in a gas container hits a horizontal wall with speed 200 ms-1 and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?
Solution:
Let us consider the mass of the molecule be ‘m’ and that of the wall be ‘M’. The wall is at rest always. Resolving momentum of the molecule along x-axis and y-axis we get
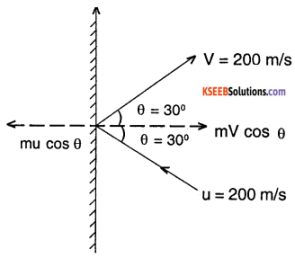
The x-component of momentum of molecule
mu cos θ = – m 200 cos 30° = -m\(100 \sqrt{3}\) kg m/s
y component of the molecule momentum is
= mu sin θ = m x 200 x sin 30° = m100kgm/s
Before collision:
x-component of total momentum = -100\(\sqrt{3}\) m
Y component of momentum = 100 m
After collision:
x component of the momentum = m 200 cos 30° = 100 \(\sqrt{3}\) m
Y component = m 100 sin 30° = 100 m
∴ It can be seen that momentum of system is conserved. The wall has a recoil momentum such that momentum of the wall + momentum of out going molecule equals the momentum of the incoming molecule.
Initial kinetic energy \(\left(\frac{1}{2} \mathrm{mu}^{2}\right)\) is the same as final KE \(\left(\frac{1}{2} m v^{2}\right)\) molecule.
∴ u = v = 200 m/s thus the collision is elastic collision.
Question 15.
A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m3 in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?
Solution:
Volume of water = 30m3
t = 15 min = 15 x 60 = 900 s
h = 40 m; η = 30%
we know that density of water
ρ =103 kgm-3
∴ mass of water pumped
m = volume x density = 30 x 103 kg
Actual power consumed
p0 =\(\frac{W}{t}\) = \(\frac{m g h}{t}\)
p0 = \(\frac{30 \times 10^{3} \times 9.8 \times 40}{900}\) = 13070 watt
If pi (required), then
n = \(\frac{\mathrm{p}_{\mathrm{o}}}{\mathrm{p}_{\mathrm{i}}}\) ⇒ pi = \(\frac{\mathrm{p}_{\mathrm{o}}}{\mathrm{n}}\) = \(\frac{13070}{0.3}\)
= 43567 w
Question 16.
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following (Figure) is a possible result after collision?
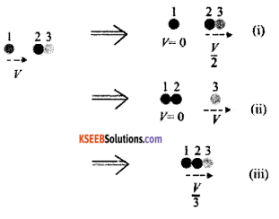
Solution:
Let m be the mass of each ball Total KE of the system before collision = \(\frac{1}{2}\)mv²
Total KE of the system after collision is
case (i) E1 = \(\frac{1}{2}\) (2m) \(\left(\frac{v}{2}\right)^{2}\) = \(\frac{1}{4}\)mv²
case (ii) E2 = \(\frac{1}{2}\)mv²
case (iii) E3 = \(\frac{1}{2}\)(3m) \(\left(\frac{v}{2}\right)^{3}\) = \(\frac{1}{6}\)mv²
∴ case (ii) is only possibility since KE of the system is conserved.
Question 17.
The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

Solution:
Since the collision is elastic ‘A’ will come to rest and ‘B’ will begin to move with velocity of ‘A’. The bob ‘A’ transfers its entire momentum to the bob ‘B’ on table. Thus bob ‘A’ does not rise at all.
Question 18.
The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?
Solution:
On releasing the bob of the pendulum from horizontal position, it falls vertically down ward by a distance equal to length of pendulum i.e. h = I = 1.5.m. As 5% of loss is P E is dissipated against air resistance, the balanic 95% energy is transformed into KE Hence,
\(\frac{1}{2}\)mv² = 0.95 x mgh
V = \(\sqrt{2 \times 0.95 \times 9.8 \times 1.5}\) = 5.3 ms-1.
Question 19.
A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km/h on a frictionless track. After a while, sand starts leaking out of a hole on the floor of the trolley at the rate of 0.05 kg s-1. What is the speed of the trolley after the entire sandbag is empty?
Solution:
The system of trolley and sandbag is moving with a uniform speed. Clearly, the system is not being acted upon by the external force. If the sand leaks out, even then no external force acts. So there shall no change in the speed of the trolley.
Question 20.
A particle of mass 0.5 kg travels in a straight line with velocity v = a x3/2 where a = 5 m-1/2s-1. What is the work done by the net force during its displacement from x = 0 to x = 2 m?
Solution:
Given m = 0.5 kg.
V = ax3/2, a = 5m-1/2 s-1
initial velocity at x = 0, v1= a × 0 = 0
Final velocity at x = 2n is,
V2 = a (2)3/3 = 5 × 23/2
work done = change in KE
\(\frac{1}{2}\) m (v2² – v1²) = \(\frac{1}{2}\) × 0.5 × 25 × 23
= 50 J .
![]()
Question 21.
The blades of a windmill sweep out a circle of area A.
- If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time?
- What is the kinetic energy of the air?
- Assume that the windmill converts 25% of the wind’s energy into electrical energy and that A = 30 m², v = 36 km/h and the density of air is 1.2 kg m-3. What is the electrical power produced?
Solution:
1. Volume of the wind flowing per sec = AV
Mass of wind flowing per sec = AVP
Mass of air passing in sec = AVPt
2. Kinetic energy of Air
= \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) (Avpt)v²
= \(\frac{1}{2}\)Av3pt
3. Electrical energy produced =
\(\frac{25}{100}\) × \(\frac{1}{2}\)Av3pt = \(\frac{\mathrm{Av}^{3} \mathrm{pt}}{8}\)
Electrical power = \(\frac{\mathrm{Av}^{3} \mathrm{p}}{8 \mathrm{t}}\) = \(\frac{A V^{3} p}{8}\)
Now, A = 30m2,
v = 36 kmh-1 = \(\frac{36 \times 100}{3600}\) m/s = 10ms-1
ρ = 1.2 Kgms-1
Electrical power =
\(\frac{30 \times 10^{3} \times 1.2}{8}\) = 4500 W = 4.5kW.
Question 22.
A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated.
- How much work does she do against the gravitational force?
- Fat supplies 3.8 × 107J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up?
Solution:
Here, m = 10kg, h = 0.5m, n = 1000
1. Work done against gravitational force w = n (mgh) = 1000 × 10 × 9.8 × 0.5 = 49000 J.
2. Mechanical energy supplied by 1 kg of fat = 3.8 × 107 × \(\frac{20}{100}\) = 0.7 × 107 J/kg
∴ Fat used up by the dieter = \(\frac{1 \mathrm{kg}}{0.7 \times 10^{7}}\) × 49000 = 6.45 × 10-3kg
Question 23.
A family uses 8 kW of power.
- Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW?
- Compare this area to that of the roof of a typical house.
Solution:
1. Power used by family, p = 8kW= 8000 W
As only 20% of solar energy can be converted to useful electrical energy, power to be supplied by solar energy =
\(\frac{8000 w}{20 \%}\) = 40000 w.
Solar energy is incident at a rate of 200 w/m² hence Area needed.
A = \(\frac{4 \mathrm{0} \mathrm{00w}}{200 \mathrm{Wm}^{-2}}\) = 200 m².
2. The area needed is comparable to roof area of large sized house.
Question 24.
A bullet of mass 0.012 kg and horizontal speed 70 ms-1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
Solution:
m1 = 0.012 kg, u1 = 70ms-1
m2 = 0.4 kg, u2 = 0.
After the collision the bullet strikes in the block and both behave as a single body of mass m1 + m2 and moves with velocity V.
By conservation of momentum (m1 + m2) v = m1u1 + m2u2
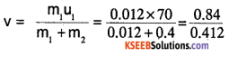 = 2.04 ms-1
= 2.04 ms-1
Let the block move to a height ‘h’
(m1 + m2)gh = \(\frac{1}{2}\) (m1 + m2) v²
h = \(\frac{\mathrm{v}^{2}}{2 \mathrm{g}}\) = \(\frac{2.04 \times 2.04}{2 \times 9.8}\) = 0.212 m
To find the heat produced, calculate energy lost (w)
w = initial KE of bullet – final KE of combination
= \(\frac{1}{2}\) m1 u1² – \(\frac{1}{2}\) (m1 + m2) v²
= \(\frac{1}{2}\) x 0.012(70)² – \(\frac{1}{2}\) (0.412) (2.04)²
w = 29.4 – 0.86 = 28.5 J
∴ Heat produced
H = \(\frac{\mathrm{w}}{\mathrm{j}}\) = \(\frac{28.54}{4.2}\) = 68 cal.
Question 25.
Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track. Will the stones reach the bottom at the same time? Will they reach there with the same speed? Explain. Given θ1 = 30°, θ2 = 60°, and h = 10 m, what are the speeds and times taken by the two stones?
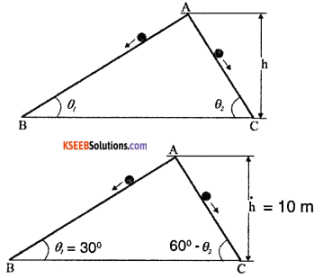
Solution:
Assume the two stones are rest at the point ‘A’ & allowed to roll down. Since the height is same for the both the stones, the velocity at which they reach ground will be same given mass of both stones are equal.
i.e. \(\frac{1}{2}\) mV² = mgh V = \(\sqrt{2 \mathrm{gh}}\)
VB = Vc = \(\sqrt{2 \times 10 \times 10}\) = 14.14 ms-1
we know that H = l sin θ, l = \(\frac{\mathrm{h}}{\sin \theta}\)
and the acceleration at which they roll is a = g sin θ.
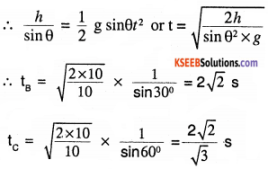
Question 26.
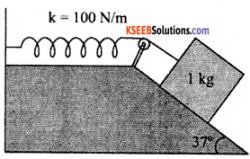
A 1 kg block situated on a rough incline is connected to a spring constant 100Nm-1. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline.
Solution:
The normal reaction force of block on incline R = mg cos θ
Let the coefficient of friction be M
∴ F = MR
= μ mg cos θ
∴ Net force on block = mg sin θ – F
= mg (sin θ – μ cos θ )
we know that the block moves by distance x = 10cm = 0.1 m.
The work done by net force in moving block 0.1m is = Energy stored in the spring.
∴ mg (sin θ – μ cos θ) x = \(\frac{1}{2}\) kx²
∴ 2 mg (sin 37° – μ cos 37°) = kx
⇒ 2 × 1 × 9.8 ms-2(sin37°- μ cos37°) = 100 × 0.1m
⇒ 19.6 (0.601 – μ × 0.798) = 10
0.601 – μ × 0.798 = 0.5102
⇒ μ × 0.798 = 0.09079
∴ μ = \(\frac{0.09079}{0.798}\) = 0.1137.
![]()
Question 27.
A bolt of mass 0.3 kg falls the celling of an elevator moving down with a uniform speed of 7ms-1. It hits the floor of the elevator (length of elevator = 3m) and does not rebound. What is the heat produced by the impact? Would your answer be different if the elevator were stationary?
Solution:
Potential energy of bolt = mgh = 0.3 × 9.8 × 3 = 8.82 J.
Since the bolt does not rebound, the while energy is converted into heat. Since the value of acceleration due to gravity is the same in all inertial systems, the answer will not change even if the elevator is stationary.
Question 28.
A trolley of mass 00 kg moves with a uniform speed of 36 km h-1 on a frictionless track. A child of mass 20 kg runs on a trolley from one and to the other (10m away) with a speed of 4ms-1 relative to the trolley in a direction opposite to the trolley’s motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
Solution:
Let there be an observer traveling parallel to the trolley at the same speed. He will observe the initial momentum of the trolley of mass M and the child of mass m as zero. When the child jumps in the opposite direction, he will observe the increase in the velocity of the trolley by ΔV.
Let u be the velocity of the child. He will observe child landing at velocity (u – ΔV )
Therefore, initial momentum = 0
Final momentum = M ΔV – m (u – ΔV )
Hence, M ΔV – m (u – ΔV ) = 0
∴ ΔV = \(\frac{\mathrm{mu}}{\mathrm{M}+\mathrm{m}}\) = \(\frac{4 \times 20}{20+220}\) = 0.36 m/s
∴ final speed of trolley is 10.36 ms-1 and child take 2.5s to run on trolley.
∴ trolley moves a distance of 2.5 × 10.36
= 25.9 m.
Question 29.
Which of the following potential energy curves in Figure cannot possibly describe the elastic collision of two billiard balls? Here r is the distance between the centres of balls.
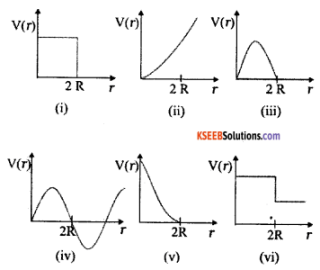
Solution:
The potential energy of a system of two masses varies inversely as the distance (r) between them i.e.
V(r) < \(\frac{1}{r}\) When the two balls touch each other, PE becomes zero i.e. at r – R + R = 2R , v (r) = 0. Out of the given graphs only the curve (V) satisfies these two conditions.
1st PUC Physics Work, Energy and Power One Mark Questions and Answers
Question 1.
What is the significance of the negative sign in w = – mgh.
Answer:
A negative sign signifies that the work is done against the gravitational force.
Question 2.
Is friction a conservative force? Give reason.
Answer:
No, because work done in a closed path against friction is not zero. Moreover, and the work done against fiction depends on the path.
Question 3.
Give the conditions under which a force is called a conservative force.
Answer:
A force is called to be a conservative force,
- work done against the force has to be independent of the path.
- work done against the force in a closed path has to be zero.
Question 4.
A mass m collides with the other mass m and sticks to it. What Is the nature of collision?
Answer:
Whenever a mass collides and sticks to other mass, the nature of collision is inelastic.
Question 5.
What is the relation between ergs and joule?
Answer:
1 Joule = 107 ergs.
Question 6.
A mass is moving is a circular path with a constant speed. What is the work done on 1/2th of the rotation?
Answer:
Work done is zero, since centripetal force and displacement are perpendicular to each other.
![]()
Question 7.
A light body and a heavy body have same momentum. Which one will have greater kinetic energy?
Answer:
We know that KE = \(\frac{p^{2}}{2 m}\),
given p is same ∴ k E α \(\frac{1}{2 m}\)
∴ Lighter body will have greater kinetic energy.
Question 8.
A spring is cut into equal halves. How is spring constant of each half affected?
Answer:
We know that F α l
i.e. F = k l
∴ For a given force, k α \(\frac{1}{\ell}\) since extension a length. If length is halved then the spring constant doubles.
Question 9.
Does a single external force on a particle necessarily change its kintetic energy?
Answer:
Yes, a single external force cannot keep the particle is equilibrium.
Question 10.
What is the work done by earth’s gravitational force in keeping the moon in its orbit?
Answer:
Work done is zero since force and displacement are in perpendicular direction, i.e. w = o.
Question 11.
Define ‘work’.
Answer:
Work is said to be done if the body is displaced by the application of force.
Question 12.
Write the dimensional formula of work.
Answer:
ML2T-2
Question 13.
What is the work done when the displacement is perpendicular to the force applied.
Answer:
Zero.
Question 14.
Define one Joule.
Answer:
Work done is said to be 1 joule, if a force of 1 newton displaces a body through 1 meter in the direction of force.
![]()
Question 15.
What does the area under the force displacement curve indicate?
Answer:
The area under the force displacement curve indicates the work done.
Question 16.
Define energy.
Answer:
The energy of a body is its capacity to do work.
Question 17.
State the law of conservation of energy.
Answer:
Energy can neither be created nor be destroyed, but can only be converted from one form to another, i.e., The total energy of a closed system remains constant.
Question 18.
Define power.
Answer:
Power is the rate of doing work.
Question 19.
What is the unit of power?
Answer:
Watt.
Question 20.
Write the dimensional formula of power.
Answer:
ML2T-3
Question 21.
Write an expression for instantaneous power in terms of force and velocity.
Answer:
Instantaneous power = Force × uniform velocity.
Question 22.
State work-energy theorem.
Answer:
The work-energy theorem states that the work done on a body is equal to the change in its kinetic energy.
Question 23.
What is a conservative force?
Answer:
A force is said to be conservative if the work done by the force does not depend on path followed by the body but depends only on the initial and final positions of the body.
Question 24.
What is an elastic collision?
Answer:
An elastic collision is the one in which both kinetic energy and momentum are conserved.
Question 25.
Define coefficient of restitution. Write an expression for it?
Answer:
Coefficient of restitution is defined as the ratio of relative velocity after collision to the relative velocity before collision. If u1 & u2 are the velocities of 2 bodies before collision & v1 & v2 are velocities after collision then coefficient of restitution
e = \(\frac{v_{1}-v_{2}}{u_{1}-u_{2}}\)
Question 26.
Write the S.l unit of work.
Answer:
The S. I unit of work is joule.
![]()
Question 27.
Give an example for conservative force
Answer:
Gravitational force.
Question 28.
What is the value of the coefficient of restitution in case of a perfectly inelastic collision?
Answer:
e = 0.
Question 29.
Name any one form of energy.
Answer:
Kinetic energy.
1st PUC Physics Work, Energy and Power Two Marks Questions and Answers
Question 1.
What are conservative forces? Distinguish the conservative and nonconservative forces among the following:
- Gravitational force
- Frictional force
- Air resistance
- Electrostatic force
Answer:
Conservative forces are those forces in which work done
1. in a closed path is zero and
2. is independent of path.
| Conservative Forces | Non Conservative Forces |
| Gravitational force Electrostatic force | Frictional force Air resistance |
Question 2.
Two masses 10kg and 20 kg are connected by a massless spring. A force of 200 N acts on 20 kg mass. At the instant when the 10 kg mass has an acceleration 12 ms-2, what will be the energy stored in the spring? k = 2400 M/m

Answer:
We know that F = ma
F = 10 × 12 = 120 N
But F = k x = 2400 x = 120 n
∴ x = \(\frac{1}{20}\)
∴ energy stored in spring
E = \(\frac{1}{2}\) kx2 = \(\frac{1}{2}\) × 2400 × \(\left(\frac{1}{2}\right)^{2}\) = 3J
Question 3.
How are fast neutrons slowed down with the use of moderators?
Answer:
Neutrons from stable nuclei with proton. Protons available in heavy water mix with neutron. Since their masses are comparable, the neutrons come to rest in the collision.
Question 4.
A body of mass 4kg initially at rest is subjected to a force 16 N. What is the kinetic energy acquired by the body at the end of 10s?
Answer:
Given m = 4kg, u = 0
F = 16 N, t = 10 s F = ma
16 = 4a, a = 4ms-2
We know that V = u + at = 0 + 4 × 10
V = 40ms-1
![]()
Question 5.
What is the amount of work done by
- a weight lifter in holding a weight of 10 kg on his shoulder for 30 s, and
- a locomotive against gravity, if it is traveling on a level plane?
Answer:
- zero
- zero
Question 6.
A body of mass ‘M’ at rest is struck by a body of mass ‘m’. Show that the fraction of KE of mass m transferred to the struck particle is \(\frac{4 \mathrm{m} \mathrm{M}}{(\mathrm{m}+\mathrm{M})^{2}}\)
Answer:
m1 = m, u1 = u
m2 = M, u2 = 0 V2 = ?
By conservation of momentum
m1 u1 = (m1 + m2) v2
∴ v2 = \(\frac{\mathrm{m}_{1} \mathrm{u}_{1}}{\mathrm{m}_{1}+\mathrm{m}_{2}}\)
k E of body struck after collision
E2 = \(\frac{1}{2}\) m2v2² = \(\frac{1}{2}\)m \(\left(\frac{2 m u}{m+M}\right)^{2}\)
= \(\frac{2 \mathrm{Mm}^{2} \mathrm{U}^{2}}{(\mathrm{M}+\mathrm{m})^{2}}\)
Initial K E E1 = \(\frac{1}{2}\) m1 u1² = \(\frac{1}{2}\) mu²
∴ Fraction of initial K E transferred is
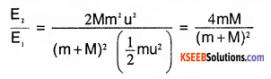
Question 7.
How high must a body be lifted to gain an amount of potential energy equal to the kinetic energy it has. When moving at sped 20ms-1. The value of acceleration due to gravity at that place is g = 9.8 ms-2
Answer:
mgh = \(\frac{1}{2}\) mv²
i.e. 9.8 h = \(\frac{1}{2}\) × 20 × 20
h = \(\frac{200}{9.8}\) = 20.4 m.
Question 8.
Define kinetic energy. Give an example of a body possessing kinetic energy.
Answer:
The energy possessed by a body due to its motion is called kinetic energy. A bullet fired from a gun can penetrate a target due to its kinetic energy.
Question 9.
Explain potential energy with example.
Answer:
The energy possessed by a body due to its position or configuration is called potential energy. example: The potential energy of water in dams is used to run turbines in order to produce electrical energy.
Question 10.
Derive an expression for gravitational potential energy.
Answer:
Consider a body of mass ‘m’ lying on the surface of earth. Force required to lift the body is equal to its weight mg. Let it be lifted through a height h. Work done on the body W = Fs = mgh This work done is stored in the body as its potential energy
Ep = mgh.
Question 11.
What is a non-conservative force? Give an example.
Answer:
A force is said to be non-conservative if the work done by the force depends on the path followed by the body, example: Frictional force, Air resistance, Viscous force.
Question 12.
Give an example of a body possessing potential energy and kinetic energy.
Answer:
Freely falling body possess both potential & kinetic energy.
Question 13.
The momentum of a body is increased twice; How does its Kinetic energy change?
Answer:
The Kinetic energy increases by four times.
Question 14.
Write the expression for the kinetic energy of a moving body and explain the symbols.
Answer:
Kinetic energy E = \(\frac{1}{2}\)(mv2)
m → mass of the body
v → velocity of the body.
1st PUC Physics Work, Energy and Power Three Marks Questions and Answers
Question 1.
A stone is dropped from a height ‘h’ prove that the energy at any point in its path is mgh.
Solution:
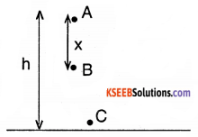
PE at ‘A’ = mgh
K E at ‘A’ = 0
∴ Total energy at A = mgh
As it starts falling at reaches the point ‘B’ it would have lost some PE and gained some KE.
we know that v² = u² + 2as
∴ V²B = 0 + 2g x
∴ VB = \(\sqrt{2 g x}\)
PE at B = mg (h – x)
KE at B = mgx
∴ Total energy at B = mgh – mgx + mgx = mgh.
On reaching the ground ‘C” the mass must have gained velocity of Vc =\(\sqrt{2 g h}\)
∴ PE at C =0
KE at C = mgh
∴ Total energy at C is mgh
Thus it is proved that the total energy at any point in its path is mgh.
![]()
Question 2.
A body of mass 3 kg makes an elastic collision with another body at rest and continues to move in the original direction with a speed equal to \(\frac{1}{3}\) rd of
its original speed. Find the mass of the second body.
Solution:
Given,
m1 = 3 kg, u1 = xms-1, v1 = \(\frac{x}{3}\) ms-1
m2 = mkg, u2 = 0
Since collision is elastic, both momentum and KE is conserved.
By conservation of momentum;
m1 u1 + m2 u2 = m1 v1 + m2 v2
3x + 0 = \(\frac{3 x}{3}\) + mv2
∴ 2x = mv2 ……………. (1)
By law of conservation of KE
\(\frac{1}{2}\) m1u1² + \(\frac{1}{2}\) m2u2² = \(\frac{1}{2}\) m1 v1² + \(\frac{1}{2}\) m1 v1²
\(\frac{1}{2}\) 3x² = \(\frac{1}{2}\) × 3 × \(\frac{x^{2}}{9}\) + \(\frac{1}{2}\) mv2²
3x² – \(\frac{x^{2}}{3}\) = m2v2²
m2v2² = \(\frac{8 x^{2}}{3}\)
Dividing 2 by 1, v2 = \(\frac{4 x}{3}\)
∴ from (1) m × \(\frac{4 x}{3}\) = 2x
∴ m = \(\frac{3}{2}\) kg = 1.5 kg
Question 3.
A block of mass 2kg is pulled up on a smooth incline of angle 30° with horizontal. If the block moves with an acceleration of 1ms-2, find the power delivered by the pulling force after 4 seconds. What is the average power delivered during these four seconds?
Solution:
Resolving the forces parallel to incline.
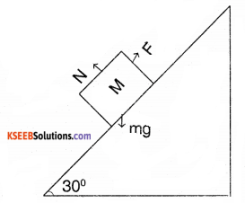
F – mg sin θ = ma.
F = mg sin θ + ma
= 2 × 9.8 × sin 30 + 2 × 1
= 11.8 N.
The velocity after 4 seconds = u + at.
= 0 + 1 × 4
= 4 ms-1
Power delivered by force at t = 4 sec
= Force × velocity
= 11.8 N × 4ms-1
= 47 .2 W
The displacement during 4 sec
V² = u² + 2as
16 = 2S
S = 8M
Work done in 4 sec = F × s = 11.8 × 8
= 94.4 J
∴ Average power delivered = \(\frac{\text { work done }}{\text { time }}\) = \(\frac{94.4}{4}\)
= 23.6 W.
Question 4.
The displacement x of a particle moving in one dimension under the action of a constant force is related to time by t = \(\sqrt{x}+3\) Where x is in meter & t in sec. Calculate the work done by the force in the first 6 seconds.
Solution:
Given t = \(\sqrt{x}\) + 3
\(\sqrt{x}\) = t – 3
∴ x = (t – 3)²
The velocity of the particle given by
V = \(\frac{d x}{d t}\) = 2(t – 3) ms -1
∴ The acceleration of the particle given by
a = \(\frac{d v}{d t}\) = 2 ms-2
Force required to produce this acceleration is given F = ma = m × 2 = 2m
Where ‘m’ is the mass of the particle. Distance travelled by the particle in first 6 sec.
x = (6 – 3)² = 9 m
∴ Hence work done = F × x = 2m × 9
= 18 m Joule.
Question 5.
An inclined plane (θ) has its topmost point at a height ii. Prove that the work done to bring a mass to the ground level either vertically or along the inclined surface is equal and is mgh. Also, prove that the velocity of the mass at the lowermost point is \(\sqrt{2 \mathrm{gh}}\)
Solution:
Consider path (a)
a = g sin θ
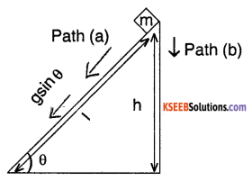
velocity on reaching ground is
V² = u² + zal
V² = 2 gsin θ l
where l = \(\frac{\mathrm{h}}{\sin \theta}\)
v = \(\sqrt{2 g \sin \theta \frac{h}{\sin \theta}}\) = \(\sqrt{2 g h}\)
work done = change in K E
= \(\frac{1}{2}\) mv² – 0 = \(\frac{1}{2}\) x 2gh x m = mgh
Consider Path (b)
a = g
velocity on reaching ground is
v² = u² + 2gh
v² = 2gh
v = \(\sqrt{2 g h}\)
work done = change in K E.
\(\frac{1}{2}\) mv² = mgh.
Question 6.
Define Elastic and Inelastic collisions. What are their basic characteristics?
Solution:
Elastic collision:
A collision in which there is absolutely no loss Of kinetic energy is called elastic collision.
Characteristics:
- The linear momentum is conserved
- Total energy of the system is conserved
- Kinetic energy is conserved
- Forces involved during elastic collisions must be conservative forces.
Inelastic collision:
A collision in which there is some loss of kinetic energy is called inelastic collision.
Characteristics:
- Linear momentum is conserved
- Total energy is conserved
- K E is not conserved
- Some or all forces involved may be nonconservative.
Question 7.
Derive an expression for the kinetic energy of a body.
Solution:
Consider a body of mass ‘m’ at rest. Let a constant force F act on the body producing an acceleration ‘a’ for a distance ‘s’. Let the velocity of the body be changed to v.
In this case, initial velocity = 0
final velocity = v.
Using, v² = u² + 2as
v² = 0 + 2as
v² = 2as
s = \(\frac{v^{2}}{2 a}\)
Work done F × s
= m a s = ma \(\frac{v^{2}}{2 a}\)
Work done = \(\frac{1}{2}\) mv²
By definition this work done is equal to the kinetic energy.
∴ kinetic energy of the body, Ek = \(\frac{1}{2}\) mv².
![]()
Question 8.
Distinguish between potential and b kinetic energy.
Solution:
1. potential energy is the energy possessed by a body due to its position or configuration while kinetic energy is the energy possessed by a body due to its motion.
2. Gravitational potential energy is given by Ep = mgh, but kinetic energy is Ek = \(\frac{1}{2}\) mv².
3. Potential energy is measured by the amount of work that a body can do when it returns to the standard position. Kinetic energy is measured by the work done on the body to change its velocity.
4. A wound spring has potential energy while a bullet fired from a gun has kinetic energy.
Question 9.
State and prove the work-energy theorem.
OR
Show that work done by a moving body is equal to the change in K.E. of the body.
Solution:
The work energy theorem states that work done on a body is equal to the net change in its energy. (P.E or K.E)
Proof:
Consider a body of mass ‘m’ moving with an initial velocity u. Let a constant force F acting on a body changes its velocity to v. Let s be the distance traveled.
From the equation, v² = u² + 2as,
we get v² – u² = 2as
\(\frac{1}{2}\) (v² – u²) = as
Multiplying both sides by m,we have
\(\frac{1}{2}\) m(v² – u²) = mas
\(\frac{1}{2}\) m(v² – u²) = F.s(∵ F = ma)
or \(\frac{1}{2}\) mv² – \(\frac{1}{2}\) mu² = W
Question 10.
Define potential energy. Derive an expression for gravitational potential energy. Mention its unit.
Solution:
The energy possessed by a body due to its position or configuration is called potential energy. Consider a body of mass ‘m’ lying on the surface of the earth. Force required to lift the body is equal to its weight
∴ F = mg
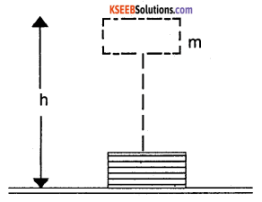
Let it be lifted through a height ‘h’
The work done on the body is W = FS
W = mgh (∵ S = h)
This work done is stored in the body as its potential energy
∴ Ep = mgh
i.e. Gravitational potential energy = mgh
Its unit is Joule.
Question 11.
State law of conservation of energy. Explain the conservation of energy in the case of a body sliding down on an inclined plane.
Solution:
The law of conservation of energy states that “ Energy is neither created nor destroyed. But it can be transformed from one from to another’’
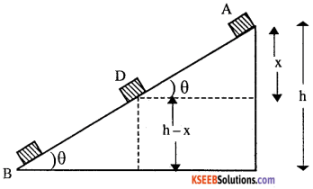
Consider a body of mass ‘m’ sliding down a smooth inclined plane of angle q and vertical height h. At the highest point A the body has only potential energy. Since it is at rest, kinetic energy is zero.
Total energy at A
= Potential Energy + Kinetic energy
= mgh ……………… (1)
Let the body slides down to a point D. Then it has both potential energy and kinetic energy. Let ‘x’ be the vertical distance travelled by the body.
∴ Potential energy at D is = mg (h – x) its velocity at D is v² = u² + 2as
v² = 0 + 2gsin θ. (AD)
(∵ u = 0, a = gsin θ, s = AD)
= 2g \(\frac{x}{A D}\) × AD
∵ sin θ = \(\frac{x}{A D}\) ∴ v² = 2gx
Kinetic energy of the body
= \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) m. (2gx) = mgx
Total energy at D is = mg (h -x) + mgx
= mgh …………. (2)
At the lowest point B, potential energy = 0
Kinetic energy = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) m. (2gh)
∵ v² = u² + 2as = 0 + 2gsin θ. (AB)
= 2g \(\frac{h}{A B}\) × AB = 2gh ∵ sin θ = \(\frac{h}{A B}\)
Kinetic energy = mgh
∴ Total energy = 0 + mgh = mgh …………… (3)
From (1), (2) and (3) it follows that total energy of the body remains constant while sliding down a inclined plane. Hence the principle.
1st PUC Physics Work, Energy and Power Five Marks Questions and Answers
Question 1.
A hammer of mass M drops from height ‘h’. It strikes a rail placed vertically on the ground and drives it. Into the ground through distance D. Calculate
- The average resistance offered by the ground, assuming that the hammer and rail remain stuck together after impact,
- The time for which the rail is in motion and
- The loss in kinetic energy in input.
Solution:
The hammer of mass M falls freely under the gravity through a distance. Let v be the speed acquired by the hammer when it strikes the rail obviously.
v = \(\sqrt{\mathrm{gh}}\) ………… (1)
On impact, the hammer and rail are stuck together. Let v be the speed of the combination after impact. The law of conservation of momentum gives.
Mv = (M + m) v1 …………….. (2)
Where m is the mass of the rail.
Let FG be the average resistance (or resistive force) exerted by the ground. The net upward force F on the hammer rail combination is
F = FG – (M + m)g.
The combination moves through a distance ‘d’ against this net upward force. Obviously, the work done against the force F in a distance ‘d’ must equal to the kinetic energy the combination had just after impact.
![]()
= [FG – (M + m) g] × d …………… (3)
By equations (1) & (2), we can rewrite equation (3) as

2. Let the hammer rail combination be moving for a time Δt, before coming to rest. If ΔP is the change in momentum,
\(\frac{\Delta p}{\Delta t}\) = FG – (M + m)g
\(|\Delta p|\) = (M + m) v1 – 0

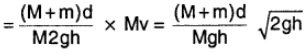
3. The kinetic energy of the hammer rail mcombination just before the impact is \(\frac{1}{2}\)
Mv² and after impact, it is ![]()
Loss in kinetic energy = \(\frac{1}{2}\) Mv² – \(\frac{1}{2}\)
Question 2.
A small block of mass m slides along the frictionless loop-to-loop track shown in the figure
- If it starts from rest at P, what is the resultant force acting on it at Q?
- At what height above the bottom of the loop should the block be released so that the force it exerts against the track at the top of the loop equal its weight?
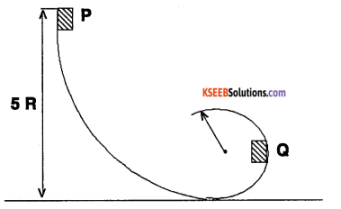
Solution:
1. Point Q is at a height R above the ground. Thus, the difference in height between points P & Q is 4 R. Hence the difference in gravitational potential energy of the block between these points is 4 mg R. Since the block starts from rest at P its kinetic energy at Q is equal to its change in potential energy. By the conservation of energy.
\(\frac{1}{2}\) mv² = 4 mg R
v² = 8g R
At Q, the only forces acting on the block are its weight ring acting downward and the force M of the track on block acting in radial direction. Since the block is moving in a circular path, the normal reaction provides the centripetal force for circular motion.
N = \(\frac{m v^{2}}{R}\) = \(\frac{\mathrm{m} \times 8 \mathrm{g} \mathrm{R}}{\mathrm{R}}\) = 8 mg
The loop must exert a force on block equal to eight times the blocks weight.
2. For the block to exert a force equal to its weight against the track at the top of the loop,
\(\frac{m v^{2}}{R}\) = 2 mg
or v2 = 2gR

The block must be released at a height of 3 R above the bottom of the loop.
Question 3.
A bullet of mass ‘m’ moving with a velocity V is embedded into a block of mass ‘x’ suspended by a thread. As a result of this collision the block along with the bullet rises to a height ‘h’ Prove that velocity of bullet was
\(\left(\frac{m+M}{m}\right) \sqrt{2 g h}\)
Solution:
let v1 be velocity of the system of block and the bullet. Applying principle of conservation of linear momentum, (M + m) v1 = mv
v1 = \(\frac{\mathrm{mv}}{(\mathrm{M}+\mathrm{m})}\) ………. (1)
As K E of the system = P E of the system at height ‘h’
\(\frac{1}{2}\) (m + M) v1² = (m + M) gh
V1 = \(\sqrt{2 \mathrm{gh}}\)
From (1)
v = \(\frac{(m+m) v_{1}}{m}\) = \(\frac{(m+M) \sqrt{2 g h}}{m}\)
Question 4.
A block of mass 200 g is released from ‘P’. if it slides down without friction till it reaches a point Q of traversing a circular path of radius 2.0 m.
- Find the velocity of the block at point Q and
- The coefficient of friction if the block comes to rest 2.0 m. from Q, Assuming the horizontal part of the path is rough. Take g – 10ms-2.
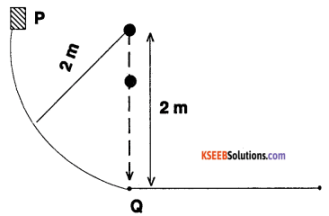
Solution:
1. P E of the block at P = kintetic energy of block at Q
∴ mgh = \(\frac{1}{2}\) mv²
v = \(\sqrt{2 g h}\) = \(\sqrt{2 \times 10 \times 2}\) = \(\sqrt{40 \mu}\) ∴ θ
= 6.32 ms -1.
2. When the block comes to rest after travelling a distance, r = 2m from then, work done against friction = change in K E
μ mgs = \(\frac{1}{2}\) mv²
∴ μ = \(\frac{v^{2}}{2 g r}\) = \(\frac{40}{2 \times 10 \times 2}\) = 1
Question 5.
A mass ‘m’ moving with a speed u colloids with a similar mass m at rest, elastically and obliquely. Prove that they will move in directions making an angle \(\frac{\pi}{2}\) with each other.
Solution:
Since momentum is a vector, the component along the x-axis and y-axis must separately balance each other.
On considering the components along the x-axis we have,
mu = mv1 cosθ1 + mv2cosθ2
i.e. u = v1 cosθ1 + v2 cos θ2 …………………. (1)
Similarly on considering the components along the y-axis we have,
0 = v1 sin θ1 + v2 cos θ2 ……………… (2)
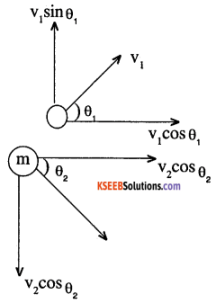
Being an elastic collision, kinetic energy is also conserved.
\(\frac{1}{2}\)mu² = \(\frac{1}{2}\) mv1² + \(\frac{1}{2}\) mv2²
u² = v1² + v2² ………………. (3)
squaring & adding (1) and (2) we get
u² = v1² + v2² + 2 v1v2 + (cos θ1cos θ2 – sin θ1sin θ2)
∴ u² = v1² + v2² + 2 v1v2 cos (θ1 + θ2)
using (3) in this equation, we get
2v1v2cos (θ1 + θ2) = 0
cos (θ1 + θ2) = 0
∴ θ1 + θ2 = \(\frac{\pi}{2}\)
i.e., the masses move at right angles after the collision.
![]()
Question 6.
An object of mass 0.4 kg moving with a velocity of 4ms-1 collides with another object of mass 0.6 kg moving in the same direction with a velocity of 2ms-1. If the collision is perfectly inelastic, what is the loss in K E due to impact?
Solution:
m1 = 0.4 kg, u1 = 4 ms-1 m2 = 0.6kg, u2 = 2 ms-1
∴ Total K E of system before collision
ki = \(\frac{1}{2}\) m1u1² + \(\frac{1}{2}\) m2u2²
\(\frac{1}{2}\) × 0.4 × 4² + \(\frac{1}{2}\) × 0.6 × 2²
= 3.2 + 1.2 = 4.4J
∴ As collision is perfectly inelastic, the common velocity after collision v is given by
v = \(\frac{m_{1} u_{1}+m_{2} u_{2}}{m_{1}+m_{2}}\) = \(\frac{0.4 \times 4+0.6 \times 2}{0.4+0.6}\)
= 2.8 ms-1
∴ Total K E of system after collision
kf = \(\frac{1}{2}\) (m1 + m2) v² = \(\frac{1}{2}\) (1) × (2.8)²
= 3.92 J.
∴ Loss in K E = Δ K E = Δ K = Ki – Kf
= 4.4 – 3.92 J
= 0.48 J.
1st PUC Physics Work, Energy and Power Additional Marks Questions and Answers
Question 1.
A force of 600 N displaces an object through 2 m. Find the work done if the force and displacement are
- Parallel
- At right angles.
Solution:
Work done is given by W = Fs cos θ
1. when F and s are parallel, θ = 0 and hence cos θ = 1
∴ W = Fs = 600 × 2 = 1200 J.
2. when F and s are at right angles,
θ = 90° and hence cos θ =0
∴ Work done, W = 0.
Question 2.
A sphere of radius 2mm and of density 7.5 × 103 kg m-3 falls from a height of 500m above the ground. Due to air resistance, its acceleration gradually decreases and becomes zero when it drops to half its original height. The drop then falls with a uniform terminal velocity. What is the work done by the gravitational force during the first and second half of its Journey?
Solution:
Even though the resultant force acting on the sphere is different during the first and second half of its journey, the force due to gravity remains constant throughout and is equal to the weight of the sphere. The amount of work done during the first half is given by,
W = mgh where m is the mass of the body.
But m = \(\frac{4}{3}\)πr3d and h = \(\frac{500}{2}\) = 250m
W = \(\frac{4 \pi}{3}\)(2 x 10-3)3 × 7.5 × 103 × 9.8 × 250
= 4\(\frac{4 \pi}{3}\) (2)3 × 7.5 × 9.8 × 250 × 10-6 J
= 615.4 × 10-3 = 0.615J
The work done remains the same during both the halves.
Question 3.
A pump is used to fill a tank 6m × 3m × 2m in half an hour. If the average height to which water to be lifted from the well is 110m, find the horsepower of the engine.
Solution:
Volume of the tank = 6 × 3 × 2 = 36m3
∴ mass of water to be lifted
= V × d = 36 × 103 kg
∴ Work done = mg × h
= 36 × 103 × 9.8 × 110
Power of the pump = \(\frac{W}{t}\)
= \(\frac{36 \times 9.8 \times 1.1 \times 10^{5}}{30 \times 60}\) = 0.216 × 105W
= \(\frac{0.216 \times 10^{5}}{746}\) = \(\frac{21600}{746}\) = 28.9 HP.
![]()
Question 4.
A circular well of radius 5m is filled with water to a height of 25m. It is emptied using a pump. If the efficiency of the pump is 60% and the initial level of water from the surface of the ground Is 10 m, calculate the time taken to empty it.
Solution:
If h1 and h2 are the heights of the initial and final levels of water in the well, then the average height through which water is lifted to empty it is,
h = \(\frac{h_{1}+h_{2}}{2}\) = \(\frac{10+35}{2}\) = 22.5 m
mass of water to be lifted
= volume × density = πr²Ld
Here, r = 5 m, L = 25m, d = 103 kgm-3
∴ total work to be done = mgh
= π × 5² × 25 × 103 × 9.8 × 25
= 1.73 × 107 ………………. (1)
Power of the pump used = 15 HP = 15 × 746 W
Total work done in lifting the water = 60% of the power of the pump.
If t is the time taken to empty it, the total amount of work done by the pump is
W = 15 × 746 × t.
Only 60% is used to lift the water.
∴ Amount of work done by the pump to lift water
W= \(\frac{60}{100}\) × 15 × 746 × t ………… (2)
Equating equation (1) and (2), we have,
1.73 × 107 = \(\frac{60}{100}\) × 15 × 746 × t
or t = \(\frac{1.73 \times 100 \times 10^{7}}{60 \times 15 \times 746}\)
= 2.5 × 103 S.
Question 5.
A lorry of mass 5 tons runs on a level track with a speed of 80km/hr. If the resistance due to air and friction is 80 N per ton, find the H.P. of the engine. Solution:
Total frictional force acting on the lorry is,
F = 5 × 80 = 400 N.
When a constant force is acting, then the power
P = x force × velocity
= 400 × \(\frac{80 \times 1000}{60 \times 60}\) W
= 8.89 × 103 W
= \(\frac{8.89 \times 10^{3}}{746}\) HP = 11.9 HP
Question 6.
An engine pulls a car of mass 1500 kg on a level road at a constant velocity of 5ms-1. If the frictional force is 500 N, what power does the engine generate? What extra power must the engine develop to maintain the same speed up a plane inclined to have gradient in 10?
Solution:
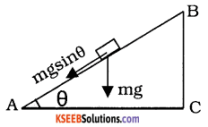
Since the car moves with a constant velocity, the power generated by the engine is just sufficient to overcome the frictional force.
P = F × V = 500 × 5
= 2500 W
= 2.5 kW
When the car moves over an inclined road, in addition to the friction, the engine must over come the component of the weight of the car along the inclined road. The component of the weight along the AB is, F = mg Sin θ
= 1500 × 9.8 × \(\frac{1}{10}\) (since Sin θ = \(\frac{1}{10}\))
∴ Extra power required = F × v
= 1500 × \(\frac{9.8 \times 5}{10}\)
= 7350 W = 7.35 kW
Question 7.
A gun of mass 5 kg fires a bullet of mass 10-2 kg with a speed of 5 x 10²ms-1. Find the kinetic energy of the bullet and the gun. Also, find the ratio of the distance moved by the gun due to recoil to that moved by the bullet.
Solution:
If m1 and m2 are the mass of the gun and the bullet and v1 and v2 are their corresponding velocities, then from the law of conservation of linear momentum,
Pi = Pf where Pi is the total initial momentum of bullet and the gun which is zero.
But P1 = m1v1 + m2 v2
m1v1 + m2 v2 = 0 or
v1 = \(\frac{m_{2} v_{2}}{m_{1}}\) = \(\frac{10^{-2} \times 5 \times 10^{2}}{5}\)
∴ Recoil velocity of the gun,
v1 = – 1 ms-1
∴ Kinetic energy of the bullet.
= \(\frac{1}{2}\) m2v2²
= \(\frac{1}{2}\) × 10-2 × (5 × 10²)²
= \(\frac{25 \times 10^{2}}{2}\) =12.5 × 10² J
Question 8.
A labourer weighing 70kgs climbs 11 step of a stair case each 0.21 m height in 1.4. Find the power in watt and the Horse Power (g = 9.8ms 2)
Solution:
Mass of labourer m = 70kg
Total height of stair case = 11 × 0.21
h = 2.31m
Time taken to climb = 1.4seconds, g = 9.8ms-2
∴ Work done, W = mgh
= 70 × 9.8 × 2.31
= 1585 J.
∴ Power P = \(\frac{W}{t}\) = \(\frac{1585}{1.4}\) = 1132 W
But, 1 HP =746 Watts
∴ Power in Horse power = 1.517 HP.
Question 9.
An engine is used to lift water from a well to a height of 40m to fill a tank 2m × 2m × 3m in 5 minutes. Find the power of the engine.
Solution:
Volume of the tank V = 2 × 2 × 3 = 12m3
∴ Mass of water to be lifted = v × d
= 12 × 103kg
∴ work done, W = mgh
= 12 × 103 × 9.8 × 40
∴ W = 4704 × 103J
∴ Power of the engine P = \(\frac{W}{t}\)
= \(\frac{4704 \times 10^{3}}{5 \times 60}\)
= 15.68 × 103W.
![]()
Question 10.
Find the height from which body of a mass 50kg should fall in order to have the K.E of a car of mass 200kg travelling at 10ms-1 Given g = 9.8ms-2
Solution:
Mass of a body, m1 = 50 kg
Mass of car m2 = 200kg
velocity of the car v = 10ms-1 g = 9.8ms-2
P.E of the body, P.E = mgh
= 50 × 9.8 × h
= 490h
K.E of the car K.E = \(\frac{1}{2}\) m2v²
= \(\frac{1}{2}\) × 200 × 10²
= 10,000J
But P.E of body = K.E of car
490h = 10,000
h = \(\frac{10,000}{490}\) = 20.41 m
Question 11.
A man fires 10 bullets, each of mass 20 × 10-3 Kg in every second with a gun of mass 10 Kg. If the velocity of each bullet is 300 ms-1, what force must be applied by the man to the gun to hold it in position? If the number of bullets fired per second doubles what will be a new force?
Solution:
No of bullets, N = 10
Mass of each bullet, M = 20 × 10-3kg
∴ Total mass of 10 bullets,
m = N × M
= 10 × 20 × 10-3
= 200 × 10-3kg
Velocity of each bullet = 300ms-1
From, the equation, F = ma
= \(m\left(\frac{v-u}{t}\right)\)
= 200 × \(10^{-3}\left(\frac{300-0}{1}\right)\)
= 60 N
∴ Force required by the man to the gun to hold it in position is 60N.
If the number of bullets fired per sec doubles, then force required also doubles.
Question 12.
A bullet of mass 20gm strikes a wooden plank with a velocity of 60ms-1 and emerges out in 0.01 seconds with a velocity of 30ms-1. Calculate
(i) the work done by the bullet and
(ii) the thickness of the plank.
Solution:
Given m = 20 × 10-3kg
u = 60ms-1 & v = 30 ms-1
work done = decrease in kinetic energy
= \(\frac{1}{2}\) m (u² – v²)
= \(\frac{1}{2}\) × 0.02 (60² – 30²)
= 27J
From, v = u + at
30 = 60 + a (0.01)
a = \(\frac{-30}{0.01}\) = – 3000 ms-2
Retarding force, F = ma
= 0.02 × 3000 = 60N
work done, W = F × S
27 = 60 × S
∴ Thickness of the plank, S = \(\frac{27}{60}\)
= 0.45m.
Question 13.
A body of mass 0.1 kg falling freely under gravity takes 10second to reach the ground. Calculate kinetic energy & potential energy of the body, when the body has travelled for 6 seconds.
Solution:
Given: m = 0.1 kgm, u = 0,
t = 6 sec, a = g
∴ From v = u + at
v = 0 + 9.8 × 6
v = 58.8 ms-1
∴ kinetic energy of the body, when the body has travelled for 6 seconds, is
K.E = \(\frac{1}{2}\) mv²
= \(\frac{1}{2}\) × 0.1 × (58.8)²
K.E = 172.9 J
To Find Potential Energy (PE):
Distance travelled by the body in 10 sec, is
S10 = ut + \(\frac{1}{2}\) gt²
= 0 + \(\frac{1}{2}\) × 9.8 × 10²
S10 = 490m
Distance travelled by the body in 6 sec is
S6 = ut + \(\frac{1}{2}\)gt²
= 0 +\(\frac{1}{2}\) × 9.8 × 6²
S6 = 176 .4m
∴ h = S10 – S6 = 490 – 176 .4 = 313.6m
∴ P.E = mgh
= 0.1 × 9.8 × 313.6
= 307.3 J.