Students can Download 2nd PUC Basic Maths Model Question Paper 1 with Answers, Karnataka 2nd PUC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Model Question Paper 1 with Answers
Time: 3.15 hours
Max. Marks: 100
Instructions
- The question paper has 5 parts A, B, C, D, and E. Answer all the parts.
- Part – A carries 10 marks, Part – B carries 20 marks, Part – C carries, Part – D carries 30 marks and Part – E carries 10 marks.
- Write the question number properly as indicated in the question paper.
Part – A
I. Answer all the questions: (10 × 1 = 10)
Question 1.
Define Diagonal Matrix
Answer:
In a square matrix, except the principal diagonal elements all other elements are zeros is called diagonal matrix.
\(\left[ \begin{matrix} 2 & 0 \\ 0 & 3 \end{matrix} \right]\) \(\left[ \begin{matrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 4 \end{matrix} \right]\)
Question 2.
In how many ways can 9 soldiers stand in a queue.
Answer:
9 soldiers can stand in a queue in 9! ways
Question 3.
Symbolise the following proposition: 3x = 9 and x < 7
Answer:
(i) Let p:3x = 9, q = x < 7
Given in symbols is p ∧ q
![]()
Question 4.
Find the subtriplicate ratio of 125 : 64.
Answer:
Subtriplicate ratio of 125 : 64
= 3√125 : 3√64 = 5 : 4.
Question 5.
Define Banker’s Discount.
Answer:
Banker’s Discount is the Simple interest calculated by the banker on the face value of the bill i.e., BD = Ftr
Question 6.
If sin A = \(\frac { 1 }{ 2 }\) find sin 2A
Answer:
Given sin A = \(\frac { 1 }{ 2 }\) ⇒ cos A = \(\frac{\sqrt{3}}{2}\) sin2A
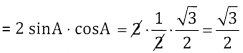
Question 7.
Find the equation of the circle with centre ‘C and radius ‘r’ of the following: c{-3, 2) and r = 5 units
Answer:
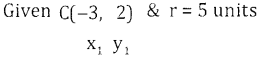
Equation of the circle is(x – x1)2 + (y – y1)2 = r2
(x-(-3))2 + (y – 2)2 = 52
(x + 3)2 + (y – 2)2 = 52
x2 + y2 + 6x – 4y – 12 = 0.
Question 8.
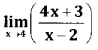
Answer:
\(=\frac{4.4+3}{4-2}=\frac{16+3}{2}=\frac{19}{2}\)
Question 9.
5ex – logx – 3\(\sqrt{\mathbf{x}}\)
Answer:
Let y = 5ex – log x – 3\(\sqrt{x}\)
\(\frac{d y}{d x}=5 e^{x}-\frac{1}{x}-3 \frac{1}{2 \sqrt{x}}\)
![]()
Question 10.
Integrate the following x2 – \(\frac { 6 }{ x }\) + 5ex
Answer:
\(\int x^{2}-\frac{6}{x}+5 e^{x} d x=\frac{x^{3}}{3}-6 \log x+5 e^{x}+C\)
Part – B
II. Answer any ten questions: (10 × 2 = 20)
Question 11.
Find x and y given that \(\left[ \begin{matrix} -9 \\ 2 \end{matrix} \right] -\left[ \begin{matrix} 5 \\ -1 \end{matrix} \right] =\left[ \begin{matrix} x \\ y \end{matrix} \right] \)
Answer:
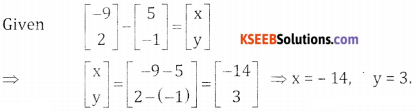
Question 12.
If nC8 = nC12 find nC5
Answer:
Given nC8 = nC12
⇒ n = 8 + 12 = 20
nC5 = 20C5 = 15,504.
Question 13.
What are independent events? Give one example.
Answer:
(a) If two events cannot occur simultaneously in a random experiment then they are called mutually exclusive events
(b) Events are said to be independent, if the occurrence of one does not depend upon the occurrence of the other
(c) In a random experiment, let S be the sample space & let E be an event then E C S, So ‘E’ is also an event called the complementary of E.
Question 14.
If p, q and r are propositions with truth values F, T and F respectively, then find the truth value of the following compound proposition: (p ∧ q) v ~ r
Answer:
(p ∧ q) ∨ ~ r
(F ∧ T) ∨ ~ r
F ∨ T
= T
![]()
Question 15.
Find the ratio between two numbers such that their sum is 40 and their difference is 8.
Answer:
Let the two numbers be x & y
Given x + y = 40 ……. (1)
& x – y = 8 … (2)
Solving we get
Adding 2x = 48 ⇒ x = 24 & y = 40 – 24 = 16
∴ Ratio of the numbers is 24 : 16 ⇒ 3:2.
Question 16.
Find the BD on ? 1015, payable after 3 months at 6% p.a.
Answer:
Given
F = 1015,
F=1015, t = \(\frac{3}{12}\) year, r = \(\frac{6}{100}\) = 0.06, BD = ?
BD = Ftr = 1015 x \(\frac{3}{12}\) × 0.06 = 15.22
Question 17.
If sin A = \(\frac { 3 }{ 5 }\), cos B = \(\frac { 4 }{ 5 }\) find sin(A + B) and cos(A – B). Where A and B are acute angles.
Answer:
Given sin A = \(\frac { 3 }{ 5 }\) , cos B = \(\frac { 4 }{ 5 }\)
⇒ cos A = \(\frac { 4 }{ 5 }\) & sin B = \(\frac { 3 }{ 5 }\) ∵ sin2A + cos2A = 1
(i) sin(A + B) = sinA cosB + cosA sinB = \(\frac{3}{5} \cdot \frac{4}{5}+\frac{4}{5} \cdot \frac{3}{5}=\frac{24}{25}\)
(ii) cos(A – B) = COSA COSB + sinA sinB = \(\frac{4}{5} \cdot \frac{4}{5}+\frac{3}{5} \frac{3}{5}=\frac{16}{25}+\frac{9}{25}=\frac{25}{25}=1\)
Question 18.
\(\cos \left(\frac{\pi}{4}-A\right)-\sin \left(\frac{\pi}{4}+A\right)=0\)
Answer:
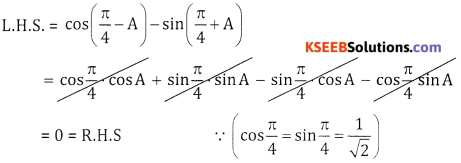
Question 19.
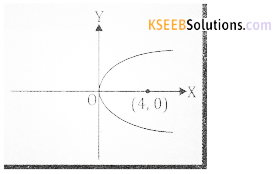
Find the equation of the parabola given that its. Vertex is (0,0) and focus is (4, 0)
Answer:
(a) Given V = (0,0) and Focus, S = (4,0)
It is a right handed parabola with
a = 4 and standard form is
y2 = 4ax
Put a = 4, then
y2 = 16x.
![]()
Question 20.
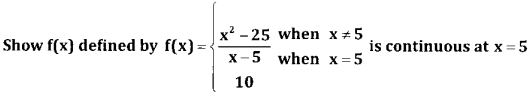
Answer:
Also f(x) at x = 5 is 10; i.e, f(5) = 10
![]()
∴ the function f(x) is continuous at x = 5
Question 21.
Differentiate e2x w.r.t. x from first principles.
Answer:

Question 22.
The displacement ‘s’ of a particle at time ‘t’ is given by S = 4t3 – 6t2 + t – 7. Find the velocity and acceleration. when t = 2 sec.
Answer:
Given S = 4t3 – 6t + t – 7
Velocity = v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 12t2 -12t + 1
At t = 2secs, v = 12(2)2 – 12(2) + 1 = 48 – 24 + 1 = 25 units/sec.
At t = 2 sec, acceleration = 24.2 – 12 = 48 – 12 = 36 units/sec2.
Question 23.
sec x(sec x – tan x)
Answer:
∫sec x (sec x – tan x)dx = ∫sec2x – sec x .tan x. dx
= tan x – sec x + c
Question 24.
Jsin2x dx
Answer:
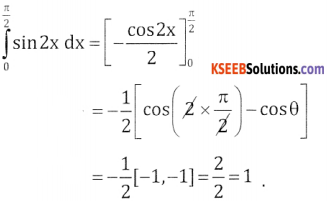
![]()
Part – C
III. Answer any Ten Questions: (10 × 3 = 30)
Question 25.
Find A and B if 2A + B = \(\left[ \begin{matrix} 1 & -1 \\ 0 & 1 \end{matrix} \right]\) and A – 3B = \(\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} \right]\)
Answer:

Question 26.
Show that, if any row of column of a determinant contains sum of two terms then it can be expressed as sum of two determinants
Answer:
If any row of a column of a determinant contains sum of two terms then it can be expressed as sum of two determinants
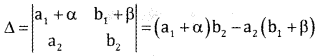
= a1b2 + αb2 -a2 – a2b1 – a2β
= (a1b2 – a2b1) + αb2 – βa2
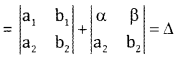
Question 27.
Find the number of permutations of the letters of the word MISSISSIPPI. In how many of these
(a) the 4s’s are together
(b) the 4s’s are not together
(c) begin with MISS
Answer:
Total letters = 11, I = 4, S = 4, P = 2.
∴ The total number of permutations 7
4s’s are together can be taken as 1 unit i.e.

∴ The number of permutations = \(\frac{8 !}{4 ! \times 2 !}\) (b)
4s’s are not together = Total number of ways – 4s’s are together = \(\frac{11 !}{4 ! \times 4 ! \times 2 !}-\frac{8 !}{4 ! \times 2 !}\) (c)
Begin with MISS: The remaining 7 letters can be arranged in \(\frac{7 !}{3 ! \times(2 !)^{2}}\) (d)
Begin with SIP: The remaining 8 letters (I = 3, S = 3) can be arranged in \(\frac{8 !}{(3 !)^{2}}\)
![]()
Question 28.
A box contains 4 defective and 6 non defective bulbs. Find the probability that atleast 3 bulbs are defective when 4 bulbs are selected at random.
Answer:
A box contains 4 defective and 6 non def when 4 bulbs are selected at random.
Answer:
n(S) = (6 + 4)C4 = 10 \(c_{4}-\frac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1}\) = 210
Let A: at least 3 are defective
Here 4 defective 6non defective

Question 29.
Two taps fill a cistern separately in 20 minutes and 40 minutes respectively and a drain pipe can drain off 30 litres per minute. If all the three pipes are opened, the cistern fills in 72 minutes what is the capacity of the cistern?
Answer:
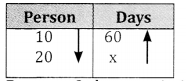
Persons & days are in inverse proportion
∴ 10:20 = x : 60
X= \(\frac{60 \times 10}{20}\) = 30days 20
Question 30.
Refrigerator is marked for sales for ?17,000 which include sales tax at 10% Calculate the sales tax in
Answer:
Given S.P = ₹ 17,000, Sales Tax = 10% Let
C.P = x₹
W.K.T selling price = CP + Sales Tax
17,000 = x + 10% of
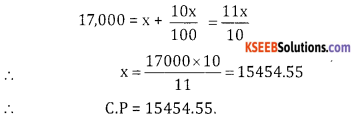
Question 31.
The difference between banker’s discount and true discount on a bill due after 6 months at 4% interest p.a. is t20. Find the true discount, banker’s discount and face value of the bill.
Answer:
Given
BG = ₹ 20, r = 4% = 0.04, t = 6 Months = \(\frac{6}{12}=\frac{1}{2}\)
TD = ?, BD = ?, F = ?
W.K.T. = BG = TD. tr
20 = TD \(\frac{1}{2}\) x 0.04
40 = 0.04 TD ⇒ TD = \(\frac{40}{0.04}\) = ₹ 1000
BD = BG + TD; = 20 + 1000 = 1020
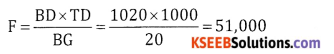
Question 32.
A man invests equal sums of money in 4%, 5% and 6% stock, each stock being at par. If the total income of the man is ₹ 3,600. Find his total investment.
Answer:
Let the amount invested be x

![]()
Question 34.
Find \(\frac{\mathrm{d} y}{\mathrm{d} x}\) if x = a sec θ, y = b tan θ dx
Answer:
Given a = secθ, y = b tan θ
Differentiate both w.r.t. θ we get

Question 35.
The radius of sphere is increasing at the rate of 0.5mt/sec. Find the rate of increase of its surface area and volume after 3 sec.
Answer:
Given \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 0.5 , t = 3 sec, \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = ? \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = ?
surface area = s = 4πr2
\(\frac{d s}{d t}\) = 4π . 2r . \(\frac{d r}{d t}\)
= 4π × 2 × 1.5 × 0.5
= 6π m2/sec
dr = 0.5 × dt
⇒ r = 0.5 t
= 0.5 × 3
= 1.5
Question 36.
The sum of two natural numbers is 48. Find the numbers when their product is maximum.
Answer:
Let the two numbers be x & y.
Given x + y = 48 & product: = xy where y 48 – x.
Let p = xy = x (48 – x) = 48x – x2.
\(\frac{d p}{d x}\) = 48 – 2x
\(\frac{d p}{d x}\) = 0 ⇒ 48 – 2x = 0 x = 24
\(\frac{\mathrm{d}^{2} \mathrm{p}}{\mathrm{d} \mathrm{x}^{2}}\) = -2 < 0 ⇒ product is maximum
x = 24 ⇒ y = 48 – 24 = 24
⇒ the two numbers are 24, 24.
Question 37.
Integrate the following \(\sqrt{1+\sin 2 x}\)
Answer:
\(\int \sqrt{1+\sin 2 x} d x=\int \sqrt{(\cos x+\sin x)^{2}}=\int(\cos x+\sin x) d x\)
= sinx – cosx + c
Question 38.
Answer:
Let
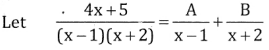
4x + 5 = A(x + 2) + B(x – 1)
put x = 1, 4 + 5 = A(1 + 2) + B(0)
9 = 3A ⇒ A = 3
put x = -2 -8 + 5 = A(0) + B(-2 -1)
-3 = -3B ⇒ B = 1
∴ \(\int \frac{4 x+5}{(x-1)(x+2)} d x=\int\left(\frac{3}{x-1}+\frac{1}{x+2}\right) d x\) =3log(x – 1) + log(x + 2) +c
![]()
Part – D
IV. Answer any six questions: (6 × 5 = 30)
Question 39.
\((\sqrt{3}+1)^{5}-(\sqrt{3}-1)^{5}\)
Answer:

Question 40.
\(\frac{x^{2}-10 x+13}{(x+1)\left(x^{2}-5 x+6\right)}\)
Answer:
Let
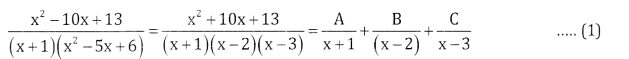
x2 – 10x + 13 = A(x-2)(x – 3) + B(x +1) (x – 3) + C(x + 1) (x – 2)
Put x=-1, 1 + 10 + 13 = A (-3) (-4) + 0 + 0
24 = 12A ⇒ A = \(\frac{24}{12}\)=2
Put x = 2, 4 – 20 + 13 A(0) + B(3) (-1) + C(0)
-3 = -3B ⇒ B = 1
Put x = 3, 9 – 30 + 13 = A(0) + B(0) + C(4) (1)
-8 = 47 ⇒ C= -2
![]()
Question 41.
Define Tautology and show that (p → q) + (~ q → – p) is a Tautology.
Answer:
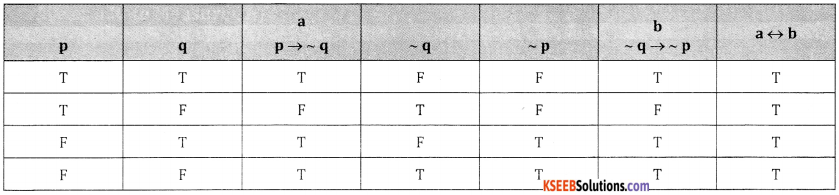
Question 42.
Divide ₹ 1800 is three parts such that three times of the first, five times of the second and six times the third are equal.
Answer:
Let the 3 parts be x, y and z
Given 3x = 5y = 62
Let 3x = 6z and 5y = =\(\frac{6}{5} \)z
x = 2z, y = 2
∴ x : y : z = 2z : \(\frac{6}{5}\)z : z= 10:6:5
Sum of the ratios = 10 + 6 + 5 = 21
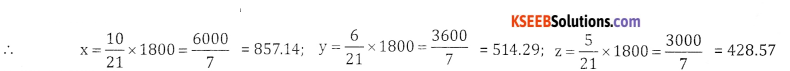
![]()
Question 43.
The time required to produce the first unit of a product is 1000 hours. If the manufacturers experiences 80% learning effect calculate the average time per unit & the time taken to produce altogether 8 units. Also find the total labour charges for the production of 8 units at the rate of ₹ 12.50 per hour.
Answer:
I. Table method
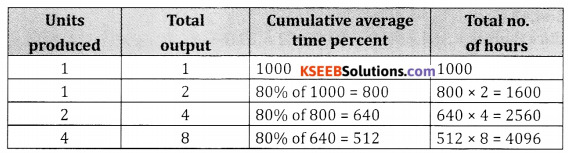
Total time to produce 8 units = 4096 hrs.
Given labour charges for 1 hour = ₹ 12.50
∴Labour charges for 4096 hours = 4096 x 12.50 = ₹ 51,200
II. Formula Method:
Given a = 1000, x = 8 units

y = axb
log y = loga + b log x = log1000 + (-0.3219) log 8
= 3.000 – 0.3219 x 0.9031 = 3.000 – 0.2907
log y = 2.7093
y = AL (2.7093) = 512 hrs. per unit
∴ Total time for 8 units = 512 x 8 = 4,096 hrs.
Labour charges per hour = ₹ 12.50.
∴ Labour charges for 4,096 hrs. = 4,096 x 12.50 = 51,200
Question 44.
Solve the following linear programming problems using graphical method
Maximise z = 5x + 3y subject to
3x + 5y ≤ 15
5x + 2y ≤ 10
x ≥ 0, y ≥ 0
Answer:
Consider 3x + 5y = 15
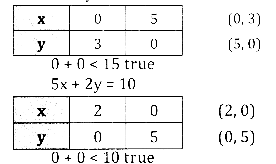
Plot the lines on the graph.
O ABC is the solution region.

X is maximum at B( \(\frac{20}{19}, \frac{45}{19}\) )
zmax = \(\frac{235}{19}\) = 12.37
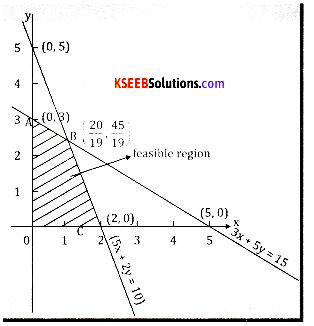
![]()
Question 45.
cos10°.cos30°. cos50°.cos 70° = \(\frac { 3 }{ 16 }\)
Answer:

Question 46.
Find the equation of the circle.Passing through the points (5,1), (3,4) and has its centre on the x – axis.
Answer:
Let the required equation of the circle is x2 + y2 + 2gx + 2fy + c = 0
It passes through (5, 1) & (3, 4)
(5, 1) (5)2 + (1)2 + 2g(5) + 2f (1) +C = 0
10g + 2f + C + 26 = 0 …..(1)
(3,4) 32 + 42 + 2g (3) + 2f (4) +c= 0
68 + 8f + C + 25 = 0 …..(2)
& the centre (- g, – f) lies on x-axis ⇒ f = 0 ….(3)
Solving 1 & 2 we get
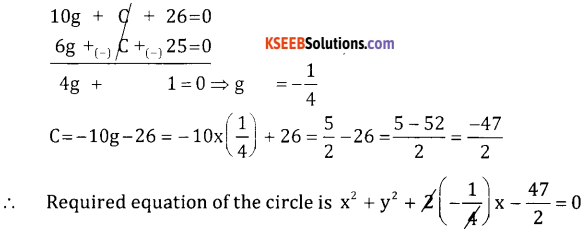
⇒ 2x2 + 2y2 – x – 47 = 0.
Question 47.
xlogx + (log x)x
Answer:
Let y = xlogx + (log x)x
y = u + v
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) …(1)
Where u = x and v = (log x)x
Taking logm both sides
log u = log x . log x log v = x log (log x)
Differentiate both w.r.t. x

![]()
Question 48.
Find the area bounded by the parabola y2 = 4ax and its latus rectum.
Answer:

Part – E
V. Answer any one questions. (1 × 10 = 10)
Question 49.
(a) Solve by Matrix Method x + y+ z = 5, 2x + y – z = 2, 2x – y + z = 2.
Answer:

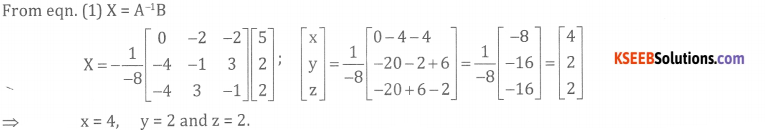
OR
![]()
Question 49.
(a) Show that the following points are concylic.
(0,0), (1,1), (5,-5), (6,-4)
Answer:
First find the equation of the circle passing through the points (0,0) (1, 1) (5,-5) (6,-4)
(0,0) ⇒ C = 0 …. (1)
(1, 1) ⇒ 2g + 2f + 2 = 0 …. (2)
(5,-5) ⇒ 10g -10f + 50 + c = 0 …. (3)
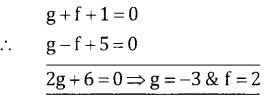
∴ The equation of the circle is x2 + y2 – 6x + 4y = 0
Substituting the fourth point (6,-4) we get
36 + 16 – 36 – 16 = 0 ⇒ 0 = 0
∴ The points are concyclic.
Question 49.
(b) Smaran being a manufacturer produces nuts and bolts for industrial machinery. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts while it takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of ? 2.50 per package on nuts and ? 1 per package on bolts. Form a linear programming problem to maximize his profit, if he operates each machine for at most 12 hours a day.
Answer:

Let the number of units of nuts x & bolts be y it takes 1 hour on machine A for a nut and 3 hours on machine 13 for a nut maximum time available for machine A is 12 hours.
∴ x + 3y ≤ 12
3x + y ≤ 12
Negative units cannot be produced: x, y ≥ 0 our objective is to maximum profit the LPP is Maximize = 2.5 x + y subject to
x + 3y ≤ 12
3x + y ≤ 12
and x ≥ 0, y ≥ 0
Question 49.
(b) Find the average cost and Marginal cost if the total cost function of an article is given by c = 5x + 2x + 3(x = quantity).
Answer:
Given T.C = C(x) = 5x2 + 2x + 3; M.C = \(\frac{d}{d x}\) (T.C) = 10x + 2
A.C = \(\frac{C(x)}{x}=\frac{T \cdot C}{x}=\frac{5 x^{2}+2 x+3}{x}\) = 5x + 2 + \(\frac{3}{x}\)
Question 50.
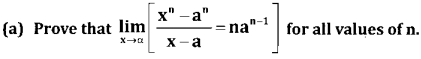
Answer:
Case 1: Let n be a positive integer.
xn – an = (x – a)n(xn-1 + xn-2 . a + xn-3 . a2 + …. + an-1)

= an-1 + an-2.a2 + ……. + an-1 = an-1 + an-1 + an-1 + ……. + an-1
= n . an-1
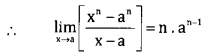
![]()
Case 2: Let n be a negative integer
Put n = -m, m > 0

Case 3: Let n = p/q where p and q are integers and q ≠ 0

![]()
(b). Use binomial theorem to evaluate upto 4 decmials place (102)6
Answer:
(102)6 = (100 + 2)6
= (100)6 + 6C1(1 0O)5. 2 + 6C2(100)4.22 + 6C3(100)3.23 + 6C4(100)2 24 + 6C5.100.25 + 6C626
= 1000000000000 + 120000000000 + 6000000000 + 160000000 + 2400000 + 19200 + 64
= 1,126,162,419,264