Students can Download Basic Maths Exercise 15.2 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 15 Circles Ex 15.2
Part – A
2nd PUC Basic Maths Circles Ex 15.2 One Mark Questions and Answers
Question 1.
Find the centre and the radius of the circle.
(a) x2 + y2 – 4x – y – 5 = 0
(b) 3x2 + 3y2 – 6x – 12y – 2 = 0
(c) (x – 2) (x – 4) + (y – 1) (y – 3) = 0
(d) x2 + y2 – 2x cosα – 2y sinα = 1
Answer:
(a) x2 + y2 – 4x – y – 5 = 0 Comparing with
x2 + y2 + 2gx + 2fy + C = 0 We get
2g = – 4, 2f = – 1 ⇒ g = -2, f = \(-\frac{1}{2}\)
∴ C=(-8,-1) = (2, \(\frac{1}{2}\))
\(r=\sqrt{g^{2}+f^{2}-C} ; \quad r=\sqrt{(-2)^{2}+\left(-\frac{1}{2}\right)^{2}-(-5)}=\sqrt{4+\frac{1}{4}+5}=\sqrt{\frac{16+1+20}{4}}=\frac{\sqrt{37}}{2} \text { units }\)
(b) Given 3x2 + 3y2 – 6x – 12y – 2 = 0, divide by 3
x2 + y2 – 2x – 4y – \(\frac{2}{3}\) = 0
Here g = -1, f = -2, & c = \(-\frac{2}{3}\)
∴Centre = (-g, -f) = (1, 2) & r =\(\sqrt{g^{2}+f^{2}-C}\)
\(=\sqrt{(-1)^{2}+(-2)^{2}-\left(-\frac{2}{3}\right)}\)
r = \(\sqrt{1-4-\frac{2}{3}}=\sqrt{\frac{17}{3}}\) units.
![]()
(c) Given (x – 2) (x – 4) + (y – 1) (y – 3) = 0
⇒ x2 – 6x + 8 + y2 – 4y + 3 = 0
⇒ x2 + y2 – 6x – 4y + 11 = 0
Here g = -3, f= -2, C = 11 & ∴ Centre = (3,2).
And r = \(\sqrt{9+4-11}=\sqrt{2}\) units
(d) Given x2 + y2 – 2x cos α – 2y sin α – 1 = 0
g = – cosα, f = – sinα, c = -1
∴ Centre = (cosα, sinα) & r = \(\sqrt{\cos ^{2} \alpha+\sin ^{2} \alpha+1}=\sqrt{1+1}=\sqrt{2}\)
Question 2.
If the radius of the circle x2 + y2 + 4x – 2y- k = 0 is 4 units find k.
Answer:
Given x2 + y2 + 4x – 2y – k = 0 & r = 4 units, K = ?
Here g = 2, f = -1 and C = – k
∴ Centre = (-2, 1) & r = \(\sqrt{g^{2}+f^{2}-c}\)
4 = \(\sqrt{(2)^{2}+(-1)^{2}-(-k)}\) ⇒ 4 = \(\sqrt{4+1+k}\) S.B.S
16 = 5 + k ⇒ k = 16 – 5 = 11
Question 3.
Find the other end of the diameter, if one of the diameter of the circle.
(a) x2 + y2 = 25 is (5,0)
(b) x2 + y2 + 4x – 6y – 12 = 0 is (-5, -1)
(c) x2 + y2 – 6x + 2y = 31 is (7,4)
Answer:
(a) Given x2 + y2 = 25, A = (5,0) Let (x2 y2) = ?
Here C =(0,0) & We know that centre is the midpoint of the diameter.
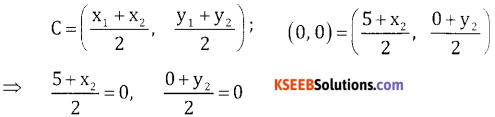
⇒ 5 + x2 = 0 0 + y2 = 0
⇒ x2 = -5 y2 = 0
∴ The other end of the diameter B = (-5,0).
(b) Given x2 + y2 + 4x – 6y – 12 = 0,
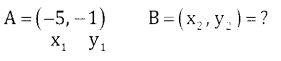
Here C = (-2,3)
∴ By mid point formula we have
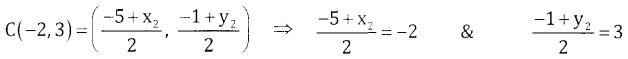
⇒ x2 = -4 + 5 = 1 & y2 = 6 + 1 = 7
∴ The other end of the diameter B = (1,7)
![]()
(c) Given x2 + y2 – 6x + 2y – 31 = 0, A = (7,4), B = (x2, y2) = ?
Here C = (3,-1)
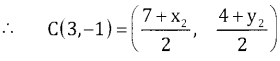
⇒ 7 + x2 = 6 & 4 + y2 = -2
⇒ x2 = -1 y2 = -6
∴ Other end of the diameter B = (-1,-6).
Question 4.
If(a, b) and (-5, 1) are the two end points of diameter of the circle x2 + y2 + 4x – 4y = 2. Find the value of a and b.
Answer:
Given (x1 y1) = (a, b) (x2, y2) = (-5, 1) & Center of the given circle = (-2,2).
Equation of the circle when ends of diameter is given is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0.
(x – a) (x + 5) + (y – b) (y – 1) = 0.
⇒ x2 – 5a – ax + 5x + y2 – by – y + b = 0.
x2 + y2 + x (5 – a) – y(b + 1) + (b – 5a) = 0 comparing.
This by given circle x2 + y3 + 4x – 4y – 2 = 0 we get
5 – a = 4, b + 1 = 4
⇒ 5 – 4 = a, b = 4 – 1
∴ a = 1 & b = 3.
Question 5.
If x2 + y2 – 4x – 8y + k = 0 represents a point circle find k
Answer:
Given x2 + y2 – 4x – 8y + k = 0 is a point circle
⇒ r = 0, g = -2, f = -4 & c = k
and \(\sqrt{g^{2}+f^{2}-C}=r\)
\(\sqrt{4+16-\mathrm{k}}=0 \quad=\sqrt{20-\mathrm{k}=0}\) ⇒ k = 20 S.B.S
![]()
Question 6.
If x2 + y2 + ax + 2y + 5 = 0 represent a point circle find a
Answer:
Given x2 + y2 + ax + 2y + 5 = 0 is a point circle.
⇒ r = 0, g = \(+\frac{a}{2}\) f = 1, C = 5
and \(\sqrt{g^{2}+f^{2}-C}=r=0\)
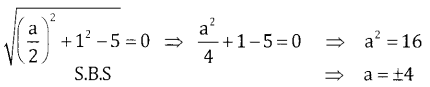
Question 7.
If x2 + y2 + ax + by = 3 represents a circle with centre at (1, -3), find a and b.
Answer:
Given x2 + y2 + ax + by – 3 = 0 & center = (1, -3), a = ?, b = ?
Here \(\frac { a }{ 2 }\) = 1 & \(\frac { b }{ 2 }\) = -3
⇒ a = 2 & b = – 6.
Question 8.
Find the unit circle concentric with the circle x2 + y2 – 8x + 4y = 8.
Answer:
Here unit circle ⇒ r= 1
& Center of concentric circle x2 + y2 – 8x + 4y – 8 = 0
C = (4, -2) & r =\(\sqrt{(-4)^{2}+(2)^{2}-(C)}=\sqrt{16+4-C}=1\)
⇒ 20 – C = 19
⇒ C = 19
∴ The Equation of the circle is x2 + y2 – 8x + 4y + 19 = 0.
![]()
Part-B
2nd PUC Basic Maths Circles Ex 15.2 Two Marks Question and Answers
Question 1.
Find the equation of the circle whose centre is same as the centre of the circle x2 + y2 + 6x + 2y + 1 = 0, and passing through the point (-2, -3).
Answer:
Given x2 + y2 + 6x + 2y + 1 = 0, P = (-2,-3)
Centre = C(-3,-1),
Let the equations of the required circle is x2 + y2 + 6x + 2y + C = 0
r = CP = \(\sqrt{(-2+3)^{2}+(-3+1)^{2}}=\sqrt{1^{2}+0}=1\)
∴ r = \(\sqrt{g^{2}+f^{2}-c}\)
l = \(\sqrt{9+1-c}\) ⇒ 1 = 10 -c ⇒ c = 9
∴ The required equation of the circle is
x2 + y2 + 6x + 2y + 9 = 0.
Question 2.
Find the equation of the circle whose centre is same as the centre of the circle x2 + y2 – 6x + 4y + 9 = 0 and Passsing through the point (-2,3)
Answer:
Given x2 + y2 – 6x + 4y + 9 = 0, & P = (-2,3)
Centre = c(3,-2), P = (-2,3)
r = cp = \(\sqrt{(-2-3)^{2}+(3-(-2))^{2}}=\sqrt{25+25}=\sqrt{50}\)
Let equation of the required circle is
x2 + y2 – 6x + 4y + c = 0
r = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{9+4}\) ∴ \(\sqrt{50}=\sqrt{13-c}\) ⇒ 50 = 13 – c ⇒ c = – 37
∴ The required circle is x2 + y2 – 6x + 4y – 37 = 0.
Question 3.
Find the equation of the circle whose centre is (-2, 3) and passing through the centre of the circle x2 + y2 – 6x + 4y+9=0.
Answer:
Given c= (-2,3) & given x2 + y2 – 6x + 4y + 9 = 0. P = (3,-2)
r = cp = \(\sqrt{(3+2)^{2}+(-2-3)^{2}}=\sqrt{25+25}=\sqrt{50}\)
Also r = \(\sqrt{g^{2}+f^{2}-c}\)
\(\sqrt{50}=\sqrt{4+9-c}\) ⇒ 50 = 13 – C ⇒ c = -37
∴ Required circle with c = (-2-3) & r = \(\sqrt{50}\) is (x + 2)2 + (y – 3)2 = \((\sqrt{50})^{2}\)
x2 + y2 + 4x – 6y – 37 = 0.
![]()
Question 4.
Find the equation of the circle passing through the centre of the circle x2 + y2 – 2x – 4y – 20 = 0 and centre at (4, -2).
Answer:
Given x2 + y2 – 2x – 4y – 20 = 0 & c = (4, -2)
∴ P= (1, 2)
r = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{16+4-(-c)}=\sqrt{20-c}\)
But r = CP = \(\sqrt{(4-1)^{2}+(-2-2)^{2}}=\sqrt{3^{2}+(-4)^{2}}=\sqrt{25}=5\)
∴ r = \(\sqrt{20-c}\) ⇒ 5 = \(\sqrt{20-c}\)
⇒ 25 = 20 – c ⇒ c = -5
∴ The required equation of the circle is x2 + y2 – 8x + 4y – 5 = 0.
Question 5.
Find the equation of the circle two of whose diameters are x + y = 3 and 2x + y = 2 and passing through the centre of the circle x2 + y2 – 4x + 2y – 1 = 0.
Answer:
Given x2 + y2 – 4x + 2y – 1 = 0
P = (2,-1)
& centre of the circle is point of intersection of diameters
x + y = 3 – (1) & 2x + y = 2 – (2)
eqn. (2) – eqn. (1) gives x = -1 & y = 3 – x = (3 – C – 1) = 4
∴ centre = c(-1,4)
r = CP = \(\sqrt{(-1-2)^{2}-\left(4-(-1)^{2}\right.}-\sqrt{(-3)^{2}+5^{2}}=\sqrt{9+25}=\sqrt{34}\)
∴ the eqn. of the circle with c = (-1,4) & r = \(\sqrt{34}\) is
(x + 1)2 + (y – 4)2 = \((\sqrt{34})^{2}\)
x2 + 1 + 2x + y2 + 16 – 8y = 34
x2 + y2 + 2x – 8y – 17 = 0.
Question 6.
Find the equation of the circle concentric with the centre of circle x2 + y2 – 2x + 2y – 1 = 0 and having double its area.
Answer:
Given x2 + y2 – 2x + 2y – 1 = 0
c = (1, -1) & rı = \(\sqrt{1+1-(-1)}=\sqrt{3}\)
Given A2, = 2A,
![]()
r22 =2 . \((\sqrt{3})^{2}\) = 2.3 = 6 ⇒ r2 = \(\sqrt{6}\)
Equation of the required circle with c = (1,-1) & r = is (x – 1)2 + (y + 1)2 = \((\sqrt{6})^{2}\).
x2 + 1 – 2x + y2 + 1 + 2y = 6 ⇒ x2 + y2 – 2x + 2y – 4 = 0.
![]()
Question 7.
Find the equation of the circle concentric with the centre of the circle 3x2 + 3y2 – 6x + 9y – 2 = 0 and \(\frac { 2 }{ 3 }\) having of its area.
Answer:
Given 3x2 + 3y2 – 6x + 9y – 2 = 0, divide by 3
x2 + y2 – 2x + 3y – \(\frac { 2 }{ 3 }\) =0
centre = (1, \(\frac{-3}{2}\)) & r = \(\sqrt{1+\frac{9}{4}-\frac{2}{3}}=\sqrt{\frac{47}{12}}\)
Also given A2 = \(\frac{2}{3}\) A1
πr22 = \(\frac{2}{3}\) . πr22 ⇒ r22 = \(\frac{2}{3} \times \frac{47}{12}=\frac{47}{18}\)
∴ Required circle with centre \(\left(1,-\frac{3}{2}\right), r_{2}-\sqrt{\frac{47}{18}} \text { is }(x-1)^{2}+\left(y+\frac{3}{2}\right)^{2}=(\sqrt{\frac{47}{18}})^{2}\)
x2 + 1 – 2x + y2 + 3y + \(\frac{9}{4}=\frac{47}{18}\)
x2 + y2 – 2x + 3y + \(\frac{23}{36}\) = 0 __________ × 36
36x2 + 36y2 – 72x + 108y + 23 = 0.
Question 8.
Find the equation of the diameter of the circle x2 + y2 + 6x – 2y = 6 which when produced passes through the point (1, -2).
Answer:
Given x2 + y2 + 6x – 2y – 6 = 0 & P (1, -2) centre = (-3, 1)
Slope of the diameter = m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{1-(-2)}{-3-1}=\frac{3}{-4}\)
∴ Equation of the diameter with (1, -2) & m = \(\frac{-3}{4}\)
y – y1 = m(x – x1)
y + 2 = \(\frac{-3}{4}\)(x-1)
4y + 8 = -3x + 3 ⇒ 3x + 4y + 5 = 0.
Question 9.
Find the equation of the diameter of the circle 2x2 + 2y2 + 3x – 5y – 1 = 0 which when produced passes through the point (-1,2).
Answer:
Given 2x2 + 2y2 + 3x – 5y – 1 = 0 & p = (-1,2)
⇒ x2 + y2 + \(\frac { 3 }{ 2 }\)x – \(\frac { 5 }{ 2 }\)y – \(\frac { 1 }{ 2 }\) = 0
c = \(\left(-\frac{3}{4}, \frac{5}{4}\right)\)
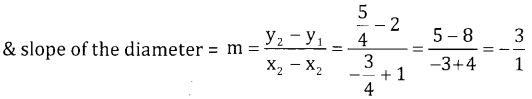
Equation of the diameter with p(-1,2), & m = -3.
y – y1, = m(x – x1); y – 2 = -3(x + 1); y – 2 = -3x – 3; 3x + y + 1 = 0.
![]()
Question 10.
Show that the line 4x – y=17 passes through the centre of the circle x2 + y2 – 8x + 2y=0.
Answer:
Given x2 + y2 – 8x + 2y = 0 & line 4x – y = 17 c = (4, -1)
C must lie on the line 4x – y = 17
4(4)-(-1) = 17
16 + 1 = 17 ⇒ 17 = 17
Hence the line 6x – y = 17 passes through the centre.
Question 11.
Find the length of the chord of the circle x2 + y2 – 6x + 15y – 16 = 0 intercepted by the x-axis.
Answer:
Given x2 + y2 – 6x + 15y – 6 = 0
C = \(\left(3, \frac{-15}{2}\right)\) & c = -16
Length intercepted by x – axis = 2\(\sqrt{g^{2}-c}\)
\(=2 \sqrt{(3)^{2}-(-16)}=2 \sqrt{9+16}=2 \sqrt{25}=10\)
∴ Length = 10 units
Question 12.
Find the length of the chord of the circle x2 + y2 + 3x – y – 6 = 0 intercepted by the y-axis.
Answer:
Given x2 + y2 + 3x – y – 6 = 0
c = \(\left(-\frac{3}{2}, \frac{1}{2}\right)\) C=-6
Length intercepted by y-axis = 2\(\sqrt{f^{2}-c}\)
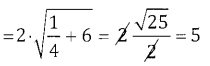
∴ Length = 10 units
Question 13.
Find the length of the chord of the circle x2 + y2 – 6x – 4y – 12 = 0 on the coordinate axes.
Answer:
Given x2 + y2 – 6x – 4y – 12 = 0
C = (3, 2) C = -12
Length intercepted by x-axis \(2 \sqrt{g^{2}-c}=2 \sqrt{9+12}=2 \sqrt{21}\) units
Length intercepted by y-axis = \(2 \sqrt{f^{2}-c}=2 \sqrt{4+12}=2 \sqrt{16}\) = 8units.
![]()
Part – C
2nd PUC Basic Maths Circles Ex 15.2 Five Marks Questions and Answers
Question 1.
Find the equation of the circle.
(a) Passing through the origin, having its centre on the x- axis and radius 2 units.
(b) Passing through (2, 3) having its centre on the x-axis and radius 5 units.
(c) Passing through the points (5, 1), (3, 4) and has its centre on the x – axis.
(d) Passing through the points (1, 2) and (2, 1) and has its centre on the y – axis.
(e) Passing through the points (0,5) and (6, 1) and has its centre on the line 12x + 5y = 25.
(f) Passing through the points (1, -4) and (5,2) and has its centre on the line x – 2y + 9 =0.
(g) Passing through the points (0, -3) and (0,5) and whose centre lies on x – 2y + 5 = 0.
(h) Passing through (1, 1) and (2, 2) and having radius 1.
Answer:
(a) Let A = (0,0), centre on x – axis ⇒ C = (-g, 0), r = 2 units
Required equation is x2 + y2 + 2gx + 2fy + c = 0
It passes their (0,0) ⇒ c = 0, r = \(\sqrt{g^{2}+f^{2}-c}\)
2 = \(\sqrt{g^{2}+0-0}\) ⇒ g = ±2
Equation of the circle is x2 + y2 ± 4x = 0.
(b) Let the general equation of the circle be x2 + y2 + 2gx + 2fy + c = 0.
It passes through (2,3) ⇒ (2)2 + (3)2 + 2g(2) + 2f(3) + c = 0
4g + 6f + c + 13 = 0 ….(1)
Centre (-g, -f) lies on x – axis ⇒ f = 0 …(2)
r = \(\sqrt{g^{2}+f^{2}-c}\) = 5 = \(\sqrt{g^{2}-c}\) = 25 = g2 – C.
⇒ g2 – 25 = c. ….(3)
Solving 1, 2 & 3 we get g2 – 25 + 4g + 13 = 0
g2 + 4g – 12 = 0
⇒ (g + 6) (g – 2) = 0 ⇒ g = -6 or 2
When g = -6, c = (-6)2 – 25 = 36 – 25 = 11
g = 2, c = (2)2 – 25 = 4 – 25 = -21 .
∴ The required circles are x2 + y2 – 12x + 11 = 0
x2 + y2 + 4x – 21 = 0.
![]()
(C) Let the required equation of the circle is x2 + y2 + 2gx + 2fy + c = 0
It passes through (5, 1) & (3, 4)
(5, 1) (5)2 + (1)2 + 2g(5) + 2f (1) +C = 0
10g + 2f + C + 26 = 0 …..(1)
(3,4) 32 + 42 + 2g (3) + 2f (4) +c= 0
68 + 8f + C + 25 = 0 …..(2)
& the centre (- g, – f) lies on x-axis ⇒ f = 0 ….(3)
Solving 1 & 2 we get
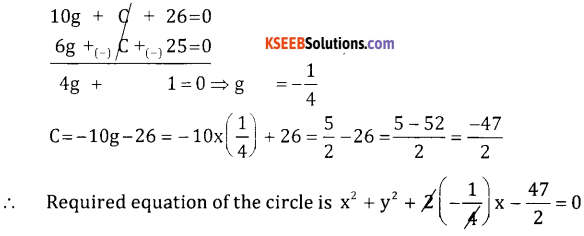
⇒ 2x2 + 2y2 – x – 47 = 0.
(d) Let required equation of the circle is x2 + y2 + 2gx + 2fy + c = 0
It passes through the points (1,2) & (2, 1) & centre lies on y-axis ⇒ g = 0 ….(1)
(1,2) 12 + 22 + 2g(1) + 2f(2) + c = 0 ⇒ 4f + C + 5 = 0 ….(2)
(2, 1) 22 + 12 + 2g(2) + 2f(1) + c = 0 ⇒ 2f+c + 5 = 0 ….(3)
Equation (3) – eqn. (2) gives 2f = 0 ⇒ f = 0
g = 0, f = 0 ⇒ c= -5
∴ Required equation of the circle is x2 + y2 – 5 = 0
(e) Let required equation of the circle is x2 + y2 + 2gx + 2fy + c = 0
It passes through (0,5) & (6, 1)
(0,5) 0 + 52 + 2g(0) + 2f(5) + c = 0
1f + C + 25 = 0 …(1)
(5, 1) 62 + 12 + 2g (6) + 2f (1) + c = 0
12g + 2f + c + 37 = 0 …..(2)
Centre (-g, -f) lies on the line 12x + 5y – 25 = 0
-12g – 5f – 25 = 0 ….(3)
Eqn. 2 – eqn. (1) gives
12g – 8f + 12 = 0 …..(4)
Adding 3 & 4 we get
12g – 13f – 13 = 0 ⇒ f = -1
From eqn (1) ⇒ 10(-1) + C + 25 = 0 ⇒ C = – 15
∴ -12g = 5f + 25
-12g = 20 ⇒ g = \(\frac{20}{-12}=\frac{-5}{3}\)
∴ The required equation of the circle is
x2 + y2 + 2\(\left(-\frac{5}{3}\right)\)x + 2(-1)y – 15 = 0 ⇒ × 3
3x2 + 3y2 – 10x – 6y – 45 = 0
![]()
(f) Let the required equation of the circle is x2 + y2 + 2gx + 2fy + c = 0 but it passes through (1,-4) & (5,2) & centre (-g, -f) lies on the line
⇒ -g + 2f + 9 = 0 …… (1)
(1,-4) 12 + (-4)2 + 2g(1) + 2f(-4) + c = 0
2g – 8f + C + 17 = 0 ….. (2)
⇒ (5,2) 52 + 22 + 2g(5) + 2f(2) +C = 0
10g + 4f + C+ 29 = 0 ….. (3)
Eqn. (3) – eqn. (2) gives 8g + 12f + 12 = () – 4
2g + 3f + 3 = 0 …..(4)
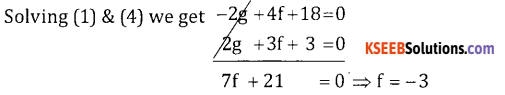
2f + 9 = g ⇒ g = -6 + 9 = 3
C = -2g + 8f – 17
C = -6 -24 – 17 = – 47
∴ The required equation of the circle is
x2 + y2 + 2 (3)x + 2 (-3)y – 47 = 0
x2 + y2 + 6x – 6y – 47 = 0
(g) Let the equation of required circle is x2 + y2 + 2gx + 2fy + c = 0 it passes
Through (0, -3) & (0,5) & centre (-g, -f)
Lies on the line x – 2y + 5 = 0 ⇒ -g + 2f + 5 = 0 …..(1)
(0,-3) 0 + 9 + (-6f) + c = 0
-6f + 9 + c = 0 …..(2)
(0,5) 0 + 25 + 0 + 10f + C = 0
10f + C + 25 = 0 …. (3)
∴ eqn. (3) – eqn. (2) gives 16f + 16 = 0 ⇒ f =-1
2f + 5 = g ⇒ g= -2 + 5 = 3
c = 6f – 9 = -6 -9 = -15 ⇒ c = -15
∴ The equation of the circle with g = 3, f = -1 & C = -15 is
x2 + y2 + 2 (3) x + 2 (-1)y – 15 = 0
x2 + y2 + 6x – 2y – 15 = 0
(h) Let the equation of the required circle is x2 + y2 + 2gx + 2fy + c = 0
If passes through (1, 1) & (2,2)
(1,1) 12 + 12 + 2g(1) + 2f(1) + c = 0
2g + 2f + C + 2 = 0 ….. (1)
(2, 2) 4 + 4 + 2g(2) + 2f (2) + c = 0
4g + 4f + c + 8 = 0 …… (2)
Also r = 1 ⇒ \(\sqrt{g^{2}+f^{2}-c}\) =1 ⇒ g2 + f2 – c = 1 …… (3)
Eqn. (2) – eqn. (1) gives 2g + 2f + 6 = 0
g + f + 3 = 0
g = (-3 -f) ….(4)
Adding 1 and 3 we get
g2 + f2 + 2g + 2f = -1
(-3 -f)2 + f2 + 2 (-3-f) + 2f + 1 = 0
![]()
2f2 + 6f + 4 = 0 ÷ 2
f2 + 3f + 2 = 0
(f + 2) (f + 1) = 0 ⇒ f = -1 or -2
When f = -2, g = -3-f = -3 + 2 = -1
When f = -1, g = -3-f = -3 + 1 = -2
C = g2+ f2 -1 = 1 + 4 – 1 = 4
∴ Required circles are x2 + y2 – 2x – 4y + 4 = 0 and x2 + y2 – 4x – 2y + 4 = 0.
![]()
Question 2.
Find the equation of the circle passing through the points.
(a) (0, 2), (3, 0), (3, 2)
(b) (1, 1), (-2, 2), (-6,0)
(c) (1, 1), (5,-5), (6,-4)
(d) (1, 0), (3,0), (0, 2)
(e) (5, 7), (6, 6), (2,-2)
(0) (p, q), (p, 0), (0,)
(g) (0, 1), (2,3), (-2,5)
(h) (0,0), (a,0), (0, b)
Answer:
(a) Let the required equation of the circle is x2 + y2 + 2gx + 2fy + c = 0
This equation passes through (*0,2) (3,0) & (3,2)
(0,2) 02 + 22 + 2g(0) + 2 f(2) + c = 0
4f + 4 + c = 0 …. (1)
(3,0) 6g + 9 + c = 0 …. (2)
(3,2) 6g + 4f + 13 + c = 0 …. (3)
Solving (1), (2), (3) we get
(2) – (1) gives g – 4f + 5 = 0
(3) – (2) gives 4f + 4 = 0 f = -1
6g = 4(-1) -5 = -9 ⇒ g =\(-\frac{9}{6}=-\frac{3}{2}\).
C = -4f – 4 = 4 – 4 = 0
∴ Required equation of the circle is
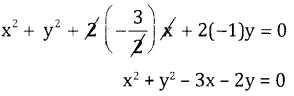
(b) (1, 1) (-2,2) (-6,0)
The general equation of the circle x2 + y2 + 2gx + 2fy +C = 0
This equation passes through (1, 1) (-2,2) & (-6,0)
(1, 1) 1 + 1 + 2g + 2f + c = 0
2g + 2f + 2 + c = 0 …. (1)
(-2,2) 4 + 4 – 4g + 4f + c = 0
-4g + 4f + 8 + c ….. (2)
(-6,0) 36 + 0 – 12g + c = 0
-12g + 36 + c = 0 …. (3)
(2) – (1) gives -6g + 2f + 6 = 0 … (4) × 2
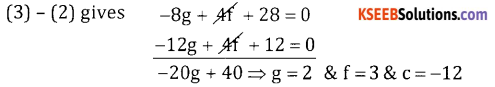
∴ The required eqn. is x2 + y2 + 4x + 6y – 12 = 0
![]()
(c) (1, 1) (5,-5) (6,-4)
The general equation of the circle
x2 + y2 + 2gx + 2fy + c = 0
This equation passes through (1, 1) (5,-5) (6, -4)
(1; 1) 2g + 2f + C + 2 = 0 ….. (1)
(5,-5) 10g – 10f + C + 50 = 0 …. (2)
(6,4) 12g + 8f + C + 52 = 0 …. (3)
(2)-(1) gives 8g – 12f + 48 = 0 ….. (4)
(3) – (2) gives 2g + 18f + 2 = 0 …. (5)
Solving (4) & (5) we get f = \(\frac { 10 }{ 11 }\) g = \(\frac { 111 }{ 21 }\) & C = \(-\frac { 284 }{ 21 }\)
∴ the required equation is
x2 + y2 + \(\frac { 222x }{ 21 }\) + \(\frac { 20y }{ 21 }\) – \(\frac { 284 }{ 21 }\) = 0 – × 21
21x2 + 21y2 + 222x + 20y – 284 = 0
(d) Let the general eqn, x2 + y2 + 2gx + 2fy + c = 0. The circle passes through the points
(1, 0) (3,0) & (0,2)
(1,0) 2g + C + 1 = 0 …. (1)
(0,2) 4f + C + 4 = 0 ….. (2)
(3,0) 6g + C + 9 = 0 …… (3)
Solving 1, 2, 3 we get g = -2, f = \(-\frac{7}{4}\) & c = 3
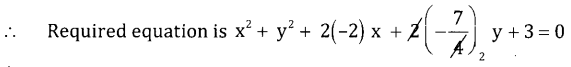
∴ 2x2 + 2y2 – 8x – 7y + 6 = 0.
![]()
(e) Let the general eqn. x2 + y2 + 2gx + 2fy + c = 0. The circle passes through the points
(5,7) (6, 6) (2,-2)
(5,7) 10g + 14f + 74 + c = 0 … (1)
(6,6) 12g + 12f + C + 72 = 0 …(2)
(2,-2) 4g – 4f + C + 8 = 0 …(3)
Solving 1, 2 and 3 we get g = -2, f = -3 & c= -12
∴ Required equation is x2 + y2 – 4x – 6y – 12 = 0.
(f) (p, q) (p, 0) (0,9)
Let the general eqn. x2 + y2 + 2gx + 2fy + c = 0.
The circle passes through the points
(p, q) (p, 0) (0,q)
(p, q) p2 + q2 + 2pq + 2qf + c = 0 … (1)
(p, 0) p2 + 2pg + c = 0 …… (2)
(0,q) q2 + 2qf + c= 0 … (3)
1 – 2 gives 2qf = -q2 ⇒ f = \(-\frac{q}{2}\)
1 – 3 gives 2pg = -p2 ⇒ g= \(-\frac{p}{2}\) & c = 0
∴ Required eqn. is x2 + y2 – px – qy = 0.
(g) Let the general eqn, x2 + y2 + 2gx + 2fy + c = 0. The circle passes through the points.
(0, 1) (2,3) (-2,5)
(0, 1) 2f + C = -1 ….. (1)
(2,3) 4g + 6 + c = -13 … (2)
(-2,5) -4g + 10f +c= -29 … (3)
Solving 1, 2, 3 we get g = \(\frac{1}{3}\) , f = \(-\frac{10}{3}\), c = \(\frac{17}{3}\)
∴ Required equation is x2 + y2 + \(\frac{2}{3}\)x – \(\frac{20}{3}\)y + \(\frac{17}{3}\) = 0
3x2 + y2 + 2x – 20y + 17 = 0
![]()
(h) Let the general equation x2 + y2 + 2gx + 2fy + c = 0. The circle passes through the points (0,0) (a, 0) (0, b)
(0,0) c = 0 …. (1)
(a,0) 2ag + c = -a2 ⇒ g = \(-\frac{a}{2}\)
(0, b) 2bf + c = -b2 ⇒ f = \(-\frac{b}{2}\)
∴ Required equation is x2 + y2 – ax – by = 0.
Question 3.
Find the equations of the circles whose radius is 5 and which passes through the points on X-axis at distances 3 from the origin.
Answer:
Given r = 5, passes through points on x-axis at a distance 3 from the origin
⇒ The points are (3,0) and (-3,0)
Let x2 + y2 + 2gx + 2fy + c = 0 is required equation
(3,0) 6g + C + 9 = 0 … (1)
(-3,0) -6g + C + 9 = 0 …. (2)
r = 5; 25 = g2 + f2 -C
Adding 1 and 2 we get c = -9 and g = 0 and f = ±4
∴ The required equation is x2 + y2 + 8y – 9 = 0
Question 4.
A circle has radius 3 units and its centre lies on the line y = x – 1. Find the equation of the circle if it passes through (7,3).
Answer:
Given r = 3 and centre (-g,-f) lies on y = x – 1
⇒ -f = -g -1
g – f + 1 = 0 …. (1)
Equation passes through (7,3) ⇒ 14g + 6f + C + 58 = 0 …. (2)
r = 3 ⇒ r2 = g2 + f2 -c = 9 … (3)
Solving 1, 2, 3 we get g = -7 or g = -4, c = 76
f = -6 or g = -3, c = 16
∴ We get two equations of circles
x2 + y2 -14x – 12y + 76 = 0
x2 + y2 – 8x – 6y + 16 = 0.
![]()
Question 5.
Find the equation of the circle cuts intercepts of the length ‘a’ and ‘b’ on axes and passes through the origin
Answer:
Intercepts a and b on axes that implies circle passes through the points (a, 0) and (0, b) passing through origin
⇒ c = 0
(a, 0) a2 + 2ga = 0 ⇒ g = \(-\frac{a}{2}\)
(0, -b) b2 + 2fb = 0 ⇒ f = \(-\frac{b}{2}\)
∴ The required equation is x2 + y2 – ax – by = 0.
Question 6.
Find the equation of the circle passing through the origin and lengths ‘a’ and ‘b’ on axes and passing through the origin.
Answer:
Positive x-intercept a i.e., (a,0)
Negative y-intercept bi.e., (0, -b)
Let x2 + y2 + 2gx + 2fy + c = 0 passes through origin ⇒ c = 0 …. (1)
(a,0) ⇒ a2 + 2ga = 0 = g ⇒ \(-\frac{a}{2}\) .. (2)
(0, -b) ⇒ b2 – 2fb = 0 = f ⇒ \(-\frac{b}{2}\) … (3)
∴ The required equation is x2 + y2 – ax + by = 0.
Question 7.
Find the length of the chord intercepted by the
(a) circle x2 + y2 – 8x – 6y = 0 and the line x – 7y – 8 = 0
(b) circle x2 + y2 = 9 and the line x + 2y = 3
(c) circle x2 + y2 – 6x – 2y + 5 = 0 and the line x – y+ 1 = 0
Answer:
(a) Given centre (4,3)
r= \(=\sqrt{16+9}=\sqrt{25}\) = 5
P = length of the perpendicular from (4, 3) to the line x – 7y – 8 = 0
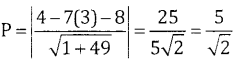
Length of the chord = 2 . \(\sqrt{r^{2}-p^{2}}\)
\(=2 \sqrt{5^{2}-\left(\frac{5}{\sqrt{2}}\right)^{2}}=2 \sqrt{25-\frac{25}{2}}=2 \sqrt{\frac{50-25}{2}}=2 \cdot \frac{5}{\sqrt{2}}\)
L = 5\(\sqrt{2}\) units
![]()
(b) Centre (0,0), r = 3, Line x + 2y – 3 = 0
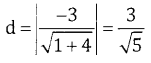
Length of the chord = \(2 \cdot \sqrt{r^{2} \cdot d^{2}}=2 \sqrt{9-\frac{9}{5}}=2 \sqrt{\frac{36}{5}}=\frac{12}{\sqrt{5}}\) units
(c) Centre = (3, 1) and r = \(\sqrt{9+1-5}=\sqrt{5}\) , line x – y + 1 = 0
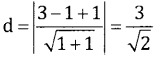
Length of the chord = \(2 \sqrt{r^{2}-d^{2}}=2 \sqrt{5-\frac{9}{2}}=2 \cdot \frac{1}{\sqrt{2}} 5 \text { units }\)
Question 8.
Find the points of intersection of the circle.
(a) x2 + y2 = 9 and the line x + 2y = 3.
(b) x2 + y2 – 6x – 2y + 5 = 0 and the line x – y + 1=0.
(c) x2 + y2 + 4x + 6y – 12 = 0 and the line x + 4y – 6 = 0
Also find the length of the chord.
Answer:
(a) Given x = 3 – 2y and x2 + y2 = 9
(3 – 2y)2 + y2 = 9
5y2 – 12y = 0
y(5y – 12) = 0 ⇒ y = 0, y = 12
⇒ x = 3, x = \(-\frac{9}{5}\)
The points are (3, 0) and \(\left(-\frac{9}{5}, \frac{12}{5}\right)\)
∴ Length of the chord = \(\sqrt{\left(3+\frac{9}{5}\right)^{2}+\left(\frac{12}{5}\right)^{2}}=\frac{\sqrt{720}}{5}\)
(b) Given
x + 1 = y and x2 + y2 – 6x – 2y + 5 = 0
x2 + (x + 1)2 – 6x – 2 (x + 1) + 5 = 0
2x2 – 6x + 4 = 0
x2 – 3x + 2 = 0
(x – 2)(x – 1) = 0 = x= 2 or 1
When x = 2, y = 3 and when x = 1, y = 2
∴ The points are (2, 3) and (1, 2) and length of the chord
= \(\sqrt{(2-1)^{2}+(3-2)^{2}}=\sqrt{1+1}=\sqrt{2}\)
![]()
(c) Given x = 6 – 4y and x2 + y2 + 4x + 6y – 12 = 0
(6 – 4y)2 + y2 + 4 (6 – 4y) + 6y – 12 = 0
17y2 – 58y + 48 = 0
17y2 – 34y – 24y + 48 = 0
17y (y – 2) – 24 (y – 2) = 0
(y – 2) (17 y – 24) = 0 ⇒ y = 2 or
When y = 2, x = 6 – 4y = 6 – 8 = -2
When y = \(\frac { 24 }{ 17 }\) x = \(6-\frac{96}{17}=\frac{102-96}{17}=\frac{6}{17}\)
∴ The points are (-2,2) and \(\left(\frac{6}{17}, \frac{24}{17}\right)\)
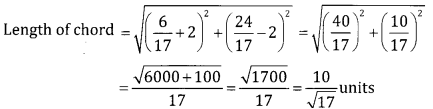
Part-D
2nd PUC Basic Maths Circles Ex 15.2 Six Marks Questions and Answers
Question 1.
Show that the following points are concylie.
(a) (0, 0), (1, 1), (5, -5), (6,-4)
(b) (2,-4), (3, -1), (3,-3), (0,0)
(c) (1.0), (2, -7), (8, 1), (9,-6)
Answer:
(a) First find the equation of the circle passing through the points (0,0) (1, 1) (5,-5) (6, -4)
(0,0) ⇒ C = 0 …. (1)
(1, 1) ⇒ 2g + 2f + 2 = 0 …. (2)
(5,-5) ⇒ 10g -10f + 50 + c = 0 …. (3)
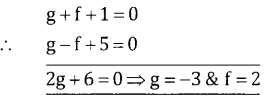
∴ The equation of the circle is x2 + y2 – 6x + 4y = 0
Substituting the fourth point (6,-4) we get
36 + 16 – 36 – 16 = 0 ⇒ 0 = 0
∴ The points are concyclic.
(b) Let us find the equation of the circle passing through (2,-4) (3,-1) and (3, -3) we get
(2,-4) 4g – 8f + C + 20 = 0 … (1)
(3,-1) 6g – 2f+ C + 10 = 0) … (2)
(3,-3) 6g – 6f+c= -18 … (3)
Solving the above equations we get g = -1, f = 2 and C = 0
∴ Required circle is x2 + y2 – 2x + 4y = 0
Substitute the fourth point (0,0), we get 0 + 0 + 0 + 0 = 0
∴ The four points are concyclic
![]()
(c) Let us find the equation of the circle passing through (1, 0) (2, -7) and (8, 1) we get
(1,0) 2g + C + 2 = 0 … (1)
(2,-7) 4g – 14f + C + 53 = 0 … (2)
(8,1) 16g + 2F + C + 25 = 0 … (3)
Solving above 3 equations we get g = \(-\frac { 738 }{ 50 }\),f = \(\frac { 147 }{ 50 }\) and c = \(\frac { 196 }{ 25 }\)
∴ Required circle is x2 + y2 + \(\frac{246}{50} x\) + \(\frac{147}{25} y\) + \(\frac{196}{25} \) = 0
25x2 + 25y2 + 246 x + 147 y + 196 = 0
Substitute the fourth point (9,-6) we get
25(9)2 + 25(-6)2 + 246 (9) + 147 (-6) + 196 = 0
2025 + 900 + 2214 – 882 + 196 0
The points are not concyclic