Students can Download Basic Maths Exercise 16.1 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 16 Parabola Ex 16.1
Part – A
2nd PUC Basic Maths Parabola Ex 16.1 One or Two Marks Questions and Answers
Question 1.
Write the characteristics of the following parabolas.
(a) y2 = 16x
(b) y2 = -8x
(c) 3x2 = -8y
(d) x2 = 8y
(e) y2 = 8x
(f) y2 + 4x = 0
(g) 3x2 + 4y = 0
(h) x2 + 4x = 0
Answger:
(a) Compare y2 = 16x with y2 = 4ax
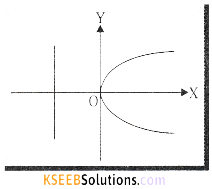
We get 4a = 16 ⇒ a = 4
The curve turns right side with vertex (0,0)
Focus S(a,0) = (4,0)
Directrix x = -a or x = -4 or x + 4 = 0
Axis x-axis (equation is y = 0)
Tangent y-axis (equation is x = 0)
Equation of LR is x = a ⇒ x = 4 or x – 4 = 0
Length of LR 4a = 16
Ends of LR (a, 2a) (a, -2a) = (4,8) and (4,-8)
![]()
(b) y2 = -8x compare with y2 = -4ax
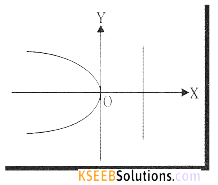
The curve turns left hand side and 4a = 8 ⇒ a = 2
Vertex = (0,0)
Axis x-axis (equation is y = 0)
Tangent y-axis (equation is x = 0)
Focus S(-2,0)
Directrix, x = 2 or x – 2 = 0
Equation of LR x = -2 or x + 2 = 0
Length of LR = 4a = 8
Ends of LR (-a, 2a) (-a, -2a) = (-2, 4) (-2,-4)
(C) 3x2 = -8y ⇒ x2 = \(\frac {-8 }{ 3 }\) y compare this with
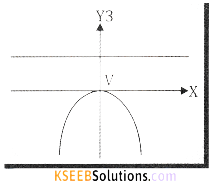
x2 = -4ay ⇒ 4a = \(\frac { 8 }{ 3 }\) ⇒ a = \(\frac { 2 }{ 3 }\)
The curve turns downwards
Vertex V = (0,0)
Axis y-axis (equation is x = 0)
Focus S = \(\left(0,-\frac{2}{3}\right)\)
Tangent x-axis (equation is y = 0)
Directrix y = \(\frac { 2 }{ 3 }\) = or 3y – 2 = 0
Equation of LR y = –\(\frac { 2 }{ 3 }\) or 3y + 2 = 0
Length of LR = 42 = \(\frac { 8 }{ 3 }\) ; Ends of LR \(\left(\frac{4}{3},-\frac{2}{3}\right)\left(-\frac{4}{3},-\frac{2}{3}\right)\)
![]()
(d) x2 = 8y compare this with x2 = 4ay the curve turns upwards
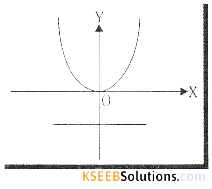
4a = 8 ⇒ a = 2
Vertex, V = (0,0)
Axis y-axis (equation is x = 0)
Tangent x-axis (equation is y = 0)
Directrix y = -2 or y + 2 = 0
Equation of LR y = 2 or y – 2 = 0
Length of LR 4a = 8
Ends of LR (4, 2) (-4, 2)
(e) y2 = 8x compare with y2 = 4ax. The curve turns right side
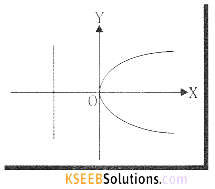
4a = 8 ⇒ a = 2
Vertex, V = (0,0)
Axis, x-axis (equation is y = 0)
Tangent, y-axis (equation is x = 0)
Focus S = (2,0)
Directrix x = -2 or x + 2 = 0
Equation of LR x = 2
Length of LR 4a = 8
Ends of LR (2, 4) (2,-4)
![]()
(f) Compare y2 = -4x with y2 = -4ax. The curve turns
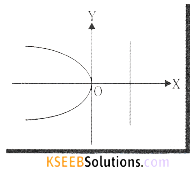
Left hand side
4a = 4 ⇒ a = 1
Vertex, V = (0,0)
Axis x-axis (equation is y = 0)
Tangent y-axis (equation is x = 0)
Directrix, x = 1 or x = -1 = 0
Equation of LR x = -1 or x + 1 = 0
Ends of LR (-1,2) (-1, -2)
Length of LR = 4a = 4
(g) 3x2 + 4y = 0
x2 = \(\frac{-4}{3} y\) compare with x2 = – 4ay.
The curve turns downwards and 4a = \(\frac { 4 }{ 3 }\) ⇒ a = \(\frac { 1 }{ 3 }\)
Vertex, V = (0,0)
Axis y-axis (equation is x = 0)
Tangent x-axis (equation is y = 0)
Focus, s=(0,- \(\frac { 1 }{ 3 }\)) Directrix y = \(\frac { 1 }{ 3 }\) or 3y – 1=0
Equation of LR y = \(\frac { -1 }{ 3 }\) or 3y +1=0 Length of LR = 4a = \(\frac { 4 }{ 3 }\)
Ends of LR \(\left(-\frac{2}{3},-\frac{1}{3}\right)\left(\frac{2}{3},-\frac{1}{3}\right)\)
![]()
(h) x2 + 16y = 0 compare with x2 = -4ay
x2 = -16y. The curve turns downward
4a = 16 ⇒ a = 4
Vertex, V = (0,0)
Axis y-axis (Equation is x = 0)
Tangent x-axis (Equation is y = 0)
Focus, S = (0, -4)
Directrix y = 4 or y – 4 = 0
Equation of LR y = -4 or y + 4 = 0
Length of LR = 4a = 16
Ends of LR (-8,-4) (8,-4).
Question 2.
If the length of the latus rectum of y2 = 8kx is 4 find k
Answer:
Compare y2 = 8kx with y2 = 4ax
We get 4a = 8k ⇒ a = 2k
Given length of LR = 4
4a = 4 ⇒ 8k = 4 ⇒ k = \(\frac { 1 }{ 2 }\)
Question 3.
If the length of the latus rectum of x2 = 4ky is 8, find the value of k.
Answer:
Compare x2 = 4ky with x2 = 4ay.
We get 4k = 4a ⇒ a=k
Given length of LR = 8
4a = 8
4k = 8
k = 2.
![]()
Part-B
2nd PUC Basic Maths Parabola Ex 16.1 Two or Three Marks Question and Answers
Question 1.
Find the equation of the parabola given that its.
(a) Vertex is (0,0) and focus is (4,0)
(b) Vertex is (0,0) and directrix is y = – 3
(c) Focus is (1,0) and directrix is x = – 1,
(d) Focus is (-4, 0) and directrix is x = 4
(e) Focus is (0, -3) and directrix is y=3
(f) Focus is (0, 6) and vertex is (0,0)
(g) Vertex is (0,0), axis is y axis and passes through \(\left(\frac{1}{2}, 2\right)\)
(h) Vertex is (0,0) axis is y axis and passes through (-1, -3)
Answer:
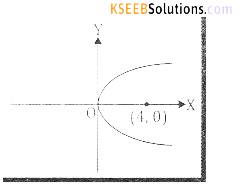
(a) Given V = (0,0) and Focus, S = (4,0)
It is a right handed parabola with
a = 4 and standard form is
y2 = 4ax
Put a = 4, then
y2 = 16x.
![]()
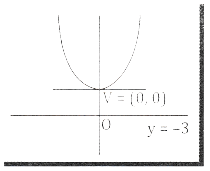
(b) Given V = (0,0) and directrix = y = -3
Focus = (0,3) ⇒ a = 3
It is a upward parabola and
standard form is x2 = 4ay
Put a = 3, x2 = 4.3y
⇒ x2 = 12y
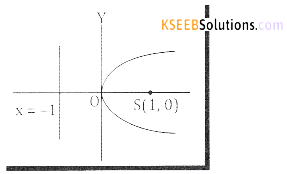
(C) Given Focus = S = (1,0) and directrix is
x =-15 ⇒ a = 1
it is a right handed parabola
and standard form is y2 = 4ax put a = 1
⇒ y2 = 4x
![]()
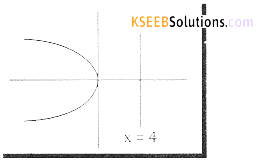
(d) Give Focus = S = (-4, 0) and directrix
is x = 4; S = (-4,0) ⇒ a = 4
It is a left handed parabola standard
form is y2 = -4ax put a = 4
we get y2 = -16x
(e) Given focus is (0, -3) and directrix is y = 3
⇒ a = 3 and curve turns
downwards and standard form is
x2 = -4ay put a = 3,
we get x2 = -12y
![]()
(f) Given focus S = (0,6) and Vertex, V = (0,0)
⇒ a = 6 and it is a upward parabola and
the standard form is x2 = 4ay
Put a = 6
We get x2 = 24y
(g) Given vertex V = (0,0) and axis is y-axis and it passes through \(\left(\frac{1}{2}, 2\right)\)
which is in I quadrant
∴ it is a upward parabola
x2 = 4ay put x = \(\frac { 1 }{ 2 }\) and y = 2; \(\frac { 1 }{ 4 }\) = 4a 2 ⇒ \(\frac { 1 }{ 4 }\) = 8a ⇒ a = \(\frac { 1 }{ 32 }\)
∴ The required equation is x2 = 4ay
x2 =4. \(\frac{1}{32} y\) ⇒ x2 = \(\frac{1}{8} y\) or 8x2 – y = 0
(h) Vertex, V(0, 0) and y-axis and it passes through the point (-1, -3)
which is in third quadrant
∴ It is a downward parabola,
i.e., x2 = -4ay
put x=-1 and y = -3; (-1)2 = -4a(-3)
1 = 12a ⇒ a = \(\frac { 1 }{ 12 }\)
∴ Required equation is x2 = -4ay
x2 = -4.\(\frac { 1 }{ 12 }y\) ; 3x2 + y = 0.
![]()
Part – C
2nd PUC Basic Maths Parabola Ex 16.1 Five Mark Questions and Answers
Question 1.
Define parabola and with usual notation Prove that y2 = 4ax geometrically
Sol.
Definition of Parabola and other forms of parabola
Parabola is a conic section whose eccentricity is 1. That is, Parabola is the locus of the point which moves such that its distance from the fixed point (called the focus) is equal to its distance from the fixed line (called the directrix) We shall derive the equation of the parabola in its standard form.
Theorem: The equation of a Parabola with proper choice of co-ordinates axes is y2 = 4ax
Proof: Let S be the focus and the line l be the directrix. Draw SZ through S and perpendicular to the directrix. Let O be the midpoint of the line segment SZ.
Let SZ = 2a (a > 0) ⇒ OZ = OS = a
We shall choose 0 as the origin and the line ZOS as x axis.
The line YOY’ through O, perpendicular to the x-axis will be y-axis.
With this choice of co-ordinate axes we have S(a, o) and Z(-a, 0)
The equation of the directrix is l is x = -a
Let P(x,y) be any point on the Parabola. Then by the definition of the Distance of P
from S = Distance of P from the line ‘l’.
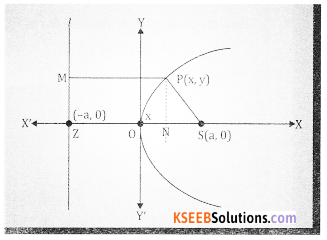
|SP| = |PM|
SP2 = ZN2 since PM = ZN
SP2 = (OZ + ON)2
(x – a)2 + y2 = (a + x)2 (|OZ| = a, |ON| = x)
x2 – 2ax + a2 + y2 = a2 + 2ax + x2
y2 = 4ax which is the equation of the parabola.
![]()
Note:
The equation y2 = 4ax is also called standard form of the equation of the parabola.
Shape of the Parabola y2 = 4ax
We shall note few observations from the equation y2 = 4ax, which will help us to trace the curve parabola.
1. Ify is replaced by -y in the equation remains same, i.e., (-y)2 = 4ax → y2 = 4ax. This shows that if (x, y) is any point on the curve y2 = 4ax, then (x, -y) is also a point on the curve. Thus, the curve is symmetric about the x – axis, i.e., the shape of the curve above the x axis is the mirror image (about the x axis) of the shape of the curve below the x – axis.
2. If x < 0, then y will be a negative quantity (note that a > 0) and therefore y2 = 4ax will have no real solution for y. This shows that no part of the curve lies to the left side of the x-axis.
3. If y =0, the only value of x we get is zero. Thus the curve cuts the x axis at the origin(0,0)
4. If x = 0, we get y2 = 0, which gives y = 0. Thus the curve cuts the y-axis at the origin and further the y-axis meets the curve only at the origin. That is, y – axis is a tangent to the curve at the origin.
5. For any point P(x, y) on the parabola we have
y2 = 4ax ⇒ y = ±2\(\sqrt{\mathrm{ax}}\)
y = 2\(\sqrt{\mathrm{ax}}\) and y = -2\(\sqrt{\mathrm{ax}}\)
This shows that, as x increases from 0 to ∞, y also increases from 0 to ∞ or y decreases from 0 to -∞. Thus, the two branches of the parabola, laying on opposite sides of the x – axis, will extend to infinity towards the positive directions of the x – axis.
From the above discussion and by plotting few points, whose coordinates satisfy y2 = 4ax, it is found the shape of the parabola is as shown in the following figure.
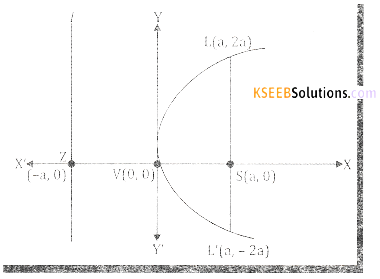
![]()
The origin 0 is called the Vertex of the parabola, y2 = 4ax, it is also denoted by V(0,0).
The line ZSX is called the axis of the parabola and its equation is y = 0
The focus S (a,0) and the equation of the directrix is x – a i.e., X + a = 0 They – axis is called the tangent at the vertex – its equation is x = 0.
Note:
The distance between the vertex and the focus is the distance between the vertex and the directrix is equal to a and the distance between the directrix and the focus is 2 a.
Definition:
The chord passing through the focus and perpendicular to the axis of the parabola is called the latus rectum of the parabola.
In the figure LSL1 is the latus rectum.
The points L and L1 on the parabola are called end points of the latus rectum, the length is called the length of the latus rectum.
Clearly, the x – coordinates of L and L’ is a because OS = a. To find the corresponding coordinates, we shall put x = a in y2 = 4ax, we get y = ±2a. Thus, y – coordinates of L and L1 respectively.
L = (a, 2a) and L1 = (a, -2a)
∴ consider |LL’| = \(\sqrt{(a-a)^{2}+(2 a+2 a)^{2}}=\sqrt{(4 a)^{2}}=4 a\)
Thus, the length of the latus rectum, LL1 = 4a.
Note :
Any chord passing through the focus is called a focal chord. Focal chord need not be perpendicular to the axis of the parabola