2nd PUC Basic Maths Question Bank Chapter 18 Differential Calculus Ex 18.1

Students can Download Basic Maths Exercise 18.1 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Basic Maths Question Bank Chapter 18 Differential Calculus Ex 18.1

Part-A

2nd PUC Basic Maths Differential Calculus Ex 18.1 One Mark Questions and Answers

Question 1.
5e^x – log x – 3\(\sqrt{x}\)
Answer:
Let y = 5e^x – log x – 3\(\sqrt{x}\)
\(\frac{d y}{d x}=5 e^{x}-\frac{1}{x}-3 \frac{1}{2 \sqrt{x}}\)

Question 2.
log e^x
Answer:
Let y = log_e^e (constant)
\(\frac{d y}{d x}\) = 0

Question 3.
\(\frac{1}{x^{4 / 3}}-\frac{3}{x^{3 / 2}}\)
Answer:

Question 4.
\(\frac{4 x^{2}-3 x}{x}\)
Answer:
Let y = \(\frac{4 x^{2}}{x}-\frac{3 x}{x}\) = 4x – 3
∴ \(\frac{d y}{d x}\) = 4(1) – 0 = 4

Question 5.
\(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^{2}\)
Answer:

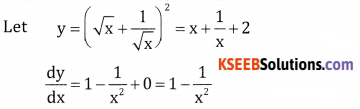
Question 6.
\(\sqrt[3]{x^{2}}+\frac{4}{\sqrt[4]{x^{5}}}+\frac{1}{x^{7}}+x \sqrt{x}\)
Answer:

Part-B

2nd PUC Basic Maths Differential Calculus Ex 18.1 Two Marks Questions and Answers

Question 1.
(x – a)(x – b).
Answer:
Let (x – a) (x – b)
\(\frac{d y}{d x}\) = (x – a) . 1 + (x – b) . 1 = x – a + x – b = 2x – a – b

Question 2.
\(\frac{x-a}{x-b}\)
Answer:
Let y = \(\frac{x-a}{x-b}\)

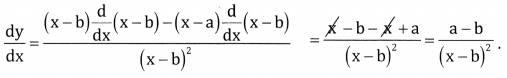
Question 3.
(5x² + 3x – 1) ( x – 1)
Answer:
Let y = (5x² + 3x – 1) ( x – 1)
\(\frac{d y}{d x}\) = (5x² + 3x – 1) \(\frac{d }{d x}\) (x – 1) + (x – 1) \(\frac{d }{d x}\) (5x² + 3x – 1)
= (5x² + 3x – 1) + (x – 1) (10x + 3) = 5x² + 3x – 1 + 10x² – 10x + 3x – 3 = 15x² – 4x – 4

Question 4.
x^-3(5 + 3x)
Answer:
let y = x^-3(5 + 3x)
\(\frac{d y}{d x}\) = x^-3(3) + (5 + 3x) (-3 . x^-3-1)
= 3x^-3 – 15x^-4 -9x^-3
= -15x^-4 – 6x^-3
= \(\frac{-3}{x^{4}}(2 x+5)\)

Question 5.
x⁵(3 – 6x^-9).
Answer:
Let y = x⁵(3 – 6x^-9)
\(\frac{d y}{d x}\) = x⁵(+54x^-10) + (3 – 6x^-9)(5x⁴)
= 54x^-5 + 15x⁴ – 30x^-5
= 24x^-5 + 15x⁴

Question 6.
sin²x.
Answer:
Let y = (sin x)²
\(\frac{d y}{d x}\) = 2 sin x .(cos x) = sin 2x

Question 7.
\(\frac{x+1}{x}\)
Answer:

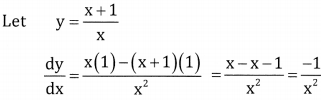
Question 8.
\(\frac{1}{a x^{2}+b x+c}\)
Answer:

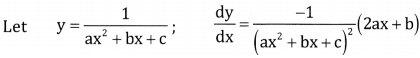
Question 9.
\(\frac{\cos x}{1+\sin x}\)
Answer:

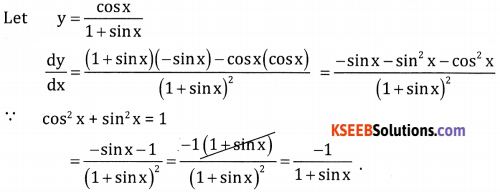
Question 10.
(x + cos x) ( x – tan x).
Answer:
Let y = (x + cos x)( x – tan x)
\(\frac{d y}{d x}\) = ( x + cosx)(1 – sec²x) + ( x tanx)(1 – sinx).

Question 11.
If f(x) = x² – 3x + 10. Find f'(50) and f'(11).
Answer:
Let f(x) = x² – 3x + 10
then f'(x) = 2x – 3
f'(50) = 100 – 3 = 97
f'(11) = 22 – 3 = 19

Question 12.
If f(x) = xⁿ and if f ‘(1) = 10. Find the value of n.
Answer:
f(x) = xⁿ and f¹(1) = 10
f ‘(x) = n. x^n-1; f ‘(1) = 10 = n.(1)^n-1 ⇒ n = 10

Question 13.
If y = \(x+\frac{1}{x}\) show that x² \(\frac{d y}{d x}\) – xy + 2 = 0
Answer:
Let y = \(x+\frac{1}{x}\)
\(\frac{d y}{d x}=1-\frac{1}{x^{2}}=\frac{x^{2}-1}{x^{2}} \Rightarrow x^{2} \frac{d y}{d x}=x^{2}-1\)
[∵ x² + 1 = xy]
[ x² = xy – 1]
⇒ x² \(\frac{d y}{d x}\) = xy – 1 – 1
⇒ x² \(\frac{d y}{d x}\) = xy + 2 = 0

Part-C

2nd PUC Basic Maths Differential Calculus Ex 18.1 Three Marks Questions and Answers

Question 1.
\(\frac{x^{5}-\cos x}{\sin x}\)
Answer:

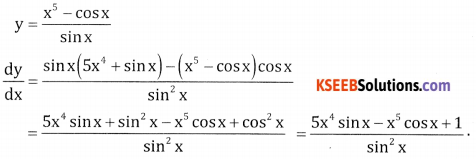
Question 2.
\(\frac{x^{n}-a^{n}}{x-a}\)
Answer:

Question 3.
\(\frac{2}{x+1}-\frac{x^{2}}{3 x-1}\)
Answer:

Question 4.
\(\frac{\sqrt{a}+\sqrt{x}}{\sqrt{a}-\sqrt{x}}\)
Answer:

Question 5.
\(\frac{2^{x} \log x}{\sqrt{x}}\)
Answer:

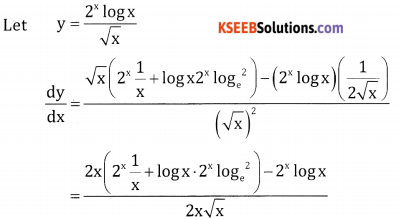
Question 6.
Find the derivative of f(x) = \(\frac { 1 }{ x }\) wit respect to x from the first principle.
Answer:

Question 7.
If y = x + tan x. Show that cos²x . \(\frac{d y}{d x}\) = 2 – sin²x
Answer:
Given y = x + tan x
\(\frac{d y}{d x}\) = 1 + sec² x = 1 + \(\frac{1}{\cos ^{2} x}=\frac{\cos ^{2} x+1}{\cos ^{2} x}\)
∴ cos²x \(\frac{d y}{d x}\) = cos²x + 1 = 1 – sin²x + 1 = 2 – sin²x
∴ cos²x \(\frac{d y}{d x}\) = 2 – sin²x