Students can Download Basic Maths Exercise 19.1 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 19 Application of Derivatives Ex 19.1
Part-A
2nd PUC Basic Maths Application of Derivatives Ex 19.1 Two Marks Questions and Answers
Question 1.
The displacement ‘s’ of a particle at time ‘t’ is given by S = 4t3 – 6t2 + t – 7. Find the velocity and acceleration when t = 2 sec.
Answer:
Given S = 4t3 – 6t + t – 7
Velocity = v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 12t2 -12t + 1
At t = 2secs, v = 12(2)2 – 12(2) + 1 = 48 – 24 + 1 = 25 units/sec.
At t = 2 sec, acceleration = 24.2 – 12 = 48 – 12 = 36 units/sec2.
Question 2.
If S = 5t2 + 4t – 8. Find the initial velocity and acceleration, (s = displacement, t = time).
Answer:
Given s = 5t2 + 4t – 8
V = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 10t + 4 dt
Initial velocity is velocity when t = 0
i.e., = 10.0 + 4 = 4 units/sec.
Acceleration = \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 10 units /sec2.
![]()
Question 3.
A stone thrown vertically upward rises ‘s’ ft. in ‘t’ sec. where s = 80t – 16t2. What its velocity after 2 sec.? Find the acceleration?
Answer:
Given S = 80t -16t2
v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 80 – 32t
At t=2 sec, v = 80 – 32 (2)
= 80 – 64 = 16 ft./sec.
Acceleration = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = -22 ft/sec2 .
Question 4.
A body is thrown vertically upwards its distance S feet is’t’ sec. is given by S = 5 + 12t – t2. Find the greatest highest by the body.
Answer:
Given s = 5 + 12t – t2
v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 12 – 2t dt
Maximum height ⇒ Kinetic energy = 0 ⇒ v = 0 ⇒ 12 – 2t = 0 ⇒ t = 6 sec
∴ Greatest height = s = 5 + 12.6 – 62
= 5 + 72 – 36 = 77 – 36 = 41 feet.
Question 5.
If v = \(\sqrt{s^{2}+1}\) prove that acceleration is ‘S’ (V = velocity, S = displacement).
Answer:
Given v = \(\sqrt{s^{2}+1}\)
Acceleration = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = \(\frac{1}{2 \sqrt{s^{2}+1}} \cdot 2 s \frac{d s}{d t}=\frac{1}{2 v}\) . 2 . s . v . s units / sec2.
Question 6.
If S = at3 + bt. Find a and b given that when t = 3 velocity is ‘O’ and the acceleration is 14 unit. (S = displacement, t = time).
Answer:
Given s = at3 + bt; v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 3at2+b
Acceleration = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 6at
When v = 0 then 3at2 + b = 0 ⇒ 27a + b = 0.
t = 3 sec
When acceleration = 14 then 14 = 6a.3, b = -27a = \(-\frac{27.7}{9}\) = -21
F = 3 sec. a = \(\frac{14}{18}=\frac{7}{9}\)
∴ a = \(\frac { 7 }{ 9 }\) and b = -21.
Question 7.
When the brakes are applied to moving car, the car travels a distance ‘s’ ft. in ‘t’ see given by s = 8t – 6t2 when does the car stop?
Answer:
Given s = 8t – 6t2
v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 8 – 12t car stops when v = 0
∴ 8 – 12t = 0 ⇒ t = \(\frac{8}{12}=\frac{2}{3}\) sec.
![]()
Part-B
2nd PUC Basic Maths Application of Derivatives Ex 19.1 Three Marks Questions and Answers.
Question 1.
The radius of sphere is increasing at the rate of 0.5 mt/sec. Find the rate of increase of its surface area and volume after 3 sec.
Answer:
Given \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 0.5 , t = 3 sec, \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = ? \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = ?
surface area = s = 4πr2
\(\frac{d s}{d t}\) = 4π . 2r . \(\frac{d r}{d t}\)
= 4π × 2 × 1.5 × 0.5
= 6π m2/sec
dr = 0.5 × dt
⇒ r = 0.5 t
= 0.5 × 3
= 1.5
Question 2.
The surface area of a spherical bubble is increasing at the rate of a 0.8cm2 / sec. Find at what rate is its volume increasing when r = .25cm [r = radius of the sphere].
Answer:
Given \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 0.8 cm2 / sec. r = 2.5 cm, \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = ?
s = 4πr2
\(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 4π . 2r × \(\frac{\mathrm{dr}}{\mathrm{dt}}\)
0.8 = 4π × 2 × 2.5. \(\frac{\mathrm{dr}}{\mathrm{dt}}\) ⇒ \(\frac{0.8}{8 \pi \times 2.5}=\frac{0.1}{2.5 \pi}\)
v = \(\frac { 4 }{ 3 }\)πr3
\(\frac{d v}{d t}=\frac{4}{3} \pi 3 r^{2} \cdot \frac{d r}{d t}=4 \pi \times(2.5)^{2} \times \frac{0.1}{2.5 \pi}=1 \mathrm{cc} / \mathrm{sec}\)
Question 3.
A spherical balloon is being inflated at the rate 35cc/sec. Find the rate at which the surface area of the balloon increases when its diameter is 14cm.
Answer:
Given \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 35cc /sec 2r = 14 ⇒ r = 7, \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = ?, \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = ?
v = \(\frac { 4 }{ 3 }\)πr3 s = 4πr2
\(\frac{d V}{d t}=\frac{4}{3} \pi 3 r^{2} \frac{d r}{d t} \quad \frac{d S}{d t}=4 \pi 2 r \frac{d r}{d t}\)
35 = 4π . 72 \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 4π × 2 × 7 × \(\frac{5}{28 \pi}\)
\(\frac{d r}{d t}=\frac{35}{196 \pi}=\frac{5}{28 \pi}=10 \mathrm{cm}^{2} / \mathrm{sec}\)
Question 4.
The radius of a circular plate is increasing at the rate of \(\frac{2}{3 \pi}\) cm/sec. Find the rate of change of its area when the radius is 6cm.
Answer:
Given \(\frac{d r}{d t}=\frac{2}{3 \pi} r=6 \mathrm{cm} \frac{d A}{d t}=?\)
A = πr2
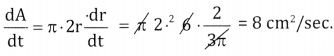
![]()
Question 5.
A circular patch of oil spreads on water the area growing at the rate of 16cm2/min. How fast are radius and the circumference increasing when the diameter is 12cm.
Answer:
Given \(\frac{\mathrm{dA}}{\mathrm{dt}}\) = 16cm2/min, d = 2r = 12cm, \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = ? \(\frac{\mathrm{dc}}{\mathrm{dt}}\) = ? r = 6cm
A = πr2 c = 2πr
\(\frac{\mathrm{dA}}{\mathrm{dt}}\) = π . 2r . \(\frac{\mathrm{dr}}{\mathrm{dt}}\) \(\frac{\mathrm{dc}}{\mathrm{dt}}\) = 2π \(\frac{\mathrm{dr}}{\mathrm{dt}}\)
16 = 2π .6 . \(\frac{\mathrm{dr}}{\mathrm{dt}}\) 2π . \(\frac{4}{3 \pi}=\frac{8}{3}\)cm / min
⇒ \(\frac{d r}{d t}=\frac{16}{12 \pi}=\frac{4}{3 \pi} \mathrm{cm} / \mathrm{min}\)
Question 6.
A stone is dropped into a pond waved in the form of circles are generated and the radius of the outer most ripple increases at the rate 2 inches/sec. How fast is the area increasing when the (a) radius is 5 inches (b) after 5 sec.?
Answer:
Given \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 2inch/sec, r = 5 inch, \(\frac{\mathrm{dA}}{\mathrm{dt}}\) = ?
(a) A = πr2
\(\frac{\mathrm{dA}}{\mathrm{dt}}\) = π2r. \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = π × 2 × 5 × 2 = 20π sq. inches / sec.
(b) After 5 sec, dr = 2dt
r = 2t
⇒ when t = 5, r = 10 inches
\(\frac{\mathrm{dA}}{\mathrm{dt}}\) = π . 2r \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = π × 2 × 20 × 2 = 40π square inches/sec.
Question 7.
The side of an equilateral triangle is increasing at the rate \(\sqrt{3}\) cm./sec. Find the rate at which its area is increasing when its side is 2 meters.
Answer:
Given \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = \(\sqrt{3}\) cm/sec., x = 2 meters, \(\frac{\mathrm{dA}}{\mathrm{dt}}\) = ?
Area of equilateral Δle = A = \(\frac{\sqrt{3}}{4}\) x2
\(\frac{d A}{d t}=\frac{\sqrt{3}}{4} \cdot 2 x \frac{d x}{d t}\)
= \(\frac{\sqrt{3}}{4}\) . 2. 200. \(\sqrt{3}\) = 300cm2 / sec.
Question 8.
Water is being poured at the rate of 30 mt3/min. into a cylindrical vessel whose base is a circle of radius 3 mt. Find the rate at which the level of water is rising?
Answer:
Given r = 3mts, \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 30 m3/min, \(\frac{\mathrm{dh}}{\mathrm{dt}}\) = ?
V = πr2h, r = constant
\(\frac{\mathrm{dv}}{\mathrm{dt}}\) = π . (3)2 . \(\frac{\mathrm{dh}}{\mathrm{dt}}\)
30 = 9π \(\frac{\mathrm{dh}}{\mathrm{dt}}\) ⇒ \(\frac{\mathrm{dh}}{\mathrm{dt}}\) = \(\frac{10}{3 \pi}\) meter/min.
![]()
Question 9.
Sand is being dropped at the rate of 10 mt3/sec. into a conical pile. If the height of the pile twice the radius of the base, at what rate is the height to the pile is increasing when the sand in the pile is 8mt high.
Given
\(\frac{d v}{d t}\) = 10m3/sec, h = 2r, h = 8, \(\frac{d h}{d t}\) = ?
r = \(\frac{\mathrm{h}}{2}\) \(\mathrm{v}=\frac{1}{3} \pi \mathrm{r}^{2} \mathrm{h}=\frac{1}{3} \pi \cdot\left(\frac{\mathrm{h}}{2}\right)^{2} \cdot \mathrm{h}=\frac{1}{3} \pi \frac{\mathrm{h}^{3}}{4}\)
\(\mathrm{v}=\frac{1}{12} \pi \mathrm{h}^{3} \Rightarrow \frac{\mathrm{dv}}{\mathrm{dt}}=\frac{\pi}{12} \cdot 3 \mathrm{h}^{2} \frac{\mathrm{dh}}{\mathrm{dt}} ; \quad 10=\frac{\pi}{4} \cdot 8^{2} \cdot \frac{\mathrm{dh}}{\mathrm{dt}}\)
\(\frac{d h}{d t}=\frac{40}{64 \pi}=\frac{5}{8 \pi} \mathrm{m} / \mathrm{sec}\)
Question 10.
A ladder of 15ft. long leans against a smooth vertical wall. If the top slides downwards at the rate of 2ft sec. Find how fast the lower and is moving when the lower end is 12ft. from the wall.
Answer:
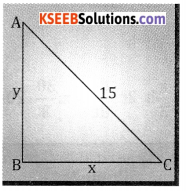
Given \(\frac{\mathrm{d} y}{\mathrm{dt}}\) = 2ft /sec, x = 12
From fig, x2 + y2 = 152
122 + y2 = 152
y2 = 152 – 122
y = \(\sqrt{225-144}\)
y = \(\sqrt{81}\) = 9
x2 + y2 = 152 ⇒ 2x \(\frac{\mathrm{dx}}{\mathrm{dt}}\) + 2y\(\frac{\mathrm{dy}}{\mathrm{dt}}\) = 0; 2.12.\(\frac{\mathrm{dx}}{\mathrm{dt}}\) + 2 .9 . 2 = 0
⇒ \(\frac{d x}{d t}=\frac{-36}{24}=\frac{-3}{2} f t / \sec\)
Question 11.
An edge of a variable cube is increasing at the rate of 10cm/sec. How fast the volume and also its surface area is increasing when the edge is 5cm long.
Answer:
Given \(\frac{d x}{d t}\) = 10 cm/sec, x = 5 cm, \(\frac{d v}{d t}\) = ? \(\frac{d s}{d t}\) = ?
(i) V = x3
\(\frac{d v}{d t}\) = 3x2 \(\frac{d x}{d t}\) = 3 × (52) × 10 = 750 cm3/sec.
(ii) S = 6x2 .
\(\frac{d s}{d t}\) = 12 × .\(\frac{d x}{d t}\) = 12.5 .10 = 600 cm2/sec.
![]()
Question 12.
A man 6ft. tall is moving directly away from a lamp post of height 10ft. above the ground. If he is moving at the rate 3ft./sec. Find the rate at which the length of his shadow is increasing and also the tip of his shadow is moving?
Answer:
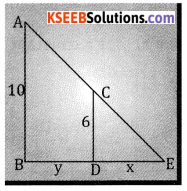
Let the shadow be x & y be the distance the man walks
Given \(\frac{d y}{d t}\) = 3ft/sec From a similar Δles we have
\(\frac{6}{10}=\frac{x}{x+y}\)
6x + 6y = 10x
6y = 4x ⇒ 3y = 2x
⇒ \(3 \frac{d y}{d t}=2 \frac{d x}{d t} \Rightarrow 2 \frac{d x}{d t}=3.3=9\)
∴ the shadow is increasing at the rate.
∴ \(\frac{d x}{d t}=\frac{9}{2}\) ft/sec & the tip of the shadow moves is
\(\frac{d x}{d t}+\frac{d y}{d t}=\frac{9+6}{2}=\frac{15}{2} \mathrm{ft} / \mathrm{sec}\)
Question 13.
The height of circular cone is 30 cm. and it is constant. The radius of the base is increasing at the rate of 0.25cm/sec. Find the rate of increase of volume of the cone when the radius of base is 10cm.
Answer:
dr
Given h = 30 cm, \(\frac{d r}{d t}\) = 0.25cm/sec. r = 10cm. dt
V = \(\frac { 1 }{ 3 }\) πr2h
\(\frac{d v}{d t}\) = \(\frac{\pi}{3}\)h.2r. \(\frac{d r}{d t}\) = π. \(\frac { 30 }{ 3 }\) . 20.(0.25) = 50π cm2 / sec
Question 14.
The volume of a spherical ball in increasing at the rate 4πcc/sec. Find the rate of increase of the radius of the ball when the volume is 288πCC.
Answer:
Given V = 288π C.C., \(\frac{d v}{d t}\) = 4πcc/ sec \(\frac{d r}{d t}\) = ?
V = \(\frac { 4 }{ 3 }\) πr3
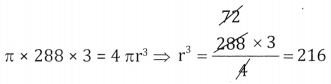
r = 6cm
\(\frac{d v}{d t}=\frac{4}{3} \pi \cdot 3 r^{2} \frac{d r}{d t} 4 \pi=\frac{4}{3} \pi \times 3 \times 36 \times \frac{d r}{d t} \Rightarrow \frac{d r}{d t}=\frac{1}{36} \mathrm{cm} / \mathrm{sec}\)
Question 15.
A drop of ink spreads over a blotting paper so that the circumferences of the blot is 4πcm and it changes 3cm/sec. Find the rate of increase of its radius and also find the rate of increase of its area?
Answer:
Given c = 4π, \(\frac{d C}{d t}\) = 3cm / sec \(\frac{d A}{d t}\) = ? \(\frac{d r}{d t}\) = ?
Circumference = c = 2πr
4π = 2πr ⇒ r = 2
Again
C = 2πr & A = πr2
\(\frac{d c}{d t}\) = 2π . \(\frac{d r}{d t}\) \(\frac{d A}{d t}\) = π . 2r. \(\frac{d r}{d t}\)
3 = 2π . \(\frac{d r}{d t}\) = π . 2. 2. \(\frac{3}{2 \pi}\)
⇒ \(\frac{d r}{d t}\) = \(\frac{3}{2 \pi}\) cm/ sec \(\frac{d A}{d t}\) = 6cm2 / sec
Question 16.
A circular plate of metal is heated so that its radius increase at the rate of O.lmm/min. At what rate is the [plate’s area increasing when the radius is 25cm [1cm = 10mm].
Answer:
Given \(\frac{d r}{d t}\) = 0.1 mm/min, r = 25 cm, \(\frac{d A}{d t}\) A = πr2
\(\frac{d A}{d t}\) = π. 2r . \(\frac{d r}{d t}\) = π . 2. /250 (0.1) = 50πmm2 /min.
![]()
Question 17.
The surface area of a spherical soap bubble increasing at the rate of 0.6cm2/sec. Find the rate at which its volume is increasing when its radius is 3cm.
Answer:
Given \(\frac{ds}{d t}\) = 0.6 cm2 / sec, r = 3cm, \(\frac{d v}{d t}\) = ?
s = 4 πr2 &
\(\frac{d s}{d t}\) = 4π. 2r. \(\frac{d r}{d t}\)
0.6 = 4π × 3 × 3 × \(\frac{d r}{d t}\)
∴ \(\frac{d r}{d t}=\frac{0.6}{6 \times 4 \pi}=\frac{0.1}{4 \pi} \mathrm{cm} / \mathrm{sec}\)
\(\frac { 1 }{ 40 }\) πcm/sec.
v = \(\frac { 4 }{ 3 }\) πr3
\(\frac{d v}{d t}=\frac{4}{3} \pi \cdot 3 r^{2} \frac{d r}{d t}\)
= 4πr2 \(\frac{d r}{d t}\)
= 4π(3)2 . \(\frac{0.1}{4 \pi}\)
= 0.9 cm3 / sec.
Question 18.
A rod 13 feet long slides with it end A and B as two straight lines at right angles which meet at ‘O’. If A is moved away from O with a uniform speed at 4ft./sec., find the speed of the end B move when A is 5 feet from O.
Answer:
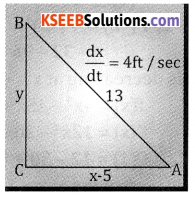
From fig we have
x2 + y2 = 132
y2 = 132 – 152 = 144
y = \(\sqrt{144}\) = 12
Als0
x2 + y2 = 132 ⇒ 2x \(\frac{d x}{d t}\) + 2y\(\frac{d y}{d t}\) = 0
\(5 \times 4=-12 \frac{\mathrm{dy}}{\mathrm{dt}} \Rightarrow \frac{\mathrm{dy}}{\mathrm{dt}}=-\frac{20}{12}=\frac{-5}{3}=\frac{\mathrm{dy}}{\mathrm{dt}}=\frac{-5}{3} \mathrm{ft.} / \mathrm{sec}\)
Question 19.
A street lamp is hung 12 feet above a straight horizontal floor on which a man of 5 feet is walking how fast his shadow lengthening when he is walking away from the lamp post at the rate of 175ft./min.
Answer:
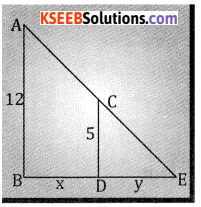
Let the shadow be y & the distance from the man walks is x.
Given \(\frac{d x}{d t}\) = 175 ft/min.
From figure we have
\(\frac{12}{5}=\frac{x+y}{y}\) ⇒ 12y = 5x + 5y ⇒ 7y = 5x
⇒ \(\frac{7 \mathrm{dy}}{\mathrm{dt}}=5 \frac{\mathrm{dx}}{\mathrm{dt}}\)
∴ the shadow is lengthening ⇒ \(\frac{d y}{d t}=\frac{5}{7} \times 175\) = 125 ft/ min.
Question 20.
Find a point on the parabola y2 = 4x at which the ordinate increases at twice the rate of the abscissa [Ordinate = y, abscissa = x].
Answer:
Given y2 = 4x diff. w.r.t. x
2y \(\frac{d y}{d x}\) = 4 \(\frac{d x}{d t}\)
Also given \(\frac{d y}{d x}\) = 2. \(\frac{d x}{d t}\) ⇒ 2y .2 \(\frac{d x}{d t}\) = 4. \(\frac{d x}{d t}\)
⇒ y = 1 ⇒ 12 = 4x
⇒ x = \(\frac { 1 }{ 4 }\)
∴ the point on the parabola is (\(\frac { 1 }{ 4 }\), 1 ).
![]()