Students can Download Basic Maths Exercise 19.3 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 19 Application of Derivatives Ex 19.3
Part- A
2nd PUC Basic Maths Application of Derivatives Ex 19.3 Two or Three Marks Questions with Answers.
Question 1.
Find the maximum and minimum value of the following function.
(i) f(x) = x3 – 3x
(ii) f(x) = x3 – 6x2 + 9x + 15(0 ≤ x ≤ 6)
(iii) f(x) = x4 – 62x2 + 120x + 9
(iv) f(x) = 2x3 – 3x2 – 12x + 12
(v) f(x) = 2x3 – 3x2 – 36x + 10
(vi) f(x) = 9x2 + 12x + 2
(vii) f(x) = 2x3 – 15x2 + 36x + 10
(viii) f(x) = 2x3 – 21x2 + 36x – 20
(ix) f(x) = 2x3 – 15x2 + 36x + 10
(x) f(x) = 12x5 – 45x4 + 40x3 + 6
Answer:
(i) Given f(x) = x3 – 3x …..(1)
f'(x) = 3x2 – 3 = 3(x2 – 1) = 3(x – 1) (x + 1) …..(2)
f'(x) = 0 ⇒ x = ±1
f”(x) = 6x – (3)
At x = 1, f”(1) = 6 > 0, f(x) is minimum at x = 1
& minimum value is f(1) = 1 – 3 = -2
At x = -1, f”(-1) = -6 < 0 f(x) is maximum at x = -1
Maximum value is f(-1) = -1 + 3 = 2
![]()
(ii) f(x) = x3 – 6x2 + 9x + 15 (0 ≤ x ≤ 6) – (1)
f'(x) = 3x2 – 12x + 9
= 3(x2 – 4x + 3) = 3 (x – 3) (x + 1] = 0
f “(x) = 6x – 12
f'(x) = 0 ⇒ x = 1 or 3
At x = 1 f”(1) = 6 – 12 = -6 < 0 the function is maximum at x = 1.
And maximum value is f (1) = 1 – 6 + 9 + 15 = 19
At x = 3, f”(3) = 6 × 3 – 12 = 18 -12 = 6 > 0, f is minimum at x = 3
And minimum value is f(3) = 33 – 6.32 + 9.3 + 15 = 27 – 54 + 27 + 15 = 15.
(iii) Given f(x) = x4 – 62x2 + 120x + 9 …..(1)
f”(x) = 4x3 – 124x + 120 ….(2)
f”(x) = 12x2 – 124 …..(3)
for a function to be maximum or minimum of f'(x) = 0.
⇒ x3 – 31x + 30 = 0 here x = 1 is a root
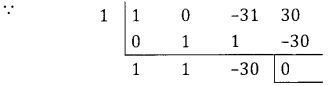
⇒ x2 + x – 30 = 0 ⇒ (x + 6)(x – 5) = 0 ⇒ x = 5 – 6
Put x = 1 in (3] we get f”(x) = (12 – 124) < 0
f(x) att-ains maximum at = 1 & maximum at x = 1 & max value is
f(1) = 1 – 62 + 120 + 9 = 68.
At x = 5, f”(5) = 12(5)2 124 = 300 – 124 > 0 f(x) attains
minimum at x = 5, & minimum value is f(5) = 625 – 1550 + 600 + 9 = – 316
At x = – 6, f “(-6) = 12 (-6)2 – 124 = 432 – 124 > 0
f(x) attains minimum at x = -6 & minimum value is
f (-6) = (-6)4 – 62(-6)2 + 120 (-6) + 9
= 1296 – 2232 – 720 + 9 = -1647.
(iv) f(x) = 2x3 – 3x2 – 12x + 12 ….(1)
f'(x) = 6x2 – 6x – 12 = 6 (x2 – x – 2) …(2)
f'(x) = 12x – 6 ….(3)
for a function to be maximum or minimum f ‘(x) = 0 ⇒ (x – 2) (x + 1) = 0
⇒ x = 2 or – 1
Put x = (-1) in (3) we get f “(-1) = -12 – 6 = -18 < 0
f(x) att-ains maximum at x = -1 & maximum value is
f(-1) = 2 (-1)3 – 3 (-1)2 – 12(-1) + 12 = 19
Put x = 2 in(3) f”(2) = 24 – 6 = 18 > 0
f(x) attains minimum at x = 2 & minimum value is
f(2) = 2 (2)3 – 3(2)2 – 12(2) + 12 = 6- ^-24+ >^=8
![]()
![]()
(v) Given f(x) = 2x3 – 3x2 – 36x + 10 ….(1)
f ‘(x) = 6x2 – 6x – 36 = 6 (x2 – x – 6) …..(2)
f “(x) = 12x – 6 ……(3)
For a function to be maximum of minimum f ‘(x) = 0
⇒ (x2 – x – 6) = 0 => (x – 3) (x + 2) = 0
⇒ x = 3 or – 2
Put x = 3 in equation (3) we get
f “(3) = 36 – 6 = 30 >0
⇒ f(x) attains minimum at x = 3
Minimum value is f(3) = 2(3)3 – 3 (32) – 36 (3) + 10
f(3) = 54 – 27 – 108 + 10 = -71
Put x = -2 in equation (3) we get
f”(-2) = -24 – 6 = – 30 < 0 ⇒ f (x) attains maximum at x = -2
Maximum value is f(-2) = 2(-2)3 -3(-2)2 – 36 (-2] + 10
f(-2) -16-12 + 72 + 10 = 54
(vi) Given f(x) = 9x2 + 12x + 2 ….(1)
f'(x) = 18x + 12 …(2)
f”(x) = 18 > 0 ……(3)
⇒ f(x) attains minimum
f'(x) = 0 ⇒ 18x+ 12 = 0 ⇒ x = \(-\frac{2}{3}\)
& f” \(\left(-\frac{2}{3}\right)\) 18 > 0 ⇒ f(x) is minimum & the minimum value is
f\(\left(-\frac{2}{3}\right)\) = 9\(\left(\frac{4}{9}\right)\) + 12 \(\left(-\frac{2}{3}\right)\) + 2
= 4 – 8 + 2 = -2
(vii) f(x) = 2x3 – 15x2 + 36x + 10 …….(1)
f ‘(x) = 6x2 – 30x + 36 = 6 (x2 – 5x + 6) ……..(2)
f”(x) = 12x – 30 …..(3)
f'(x) = 0 ⇒ x2 -5x + 6 = 0 ⇒ (x – 3)(x – 2) = 0 ⇒ x = 3 or 2
when x = 3 f “(x) = 12x – 30
f “(3) = 36 – 30 = 6 > 0 ⇒ f(x) has minimum
Minimum value is f(3) = 2(3)3 – 15(3)2 + 36(3) + 10
f(3) = 54 – 135 + 108 + 10 = 37
when x = 2, f”(2) = 24 – 30 = -6 < 0 ⇒ f(x) has maximum
maximum value is f(2) = 2(2)3 – 15(2) + 36(2) + 10
f(2) = 16 – 60 + 72 + 10 = 38.
![]()
(viii) Given f(x) = 2x3 – 21x2 + 36x – 20 ….. (1)
f'(x) = 6x2 – 42x + 36 …… (2)
= 6(x2 – 7x + 6)
f'(x) = 6 (x – 1) (x – 6) = 0 ⇒ x = 1 or 6
f”(x) = 12x – 42 … (3)
when x = l,f “(1) = 12 – 42 = -30 < 0 ⇒ f(x) is maximum
maximum value is f(1) = 2 – 21 + 36 – 20 = -3
when x = 6, f “(6) = 72 – 42 = 30 > 0 ⇒ f(x) is minimum
minimum value is f(6) = 2(6)33 – 21 (6)2 + 36(6) – 20
f(6) = 432 – 756 + 216 – 20 = -128
(ix) Given f(x) = 12x5 – 45x4 + 40 x3 + 6 ….(1)
f'(x) = 60x4 – 180x3 + 120x2 ….(2)
= 60x2 (x2 – 3x + 2)
= 60x2 (x – 1) (x – 2)
f ‘(x) = 0 ⇒ 60x2 (x – 1) (x – 2) = 0 ⇒ x = 0, 1, 2
f “(x) = 60 (4x3 – 6x + 4x) ……. (3)
when x = 0, f”(x) = 0 ⇒ f(x) has neither maximum nor minimum
when x = 1, f”(x) = -1 < 0 ⇒ f(x) has a maximum & maximum value is
f(1) = 12 – 45 + 40 + 6 = 13
When x =2 f”(x) = 4 > 0 ∴ f(x) has a minimum
minimum value is f(2) = 12(32) – 45(16) + 40(8) + 6
f(2) = 384 – 720 + 320 + 6 = -10.
Question 2.
The sum of two natural numbers is 48. Find the numbers when their product is maximum.
Answer:
Let the two numbers be x & y.
Given x + y = 48 & product: = xy where y 48 – x.
Let p = xy = x (48 – x) = 48x – x2.
\(\frac{d p}{d x}\) = 48 – 2x
\(\frac{d p}{d x}\) = 0 ⇒ 48 – 2x = 0 x = 24
\(\frac{\mathrm{d}^{2} \mathrm{p}}{\mathrm{d} \mathrm{x}^{2}}\) = -2 < 0 ⇒ product is maximum
x = 24 ⇒ y = 48 – 24 = 24
⇒ the two numbers are 24, 24.
![]()
Question 3.
Find two positive numbers whose sum is 14 and the sum of whose square is minimum.
Answer:
Let the two numbers be x and y
Given x + y = 14 & S = x2 + y2 where y = 14 – x
∴ S = x2 + (14 – x)2 = x2 + 142 + x2 – 28x = 2x2 – 28x + 142
\(\frac{d s}{d x}\) = 4x – 28 → (1) \(\frac{d s}{d x}\) = 0 ⇒ 4x – 28 = 0 ⇒ x = 7
\(\frac{\mathrm{d}^{2} \mathrm{s}}{\mathrm{d} \mathrm{x}^{2}}\) = 4 > 0, sum is minimum.
∴ y = 14 – x = 14 – 7 = 7
∴ the two positive number are 7 & 7.
Question 4.
Find two positive numbers whose sum is 30 and the sum of their cubes is minimum.
Answer:
Let the two numbers be x & y.
Given x + y = 30 & S = x3 + y3 where y = 30 – x
S = x3 + (30 – x)3 = x3 + (30)3 – x3 – 2700x + 90x2
\(\frac{d s}{d x}\) = – 2700 + 180x
\(\frac{d s}{d x}\) = 0 ⇒ x = \(\frac{2700}{180}\) = 15
\(\frac{\mathrm{d}^{2} \mathrm{s}}{\mathrm{d} \mathrm{x}^{2}}\) = 180 > 0 ⇒ sum of cubes is minimum & y = 30 – 15 = 15
∴ two positive number are 15 & 15.
Question 5.
The product of two natural numbers is 64. Find the numbers is their sum is minimum
Answer:
Let the two numbers be x & y
Given xy = 64 ⇒ y = \(\frac{64}{x}\)
Let s = x + y = x + \(\frac{64}{x}\).
\(\frac{d s}{d x}\) = 1 – \(\frac{64}{x^{2}}, \frac{d s}{d x}\) = 0 ⇒ x2 = 64 ⇒ x = ±8
\(\frac{d^{2} s}{d x^{2}}=+\frac{128}{x^{3}}\)
When x = 8, \(\frac{d^{2} s}{d x^{2}}=\frac{128}{8^{3}}\) > 0 ⇒ s is minimum
When x = -8, \(\frac{d^{2} s}{d x^{2}}=\frac{128}{8^{3}}\) < 0 ⇒ s is maximum
The two numbers are 8 & 8.
![]()