Students can Download Basic Maths Exercise 2.1 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 2 Permutations and Combinations Ex 2.1
Part – A
2nd PUC Basic Maths Permutations and Combinations Ex 2.1 One Mark Questions and Answers
Question 1.
Find the value of
(a) 12P6
(b) 8P6
(c) 10P5
(d) 10P2
Answer:
(a) 12P6 = 12 × 11 × 10 × 9 = 11,880
(b) 8P6 = 8 × 7 × 6 x 5 × 4 × 3 = 20,160
(C) 10P5 = 10 × 9 × 8 × 7 × 6 = 30,240
(d) 10P2 = 10 × 9 = 90
Question 2.
In how many ways can 9 soldiers stand in a queue.
Answer:
9 Soldiers can stand in a queue in 9! ways.
Question 3.
How many different signals can be made by taking 3 different coloured flags at a time from 7 different coloured flags.
Answer:
Number of permutations = 7P3 = 7 × 6 × 5 = 210.
![]()
Question 4.
If 5Pr = 60 find the value of r.
Answer:
Given 5Pr = 60
5Pr = 5 × 4 × 3 = 60
∴ r = 3
Question 5.
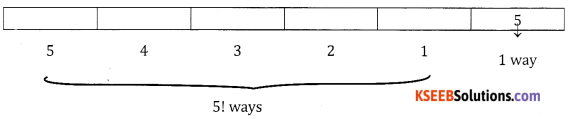
In how many ways can 5 letters be posted in 5 letter boxes if each box has one letter.
Answer:
5 letters can be posted in 5! ways = 120 ways.
Question 6.
How many different arrangements can be made with the letters of the word “MONDAY”.
Answer:
There are 6 letter in the word “Monday”. These 6 letters can be permuted in 6! ways = 720 ways.
Question 7.
How many six digit numbers can be formed with the digits 2, 7, 6, 1, 9, 8.
Answer:
Six digit numbers can be formed in 6! = 720 ways.
Question 8.
In how many ways can 4 people occupy 6 vacant chains.
Answer:
6 vacant chains can be occupied by 4 people in 6p4 ways = 6 × 5 × 4 × 3 = 360 ways.
Question 9.
There are 4 routes to go from A to B, and 3 routes to go from B to C. In how many ways can you go from A to C via B.
Answer:
The number of ways in which a person can go from A to B & B to C is 4 × 3 = 12 ways.
![]()
Question 10.
In how many ways can you go from A to B and return A from a different route, if there are 10 ways of travelling from A to B.
Answer:
The number of ways to travel from A to B is 10 ways. The number of ways to return from B to A in a different route is 9 ways.
∴ The total number of ways = 10 × 9 = 90 ways.
Part – B
2nd PUC Basic Maths Permutations and Combinations Ex 2.1 Two marks Questions and Answers
Question 1.
Find the value of n if nP5 = 20 nP3
Answer:
Given nP5 = 20 nP3
(n – 1) (n – 2) (n – 3) (n – 4) = 20 n(n – 1) (n – 2)
n – 3 = 5 ⇒ n = 8.
Question 2.
In how many ways can 7 persons be seated in a row if two persons always occupy the end seats.
Answer:
Two person always occupy the end seats they can be permuted in 2! ways & the remaining 5 can be permutted in 5! ways.
∴ The total number ways = 5! × 2! = 240 ways.
Question 3.
In how many ways can 3 boys and 4 girls be arranged in a row so that all the three boys are together.
Answer:
4 girls and 3 boys are together can be considered as 1 unit (total 5) can be permuted in 5! ways and 3 boys together can be permuted in 3! ways.
∴ Total number of ways = 5! 3! = 120 × 6 = 720 ways.
Question 4.
In how many ways the word “CARROM” be arranged such that the 2 R’s are always together.
Answer:
In the word “CARROM”, there are 6 letters, out of which 2 R’s are always together can be taken as 1 unit, can be permuted in 5! ways = 120 ways.
![]()
Question 5.
How many words can be formed from the letters of the word “FRIEND” which begin with Fand end with D.
Answer:
The word should begin with F and end with D, the remaining four can be permuted in 4! ways = 24 ways.
Question 6.
If nP3: nP2 = 3:1 find n.
Answer:

Question 7.
How many 4 digit numbers can be formed with the 0, 2, 3, 5, 7 such that no digits are repeated.
Answer:
First place can filled in 4 ways since 0 cannot in first place. The remaining places can be filled in 4, 3 and 2 ways respectively.

Total No. of ways = 4 × 4 × 3 × 2 = 96 ways.
Question 8.
How many 3 digit numbers ending with 7 can be formed using the digits 1, 2, 5, 7, 8 digits cannot be repeated.
Answer:
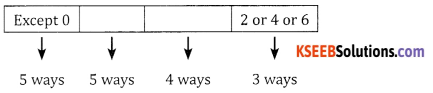
The number should end with 7, ∴ The units place can be filled by only one ways, the remaining 4 numbers can occupy the hundredth place in 4 ways and the tenth place in 3 ways.
∴ The total number of ways = 4 × 3 = 12 ways.
Question 9.
In how many ways can the letters of the word ‘HOPPER’ be arranged.
Answer:
In the word ‘HOPPER’, there are 6 letters out of which P is repeated twice.
∴ The number ways is \(\frac{6 !}{2 !}\) = 6 × 5 × 4 × 3 = 360 ways
Question 10.
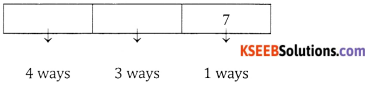
How many 6 digit numbers can be formed from the digits 1, 2, 3, 4, 5, 6 (no digit being repeated) which are divisible by 5.
Answer:
Since the number should be divisible by 5. The units place can be filled in only one way the remaining Five places can be filled in 5! ways = 120 ways.
![]()
Part – C
2nd PUC Basic Maths Permutations and Combinations Ex 2.1 Three Marks Questions and Answers
Question 1.
In how many ways can 7 students and 4 teachers be seated in a row such that no two teachers ar together.
Answer:
Since no two teachers are together and teachers must be seated in between students. 7 students can be permuted in 7! way, there are 8 places in which the 4 teachers can be seated in 8P4 ways.
∴ Total ways is 7! × 8P4
Question 2.
In how many ways can 7 books on art, 5 books on fiction, 4 books on adventure be arranged so that books of the same category are always together.
Answer:
The books of the same category should be together.
∴ 1 unit of art + 1 unit of fiction + 1 unit of adventure = 3 units can be permuted in 3! ways. 7 arts books can be permuted in 7! ways, 5 books on fiction can be permuted in 5! ways and 4 books on adventure can be done in 4! ways.
∴ Total number of ways is 3! × 7! × 5! × 4!.
Question 3.
5 men and 4 women are to be seated in a row so that women occupy the even places. How many 5 girls can be arranged in a row so that no two such arrangements are possible….
Answer:
Totally there are 9 people
m w m w m w m w m
There are four even places where 4 women can be seated in 4! ways. The 5 men be seated in the odd places in 5! ways.
∴ The total number of ways is 5! 4!
Question 4.
Find the number of ways in which 4 boys and 5 girls can be arranged in a row so thta no two boys are together and no two girls are together.
Answer:
No two boys and no two girls are together means the boys & girls must sit alternately. Four boys can be permuted in 4! ways & the 5 girls in 5! ways.
∴ The total number of ways is 5! × 4! ways.
![]()
Question 5.
Find the number of permutations of the letters of the word “MATHEMATICS”.
Answer:
Total letters = 11
m = 2 times, A = 2 times and T = 2 times.
∴ The total number of permutations = \(\frac{11 !}{2 ! \times 2 ! \times 2 !}\)
Question 6.
A family of 4 brothers and 3 sisters is to be arranged for a photograph in one row. In how many ways can they be seated if
(i) all the sisters sit together
(ii) No two sisters sit together.
Answer:
(i) All the sisters sit together can be taken as 1 unit the 4 brothers & 1 unit of sister can be seated in 5! ways for each of the sisters, who are together can be done in 3! ways.
∴ The number of ways = 5! 3!.
(ii) No two sisters are to others i.e., the sisters sit between the brothers _B_B_B_B_
There are 5 places in between the brothers which the 3 sisters can occupy is 5P3, ways and the brothers they themselves can permute in 4! ways.
∴ The number of ways is = 4! × 5P3 ways.
Question 7.
A code word is to consist of two distinct english alphabets followed by 2 distinct numbers between 1 and 9. How many such codes are possible.
Answer:
There are 26 alphabets, the first two places can be filled in 26 and 25 ways then 9 digits can be filled in 9 ways and the units place in 8 ways.
![]()
∴ The total number of ways = 26 × 25 × 9 × 8 = 46,800 ways.
![]()
Question 8.
When a group photograph is taken all the 10 teachers should be in the first row with principal and vice principal in the middle. The 18 students will be in second row with the two leaders at the extreme. How many arrangements are possible.
Answer:
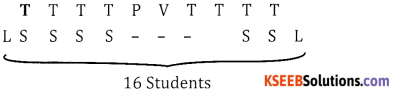
The principal and the vice principal can be seated in 2! ways, 8 teachers can be seated in 8! ways.
16 students can seated in 16! ways and 2 leaders can be seated in 2! ways.
∴ Total number of ways = 2! 8!16! 2! ways.
Question 9.
How many 5 digit even numbers can be formed using the digits 0, 1, 2, 3, 4, 5.
Answer:
(i) Without repitation
Case 1: If 0 is in units place remaining 4 places can be done in 5! ways = 120 ways.

Case 2:
If 0 is not in units place, the units place can be filled with 2 or 4 in two ways. The 1st place cannot be filled with 0, ∴ it can be filled in 4 ways similarly the remaining places can be filled in 4, 3, 2 ways respectively.
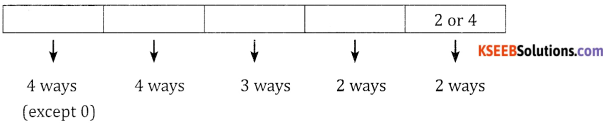
∴ Number of ways = 4 × 4 × 3 × 2 × 2 = 192 ways.
∴ Total number of ways = 120 + 192 = 312 ways.
(ii) With Repitation
Case 1: If 0 is filled in units place then the number of ways = 5 × 6 × 6 × 6 × 1 = 1,080 ways.

Case 2: If 0 is not filled in units place then the number of ways
= 5 × 6 × 6 × 6 × 2 = 10 × 216 = 2,160.

Total number of ways = 1,080 + 2,160 = 3,240.
Question 10.
How many numbers between 300 and 3,000 can be formed with the digits 0, 1, 2, 3, 4, 5.
Answer:
3 Digit Numbers: The hundredth place can be filled in 3 ways since the no. must be greater than 300; and the tens place can be filled in 5 ways and units place can be filled in 4 ways.
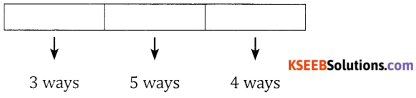
∴ The number of ways = 3 × 5 × 4 = 60 ways.
4 digit numbers: Less than 3,000 can be formed in = 2 × 5 × 4 × 3 = 120 ways.

∴ Total number of ways = 120 + 60 = 180 ways.
![]()
Question 11.
In how many ways the letters of the word “ACCOUNTANCY” be arranged? In how many of them vowels are always together.
Answer:
∴ Total letters = 10, A = 2, C = 2, N = 2, T = 2.
Total number of permutations \(=\frac{10 !}{(2 !)^{4}}=2,26,800\)

Vowels are together can be taken as 1 unit. Here letters can be permuted in \(\frac{7 !}{(2 !)^{3}}\) permuted in ways for each of these the four vowels can be permuted in \(\frac{4 !}{2 !}\)
∴ The number of ways is \(\frac{7 !}{(2 !)^{3}} \cdot \frac{4 !}{2 !}=630 \times 12=7,560\)
Part-D
2nd PUC Basic Maths Permutations and Combinations Ex 2.1 Five Marks Question and Answers.
Question 1.
Find the number of permutations of the letters of the word MISSISSIPPI. In how many of these
(a) the 4s’s are together
(b) the 4s’s are not together
(c) begin with MISS
(d) begin with SIP
Answer:
Total letters = 11, I = 4, S = 4, P = 2.
∴ The total number of permutations 7
4s’s are together can be taken as 1 unit i.e.

∴ The number of permutations = \(\frac{8 !}{4 ! \times 2 !}\) (b)
4s’s are not together = Total number of ways – 4s’s are together = \(\frac{11 !}{4 ! \times 4 ! \times 2 !}-\frac{8 !}{4 ! \times 2 !}\) (c)
Begin with MISS: The remaining 7 letters can be arranged in \(\frac{7 !}{3 ! \times(2 !)^{2}}\) (d)
Begin with SIP: The remaining 8 letters (I = 3, S = 3) can be arranged in \(\frac{8 !}{(3 !)^{2}}\)
Question 2.
Find the number of permutations of the letters of the “COMMITTEE”.
(a) How many of them begin with T and end with T.
(b) In how many all the vowels are together.
(c) In how many no two vowels are together.
(d) In how many of them end with MITE.
Answer:
Total letters = 9, M = 2, T = 2, E = 2
Total number of permutations \(\frac{9 !}{(2 !)^{3}}\)
(a) Number of permutations which being in with T and end with T is given by \(\frac{7 !}{(2 !)^{2}}\)
(b) Vowels are together can be taken as 1 unit.
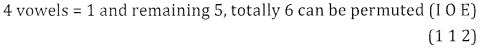
in \(\frac{6 !}{(2 !)^{2}}\) and the vowels they themselves can be done in \(\frac{4 !}{2 !}\) ways
∴ Total number of ways \(\frac{6 !}{(2 !)^{2}} \cdot \frac{4 !}{2 !}\)
(c) No two vowels are together: Should be in between the consonants, i.e. -C – M – M – T – T.
– There are 6 vacant places in between consonants to arrange 4 vowels. This can be arranged in \(\frac{^{6} \mathrm{P}_{4}}{2 !}\) and
5 consonants can be arranged in \(\frac{5 !}{(2 !)^{2}}\)
∴ Total number of ways = \(\frac{^{6} \mathrm{P}_{4}}{2 !} \times \frac{5 !}{(2 !)^{2}}\)
(d) End with MITE: The remaining 5 letters can be arranged in 5! ways.
![]()
Question 3.
Find the number of permutations of the letters of the word ASSASSINATION. In how many of these,
(a) The vowels are in odd places.
(b) Vowels are in odd places.
(c) The word NATION is always present together.
(d) Begins with ‘AS’ and ends with ‘AS’.
Answer:
Total Letters = 13, A = 3, S = 4, I = 2, N = 2, T = 1, 0 = 1.
This word can be arranged in = \(\frac{3 !}{3 ! \times 4 ! \times(2 !)^{2}}\)
(a) The vowels are in even places
The six vowels can be permuted in \(\frac{6 !}{3 ! \cdot 2 !}\)
There are 7 consonents, (S = 4, N = 2, T = 1), can be permutted in \(\frac{7 !}{4 ! \cdot 2 !}\)
The total number of ways = \(\frac{6 !}{3 ! \cdot 2 !} \cdot \frac{7 !}{4 ! \cdot 2 !}\)
(b) Vowels are in odd places: 1 2 3 4 5 6 7 8 9 10 11 12 13 14.
The 7 consonents can be placed in 7 even places in \(\frac{7 !}{4 ! \cdot 2 !}\) ways and 7 odd places in which the six vowels have to be placed in 7P6 ways for each of these 3 A’s and 21’s are repeated.
∴ Vowels can be permuted in \(\frac{7 p_{6}}{3 ! 2 !}\)
∴ Total number of ways = \(\frac{7 p_{6}}{3 ! \cdot 2 !} \times \frac{7 !}{4 ! \cdot 2 !}\)
(c) The word NATION is always present together: Can be taken as 1 unit and remaining is 7 totally 8 can be done in \(\frac{8 !}{2 ! \cdot 4 !}\)
(d) Begins with ‘AS’ and ends with ‘AS’: The remaining 9 letters (SSINATION) can be permuted in \(\frac{9 !}{2 ! \cdot 2 ! \cdot 2 !}\)
Question 4.
In how many ways can 7 English books, 8 Kannada books and 5 Hindi books be arranged in a shelf. In how many of these
(a) All Kannada books are together.
(b) No two English books are together.
(c) Books of the same language are together,
(d) All Kannada books are together and all Hindi books are together.
Answer:
7 English + 8 Kannda + 5 Hindi = 20 books can be permutted in 20! Ways.
(a) All Kannada books are together: Can be taken as 1 unit ∴ 1K + 71 + 5H = 13 books can be permutted in 13! Ways and 8 Kannada books, they themselves can be arranged in 8! Ways
∴ Total number of ways = 13!.8!
(b) No two English books are together: Can be arranged between the other books 8K + 5H = 13 books can be arranged in 13! ways there are 14 places between 13 books we have to arrange 17 English books can be done in 14p, ways
∴ The number of ways = 13!. 14P7
(c) Books of the same language are together: 1 unit of E + 1 unit of K + 1 unit of H = 3 units of books can be done in 3! Ways. 7 English, 8 Kannada and 5 Hindi books they themselves can be done in 7!, 8! and 5! Ways
∴ The total number of ways = 3! × 7! × 8! × 5!.
(d) All Kannada books are together and Hindi books are together: 1 unit of Kannada + 1 unit of Hindi + 7 English = 9 can be done in 9! ways and 8 Kannada books and 5 Hindi books, they themselves can be arranged in 8! and 5! Respectively.
∴ The total number of ways = 9! . 8! . 5!.
![]()
Question 5.
How many 4 digit numbers can be formed using digits 0, 1, 2, 3, 4, 5, 6 (No digit can be repeated) How many of them are:
(i) even
(ii) odd
(iii) greater than 4000
(iv) greater than 3,500.
Answer:
O cannot be filled in the Ist place, the number of ways = 6 × 6 × 5 × 4 = 720 ways

(i) Even
Case 1: 0 is filled in units place can be filled with 6 digits and remaining places can be filled in 5 and 4 ways respectively i..e, = 6 × 5 × 4 × 1 = 120 ways.

Case 2: If O is not in units place, as well as in Ist place there are 3 even numbers to be filled in units place. ist place in 5 ways and other two places by 5 and 4 ways respectively can be done in 5 × 5 × 4 × 3 = 300 ways
∴ Total even numbers are 120 + 300 = 420 ways

(ii) Odd: The number of odd numbers = Total – Even = 720 – 420 = 300.
(iii) Greater than 4000: The Ist place can be filled using the digits 5 (2 ways) or 6 and remaining places can be filled in 6,5 and 4 ways respectively.
∴ The number of ways = 3 × 6 × 5 × 4 = 360 ways

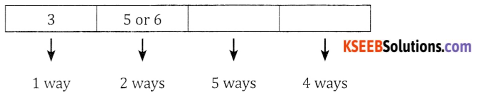
(iv) Greater than 3,500:
Case 1: 1st place can be filled by 4, or 5 or 6 in 3 ways and 2nd, 3rd and 4th places can be filled in 6 ways, 5 ways and 4 ways respectively.
∴ The number of ways = 3 × 6 × 5 × 4 = 360 ways

Case 2: If 3 is filled in the Ist place then the 2nd place can be filled using 5 or 6 (2 ways) and remaining places can be filled in 5and 4 ways respectively.
∴ The number of ways = 1 × 2 × 5 × 4 = 40 ways
∴ The total number of ways = 360 + 40 = 400 ways
![]()
Question 6.
How many 5 digit numbers can be formed using the digits 1, 2, 3, 5, 7, 9 (digits being repeated). How many of these are
(a) divisible by 5
(b) ending with 25
(c) less than 50,000
(d) greater than 75,000
Answer:
5 digit numbers without repetition = 7 × 6 × 5 × 4 × 3 = 2520.

(a) Divisible by 5: The units place can be filled by only one way (5) = 6 × 5 × 4 × 3 × 1 = 360 ways.

(b) Ending with 25: Tens place has to be filled using 2 and the units place using 5. This can be done in only one way 5 × 4 × 3 1 × 1 = 60 ways

(c) Less than 50,000: The 1st place can be filled by 4 ways (1 or 2 or 3 or 4)
∴ The number of ways = 4 × 6 × 5 × 4 × 3 = 1080 ways

(d) greater than 75,000:
Case 1: The Ist place is filled using digit 7 then the second place can be filled using 5,8 or 9 (3 ways), the remaining places can be filled in 5, 4 and 3 ways
∴ The number of ways is 3 × 5 × 4 × 3 = 180 ways
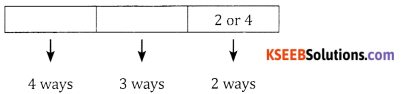
Case 2: The 1st place is filled using 8 or 9 (2 ways). The remaining can be filled using 6, 5, 4, 3 ways respectively
The number of ways = 2 × 6 × 5 × 4 × 3 = 720 ways.
∴ Total number of ways = 180 + 720 = 900 ways.
![]()
Question 7.
How many even numbers greater than 300 can be formed with the digits 1, 2, 3, 4, 5 no digit being a repeated. (Note: The numbers could be 3 digit, 4 digit or 5 digit].
Answer:
Case 1: 3 digit numbers: The units place can be filled using 2 or 4 (2 ways), the hundrenth place can be filled in 4 ways. Similarly the tens place can be filled in 3 ways.
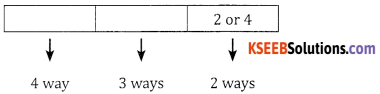
∴ The number of ways = 4 × 3 × 2 = 24 ways.
Case 2: 4 digit numbers.
Number of 4 digit numbers = 4 × 3 × 2 x 2 = 48 ways
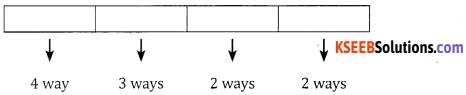
Case 3: 5 digit numbers.
Number of 5 digit numbers = 4 × 3 × 2 × 1 × 2 = 48 ways.
∴ Total number of even numbers greater than 300 = 24 +48 + 48 = 120 ways.

Question 8.
In how many ways can 6 boys and 6 girls be arranged in a row so that
(a) All girls are together.
(b) All boys are not together.
(c) No two girls are together.
(d) Boys and girls are arranged alternatively.
(e) Two particular girls are always together.
Answer:
(a) All girls are together: Consider 6 girls as one unit ∴ 6 boys + 1 unit of girls i.e., 7 members can be arranged in 7! Ways and 6 boys, they themselves can be arranged in 6! Ways.
∴ Total number of ways = 7! × 6!.
(b) All boys are not together: Total number of ways – Number of ways girls are together = 12! – 7! · 6!.
(c) No two girls are together: i.e., the girls must be between the boys, there are 7 places -B-B-B-B-B-B- in between the boys, 6 girls can be seated in 7P6 ways 6 boys they themselves can be arranged in 6! Ways.
∴ The number of ways = 7P6 . 6!
(d) Boys and girls are arranged alternatively: 6 boys and 6 girls are arranged alternatively BG BG BG BG BG BG in 6! × 6! Ways.
(e) Two particular girls are always together: Consider 2 girls are one unit, and they themselves can be arranged in 2! Ways, the remaining and girls, 6 boys and 2 girls together as 1 unit = (4 + 6 + 1 = 11) can be done in 11! Ways.
∴ The number of ways = 11! · 2!.
![]()
Question 9.
How many numbers can be formed with digits 2, 4, 6, 8 without repetition (Hint: numbers could be of 1 digit to 4 digits].
Answer:
Single digit only 4 numbers can be formed
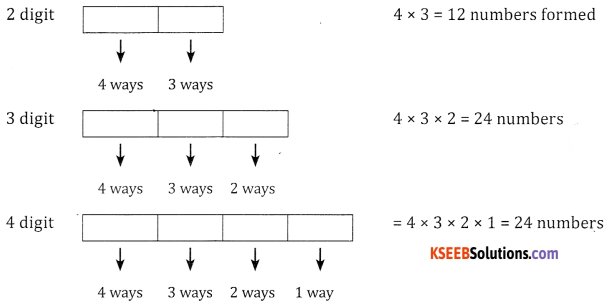
∴ Total numbers = 4 + 12 + 24 + 24 = 64 numbers.
Question 10.
How many four digit numbers can be formed using digits 0, 2, 3, 5, 7, 8.
(a) How many of them are even
(b) How many are divisible by 5
(c) How many are greater than 5300
(d) How many end with 7
[Hint: Here digits can be repeated]
Answer:
(a) Even numbers: The units place can be filled by 0,2 or 8 this can be done 3 ways
∴ The number of ways is 5 × 6 × 6 × 3 = 540 ways.
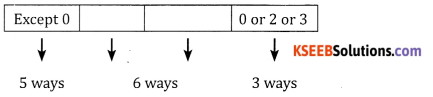
(b) Number divisible by 5: The units place can be filled by 0 or 5 in 2 ways ∴ the number of ways = 5 × 6 × 6 × 2 = 360 ways.
(c) greater than 5300:
Case 1: 5 is placed in thousands place. The 2nd place is done by (3 or 5 or 7 or 8) 4 ways
∴ the number of ways = 1 × 4 × 6 × 6 = 144 ways.
Case 2: If 7 or 8 is placed in thousandth place this can be done in 2 ways hundrenth place can be filled by any of the remaining six numbers
∴ The number of ways = 2 × 6 × 6 × 6 = 432 ways.
Hence the total number of ways is 432 + 144 = 576 ways.
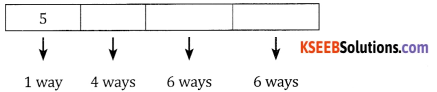
(d) End with 7: Units place can be filled only one way the 1st place can be filled by 5 ways ∴ the number of ways = 1 × 5 × 6 × 6 = 180 ways.
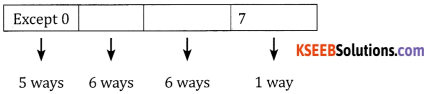
Question 11.
Find the number of permutations of the letters of the word UNIQUE
(a) How many of them end with QUE.
(b) How many begin with U and end with E.
(c) In how many vowels are in even places.
(d) In how many all vowels are together.
Answer:
There are six letters in which repeated twice can be permutted in \(\frac{6 !}{2 !}\) ways \(\frac{720}{2}\) = 360 ways
(a) The words end with QUE: The remaining 3 letters can be arranged in 3! Ways = 6 ways.
(b) The words begin with U and end with E: The remaining 4 letters can be permuted in 4! Ways = 24 ways.
(c) The four vowels can be placed in 3 even places in 4P3, ways and the remaining 3 can be permutted in 3! ways i.e.,\(\frac{4 \times 3 \times 2}{2}\) = 12 ways.
(d) All 4 vowels can be taken as 1 unit ∴ the total 1 + 2 = 3 can be done in 3! Ways and 4 vowels can be permuted in \(\frac{4 !}{2 !}\) =12 ways.
∴ The number of ways = 12 × 6 = 72 ways.
![]()
Question 12.
How many 4 digit even numbers can be formed using the digits 0, 1, 2, 3, 4, 5, 6
(a) when digits can be repeated
(b) when digits are not repeated
Answer:
(a) When digits can be repeated: The units place can be filled by the 4 even numbers in ways. For each of these the remaining places can be filled in 6, 7, 7 ways
∴ the numbers are 6 × 7 × 7 × 4 = 1176.
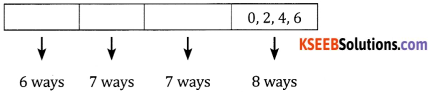
(b) When digits are not repeated:
Case 1: O is filled in units place thousandth place can be filled in 6 ways ∴ the number of ways = 6 × 5 × 4 × 1 = 120 ways.
Case 2: O is not filled in units place and not in thousandth place also :: the units place can be filled in 3 ways (2 or 4 or 6)
∴ The number of ways = 5 × 5 × 4 × 3 = 300 ways
∴ The total number of ways = 300 + 120 = 420 ways