Students can Download Basic Maths Exercise 20.3 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 20 Indefinite Integrals Ex 20.3
Part-A
2nd PUC Basic Maths Indefinite Integrals Ex 20.3 Two Marks Questions and Answers
Question 1.
\(\int \frac{3 x^{2}}{1+x^{3}} d x\)
Answer:
\(\int \frac{3 x^{2}}{1+x^{3}} d x\) = log(1 + x3)+c or using \(\int \frac{\mathrm{f}^{\prime}(\mathrm{x})}{\mathrm{f}(\mathrm{x})} \mathrm{d} \mathrm{x} = log (f(x) + c\)
put 1 + x3 = t
∴ 3x2dx = dt
∴ = ∫\(\frac { 1 }{ t }\)dt = log t + c = log(1 + x3) + c
Question 2.
\(\int \frac{4 x+3}{2 x^{2}+3 x+5} d x\)
Answer:
\(\int \frac{4 x+3}{2 x^{2}+3 x+5} d x\) = log(2x2 + 3x +5) + c
∴ \(\int \frac{\mathrm{f}^{\prime}(\mathrm{x})}{\mathrm{f}(\mathrm{x})} \mathrm{d} \mathrm{x}\) = log(f(x)) + C
Question 3.
\(\int \frac{e^{x}-1}{e^{x}-x} d x\)
Answer:
\(\int \frac{e^{x}-1}{e^{x}-x}\) = log(ex – x) + c
![]()
Question 4.
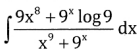
Answer:
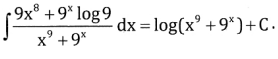
Question 5.
\(\int \frac{\cos x}{2+\sin x} d x\)
Answer:
\(\int \frac{\cos x}{2+\sin x} d x\) = log(2 + sin x) + c
Question 6.
\(\int \frac{1}{x(2 \log x+5)} d x\)
Answer:
\(\int \frac{1 / x^{d x}}{2 \log x+5}\)
\(\int \frac{d t / 2}{t}=\frac{1}{2} \int \frac{1}{t} d t\)
= \(\frac { 1 }{ 2 }\)log t + c
= \(\frac { 1 }{ 2 }\)log (2 log x + 5) + c
put 2 log x + 5 = t
2. \(\frac { 1 }{ x }\) dx = dt
\(\frac { 1 }{ x }\) dx = \(\frac { dt }{ 2 }\)
Question 7.
\(\int \frac{3 \sin x}{3+4 \cos x} d x\)
Answer:
\(\int \frac{3 \sin x}{3+4 \cos x} d x\)
\(=\int \frac{3 \cdot \frac{d t}{-4}}{t}=\frac{-3}{4} \int \frac{1}{t} d t\)
= \(\frac { -3 }{ 4 }\) log t + c
= \(\frac { -3 }{ 4 }\) log(3 + 4 cos x) + c
put 3 + 4 cos x = t
– 4 sinx dx = dt
sin x dx = \(\frac { dt }{ -4 }\)
![]()
Part-B
2nd PUC Basic Maths Indefinite Integrals Ex 20.3 Five Marks Questions and Answers
Question 1.
\(\int \frac{1}{\sqrt{x}+x} d x\)
Answer:

Question 2.
\(\int \frac{\sin 2 x}{1+\cos ^{2} x} d x\)
Answer:
\(\int \frac{\sin 2 x}{1+\cos ^{2} x} d x\)
= \(\int \frac{-d t}{t}\)
= -log t + c
= -log (1 + cos2x) + c
put 1 + cos2x = t
2 cosx (-sinx) dx = dt
-sin 2x dx = dt
sin 2x dx = -dt
Question 3.
\(\int \frac{e^{2 x}+1}{e^{2 x}-1} d x\)
Answer:
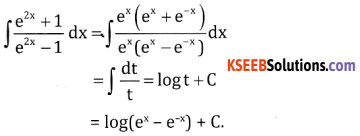
Question 4.
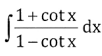
Answer:
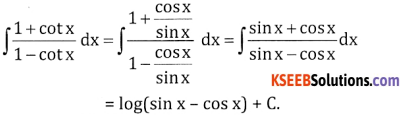
![]()
Question 5.
\(\int \frac{\cot x}{3+\log (\sin x)} d x\)
Answer:
\(\int \frac{\cot x}{3+\log (\sin x)} d x\)
\(=\int \frac{d t}{t}\)
= log t + c = log(3 + log(sin x)) + c
put 3 + log(sin x) = t
\(\frac{\cos x}{\sin x} d x=d t\)
cos x dx = dt
Question 6.
\(\int \frac{\csc ^{2} x \cdot \cot x}{4+5 \csc ^{2} x} d x\)
Answer:
\(\int \frac{\csc ^{2} x \cdot \cot x}{4+5 \csc ^{2} x} d x\)
\(=\int \frac{-1 / 10^{\mathrm{dt}}}{t}=\frac{-1}{10} \log t+C\)
= \(\frac { -1 }{ 10 }\)log(4 + 5cosec2x) + c
put 4 + 5 cosec2x = t
– 10 cosec x – cosec x × cot x dx = dt
cosec2x . cot dx = \(\frac { -1 }{ 10 }\)dt