2nd PUC Basic Maths Question Bank Chapter 21 Definite Integral and its Applications to Areas Ex 21.2

Students can Download Basic Maths Exercise 21.2 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Basic Maths Question Bank Chapter 21 Definite Integral and its Applications to Areas Ex 21.2

Part-A

Applications of Areas

2nd PUC Basic Maths Definite Integral and its Applications to Areas Ex 21.2 Two marks Questions and Answers

Question 1.
Find the area bounded by the curve y = x², x – axis and the ordinates x = 0, x = 1
Answer:

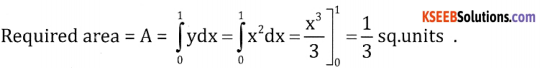
Question 2.
Find the area bounded by the curve y² = 8x, x – axis and the lines x = 0, x = 2
Answer:

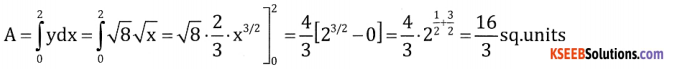
Question 3.
Find the area bounded by the curve x² = 8y, y-axis and the abscissas y = 3, y = 6
Answer:

Question 4.
Find the area bounded by the curve 3x² = 4y, y-axis and the lines y = 1, y = 2
Answer:

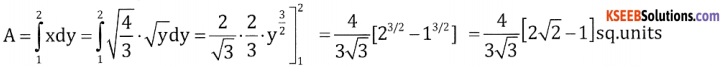
Part- B

2nd PUC Basic Maths Definite Integral and its Applications to Areas Ex 21.2 Five Marks Questions and Answers

Question 1.
Find the area bounded by the parabola y² = 4ax and its latus rectum.
Answer:

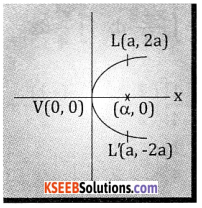
Question 2.
Find the area bounded by the parabola y² = 4x and x² = 4y
Answer:

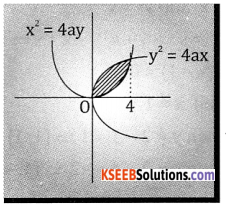
Given
y² = 4x and x²= 4y
\(\left(\frac{x^{2}}{4}\right)^{2}\) ∵y = \(\frac{x^{2}}{4}\)
\(\frac{x^{4}}{16} = 4 x\)
x⁴ – 4³x = 0
x(x³ – y³) = 0 ⇒ x = 0, x = 4

Question 3.
Find the area bounded by the curve y² = 5x and the line y = x
Answer:
y² = 5x and y = x
x² – 5x = 0
x(x – 5 ) = 0 ⇒ x = 0 and x = 5

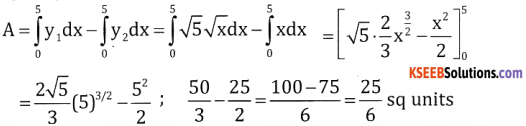
Question 4.
Find the area enclosed between the parabola x² = 4y and the line x = 4y – 2

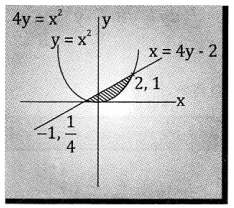
Answer:
Given x² = 4y and line x = 4y – 2
x = x² – 2 ∴ 4y = x²
x² – x – 2 = 0
(x – 2) (x + 1) = 0
⇒ x = 2, y = -l
So when x = 2, y = 1 ⇒ (2, 1)
When x = -1, y = \(\frac { 1 }{ 4 }\) ⇒ \(\left(-1, \frac{1}{4}\right)\)
These two points where line meets parabola as we got these values by solving the 2 equations,
So, required area

Question 5.
Find the area enclosed between the parabola y² = x and the line x + y = 2
Answer:
Given y = 2 – x and y² = x
⇒ [2 – x]² = x ⇒ 4 + x² – 4x = x ⇒ x² – 5x + 4 = 0
⇒ (x – 4) (x – 1) = 0
⇒ x = 4 and x = 1
when x = 1 then y = 2 – 1 = 1 ⇒ (1,1)
when x = 4 then y = 2 – 4 = -2 ⇒ (4, -2)

Question 6.
Find the area enclosed between the parabola y² = 4ax and the line y = mx
Answer:

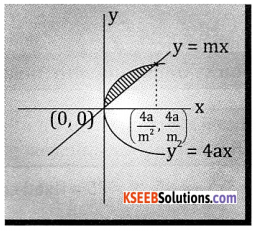
Given y² = 4ax and line y = mx.
Points where both meet at a \(\left(\frac{4 a}{m^{2}}, \frac{4 a}{m}\right)\) and (0,0)
⇒ y² = 4ax
m²x² = 4ax ⇒ x = \(\frac{4 \mathrm{a}}{\mathrm{m}^{2}}\) and y = mx = \(\mathrm{m} \cdot \frac{4 \mathrm{a}}{\mathrm{m}^{2}}=\frac{4 \mathrm{a}}{\mathrm{m}}\)
Required area = Area of y² = 4ax from 0 to \(\frac{4 \mathrm{a}}{\mathrm{m}^{2}}\) – Area of the line y = mx from 0 to \(\frac{4 \mathrm{a}}{\mathrm{m}^{2}}\)