Students can Download Basic Maths Exercise 4.2 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 4 Binomial Theorem Ex 4.2
Part – A
2nd PUC Basic Maths Binomial Theorem Ex 4.2 Two Marks Questions and Answers
1. Find
Question (i).
The 5th term in \(\left(\frac{4 x}{5}-\frac{5}{2 x}\right)^{8}\)
Answer:
\(\left(\frac{4 x}{5}-\frac{5}{2 x}\right)^{8}\) compare with (x + a)n
⇒ x → \(\frac{4 x}{5}\), a → \(\frac{4 x}{5}\) n → 8,
To find th term put r = 4
Tr+ = nCr.xn – r.ar
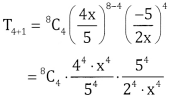
T5 = 8C4.(22).2-4
8C4.28-4 = 8C4.24 = 1120
Question (ii).
The 8th term in \(\left(\frac{a}{2}-\frac{3}{b}\right)^{10}\)
Answer:
\(\left(\frac{a}{2}-\frac{3}{b}\right)^{10}\) compare with (x+a)n
⇒ x → \(\frac{a}{5}\), a → \(\frac{2}{b}\) n = 10,
To find 8th term put r = 7
Tr+ = nCr.xn – r.ar
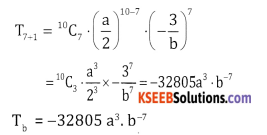
![]()
Question (iii).
The 6th term in (√x – √y)17
Answer:
Compare (√x – √y)17 with (x + a)n
x → √x a → -√y and n = 17
To find 6th term put r = 5
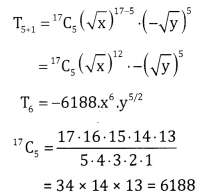
Question (iv).
The 7th term in (3x2 – \( \frac{y}{3}\) )9
Answer:
Here x → 3x2 a → \(-\frac{y}{3}\) nn = 9
Put r = 6
T6+1 =9C6 (3x2)9-6. ( \(-\frac{y}{3}\) )6
![]()
Question (v).
the 10th term in \(\left(\frac{a}{b}-\frac{2 b}{a^{2}}\right)^{12}\)
Answer:

Question (vi).
the 11th term in \(\left(x+\frac{1}{\sqrt{x}}\right)^{14}\)
Answer:
Here x = x a = \(\frac{1}{\sqrt{x}}\) ,n = 14 and
put r = 10
T10+1 = 14C10 .x14 – 10 . \(\left(\frac{1}{\sqrt{x}}\right)^{10}\) 14C4.x4 \(\frac{1}{x^{5}}\) = \(\frac{1001}{x}\)
![]()
Part – B
2nd PUC Basic Maths Binomial Theorem Ex 4.2 Three Marks Questions and Answers
Question 2.
Find the middele term in the expansion of
Question (i).
\(\left(x-\frac{1}{2 y}\right)^{10}\)
Answer:
\(\left(x-\frac{1}{2 y}\right)^{10}\)
Here n = even i.e 10 ∴ we have only one middle term \(\frac{\mathrm{n}}{2}+1=\frac{10}{2}+1\) = 6th term
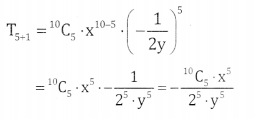
Question (ii).
\(\left(\frac{a}{x}+b x\right)^{12}\)
Answer:
\(\left(\frac{a}{x}+b x\right)^{12}\)
Here
n = 12 (even)
∴ We have only one middle term
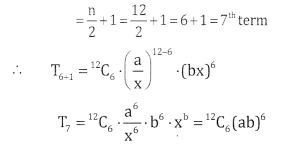
Question (iii).
\(\left(\frac{2 a}{3}-\frac{3}{3 a}\right)^{6}\)
Answer:
Here n = 6 (even)

Question (iv).
\(\left(3 x-\frac{1}{6} x^{3}\right)^{8}\)
Answer:

Question (v).
\(\left(\frac{a}{3}+\frac{b}{3}\right)^{8}\)
Answer:
Here n = 8(even)
∴ middle term \frac{\mathrm{n}}{2} + 1 = 4 + 1 = 5th
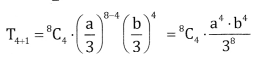
![]()
3. Find the middle terms in the expansion of
Question (i).
Find the middle term in the expansion of
\(\left(3 x-\frac{2}{x^{2}}\right)^{15}\)
Answer:
Here n = 15 and odd, so we have two middle terms i.e, \(\frac{n+1}{2}=\frac{15+1}{2}=8^{t h}\) and 8 + 1 = 9th terms to find 8 thterm to find 8 th term pur r = 7

Question (ii)
\(\left(\frac{x}{2}+\frac{3}{x^{2}}\right)^{19}\)
Answer:
Here n = 19 (odd)∴ We have two middle terms \(\frac{n+1}{2}=\frac{20}{2}\) 10th and 10 + 1 =11th term To find 10th term put r = 9

Question (iii)
\(\left(2 x^{2}+\frac{1}{\sqrt{x}}\right)^{11}\)
Answer:
Here n = 11 (odd)
∴ the two middle terms are \(\frac{13+1}{2}\) = 7th and 6 + 1 = 7th terms
To find 6th term put r = 5
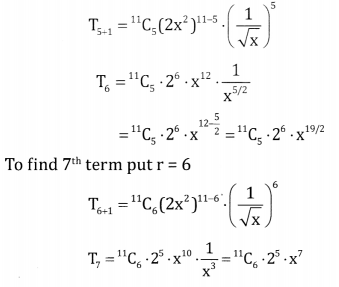
Question (iv).
\(\left(\sqrt{x}-\frac{4}{x^{2}}\right)^{11}\)
Answer:
Here n = 11(odd) we have two middle term
i.e, \( \frac{1+1}{2}\) = 6th and 6 + 1 = 7th terms
To find 6th term put r = 5.
![]()

Question (v).
\(\left(\sqrt{x}-\frac{3}{x^{2}}\right)^{13}\)
Answer:
\(\left(\sqrt{x}-\frac{3}{x^{2}}\right)^{13}\)
Here n = 13 (odd)
∴ the two middle terms are \(\frac{13+1}{2}\) = 7th and 7 + 1 = 8th terms
To find 7th term put r = 6

Part – C
2nd PUC Basic Maths Binomial Theorem Ex 4.2 Five Marks Questions and Answers
4.
Question (i).
Find the coefficent of xn in \(\left(x+\frac{2}{x^{2}}\right)^{17}\)
Answer:
Here x = x a = \(\frac{2}{x^{2}}\) and n = 17
Tr+1 = nCr . x n-r.ar
= 17Cr .x 17-r.( \(\frac{2}{x^{2}}\) )r = 17Cr . 2r.x 17-r-2r
= 17Cr 2 r.x 17-3r
To find coefficient of x11 equate the power of x to 11
⇒ 17 – 3r = 11 ⇒ 17 – 11 = 3r
⇒ 3r = 6 ⇒ r = 2
T2+1 = 17C2 . 22.x11
∴ Coefficient of x” is 17C2 .22 = \(\frac{17 \times 16 \times 2}{2 \times 1}\) = 544
Question (ii).
Y3 in \(\left(7 y^{2}-\frac{2}{y}\right)^{12}\)
Answer:
Here x =7y2, a = \(-\frac{2}{y}\) and n = 12
Tr+1 = 12Cr(7Y2)12-r.\(\left(\frac{-2}{y}\right)^{r}\)
= 12Cr.712-r .y24-2r. y-r(-2)r
Tr+1 = 12Cr.712-r.(-2)r.y24-3r
To find the coefficient of y3 equate the power of y ro 3
i.e., 24 – 3r = 3 ⇒ 21 = 3r ⇒ r= 7
∴T7+1 = 12C7 .712-7. (-2)7 y3
= -12C7 .75 27 . y3
∴Coefficient of y3 is -12C7.75.27
Question (iii).
x11 in \(\left(\sqrt{x}-\frac{2}{x}\right)^{17}\)
Answer:
lere, x → √x, a →\(\frac{-2}{x}\) and n = 17
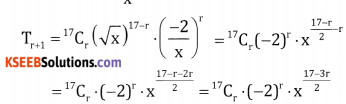
To find the coefficient of x2 equate the power of x to -11
∴ \(\frac{17-3 r}{2}\) = -11 ⇒ 17 – 3r = – 22
⇒ 17+22 = 3r ⇒ 39 = 3.r ⇒ r = 13
T13+1 = 17C13(-2)13.x-11
Coefficient of x-11 is -17C13.213
Question (iv).
X18 in \(\left(x^{2}-\frac{6}{x}\right)^{15}\)
lere, x → x2, a →\(\frac{-6}{x}\) and r = 15
Tr+1 = 15Cr.(x2)15-r\(\left(\frac{-6}{x}\right)^{r}\)
Tr+1 = 15Cr.x30-2r.(-6)r.x-r
= 15Cr.(-6)r.x30-2r-r
= 15Cr(-6)r.x30-3r.
To find the coefficient of x18,equate the power of x to 18
∴ 30 – 3r = 18 ⇒ 30 – 18 = 3r ⇒ 3r = 12 ⇒ r = 4
T4+1 = 15C4(-6) 4x18
∴ Coefficient of x18 is 15C4. (6)4
![]()
Question (v).
X-2 in \(\left(x+\frac{1}{x^{2}}\right)^{17}\)
Answer:
Here, x → x, a → \(\frac{1}{x^{2}}\) and n = 17
∴ Tr+1 = 17Cr.x17-r\(\left(\frac{1}{x^{2}}\right)^{r}\)
Tr+1 = 17Cr.x17-r-2r
= 17Crx17-3r
To find the coefficient of x-2,equate the power of x to -2
17 – 3r = -2 ⇒ 17 + 2 = 3r ⇒ 3r ⇒ r = \(\frac{19}{3}\)
Since r is a fraction the coefficient of x-2 is 0.
Question (vi).
X5 in \(\left(x+\frac{1}{x^{2}}\right)^{17}\)
Answer:
Here, x → x, a → \(\frac{1}{x^{2}}\) and n = 17
Tr+1 = 17Cr.x17-r\(\left(\frac{1}{x^{2}}\right)^{r}\)
= 17Crx17-3r
To find the coefficient of x5, equate the power of x to 5
∴ 17 – 3r = 5
12 = 23 ⇒ r = 4
T4+1 = T5 = 17C4.x5
∴ the coefficient of x5 is 17C4
Question (vii).
X18 in \(\left(x^{2}+\frac{3 a}{x}\right)^{15}\)
Answer:
Here x → x2 a → \(\frac{3 \mathrm{a}}{\mathrm{x}}\) , n=15
∴ Tr+1 = 15Cr.(x2)15-r \(\left(\frac{3 a}{x}\right)^{r}\)
= 15Crx30-2r.(3a)rxr
=15Cr .3r.ar.x30-3r
To find the coefficient of x18, we get 30 – 3r = 18
12 = 3r ⇒ r =4
∴ T4+1 = 15C4.34.a4.x18
∴ coefficient of x18 is 15C4.(3a)4
5. Find the term independent of x in
Question (i).
\(\left(\frac{4 x^{2}}{3}+\frac{3}{2 x}\right)^{9}\)
Here x → \(\frac{4 x^{2}}{3}\) , a = \(\frac{3}{2 x}\) and n = 9

To find the term independent of x, equate the power of x to zero.
e., 18 – 3r = 0 ⇒ r = 6
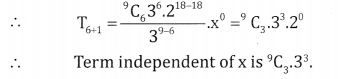
Question (ii).
\(\left(x^{3}-\frac{3}{x^{2}}\right)^{15}\)
Answer:
Here x → x3, a = \(\frac{-3}{x^{2}}\) and n = 15
Tr+1 = 15Cr.(x3)15-r.\(\left(\frac{-3}{x^{2}}\right)^{r}\)
= 15Cr.x45-r.x-2r (-3)r
= 15Cr.(-3)r.x45-5r
To find the term independent of x we have 45 – 5r = O
:. 45 = 5r ⇒ r = 9
T9+1 = 15C9.(-3)9.x0
T10 = -15C9.(3)9 is the term independent of x.
![]()
Question (iii).
\(\left(\sqrt{x}+\frac{1}{3 x^{2}}\right)^{10}\)
Answer:

Question (iv).
\(\left(\frac{3 x^{2}}{2}-\frac{1}{3 x}\right)^{9}\)
Answer:

Question (v).
\(\left(3 x-\frac{2}{x^{2}}\right)^{15}\)
Answer:
Here x → 3x a → \(\frac{-2}{x^{2}}\) and n =15
Tr+1 = 15Cr.(3x)15-r.\(\left(\frac{-2}{x^{2}}\right)^{r}\)
= 15Cr.315-r.(-2)r . x15-r
We have x15-3r. = x0 ⇒ 15 = 3r ⇒ r = 5
T = 15C5.315-5.(-2)5 = -15C5 .310 25
∴ The term independent of x is -15C5.310.25
Question (vi).
\(\left(x^{2}-\frac{2}{x^{3}}\right)^{5}\)
Answer:
Here x → x2 a → \(\frac{-2}{x^{3}}\) = 5r(x2)5 – r . \(\left(\frac{-2}{x^{3}}\right)^{r}\)= 5r.x10-2r.(-2)r
= 5Cr(-2)r.x10-5r
We have 10 – 5r = 0 ⇒ r = 2
T2+1 = T3 = 5C2(-2)2.x0 = 4. \(\frac { 5.4}{ 2.1 }\) = 40
∴ The term independent of x is 40
Question (vii).
\(\left(x-\frac{1}{x^{2}}\right)^{21}\)
Answer:
Here x →x and a → \(\frac{-1}{x^{2}}\) and n= 21
Tr+1 = 21Cr.(x)21-r. \(\left(\frac{-1}{x^{2}}\right)^{r}\)
= 21Cr.x21-3r.(-1)r
We have x0= x21-3r ⇒21 = 3r ⇒ r = 7
∴ T7+1 = T8 = 21C7 (-1)7.x0 = -21C7
∴ The term independent of x is -21C7
Question (viii).
\(\left( \sqrt { 2 } \frac { 2 }{ { x }^{ 2 } } \right)\)<sup>20</sup>
Answer:

Part – D
2nd PUC Basic Maths Binomial Theorem Ex 4.2 Four Marks Questions and Answers
6. Use binomial theorem to evaluate upt 4 decimals place
Questoin (i)
(102)6
(102)6 = (100 + 2)6
= (100)6 + 6C1(1 0O)5. 2 + 6C2(100)4.22 + 6C3(100)3.23 + 6C4(100)2 24 + 6C5.100.25 + 6C626
= 1000000000000 + 120000000000 + 6000000000 + 160000000 + 2400000 + 19200 + 64
= 1,126,162,419,264
Question (ii).
(98)4
Answer:
(98)4 = (100 – 2 )4
= (100) 4– 4C1 (100)3.2 + 4C2(100)2.22 – 4C3(100).23 + 4C4.24
= 100000000 – 8000000 + 240000 – 3200 + 16
= 92236816
![]()
Question (iii).
(1.0005)4
Answer:
(1.0005)4 = (1 + 0.0005)4
= 14 + 4C1(O.0005) + 4C2(0.0005)2 + 4C3(0.0005)3 + 4C4(0.0005)4
1 + 0.002 + 0.0000015 + …………….
= 1.00200150 ≈ 1.0020
Question (iv).
(0.99)4
Answer:
(0.99)4 = (1- 0.01)4 = 4C0(0.01) – 4C1 (0.01) + 4C2(0.O1)2 – 4C3(0.01)3 + 4C4(0.01)4
= 1 – 0.04 + 0.0006 – 0.000004 + 0.00000001
= 0.96059601 ≈ 0.9606
Question 7.
The first three terms in (1 + ax)n where n is a positive integer are 1, 6x, 16x2. Find the vaIue
Answer:
Given . T1 = lin (1 + ax)n; T2 = 6x
nC1 .ax = 6x
nax = 6x
⇒ na = 6 ⇒ a = \(\frac{6}{n}\)
and T3 = 16x2
\(\frac{n(n-1)}{2}\) a2x2 = 16x2
Question 8.
In the expansion of (3 + kx)9 the x2 and x3 are equal. Find k.
Answer:
Given , Tr+1= 9Cr.39-r.(kx) r
= 9Cr.39-r.krxr
Coefficient of x2 ⇒ x2 ⇒ r = 2
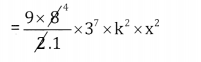
36x 37.k2 x x2
Coefficient of x3 ⇒ x3 = xr⇒ r = 3

T3+1 = T4 = 93.39-3.k3.x3 = 9C3.36
k3.x3 = 84.36k3.x3
84 x 36k2= 36 x 37 x k2
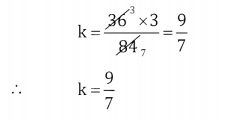
![]()
Question 9.
Find the ratio of the coefficient of x4 in the two expansions (1+x)7 and (1+x)10?
Answer:
