2nd PUC Basic Maths Question Bank Chapter 5 Partial Fractions Ex 5.2

Students can Download Basic Maths Exercise 5.2 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Basic Maths Question Bank Chapter 5 Partial Fractions Ex 5.2

Part – A

2nd PUC Basic Maths Partial Fractions Ex 5.2 Five Marks Questions and Answers

I. Resolve the following into partial fractions; (3 and 5 marks)

Question 1.
\(\frac{x}{(x+1)(x-4)}\)
Answer:

Put
x = 4, 4 = A(0) +B (4 + 1) ⇒ 4 = 5B ⇒ B = \(\frac{4}{5}\)
Put x = -1, -1 = A(-1-4) +B(0) ⇒ -1 = -5A = A=\(\frac{1}{5}\)
Substituting both A & B in equation (1) we get

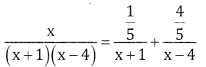
Question 2.
\(\frac{x+1}{(x+2)(x-3)}\)
Answer:
\(\frac{x+1}{(x+2)(x-3)} =\frac{A}{x+2}+\frac{B}{x-3}\)………………….. (1)
x = 3, 3 + 1 = A(0) +B(3 + 2)
4 = 5B = B = \(\frac{4}{5}\)
Put
x = -2, -2 + 1 = A(-2 – 3) + B(0)
-1 = A(-5)
A = 1/5;
3 = -A ⇒ A = -3

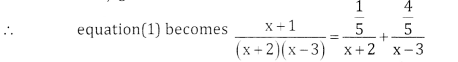
Question 3.
\(\frac{7 x-1}{(1-2 x)(1-3 x)}\)
Answer:
Let
\(\frac{7 x-1}{(1-2 x)(1-3 x)}=\frac{A}{1-2 x}+\frac{B}{1-3 x}\)
⇒ (7x – 1) = A(1 – 3x) + B(1 – 2x)
Put x = 0, -1 = A + B …………..1
Put x=1 6 = -2A-B …………………….2
Solving 1 & 2 (adding) -A = 5 ⇒ A = -5
B = -1-A = -1 + 5 = 4.

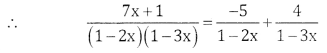
Question 4.
\(\frac{3-7 x^{2}}{(1-3 x)(1+2 x)(1+x)}\)
Answer:
Let
\(\frac{3-7 x^{2}}{(1-3 x)(1+2 x)(1+x)}=\frac{A}{(1-3 x)}+\frac{B}{1+2 x}+\frac{C}{1+x}\) …………… (1)
∴ 3 – 7x² = A(1 + 2x) (1+x) +B(1 – 3x) (1 + x) +C (1 – 3x) (1 + 2x)
Put x = -1, 3 – 7 = A(0) + B(0) +C(1 +3) (1-2)
-4 = -4C ⇒ C = 1
Put x = 0, 3 = A + B + C = A + B = 2
Put x = 1, 3 – 7 = A(1 + 2) (1 + 1) + B(1 – 3) (1 + 1) +C(1 – 3) (1 + 2)
-4 = 6A – 4B – 6C ∵ C= 1
-4 + 6 = 6A – 4B = 2
3A – 2B = 1 2A + 2B = 4
⇒ A + B=2

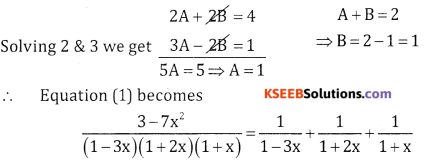
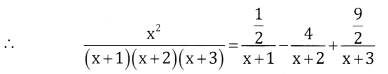
Question 5.
\(\frac{x^{2}}{(x+1)(x+2)(x+3)}\)
Answer:
Let \(\frac{x^{2}}{(x+1)(x+2)(x+3)}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{x+3}\)
x² = A(x +2) (x + 3) +B(x + 1) (x + 3) + C(x + 1) (x + 2)
Put x=-1, (-1)² = A(-1 +2) (-1 + 3) + 0 + 0
1 = 2A ⇒ A =\(\frac{1}{2}\)
Put x = -2, (-2)² = A(0) + B(-2 + 1) (-2 + 3) + C(0)
4 = -B ⇒ b = -4
Put x = -3, (-3)² = A(0) + B(0) +C(-3 + 1) (-3 + 2)
9 = -2C:(-1) ⇒ 9 = 2c ⇒ c = \(\frac{9}{2}\)
Equation 1 be becomes

Question 6.
Answer:
\(\frac{2 x^{2}+10 x-3}{(x+1)(x-3)(x+3)}\)
Let

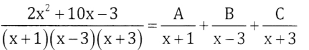
2x² +10x – 3 = A[x – 3) (x + 3) + B(x + 1) (x + 3) + C(x +1) (x – 3)
Put x=-1, 2 – 10 – 3 = A(-4) (2) + B(0) + C(0)
-11 = -8A = A = \(\frac{11}{8}\)
Put x = 3, 18 + 30 – 3 = A(0) + B(4)(6) + C(0)
+45 = 24B ⇒ B = \(\frac{45}{24}=\frac{15}{8}\)
Put x = -3, 18 – 30 – 3 = C(-3 + 1) (-3 -3) = C(-2) (-6)-15 = + 12C
C = \(\frac{-15}{12}=\frac{-5}{4}\)

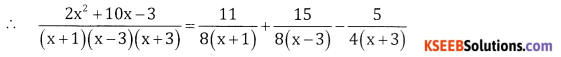
Question 7.
\(\frac{3 x+1}{x^{2}-6 x+8}\)
Answer:

Question 8.
\(\frac{x^{2}-10 x+13}{(x+1)\left(x^{2}-5 x+6\right)}\)
Answer:
Let

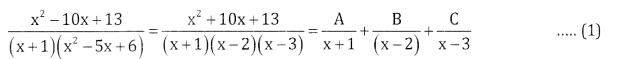
x² – 10x + 13 = A(x-2)(x – 3) + B(x +1) (x – 3) + C(x + 1) (x – 2)
Put x=-1, 1 + 10 + 13 = A (-3) (-4) + 0 + 0
24 = 12A ⇒ A = \(\frac{24}{12}\)=2
Put x = 2, 4 – 20 + 13 A(0) + B(3) (-1) + C(0)
-3 = -3B ⇒ B = 1
Put x = 3, 9 – 30 + 13 = A(0) + B(0) + C(4) (1)
-8 = 47 ⇒ C= -2

Question 9.
\(\frac{3 x+20}{x^{2}+4 x}\)
Answer:
Let \(\frac{3 x+20}{x^{2}+4 x}=\frac{3 x+20}{x(x+4)}=\frac{A}{x}+\frac{B}{x+4}\) ……..(1)
3x + 20 = A(x + 4) + B(x)
Put x=0, 20 = 4A ⇒ A = 5
Put x = -4, -12 + 20 = A(0) + B(-4)
8 = -4B ⇒ B = -2
\(\frac{3 x+20}{x^{2}+4 x}=\frac{5}{x}-\frac{2}{x+4}\)

Question 10.
\(\frac{x+3}{(x-1)\left(x^{2}-4\right)}\)
Answer:
Let \(\frac{x+3}{(x-1)\left(x^{2}-4\right)}=\frac{x+3}{(x-1)(x-2)(x+2)}=\frac{A}{x-1}+\frac{B}{x-2}+\frac{C}{x+2}\) ……(1)
(x + 3) = A[x -2) (x + 2) +B(x – 1) (x + 2) + C(x – 1) (x – 2)
Put x= 1, 4 = A(-1)(3) ⇒ A=\(\frac{-4}{3}\)
Put x = 2, 5 = A(0) + B(1) (4) + C(O)
Put 5 = 4B ⇒ B = \(\frac{-4}{3}\)
Put x = -2, -2 + 3 = A(0) + B(0) +C(-3) (-4)
1 = 12C ⇒ C = \(\frac{1}{12}\)

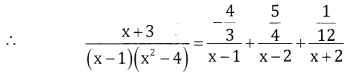
Question 11.
\(\frac{x+3}{x^{3}-x}\)
Answer:
Let \(\frac{x+3}{x^{3}-x}=\frac{x+3}{x(x-1)(x+1)}=\frac{A}{x}+\frac{B}{x-1}+\frac{C}{x+1}\) ….. (1)
x + 3 = A(x-1) (x + 1) + B(x) (x + 1) + C(x) (x – 1)
Put x = 0 3 = -A + 0 + 0 ⇒ A=-3
Put x = 1, 4 = A(0) + B(1) (2) + 0 = 4 = 2B ⇒ B = 2
Put x = -1, 2 = A(0) + B(0) + C(-1) (-2); 2 = 2c ⇒ c = 1
∴ \(\frac{x-3}{x^{3}-x}=\frac{-3}{x}+\frac{2}{x-1}+\frac{1}{x+1}\)

Question 12.
\(\frac{1+3 x+2 x^{2}}{(1-2 x)\left(1-x^{2}\right)}\)
Answer:
Let


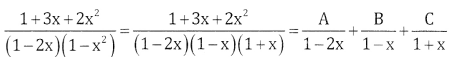
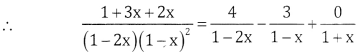
1 + 3x + 2x² = A(1 – x)(1 + x) +B(1 – 2x)(1 + x) + C(1 – 2x) (1 – x)
Put x = 1, 6 = A(0) + B(-1)(2) +C(0);
6 = -2B ⇒ B = -3
Put x=-1, 0) = A(0) + B(0) +C(1 + 2)(2)
6C = 0 ⇒ C = 0
Put x = 0, 1 = A + B + C = A – 3 = 1 ⇒ A = 1 + 3 = 4

Part – B

1. Resolve the following into partial fractions; (5 Marks)

Question 1.
\(\frac{4}{(x-3)(x+1)^{2}}\)
Answer:
Let \(\frac{4}{(x-3)(x+1)^{2}}=\frac{A}{x-3}+\frac{B}{x+1}+\frac{C}{(x+1)^{2}}\)
∴4 = A(x + 1)² + B(x + 1)(x – 3) + C(x – 3)
Put x = 3, 4 = A(4)² + B(0) + C(0)
4 = 16A ⇒ A = \(\frac{1}{4}\)
Put x =-1, 4 = A(0) + B(0) + C(-1-3); Put 4 = -4C ⇒ C = -1
Put x = 0 4 = A- 3B – 3C
3B = A – 3C – 4

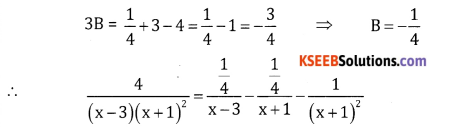
Question 2.
\(\frac{9}{(x+1)(x+2)^{2}}\)
Answer:
Let \(\frac{9}{(x+1)(x+2)^{2}}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2)^{2}}\)
9 = A(x + 2)² + B(x + 1)(x + 2) +C(x + 1)
Put x = -1, 9 = A(-1 + 2)² + 0 + 0
A = 9
Put x= -2, 9 = A(0) + B(0) + CC – 10 = -9
Put x = 0, 9 = 4A + 2B + C
9 = 36 + 2B -9
9 = 27 + 2B \(\frac{-18}{2}\) = B B = -9
∴ \(\frac{9}{x-1}-\frac{9}{x+2}-\frac{9}{(x+1)^{2}}\)

Question 3.
\(\frac{3 x+4}{(x+1)^{2}(x-1)}\)
Answer:
Let \(\frac{3 x+4}{(x+1)^{2}(x-1)}=\frac{A}{x+1}+\frac{B}{(x+1)^{2}}+\frac{C}{x-1}\)
3x+4 = A(x + 1)(x – 1) + B(x – 1) + C (x + 1)²
Put x = -1, ⇒ 3 + 4 = A(0) + B(-2) + C(0)
1 = -2B ⇒ B = \(-\frac{1}{2}\)
Put x = 1, = 3 + 4 = A(0) +B(0) + C(2)²
7 = 4C ⇒ C = 5
Comparing the coefficients of x² on both sides
0 = A +C ⇒ A = -C = \(-\frac{7}{4}\)

Question 4.
\(\frac{3 x+2}{(x-2)(x+3)^{2}}\)
Answer:
Let \(\frac{3 x+2}{(x-2)(x+3)^{2}}=\frac{A}{x-2}+\frac{B}{x+3}+\frac{C}{(x+3)^{2}}\)
(3x + 2) = A(x + 3)² + B(x – 2) (x + 3) + C(x – 2)
Put x = 2, 6 + 2 = A(2 + 3)² + B(0)+C (0)
8 = 25A ⇒ A = \(\frac{8}{25}\)
Put X=-3, -9 + 2 = A(0) + B(0) +C(-5)
-7 = -5C ⇒ C = \(\frac{7}{5}\)
Comparing the co-efficients of x2 on both sides
0 = A + B ⇒ B = -A = \(\frac{8}{25}\)

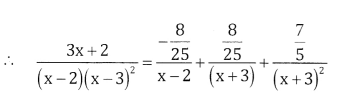
Question 5.
\(\frac{2 x^{2}-4 x+1}{(x+2)(x-3)^{2}}\)
Answer:
2x² – 4x + 1 = A[x – 3)² + B(x – 2) (x-3) + C (x – 2)
Put x = 2, 8-8 + 1 = A(-1)² = A = 1
Put x = 3, 18 – 12 + 1 = A(0) + B(0) + C(3 – 2) = 7 = C
Comparing coefficient of x² = 2 = A + B = B = 2-A = 2 -1 =1
∴ \(\frac{2 x^{2}-4 x+1}{(x-2)(x-3)^{2}}=\frac{1}{x-2}+\frac{1}{x-3}+\frac{7}{(x-3)^{2}}\)

Question 6.
\(\frac{x^{2}}{(x+1)^{2}(x-5)}\)
Answer:
Let \(\frac{x^{2}}{(x+1)^{2}(x-5)}=\frac{A}{x+1}+\frac{B}{(x+1)^{2}}+\frac{C}{x-5}\)
x² = A (x + 1)(x – 5) + B(x – 5) + C(x + 1)²
Put x = -1, 1 = A(0) + B(-1-5) + C(0)
1 = -6B ⇒ B = \(-\frac{1}{6}\)
Put x = 5, 25 = A(0) + B(0) + C(6)²
C = \(\frac{25}{36}\)
Compare the coefficients of x2 on both sides we get

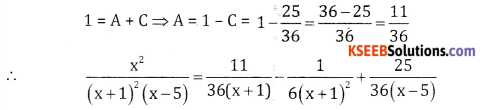
Question 7.
\(\frac{4-7 x}{(2+3 x)(1+x)^{2}}\)
Answer:
Let \(\frac{4-7 x}{(2+3 x)(1+x)^{2}}=\frac{A}{2+3 x}+\frac{B}{1+x}+\frac{C}{(1+x)^{2}}\)
⇒ 4 – 7x = A(1 + x)² +B(1 + x) (2 + 3x) + C(2 + 3x)
Put x=-1, 11 = A(0) + B(0) + C(-1)
C = -11
Put x = 0 4 = A + 2B + 2C ⇒ 26 = A + 2B …..(1)
Compare the coefficients off of x² on both sides
0 = A + 3B …….(2)
Equations 1 – 2 gives 26 =-B = 0 ⇒B = -26& A = 78
∴ \(\frac{4-7 x}{(2+3 x)(1+x)^{2}}=\frac{78}{2+3 x}-\frac{26}{1+x}-\frac{11}{(1+x)^{2}}\)

Question 8.
\(\frac{1+2 x}{(x+2)^{2}(x-1)}\)
Answer:
Let \(\frac{1+2 x}{(x+2)^{2}(x-1)}=\frac{A}{x+2}+\frac{B}{(x+2)^{2}}+\frac{C}{x-1}\)
1 + 2x = A (x + 2) (x – 1) + B(x – 1) +C(x + 2)²
3 = A(0) + B(0) + C(9) ⇒ C = \(\frac{1}{3}\)
Put x = -2, 1 – 4 = B(-3) ⇒ B = 1
Comparing the coefficient of x² on both sides we get

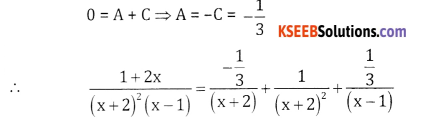
Question 9.
\(\frac{9 x-27}{(2+1)(x-2)^{2}}\)
Answer:
Let \(\frac{9 x-27}{(2+1)(x-2)^{2}}=\frac{A}{x+1}+\frac{B}{x-2}+\frac{C}{(x-2)^{2}}\)
9x – 27 = A(x – 2)² + B(x + 1)(x – 2) + C(x + 1)
Put x = -1, -36 = A(-3)² + B(0) + C(0)
-36 = 9A ⇒ A=-4
Put x = 2, 18 – 27 = A(0) + B(0) +C(2+1)
-9 = 3C ⇒ C =-3
Comparing the coefficients of x? on both sides
0 = A + B = B = -A ⇒ B =-(-4) = 4

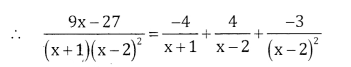
Question 10.
\(\frac{2 x+5}{(x+2)(x-1)^{2}}\)
Answer:
Let \(\frac{2 x+5}{(x+2)(x-1)^{2}}=\frac{A}{x+2}+\frac{B}{x-1}+\frac{C}{(x-1)^{2}}\)
2x + 5 = A(x – 1)² + B(x – 1)(x + 2) +C(x + 2)
Put x = -2, -4 + 5 = A(-3)² + 0 + 0
1 = 9A ⇒ A =\(\frac{1}{9}\)
Put x= 1, 2 + 5 = A(0) + B(0) + C(1 + 2)
7 = 3C ⇒ C = \(\frac{7}{3}\)
Comparing the coeff of x2 on both sides
0 = A+B ⇒ B = A = \(-\frac{1}{9}\)

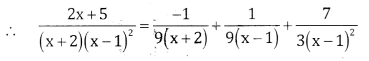
Question 11.
\(\frac{x}{(1+2 x)^{2}(1-3 x)}\)
Answer:
Let \(\frac{x}{(1+2 x)^{2}(1-3 x)}=\frac{A}{1+2 x}+\frac{B}{(1+2 x)^{2}}+\frac{C}{1-3 x}\)
X = A(1 + 2x) (1 – 3x) + B(1 – 3x) + C(1 + 2x)2
Put x = 0 we get A + B + C = 0
Comparing co efficient of x2 both sides
0 = -6A + 40 ⇒ 6A = 4C ⇒3A = 20
We have A+B+C = 0
⇒ 3A + 3B + 3C = 0
2C + 3B + 3C = 0
5C = -3B
: 3A = 2C
Comparing the coefficient of x both sides

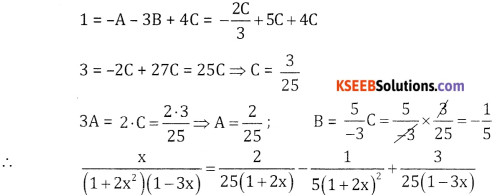
Part – C

III. Resolve into partial fractions: (5 Marks)

Question 1.
\(\frac{2 x^{2}-7 x+1}{x^{2}-3 x-4}\)
Answer:
\(\frac{2 x^{2}-7 x+1}{x^{2}-3 x-4}\)
This is an improper fraction
∴ Convert into proper fraction by actual division.

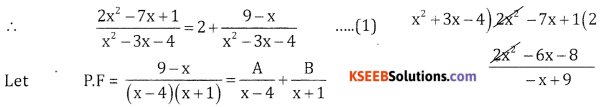
9- x = A(x + 1) + B(x – 4)
Put x = 4, 9-4 = A(4 + 1) + B(0)
5 = 5A ⇒ A = 1
Put x=-1, 9-(-1) = A(0) +B(-1-4)
10 = -5B ⇒ B = -2

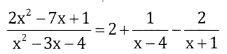
Question 2.
\(\frac{4 x^{2}-3 x+5}{(2-x)(1+x)}\)
Answer:

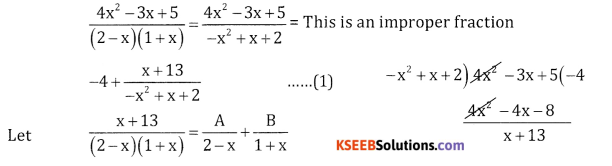
x + 13 = A(1 + x) + B(2 – x)
Put x = 2, 15 = A[1 + 2) + B(0)
15 = 3A ⇒ A = \(\frac{15}{3}\) = 5
Put x=-1, -1 + 13 = A(0) +B(2-(-1))
12 = 3B ⇒ B = 4

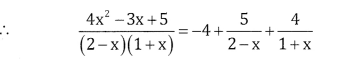
Question 3.
\(\frac{x^{3}+7 x^{2}+17 x+11}{x^{2}+5 x+6}\)
Answer:

(x – 1) = A(x + 3) + B(x + 2)
Put x = -2, -3 = A(-2 + 3) + B(0)
-3 = A ⇒ A=-3
Put X=-3, -4 = A(0) + B(-3 + 2)
-4 = -B ⇒ B = 4

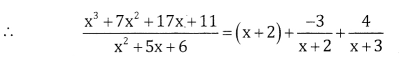
Question 4.
\(\frac{2 x^{2}+3 x+2}{x^{2}-x-2}\)
Answer:

∴ 5x + 6 = A (x + 1) +B(x – 2)
Put x = 2, 16 = A(3) ⇒ A = \(\frac{16}{3}\)
Put x = -1, 1 = A(0) + B(-3)=B = \(\frac{1}{-3}\)
1 2x+3x+2-21 16 1 x – x – 2 =2+3(x-2) 3(x+1)

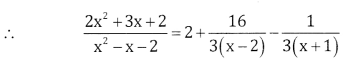
Question 5.
\(\frac{2 x^{3}+x^{2}-x-3}{x(x-1)(2 x+3)}\)
Answer:

∴ 2x – 3 = A[x -1) (2x + 3) +B(x) (2x + 3) + C(x) (x – 1)
Put x = 0 -3 = A(-1) (3) + B(0) + C(0)
-3 = -3A ⇒ A = 1
Put x = 1, -1 = A(0) + B(1) (2 + 3) + C(0)
-1 = 5B ⇒ B = \(-\frac{1}{5}\)
Compare the co-efficient of x² both sides