2nd PUC Basic Maths Question Bank Chapter 6 Mathematical Logic Ex 6.2

Students can Download Basic Maths Exercise 6.2 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Basic Maths Question Bank Chapter 6 Mathematical Logic Ex 6.2

Part – A

2nd PUC Basic Maths Mathematical Logic Ex 6.2 One Mark Questions and Answers

Question 1.
Negate the following propositions.
(1) p ∨ ~ q
(ii) ~p → q
(iii) ~p ∧ ~q
(iv) p ∧ ~q
(v) ~p → ~q
Answers:
(i) ~ (p ∨~q)  ≡ ~p ∧~(~9) = ~p ∧ q ( ∵ ~(~q) = q )
(ii) ~(~p → q) ≡ ~p ∧ ~q
(iii) ~(~p ∧~q) ≡ ~(~p) ∨~(~q) = p ∨ q   (∵ ~(~p) = p)
(iv) ~ (p ∧ ~q) ≡ ~p ∨~(~q) = ~p ∨ q
(v) ~(~p →~q) ≡~p ∧~(~q) =~p ∧ q.

Question 2.
Negate the following.
(i) 4 is an even integer or 7 is a prime number.
(ii) He likes to run and he does not like to sit.
(iii) He likes Mathematics and he does not like Logic.
(iv) If 6 is a divisor of 120 then 486 is not dividiable by 6.
(v) If 2 triangles are similar then their ares are equal.
(vi) It is cold or it is raining,
Answers:
(i) Let p: 4 is even integer, q: 7 is a prime number given (p v q)
~(p ∨ q) = ~ p ∧ ~q
4 is not an even integer & 7 is not a prime number

(ii) Let p: He likes to run, q: He likes to sit
Given is ~ p ∧ ~q
∴ ~ (p ∧~ ) = ~p ∨ ~(~q) ≡ ~p ∨ q
He does not like to run or he likes to sit

(iii) Let p: He likes mathematices, q: He like logic
Given (p ∧ ~q)
~ (p ∧ ~q) ≡ ~p ∨ q
He does not like mathematics or he likes logic

(iv) Let p: 6 is a divisor or 120
q: 486 is divisible by 6
Given (p → ~ q)
~(p → ~ q) = p ∧ ~(~q)

(v) Let p: 2 triangles are similar.
q: Areas are equal
Given (p → q)
∴ ~(p → q) = (p ∧ ~q)
2 triangles are similar & areas are not equal.

(vi) p: It is cold
q: It is raining Given p ∨ a
~(p ∨ q) =~p∧~q
It is not cold & it is not raining

Part B

2nd PUC Basic Maths Mathematical Logic Ex 6.2 Two Marks Questions and Answers

Question 1.
Negate
(i) p → (q ∧ r)
(ii) q ∨ [~(p ∧ r)] |
(iii) (p → q)∧( q → p/q)
(iv) p→ (q ∧ ~r)
Answers:
(i) ~ [p → (p ∧ r)] = p ∧~(q ∧ r) ≡ p ∧ (~q ∨ ~r)
(ii) ~ [q ∨ (~ (p ∧ r)] ≡ ~q ∧ ~[~ (p ∧ r) ≡ ~q ∧ (p ∧ r)
(iii) ~[(p →q) ∧ (q → p)] ≡ ~ (p →q) ∨ ~(q → p)
≡ (p ∧ ~q) ∨ (q ∧ ~p)
(iv) ~[p → (q^~r)] = p ∧ ~(q ∧ ~r)
= p ∧ [(-q ∨ ~(~r)]
= p ∧(~q ∨ r)

Question 2.
Negate the following:
(1) If an integer is greater than 3 and less than 5 then it is a multiple of 5.
(ii) If ‘x’ is divisible by ‘y’ then it is divisible by ‘a’ and ‘b.
(iii) Weather is fine and my friends are not coming or we do not go to a movie.
(iv) If a triangle is equilateral then it’s sides are equal and angles are equal.
(v) 14 is a divisor of 48 and 28 is not divisible by 82.
Answers:
(i) Let p: An integer is greater than 3
q: An integer is less than 5
r: An integer is multiple of 5
Given[(p ∧ q) → r]
∴ ~ ((p ∧ q) → r] = (p ∧ q) ∧~r
An integer greater than 3 and less than 5 and not divisible by b

(ii) Let P:x is divisible by y
q: x is divisible by a
r: x is divisible by b
Given [p → (q ∧ r)]
∴ ~P (q ∧ r)] = p ∧~(q ∧ ~r)
= p ∧( ~ ( q ∨ ~r)
x is divisible by y and x is not divisible by a or not a multiple of 5

(iii) Let p: Weather is fine
q: Friends are coming
r: we go to a movie
Given[p∧~q ∨~r)]
~(p ∧ (~q ∨ ~r)) ≡ ~p ∨ ~(~ q ∨ ~r) :
≡ ~p ∨ (q ∧ r)

(iv) Let p = a triangle is equilateral
q: Sides are equal
r: angles are equal
Given p → (q ∧ r)
∴ ~(p → (~q ∨ ~r)) ≡ ~p ∧ ~q ∨ ~r)
A triangle is equilateral and sides are not.
equal or angles are not equal.
Let p: 14 is a divisor of 48
q: 28 is divisible by 82
Given p ∧ ~q
∴  ~(p ∧ ~q) ≡ ~p ∨ q
14 is not a divisor of 48 or 28 is divisible by 82

Question 3.
Determine whether the following propositions is a Tautology or a contradiction or neither.
(i) (p ∧ q) ∧ ~p
(ii) [~p ∧ (p ∨ q)]
(iii) (p ∧ q) → (p ∨ q)
(iv) (p ∧ q) →p
(v) ~ p ∧ ~q
Answers:
(i) (p ∧ q) ∧~p

From last column we conculde that it is a contradiction

(ii) [~p ∧ (p ∨ q)]

From last column we conclude it is neither tautology nor a contradiction

(iii) (p ∧ q) → (p ∨ q)

From last column we conclude it is a tautology

(iv) (p ∧ q) → p

From last column we conclude that it is a tautology

(v) ~ p ∧ ~q

It is neither tautology nor contradiction

Part C

2nd PUC Basic Maths Mathematical Logic Ex 6.2 Five Marks Questions and Answers

Question 1.
Check whether the following propositions is a Tautology or a contradiction.
(i) (p ∧ ~q) → (p ∧ q)
(ii) [~p ∧ (p ∨ q)] → q
(iii) (p →q) ↔ (~p →~q)
(iv) [~(p →~q)] ∨ (~ p ↔ q)
(v) (~p ∨ q) ↔ (p ∨~9)
Answers:
(i) (p ∧~q) → (p∧q)

It is neither Tauthology nor contradiction

(ii) [~p ∧ (p ∨ q)] → q

F From last column we conclude it is a tautology

(iii) (p →q) ↔ (~p →~q)

F It is neither a tautology nor contradiction

(iv) [~(p →~q)] ∨ (~ p ↔ q)

It is neither tautology nor contradiction

(v) (~p ∨ q) ↔ (p ∨~9)

It is neither tautology nor contradiction

Question 2.
Show that (p → q) + (~q→~p) is a Tautology.
Answer:

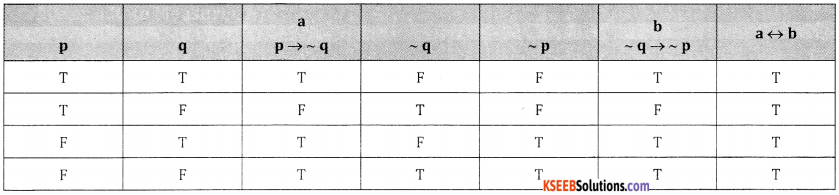
It is a tautology

Question 3.
Show that ~(p ∨ q) →(~p∧~q) is a Tautology.
Answer:

It is a tautology

Question 4.
Prove : [(p →q) ∧ (q →r)] → (P→r) is a Tautology.
Answer:

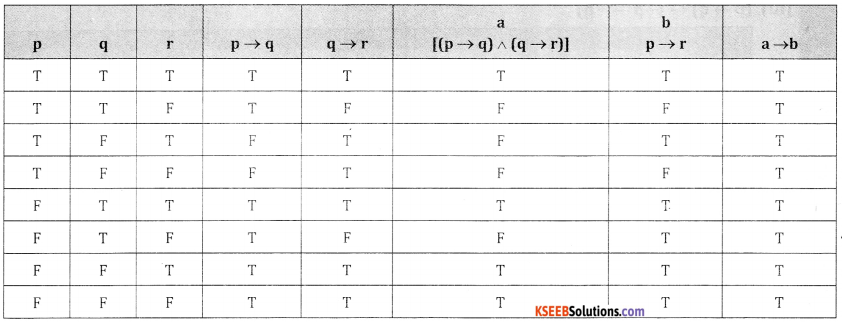
From last column we conclude that it is a tautology

Question 5.
Prove that (p ∨ q) ∧ (~p ∧~q) is a contradiction.
Answer:

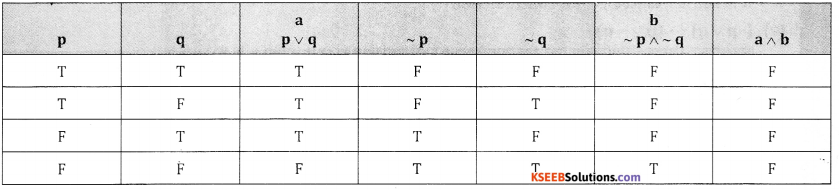
From last column we conculde that it is a contradiction

Question 6.
Show that [(~p ^ q) ^ (q ^ r) ^ (~q)] is a contradiction.
Answer:

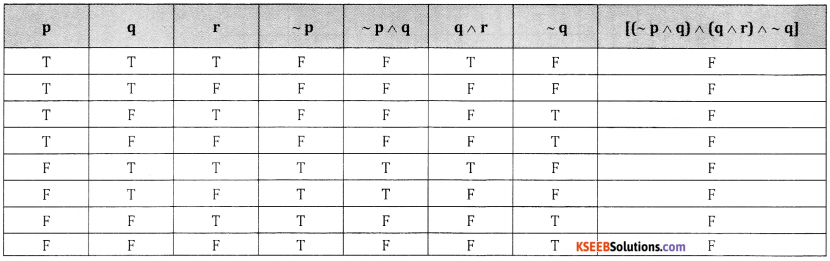
From last column we conclude that it is a contradiction

Question 7.
Examine whether the following are logically equivalent:
(i) p ↔ q and (p → q) ∧ (q → p)
(ii) p → (q → r) and (p → q) → r
(iii) (p ∧ ~q) ∨ q and p ∨ q.
(iv) p ↔ q and (~ p ∨ q) ∧ (~q ∨ p)
(v) p ∧ q and ~(p →~q)
(vi) ~ (p ↔ q ) and (p ∧ ~q) ∨ (q ∧~p)
(vii) p∨ (q ∧ r) and (p ∨ q) ∧ (p ∨ r)

(i)

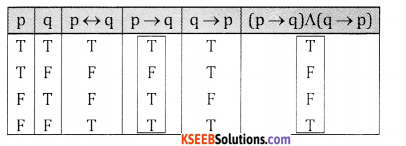
From 3rd & 6th column we conclude that
p ↔ q (p ↔ q) ∧ (q ↔ p)

(ii) p → (q → r) and (p → q) → r

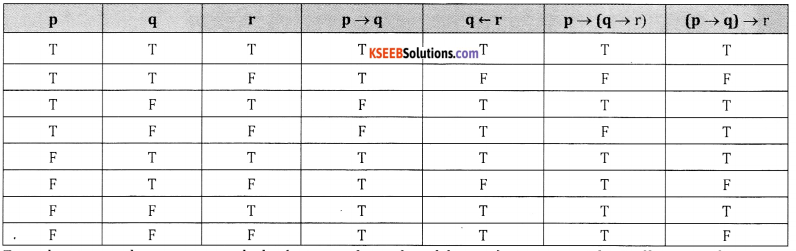
From last two columns we conclude that p → (q → r) and (p → q) → r are not logically equivalent

(iii) (p ∧ ~q) ∨ q and p ∨ q.

From last two columns we conclude (p ∧ ~q) ∨ q p ∨ q.

(iv) p↔ q and (~ p ∨ q) ∧ ( ~q ∨ p)

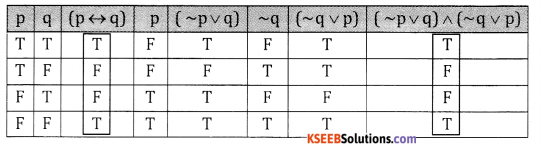
From 3 rd and 8 th columns we conclude that p ↔ q ≡ (~ p ∨ q) ∧ (~q ∨ p)

(v) P ∧ q and (p → ~q)

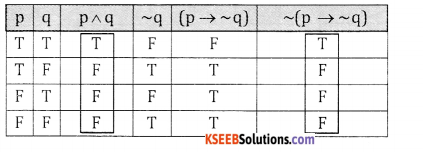
Column 3 and column 6 are identical :
∴ They are logically equivalent

(vi) ~ (p ↔ q ) and (p ∧ ~q) ∨ (q ∧~p)

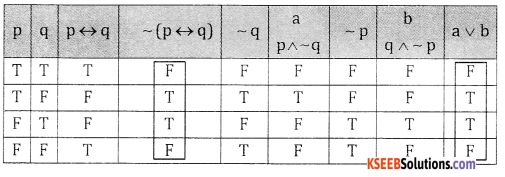
4^th & ^th columns are identical ∴ they are logically equivalent

(vii) p ∨ (q ∧ r) and (p ∨ q)∧ (p ∨ r)

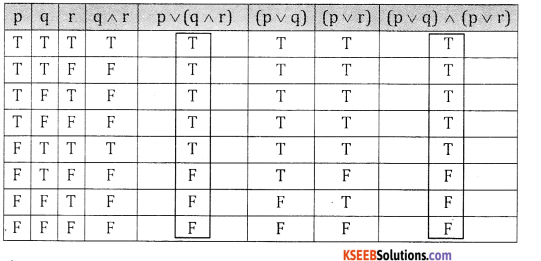
5^th column & 8^th columns are identical
∴ p∨ (q∧r) = (p ∨ q)∧ (p ∨ r)