Students can Download Basic Maths Exercise 7.1 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 7 Ratios and Proportions Ex 7.1
Part – A
2nd PUC Basic Maths Ratios and Proportions Ex 7.1 One Mark Questions and Answers ( 1 × 10 = 10)
Question 1.
If 3:5 is a ratio, find the antecedent and consequent.
Answer:
Antecedent = 3, Consequent = 5.
Question 2.
x gets a salary of7 20,000, y gets a salary of 5,000. Find the ratio of their salaries.
Answer:
Ratio of their salaries is 20000:50000 = 2:5.
Question 3.
Find the inverse ratio of 4:5.
Answer:
Inverse ratio of 4 : 5 is 5 : 4
![]()
Question 4.
A house consumes 30 kgs of wheat and 4kg of sugar compare the consumption of wheat and sugar in the form of ratio.
Answer:
Wheat: Sugar = 30 kg: 4 kg = 15:2. 6.
Question 5.
Mr. X completes a job is 3 hours and Mr. Y completes the same job is 45 minutes compare their performances.
Answer:
3 hrs.: 45 minutes = 3 × 60 : 45 = 180 : 45
= 4:1.
Question 6.
Find the compound ratio of 3 : 4 and 4: 7.
Answer:
Compound ratio = \(\frac{3}{4} \cdot \frac{4}{7}=\frac{3}{7}=3: 7\)
Question 7.
Find the compound ratio of 1:2, 2:3 and 3:5.
Answer:
Compound ratio = \(\frac{1}{2} \times \frac{2}{3} \times \frac{3}{5}=\frac{1}{5}=1: 5\)
Question 8.
Find the duplicate ratio of 5 : 4.
Answer:
Duplicate ratio of 5 : 4 is 52: 42 = 25: 16.
Question 9.
Find the triplicate ratio of 3 : 5.
Answer:
Triplicate ratio of 3 : 5 is 33: 53 = 27 : 125.
Question 10.
Find the subduplicate ratio of 9:49.
Answer:
Subduplicate ratio of 9 : 49 is √9:√49 = 3:7
![]()
Question 11.
Find the subtriplicate ratio of 125: 64.
Answer:
Subtriplicate ratio of 125 : 64
= 3√125:3√64 = 5:4
Question 12.
Find the value of x of 5 : 20 = 3 :x.
Answer:
5x = 20 x 3⇒ x = \(\frac{20 \times 3}{5}=\) = 12 ⇒ X = 12
Part – B
2nd PUC Basic Maths Ratios and Proportions Ex 7.1 Two Marks Questions and Answers (2 × 10 = 20)
Question 1.
Find the ratio between two numbers such that their sum is 40 and their difference is 8.
Answer:
Let the two numbers be x & y
Given x + y = 40 ……. (1)
& x – y = 8 … (2)
Solving we get
Adding 2x = 48 ⇒ x = 24 & y = 40 – 24 = 16
∴Ratio of the numbers is 24 : 16 ⇒ 3:2.
Question 2.
A ratio is the lowest term is 3:8. If the difference between the quantities is 25. Find the quantities.
Answer:
Let the numbers are 3x and 8x
Given 8x – 3x = 25
5x = 25 ⇒ X = 5
∴ Two numbers are 3(5) & 8(5)
i.e., 15 and 40.
![]()
Question 3.
Two numbers are is the ratio 3:5. If 5 is added to each , they are is the ratio. 2:3 find the numbers.
Answer:
Let two numbers be 3x & 5x
If 5 is added to each then \(\frac{3 x+5}{5 x+5}=\frac{2}{3}\)
9x + 15 = 10x + 10
x = 5
∴ The two numbers are 3(5) & 5(5) = 15 & 25.
Question 4.
What must be added to each term is the ratio 2 : 3 so that is becomes 5:6.
Answer:
Let x must be added to each term of 2 : 3 then
\(\frac{2+x}{3+x}=\frac{5}{6}\)
⇒ 12 + 6x = 15 + 5x
x = 3.
Question 5.
What must be added to each term is the ratio 4:5 so that is becomes 7:8.
Answer:
Let x must be added to each of 4:5 then
\(\frac{7-x}{4-x}=\frac{5}{2}\)
x = 3
![]()
Question 6.
What must be subtracted from each term is the ratio 7:4 so that it becomes 5:2.
Answer:
Let x must be subtracted from each of 7 : 4 then \(\frac{7-x}{4-x}=\frac{5}{2}\)
⇒ 14 – 2x = 20 – 5x 5x – 2x = 20 – 14
3x = 6 ⇒ x= 2.
Question 7.
What must be subtracted from each term is the ratio 8:7 so that it becomes 4:3.
Answer:
Let x must be subtracted from each of 8:7 then
\(\frac{8-x}{7-x}=\frac{4}{3}\)
24 – 3x = 28 – 4x
4x – 3x = 28 – 24
x = 4
![]()
Question 8.
If a: b = 2:3, b:c=3:5 and c:d= 5:7 find a:d.
Answer:


Question 9.
If a: b = 2:3 and b:c= 6:13 find a:b:c.
Answer:
Given
\(\frac{a}{b}=\frac{2}{3}, \frac{b}{c}=\frac{6}{13} \)
\(\frac{a}{b}=\frac{2 \times 2}{2 \times 2}=\frac{4}{6} \)
∴ a:b:c = 4 : 6 : 13
Question 10.
If a : b = 3:4, b:c=8 = 15 find a:b:c.
Answer:
\(\frac{a}{b}=\frac{3}{4}, \frac{b}{c}=\frac{8}{15}\)
\(\frac{a}{b}=\frac{3 \times 2}{4 \times 2}=\frac{6}{8} \frac{b}{c}=\frac{8}{15}\)
∴ a : b : c = 6 : 8 : 15
Part-C
2nd PUC Basic Maths Ratios and Proportions Ex 7.1 Three Marks Questions and Answers (3 × 16 = 48)
Question 1.
Divide 1800 is the ratio 3 : 4 : 5.
Answer:
Sum of the ratios 3 + 4 + 5 = 12
∴ \(\frac{3}{12}\) × 1800 = 450
\(\frac{4}{12}\)1800 = 600
\(\frac{4}{12}\)1800 = 750
![]()
Question 2.
If x : y = 3; 4 find \(\frac{2 x^{2}+3 y^{2}}{x^{2}+y^{2}}\)
Answer:

Question 3.
If a:b= 2:3 and x:y = 4:7.
Find \(\frac{5 a x+4 b y}{8 a x+3 b y}\)
Answer:

Question 4.
The angles of a triangle are in the ratio 3:4:5. Find the angles.
Answer:
Sum of the ratios 3 + 4 + 5 = 12
W. K. T sum of the angles of a triangle = 75°
∴ \(\frac{3}{12}\) × 180 = 45°, 12
\(\frac{3}{12}\) × 180 = 60°,
\(\frac{3}{12}\) × 180 = 75°
∴ The three angles of a triangle are 45°, 60°, 75°
![]()
Question 5.
An article is sold at 40% gain an the cost price. Find the ratio of the selling price and cost price.
Answer:
An article is sold at 40% gain
100 + 40 = 40
If the cost price is 100 then the selling price 100 + expenditure is 4x – 1000 40 = 140
∴ \(\frac{S P}{C P}=\frac{140}{100}=\frac{7}{5}\)
∴ SP : CP = 7 : 5
Question 6.
If the monthly incomes of A and B are is the ratio 3:4 and their expenditures are is the ratio 1 :2. If each saves 1000 find the monthly incomes.
Answer:
Let monthly income of A is 3x and expenditure
is 3x – 1000 and monthly income of B is 4x and
Given \(\frac{3 x-1000}{4 x-1000}=\frac{1}{2}\)
6x – 4000 = 4x – 2000
⇒ 2x = 2000 ⇒ x = 1000
∴ The monthly income of A = 3x = 3 × 1000 = 3000
∴ The monthly income of B is 3(500) = 2000.
Question 7.
If the monthly incomes of A and Bare in the ratio 3:4 and their expenditure are in the ratio 1:2.If each saves 2000. Find their monthly incomes.
Answer:
Let their monthly incomes are 3x and 4x and their expenditure are 3x – 2000 and 4x – 2000
Given difference of their squares is \(\frac{3 x-2000}{4 x-2000}=\frac{1}{2}\)
6x – 4000 = 4x – 2000
⇒ 2x = 2000 ⇒ x = 1000
The monthly income of A = 3x = 3 × 1000 = 3000
The monthly income of B = 4x = 4 x 1000 = 4000
Question 8.
Two numbers are is the ratio 6:7. If the difference of their squares is 117 find the two numbers.
Answer:
Let the two numbers are 6x and 7x
i.e., (7x)2 – (6x)2= 117
49x2 – 36x2= 117
13x2 = 117
⇒ x = 6
∴ The numbers are 3(6) and 46) = 18 and 21.
![]()
Question 9.
Two numbers are is the ratio 3:4. If the sum of their squares is 900 find the two numbers.
Answer:
Given \(\frac{x}{y}=\frac{3}{4}, \frac{y}{z}=\frac{7}{9}\)
Given sum of their squares = 900
(3x)2 + (4x)2= 900
9x2 + 16x2 = 900
25x2 = 900
⇒ x2 = \(\frac{900}{25}\) = 36 ⇒ x = 6
∴ The numbers are 3(6) and 4 (6) = 18 and 24
Question 10.
If x:y= 3:4 and y:z= 7:9. Find x:y:z.
Answer:

Part – D
2nd PUC Basic Maths Ratios and Proportions Ex 7.1 Five Marks Questions and Answers (5 × 16 = 80)
Question 1.
Divide ₹ 800 is three parts such that three times of the first, five times of the second and six times the third are equal.
Answer:
Let the 3 parts be x, y and z
Given 3x = 5y = 62
Let 3x = 6z and 5y = =\(\frac{6}{5} \)z
x = 2z, y = 2
∴ x : y : z = 2z : \(\frac{6}{5}\)z : z= 10:6:5
Sum of the ratios = 10 + 6 + 5 = 21
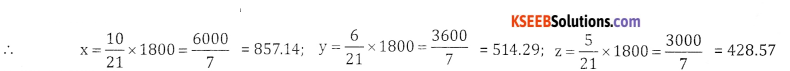
Question 2.
Divide ₹ 3262 among x, y and z such that if ₹35, ₹15 and ₹12 are deducted from their respective shares, the remainders are in the ratio 3:5:8.
Answer:
x + y + z = 3262 and x – 35:y – 15: Z – 12 = 3:5:8 x-35 3 y-155 y -15 5
![]()
5x – 175 = 3y – 45,
5x – 3y = 130,
5x = 130 + 3y,
x= 26+\(\frac{3}{5} \)y
8y – 120 = 52 – 60
8y – 5z = 60
5z = 8y – 60
z = \(\frac{8}{5} \)y – 12
Substitute for x and z
Buty x + y + z = 3262
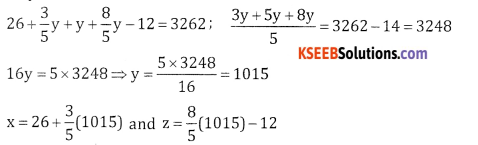
= 26 + 609
x = 635
x = 635, y = 1015 and z = 1612
z = 1624 – 12
z = 1612
![]()
Question 3.
If x:y= 2:3. Find the value of \(\frac{2 x^{3}+3 y^{3}}{x^{3}+y^{3}}\)
Answer:

Question 4.
Divide 5880 is to three parts, such that ‘B’ receive thrice as ‘A’ and C receives \(\frac{5^{t h}}{6}\) of what B receives.
Answer:
Let A receive ₹x and B receives ₹ 3x and C receive \(\frac{5}{6}\)(3x) = \(\frac{5}{2}\)x
∴ A:B:C= 1:3:\(\frac{5}{2}\)= 2:6:5
∴ A’s share = \(\frac{2}{13}\) × 5880 = 904.6
B’s share = \(\frac{6}{13}\) x 5880 = 2713.8 :
C’s share = \(\frac{5}{13}\)x 5880 = 2261.5
Question 5.
If \(\frac{2 x^{2}+3 y^{2}}{x^{3}+y^{2}}=\frac{2}{41}\) Find x:y.
Answer:

Question 6.
Divide 6000 into three parts is the ratio \(\frac{1}{2}: \frac{1}{3}: \frac{1}{6}\)
Answer:
Given \(\frac{1}{2}: \frac{1}{3}: \frac{1}{6}\) multiply by 6, we get 3:2:1
1st part = \(\frac{3}{6}\) × 6000 = 3000
2nd part = \(\frac{3}{6}\) × 6000 = 2000
3rd part = \(\frac{3}{6}\) × 6000= 1000
![]()
Question 7.
Divide 17,640 a many P, Q, R and S such that O gets \(7^{\text {th }}5\) of P, R gets \(5^{\text {th }}8\) of Q and S gets \(\frac{2^{t h}}{13}\) of the sum of Q and R.
Answer:
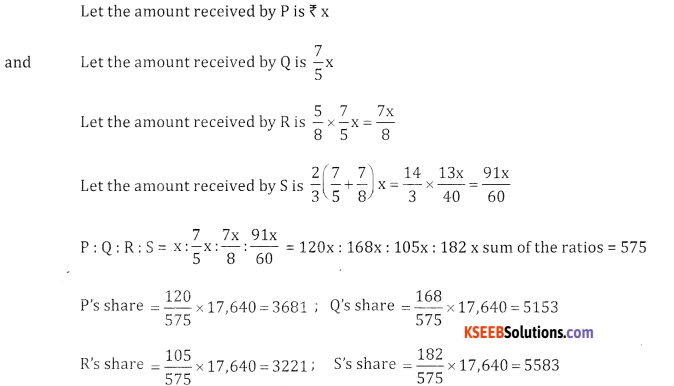
![]()
Question 8.
The Rajdhani express takes 18 hours to reach Delhi from Bhubaneshwar while Nilachala Express takes
24 hours for the same of Delhi is 2880 kms from Bhubaneshwar find the ratio between the average speeds of the two trains.
Answer:
Distance Speed = \frac{\text { Distance }}{\text { Time taken }}
Speed of Ragdhari express =\(=\frac{2880}{18}\)
Speed of Nilachala express = \(\frac{2880}{24}\)
Ratio of average speed = \(\frac{2880}{18}: \frac{2880}{24}\) = 24:18 = 4:3