Students can Download 2nd PUC Maths Model Question Paper 2 with Answers, Karnataka 2nd PUC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Model Question Paper 2 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 100
Instructions:
- The question paper has five parts namely A, B, C, D and E. Answer all the parts.
- Use the graph sheet for the question on Linear programming in PART E.
Part – A
I. Answer all the questions ( 10 × 1 =10 )
Question 1.
A Relation R on A = {1,2,3} defined by R = {(1,1) (1,2) (3,3)} is not symmetric, Why?
Answer:
The Relation R is defined by R = {.(1,1) (1,2) (3,3)} for Symmetric Relation if (1,2)∈R then (2,1) ∈R but (2,1) ∉ R?
∴ R is not Symmetric Relation.
Question 2.
Write the domain of f(x) = cos-1 x.
Answer:
The domain of cos-1x is [-1,1]
Question 3.
Define a scalar matrix.
Answer:
A diagonal matrix in which all the Principle diagonal Elements are equal is called scalar matrix.
![]()
Question 4.
If A = \(\left[ \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right] \) find |2A|.
Answer:

Question 5.
If y = log (sin x) find \(\frac{\mathrm{dy}}{\mathrm{d} \mathrm{x}}\)
Answer:
y = log(sin x)
Differentiae w.r.t.x, we get
\(\frac{\mathrm{dy}}{\mathrm{d} \mathrm{x}}\) = \(\frac{1}{\sin x}\) . cosx = cotx
\(\frac{\mathrm{dy}}{\mathrm{d} \mathrm{x}}\) = cot x
Question 6.
Evaluate ∫( sin x + cos x) .dx.
Answer:
∫(sinx + cosx).dx
= ∫ sin x.dx + ∫ cos x.dx.
= -cosx + sin x + c
= sinx – cosx + c
![]()
Question 7.
Find the direction cosines of the vector \(\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}\)
Answer:
\(\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}\)

Question 8.
Find the equation of the plane with intercept 4 on z-axis and parallel to xoy plane.
Answer:
∴ The Required Equation of the plane is z =4.
Question9.
Define feasible region.
Answer:
The Common Region determined by all the cons traints including the noh-negative constraints (x ≥ 0, y ≥ 0) of a linear programming problem is called the feasible region.
Question 10.
If P(A) = \(\frac{4}{5}\) and P(B/A) = \(\frac{2}{5}\) find
P(A∩B)
Answer:
P(A /B) = \(\frac{P(A \cap B)}{P(A)}\)
∴ P(A∩B) = P(B/A).P(A)
= \(\frac{2}{5} \cdot \frac{4}{5}=\frac{8}{25}\)
∴ P(A∩B) = \(\frac{8}{25}\)
![]()
Part – B
II. Answer any TEN questions : ( 10 × 2 = 20 )
Question 11.
Verify whether the operation * defined on Q by a*b = \(\frac{\mathrm{ab}}{2}\) is associative or not.
Answer:
* is defined on Q by a*b = \(\frac{\mathrm{ab}}{2}\) for associative we have to prove that
a* (b* c) = (a* b)* c
∴ a*(b*c) = a * \(\frac{\mathrm{ab}}{2}\) b*c = \(\frac{\mathrm{bc}}{2}\)
= \(\frac{\mathrm{abc}}{4}\) ……………….. (1)
(a*b)*c = \(\frac{\mathrm{ab}}{2}\) *c
= \(\frac{\mathrm{abc}}{4}\) ……………….. (2)
∴ from (1) and (2)
∴ * is Associative
∴ * Satisfies the associative property.
Question 12.
Write the simplest form of
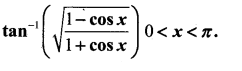
Answer:

Question 13.
Evaluate
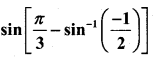
Answer:

Question 14.
Find the equation of line joining (1,2) and (3,6) using determinants.
Answer:
Let P (x,y) be any point on AB. Then Area of triangle ABP is is “O”

x(2 – 6) – y(1 – 3) + 1(6 – 6) = 0
-4x + 2y = 0
2x – y = 0
![]()
Question 15.
If y + siny = cosx find \(\frac{d y}{d x}\)
Answer:
y + siny = cos x
Differentiate w.r.t. x
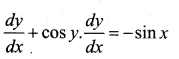
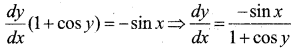
Question 16.
If y = xx find \(\frac{d y}{d x}\).
Answer:
y = xx
Take logarithm on Both side, we get
logy = logxx ⇒ logy=xlogx
Differentiate wr.t. x
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x x \(\frac{1}{x}\) + log x
\(\frac{d y}{d x}\) = y[1 + logx]
\(\frac{d y}{d x}\) = xx[1 + logx]
Question 17.
Find the approximate charge in the volume v of a cube of side x metres caused by increasing the sind by 2%.
Answer:
w.r.t volume of a cube = v = x3.
⇒ \(\frac{d v}{d x}\) = 3x2 dx
Δx = 0.02 x
∴ dv = ( \(\frac{d v}{d x}\) ) Δx = (3x2) Δx = 3x2 x 0.02x
= 0.06 x3m3
![]()
Question 18.
Evaluate \(\int \frac{\sin ^{2} x}{1+\cos x} d x\)
Answer:
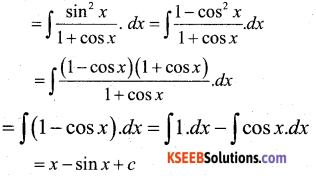
Question 19.
Evaluate \(\int_{1}^{e} \frac{1}{x} \cdot d x\)
Answer:
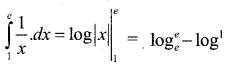
Question 20.
Find the order and degree of the differential equation.
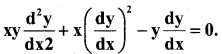
Answer:
Order -2, Degree – 1
Question 21.
If \(\overrightarrow{\mathrm{a}}\) is a Unit Vector such that
( \(\vec{x}-\vec{a})(\vec{x}+\vec{a}\)) = 8 find | \(\overrightarrow{\mathbf{x}}\) )
Answer:

Question 22.
Find the area of a parallelogram whose adjacent sides are given by the vectors
\(\overrightarrow{\mathrm{a}}=3 \hat{\mathrm{i}}+\hat{\mathrm{j}}+4 \hat{\mathrm{k}} \cdot \overrightarrow{\mathrm{b}}=\hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}\)
Answer:
The area of a parallelogram with \(\vec{a}\) and
\(\vec{b}\) as its adjacent sides is given by | \(\vec{a} \times \vec{b}\) |

Question 23.
Find the angle between the pair of lines.
\(\vec{r}\) = 3î + 2 ĵ – 4k̂ + λ (î + 2ĵ + 2k̂) and
\(\vec{r}\) = 5î + 2 ĵ + λ (3î + 2 ĵ + 6k̂)
Answer:
Here
\(\vec{b}_{1}\) = î + 2 ĵ + 2k̂ and \(\vec{b}_{1}\) = 3î + 2 ĵ + 6k̂
The angle θ between the two lines is given

Question 24.
Find the probability ditribution of number of heads in two tosses of a coin.
Answer:
When a coin is tossed twice the sample space is S = {HH,HT, TH,TT}
Let x denote the number of heads in any out come in s.
∴x(HH) = 2
x(HT) = 1
x(TH) = 1
x(TT) = 0
P(x = 0) = P(TT) = \(\frac{1}{4}\)
P(x = 1) P(HT,TH) = \(\frac{2}{4}\) = \(\frac{1}{2}\)
P(x = 2) P(HT,TH) = \(\frac{1}{4}\)
Probability distribution of x is
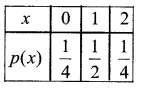
Part – C
III. Answer any TEN questions : ( 10 × 3 = 30 )
Question 25.
Find gof and fog if 1:R → R and g: R → R are given by f(x) = cosx and g(x) = 3x2 show that gof ≠ fog.
Answer:
f(x) = cosx
g(x)=3x2
gof(x) = g[f(x)]
= g[cosx]
= 3cos2x
fog(x) = f[g(x)]
= f[3x2]
= cos3x2
fog ≠ gof
Question 26.
P.T. 3cos-1x=cos-1(4x3 – 3x) x ∈ \(\frac{1}{2}\) , 1
Answer:
cos-1 x = A Now \(\frac{1}{2}\) ≤ x ≤ 1
cosA = x
cos3A = 4cos3 A – 3cosA ⇒\(\frac{1}{2}\) ≤ A < 1
cos3A=4x3 – 3x
3A = cos -1(4x3 – 3x) ⇒ 0 ≤ A ≤ \(\frac{\pi}{3}\)
3cos-1x = cos-1 [4x3 – 3x] ⇒ 0 ≤ 3A ≤ π
Question 27.
By using Elementary transformations
find the iii,e of the matrix
A = missing
In order to use elementary row operation
A = IA

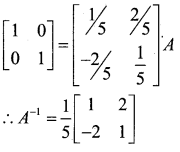
Question 28.
Find \(\frac{d y}{d x}\) if x = a(cosθ + θsinθ) and dx
y = a(sinθ – θcosθ)
Answer:
x = a(cosθ + θsinθ)
Diff w.r.t θ we have
\(\frac{d x}{d \theta}\) = a(-sinθ + θcosθ + sinθ )
\(\frac{d x}{d \theta}\) = a[θcosθ]
y = a(sinθ – θcosθ)
w.r.t θ
\(\frac{d y}{d \theta}\)
= a[cosθ – θ x sin θ – cosθ]
\(\frac{d y}{d \theta}\) = a[sinθ]
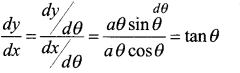
∴ \(\frac{d y}{d x}\) = tan θ
![]()
Question 29.
Verify Rolle’s theorem for the function y = x2 + 2, x ∈[-2,2]
Answer:
The function y = x2 +2 is continuous in [-2,2], and differentiable in (-2,2)
Also f (-2) ⇒ f (x) = x2 + 2
f(- 2) = (-2)2 + 2
= 4 + 2 = 6
f(2) = 22 + 2 = 6
∴ f(-2) = f(2) = 6
∴ The value of f(x) at -2 and 2 coincide.
∴ Rolle’s Theorem states that there is a point
c ∈ (-2,2) where f'(c) = 0
Since f'(x) = 2x, we have
f’ (c) = 2c
2c = 0
c = 0
∴ we have c = 0 ∈ (-2,-2)
Question 30.
Find the interval in which the function f given by f (x) = x2 – 4x + 6 is
(i) Strictly increasing.
(ii) Strictly decreasing.
Answer:
f(x) = x2 – 4x + 6
Differentiate w.r.t x
f'(x) = 2x – 4
∴ f'(x) = 0 gives
0 = 2x – 4
2x = 4
x = 2
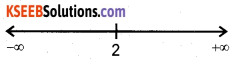
∴ The point x = 2 divides the real line into two disjoint intervas namely, (-∞,2) and (2,∞).
The interval (-∞, 2) f'(x) = 2x – 4 < 0.
∴ f is strictly decreasing in (-∞, 2). Also in the interval (2,∞) f'(x)>0 and so the function f is strictly increasing in (2,∞).
Question 31.
Find \(\int \frac{\left(x^{2}+1\right) \cdot e^{x}}{(x+1)^{2}} \cdot d x\)
Answer:


Question 32.
Evaluate ∫tan -1x.dx.
Answer:
∫tan -1x.dx.
= ∫xtan -1x. ∫tan -1dx + c
Apply Rule of integration by parts by taking tan-1 x as the first function.

Question 33.
Find the area of the region bounded by the curve y = x2 and the line y = 4.
Answer:
y = x2 represents the parabola symmetrical about y – axis
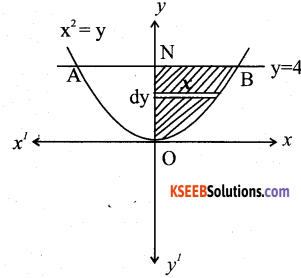
∴ The Area of the region AOBA is given by 2 \(\int_{0}^{4} x \cdot d y=2\) [Area of the region BONB bounded by curve, y-axis and the lines y=0 and y=4]
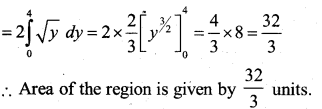
Question 34.
Form the differential equation representing the family of curves y=mx where m is arbitrary constant.
Answer:
The given family of curves represents the equation of straight lines.
∴ y = mx ……………………. (1)
Differentiate w.r.t x, we get dy
\(\frac{d y}{d x}\) = m
∴ substitute m = \(\frac{d y}{d x}\), we have
y = mx
⇒ y = \(\frac{d y}{d x}\) x
\(\frac{d y}{d x}\) = \(\frac{y}{x}\)
\(\frac{d y}{d x} – \frac{y}{x}\) = 0
which is the required differential equation.
Question 35.
Prove that
![]()
Answer:
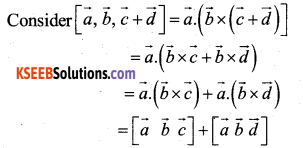
Question 36.
If \(\vec{a}=2 \vec{i}+2 \hat{j}+3 \hat{k} \overrightarrow{\mathbf{b}}=-\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+\hat{\mathbf{k}} and [latex]\overrightarrow{\mathbf{c}}=3 \hat{\mathbf{i}}+\hat{\mathbf{j}}\) are such that \(\overrightarrow{\mathbf{a}}+\lambda \overrightarrow{\mathbf{b}}\) is perpendicular to \(\overrightarrow{\mathrm{c}}\). Then find the value of λ.
Answer:

Question 37.
Find the distance of a point (2, 5, -3) from the plane \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}+2 \hat{k})=4\)
Answer:
\(\vec{a}=2 \hat{i}+5 \hat{j}-3 \hat{k}\)
\(\vec{N}=6 \hat{i}-3 \hat{j}+2 \hat{k}\)
d = 4
distance of a point from a plane is
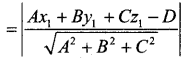
∴ The distance of the point (2, 5 – 3) from the
given plane is
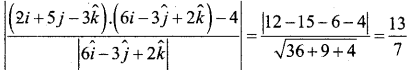
Question 38.
A die is tossed thrice. Find the probability of getting an odd number at least once.
Answer:
When a dice is tossed thrice, the sample space, is S = {(x,y,z):x,y z e (1,2,3,4,5,6}}
which contains 6 x 6 x 6 = 216 Equally likely sample points.
Let E : “an odd number at least once”
E1 : not an odd number any time
E1 : “An even number on all throws”
E1 = {(x,y,z):x,y,ze{2,4,6}j
e1 contains 3x3x3=27 equally likely simple events.
Required probability = P(E) = 1 – P(E).
= \(1-\frac{27}{216}=1-\frac{1}{8}=\frac{7}{8}\)
![]()
Part – D
IV. Answer any SIX questions : ( 6 × 5 =30 )
Question 39.
Prove the function f : N → Y defined by f(x) = 4x + 3, where Y = {y : Y = 4x + 3, x∈N} is invertible. Also write the inverse of f(x).
Answer:
f:N→y defined by
f(x) = 4x + 3
and Assume a an inverse f-1:y → N. is defined by f-12y) = x.
∴ wk.t
f(x) = 4x + 3
y = 4x + 3
y – 3 = 4x
x = \(\frac{y-3}{4}\)
and wk 7
f-1(y) = x
f-1(y) = \(\frac{y-3}{4}\) f-1 = g
or
g(y) = \(\frac{y-3}{4}\)
∴ To S.T. it exist inverse.
To prove it is inversible.
We have to prove that
fog(x) = x
gof(y) = y

To find the inverse of a function :
f-1:y → N. by f-1(y) = x
f-1(y) = \(\frac{y-3}{4}\)
Question 40.
If A = \(\left[ \begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix} \right]\) B = \(\left[ \begin{matrix} 2 & 0 \\ 1 & 3 \end{matrix} \right]\) and C = \(\left[ \begin{matrix} 1 & 1 \\ 2 & 3 \end{matrix} \right]\) Calculate AC BC and (A+B).C. Also verify that (A+B). C = AC+BC.
Answer:

From (1) and (2)
(A+B). C = AC+BC.
Question 41.
Solve the following system of equations by matrix method. x-y + z = 4, 2x + y – 3y = 0 andx + y + z =2.
Answer:
The given system can be written as AX = B

The given system is consistent and has a unique Solution.
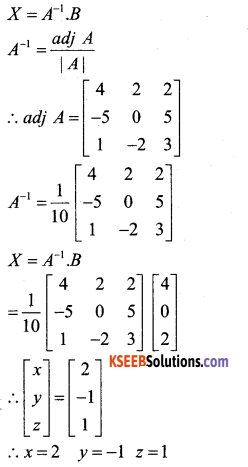
![]()
Question 42.
If y = 3e2x+2e3x P.T. \(\frac{d^{2} y}{d x^{2}}\) – \(\frac{d y}{d x}\) + 6y = 0
y = 3e2x + 2e3x
Differentiate w.r.t x.
\(\frac{d y}{d x}\) = 6e2x + 6e3x
Again Diff w.r.t x
\(\frac{d^{2} y}{d x^{2}}\) = 12e2x + 18e3x
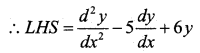
= 12e2x +183x – 5 ((5e2x + 6e3x) + 6(3e2x + 2e3x)
= 12e2x + 183x – 30e2x – 30e3x +18e2x + 12e3x
= 30e2x + 30e3x – 30e2x – 30e3x
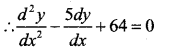
Question 43.
A ladder 24 ft long leans against a vertical wall. The lower end is moving away at the rate of 3ft/sec. Find the rate at which the top of the ladder is moving down wars. If its foot is 8ft from the wall.
Answer:
The foot of the ladder is at a distance x from the wall and the top is at a height y at instant of time t. then
(24)2 = x2 + y2
Diff w.r.t time, we get
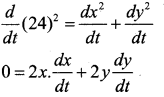
given \(\frac{d x}{d t}\) = 3ft / sec. dt
and x = 8 ft.
y2 = (24)2 – x2
= (24)2 – (8)2
= 576 – 64
y2 = 512
y = √512
0 = 2 × 8 × 3 + 2 × √5I2 \(\frac{d y}{d t}\)
= 48 + 2√512
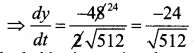
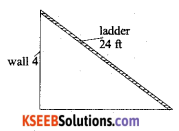
∴ The ladder is moving downwards at rate of \(\frac{24}{\sqrt{512}}\) ft/ sec. or 1.06100 ft / sec.
Question 44.
Find \(\int \frac{d x}{x^{2}-a^{2}}\) and hence evaluate \(\int \frac{d x}{3 x^{2}+13 x-10}\)
Answer:


Question 45.
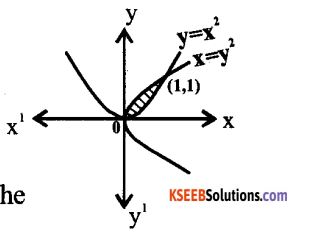
Find the area of the region bounded by the two parabolas y = x2 and y2 = x.
Answer:
The given two curves are parabola y = x2 and y2 = x
The point of intersection of these two parabolas are 0 (0,0) and A (1,1) as shown in the fig.
We can set
y2 =x or y = √x – f (x)
y – x2 = g(x) where
f(x) ≥ g(x) in [0,1]
∴ The required area of the Shaded Region
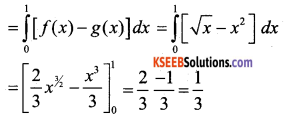
∴The Required area of the Region is = \(\frac{1}{3}\) units.
![]()
Question 46.
Find the general solution of the differential equation. e/tany. dx + (1 -ex). sec2y.dy = 0
Answer:
ex. tany dx + (1-ex). sec2 y dy = 0 (1)
Separating the variables and integrating, we get
This can be done by divide throughout (l-ex)t any Eqn. (1) becomes and integrate
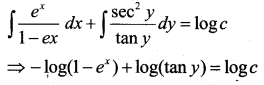
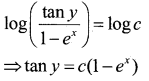
Which is the required solution.
Question 47.
Derive the equation of the plane in normal form both in the cartesian and vector form.
Answer:
Consider a plane whose perpendicular distance from the origin is d. where d ≠ 0.
If \(\overrightarrow{\mathrm{ON}}=d \hat{\mathrm{n}}\)
Let p be any point on the plane Therefore NP.OP=0(l)

lx + my + nz = d
This is the Required Equation of a plane in normal form.
To find P and Q :
x2 = 4y and x = 4y – 2
(4y – 2)2 = 4y
⇒ 16y2 + 4 – 16y = 4y
⇒ 16y2 – 20y + 4 =0
⇒ (y – 1) (16y – 4) =0
⇒ y =1 (or) y = 1/4
Ify=1; x = 2 ⇒ 2 (2,1)
and y = 1/4 x = -1 (-1, 1/4)
Thus , the points of Intersection are
(2,1) 1 (-1.,1/4)
∴ Area of the Region O B Q C = Area of BCQ+ Area of QCO.

Question 48.
A person buys a lottery ticket in 50 lotteries in each of which his chance of winning a prize is \(\frac{1}{100}\) what is the probability that he will win a prize exactly once?
Answer:
Given it is a lax of Bemoullian trials with n = 50 and P = \(\frac{1}{100}[latex]
Hence q = 1 – P = 1 – [latex]\frac{1}{100}\) = \(\frac{99}{100}\)
The Probability that he will win a prize exactly once is
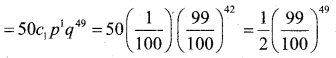
Part – E
V. Answer any ONE questions : ( 1 × 10 = 10 )
Question 49.
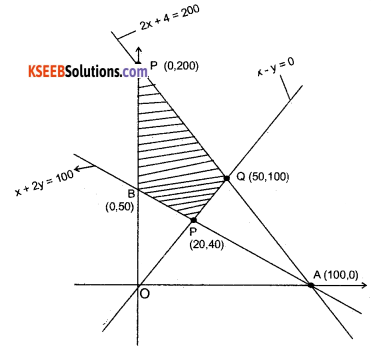
a) Minimize and maximize Z = x + 2y subject to the constraints,
x + 2y ≥ 100
2x – y ≤ 0
2x + y ≤ 200
x, y ≥ 0 by graphical method.
Our problem is to minimize and maximize
Z = x + 2y …………..(1)
Subject to constraints are
x + 2y ≥ 100 …………….(2)
2 x – y ≤ 0 ……………..(3)
2x + y ≤ 200…………….(4)
x> 0, x>0…………….(5)
∴ x + 2y- 100 which passes through the points A( 100,0) and B(0,50)
2x – y = 0 which passes through the points (0,0) and (20,4 0)
2x + y = 200 which passes through the points A(100,0)&C (0,200)
∴ The comer points of feasible region are 5(0,50) P(20,40) 0(50,100) and C(0,200).
At B (0,50) ⇒ Z = 0 + 2 × 50 = 100
At P(20,40) ⇒ Z = 20 + 2 × 40 – 100
At Q(5O,1OO) ⇒ Z = 50 + 2 × 100 = 250
At C(0,200) Z = 0 + 2 × 200 = 400
Hence max Z = 400 at (0, 200) and
Min Z = 100 at B and also at P.
(b)
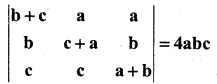
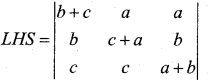
R1 R1 – (R2 + R3)
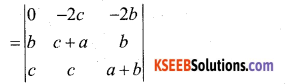
= 0 [(c + a) (a + b) – bc) + 2c (b (a + b) – bc) – 2b (bc – (c + a)]
= 0 + 2c [ab + b2 -bc] – 2b [bc – c2 -ac]
= 2abc + 2cb2 – 2bc2 – 2b2c + 2bc2 + 2abc
= 4 abc = RHS
![]()
Question 50.
a) Prove that \(\int_{0}^{a} f(x) \cdot d x=\int_{0}^{a} f(a-x) \cdot d x\) and hence evaluate \(\int_{0}^{\pi / 4} \log (1+\tan x) \cdot d x\)
Answer:
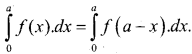
put t = a- x
x = a – t
than dt = -dx
when x = 0 x = a
t = a t = 0
then

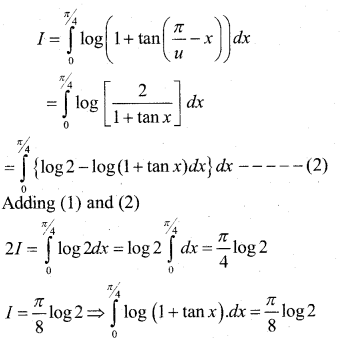
(b) Find the value of k, if
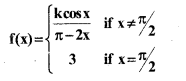
Answer:
