Students can Download 2nd PUC Maths Previous Year Question Paper March 2020, Karnataka 2nd PUC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Previous Year Question Paper March 2020
Time: 3 Hrs 15 Min
Max. Marks: 100
Instructions:
- The question paper has five parts namely A, B, C, D, and E. Answer all the parts.
- Use the graph sheet for the question on Linear programming in Part E
Part – A
Answer ALL the following questions: (10 × 1 = 10)
Question 1.
Let * be the binary operation on N given by a * b = LCM of a and b. Find 5 * 7.
Solution:
5 * 7 = LCM of 5 and 7 = 35
Question 2.
Write the range of the function y = sec-1 x.
Solution:
[0, π] – {\(\frac{\pi}{2}\)}
Question 3.
If a matrix has 5 elements, what are the possible orders it can have?
Solution:
1 × 5 and 5 × 1
![]()
Question 4.
Find the values of x for which \(\left|\begin{array}{cc}x & 2 \\18 & x\end{array}\right|=\left|\begin{array}{cc}6 & 2 \\18 & 6\end{array}\right|\)
Solution:
x2 – 36 = 36 – 36
⇒ x2 = 36
⇒ x = ±6
Question 5.
If y = tan(√x), find \(\frac{d y}{d x}\).
Solution:
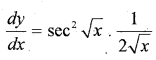
Question 6.
Find ∫(2x2 + ex) dx.
Solution:
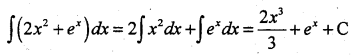
Question 7.
Define the Negative of a vector.
Solution:
A vector whose magnitude is the same as that of a given vector but direction is opposite to that of it is called negative of a vector.
![]()
Question 8.
If a line makes angles 90°, 135° and 45° with the X, Y and Z-axes respectively, find its direction cosines.
Solution:
Let direction cosines of the line be l, m and n with the X, Y, and Z-axes respectively, and given that
α = 90°, β = 135° and γ = 45°
Then, l = cos α = cos 90° = 0
m = cos β = cos 135° = \(-\frac{1}{\sqrt{2}}\)
and n = cos γ = cos 45° = \(\frac{1}{\sqrt{2}}\)
Therefore, the direction cosines of the line are 0, \(-\frac{1}{\sqrt{2}}\) and \(\frac{1}{\sqrt{2}}\).
Question 9.
Define optimal solution in Linear Programming Problem.
Solution:
Any feasible solution of LPP which maximizes or minimizes the objective function is called an optimal solution.
Question 10.
If P(A) = \(\frac{3}{5}\) and P(B) = \(\frac{1}{5}\). find P(A ∩ B) if A and B are independent events.
Solution:
P(A ∩ B) = P(A) × P(B) = \(\frac{3}{5} \times \frac{1}{5}=\frac{3}{25}\)
Part – B
Answer any TEN questions: (10 × 2 = 20)
Question 11.
If f : R → R and g : R → R are given by f(x) = cos x and g(x) = 3x2. Find gof and fog.
Solution:
gof(x) = g[f(x)] = g[cosx] = 3cos2 x
fog(x) = f[g(x)] = f[3x2] = cos 3x2
![]()
Question 12.
Prove that cot-1(-x) = π – cot-1 x, ∀ x ∈ R.
Solution:
Let cot-1(-x) = α
⇒ -cot α = -x
⇒ -cot α = x
⇒ cot(π – α) = x
⇒ π – α = cot-1 x
⇒ α = π – cot-1 x
⇒ cot-1 (-x) = π – cot-1 x
Question 13.
Find the value of sin-1(sin \(\frac{3 \pi}{5}\))
Solution:
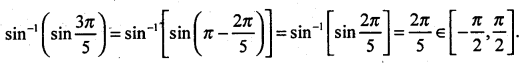
Question 14.
Find the area of the triangle whose vertices are (-2, -3), (3, 2) and (-1, -8) using the determinant method.
Solution:
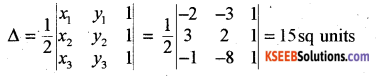
Question 15.
Find \(\frac{d y}{d x}\), if sin2 x + cos2 y = 1.
Solution:
2 sin x cos x + 2 cos y(-sin y) \(\frac{d y}{d x}\) = 0
⇒ \(\frac{d y}{d x}=\frac{2 \sin x \cos x}{2 \sin y \cos y}=\frac{\sin 2 x}{\sin 2 y}\)
Question 16.
If y = xx, find \(\frac{d y}{d x}\).
Solution:

Question 17.
Find the interval in which the function f given by f(x) = x2 – 4x + 6 is strictly decreasing.
Solution:
We have f(x) = x2 – 4x + 6
⇒ f'(x) = 2x – 4
Therefore, f'(x) = 0 gives x = 2.
Now the point x = 2 divides the real line into two disjoint intervals namely (-∞, 2) and (2, ∞).
In the interval (-∞, 2), f'(x) = 2x – 4 < 0. Therefore, f is strictly decreasing in this interval. Also, in the interval (2, ∞) f'(x) > 0 and so the function f is strictly increasing in this interval.
![]()
Question 18.
Find ∫cot x log(sin x) dx.
Solution:
Put log sin x = t
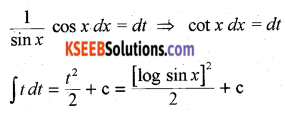
Question 19.
Find ∫x sec2 x dx.
Solution:
x tan x – log |sec x| + c
Question 20.
Find the order and degree (if defined) of the differential equation:
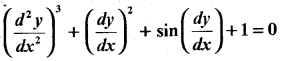
Solution:
Order = 2, Degree is not defined.
Question 21.
Find the projection of the vector \(\vec{a}=\hat{i}+3 \hat{j}+7 \hat{k}\) on the vector \(\vec{b}=7 \hat{i}-\hat{j}+8 \hat{k}\).
Solution:

Question 22.
Find the area of the parallelogram whose adjacent sides are determined by the vectors \(\vec{a}=\hat{i}-\hat{j}+3 \hat{k}\) and \(\vec{b}=2 \hat{i}-7 \hat{j}+\hat{k}\)
Solution:
Area = \(|\vec{a} \times \vec{b}|\) = 15√2 sq.units
Question 23.
Find the equation of the plane with intercepts 2, 3 and 4 on the X, Y and Z-axes respectively.
Solution:
\(\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1\)
![]()
Question 24.
A random variable X has the following probability distribution:
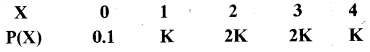
Find the value of K.
Solution:
ΣP(x) = 1
⇒ 0.1 + K + 2K + 2K + K = 1
⇒ 0.1 + 6K = 1
⇒ 6K = 1 – 0.1 = 0.9
⇒ K = 0.9/6 = 0.15
Part – C
Answer any TEN questions: (10 × 3 = 30)
Question 25.
Show that the relation R defined in the set A of all triangles as R = {(T1, T2); T1 is similar to T2} is an equivalence relation.
Solution:
T1 is similar to T2 ⇒ R is reflexive.
Let (T1, T2) ∈ R ⇒ T1 is 111 to T2
⇒ T2 111 T1
⇒ (T2, T1) ∈ R
∴ R is symmetric
Let (T1, T2) ∈ R; (T2, T3) ∈ R
⇒ T1 is 111 to T2 and T2 is 111 to T3
⇒ T1 is 111 to T3
⇒ (T1, T2) ∈ R
∴ R is transitive
∴ R is an equivalence relation.
![]()
Question 26.
Prove that \(2 \tan ^{-1}\left(\frac{1}{2}\right)+\tan ^{-1}\left(\frac{1}{7}\right)=\tan ^{-1}\left(\frac{31}{17}\right)\)
Solution:

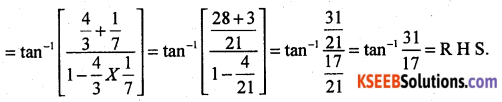
Question 27.
If F(x) = \(\left[\begin{array}{ccc}\cos x & -\sin x & 0 \\\sin x & \cos x & 0 \\0 & 0 & 1\end{array}\right]\) then show that F(x) F(y) = F(x + y).
Solution:

Question 28.
If x = 2at2, y = at4 then find \(\frac{d y}{d x}\)
Solution:
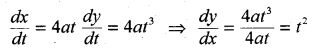
Question 29.
Verify Mean Value Theorem for the function f(x) = x2 – 4x – 3, x ∈ [1, 4].
Solution:
f(x) is a polynomial in x.
It is continuous in {1, 4} and differentiable in {1, 4) and f'(x) = 2x – 4.
There exists at least one value c ∈ (1, 4) such that f'(c) = \(\frac{f(b)-f(a)}{b-a}\)
a = 1, f(a) = f(1) = 12 – 4(1) – 3 = 1 – 4 – 3 = 1 – 7 = -6
b = 4, f(b) = f(4) = 42 – 4(4) – 3 = 16 – 16 – 3 = -3
f'(c) = 2c – 4
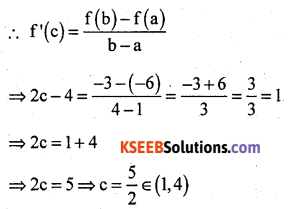
Mean Value theorem is verified.
Question 30.
Use differential to approximate √36.6.
Solution:

Question 31.
Find \(\int \frac{(x-3)^{e^{x}}}{(x-1)^{3}} d x\)
Solution:

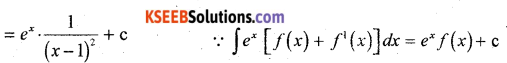
Question 32.
Evaluate: \(\int_{0}^{\pi / 2} \cos ^{2} x d x\)
Solution:
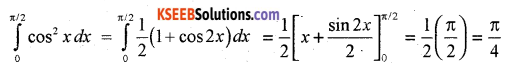
Question 33.
Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axes in the first quadrant.
Solution:
The given curve x2 = 4y is a parabola which is symmetrical about Y-axis (∵ it contains even power of x) only and passes through the origin.
The area of the region bounded by the curve x2 = 4y, y = 2 and y = 4 and the Y-axis are shown in the figure.
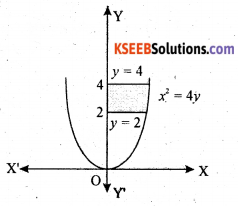
Required area (shaded region) = \(\int_{y=a}^{y=b}|x| d y\)
(Here, |x| = √4y and a = 2, b = 4)
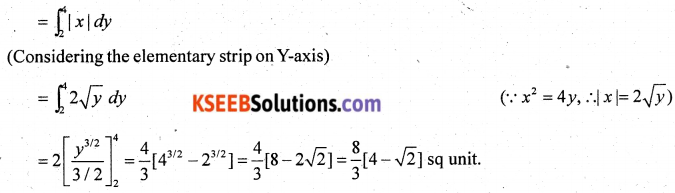
Question 34.
Find the equation of a curve passing through the point (-2, 3), given that the slope of the tangent to the curve at any point (x, y) is \(\frac{2 x}{y^{2}}\).
![]()
Question 35.
Find a unit vector perpendicular to each of the vector \((\vec{a}+\vec{b})\) and \((\vec{a}+\vec{b})\) where \(\vec{a}=3 \hat{i}+2 \hat{j}+2 \hat{k}\) and \(\vec{b}=\hat{i}+2 \hat{j}-2 \hat{k}\).
Solution:


Question 36.
Find x such that the four points A(3, 2, 1), B(4, x, 5), C(4, 2, -2) and D(6, 5, -1) are coplanar.
Solution:

Question 37.
Find the equation of the plane through the intersection of the planes 3x – y + 2z – 4 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).
Question 38.
A man is known to speak truth 3 out of 4 times. He throws a dice and reports that it is a six. Find the probability that it is actually a six.
Solution:
P(S1) = Probability that six occurs = \(\frac{1}{6}\)
P(S2) = Probability that six does not occur = \(\frac{5}{6}\)
P(E | S1) = Probability that man reports that six occurs when six has actually on the die = Probability that the truth occurs = \(\frac{3}{4}\)

Part – D
Answer any SIX questions: (6 × 5 = 30)
Question 39.
Show that the function f : R → R given by f(x) = 4x + 3 is invertible. Find the inverse of f.
Solution:
Let f(x1) = f(x2) = 4x1 + 3 = 4x2 + 3
⇒ 4x1 = 4x2
⇒ x1 = x2
∴ f is one-one.
Let y ∈ Y ∃ x ∈ N such that y = 4x + 3
∴ f is onto.
∴ f is bijective.
Consider an arbitrary element y of Y. By the definition of Y, y = 4x + 3, for some x in the domain N.
x = \(\frac{y-3}{4}\)
Define a function g : Y → N by g(y) = \(\frac{y-3}{4}\)
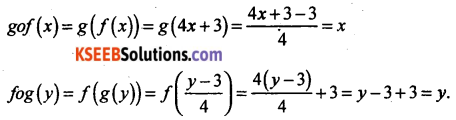
⇒ gof = IN and fog = IY
⇒ f is invertible and g is the inverse of f.
∴ f-1 = g.
![]()
Question 40.
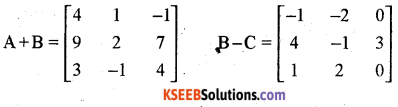
If A = \(\left[\begin{array}{ccc}1 & 2 & -3 \\5 & 0 & 2 \\1 & -1 & 1\end{array}\right]\), B =\(\left[\begin{array}{ccc}3 & -1 & 2 \\4 & 2 & 5 \\2 & 0 & 0\end{array}\right]\) and C =\(\left[\begin{array}{ccc}4 & 1 & 2 \\0 & 3 & 2 \\1 & -2 & 3\end{array}\right]\) then compute (A + B) and (B – C). Also verify that A + (B – C) = (A + B) – C. Also verify (A + B) C = AC + BC.
Solution:

Question 41.
Solve the following system of linear equations by matrix method:
2x + 3y + 3z = 5
x – 2y + z = -4
3x – y – 2z = 3
Solution:


x = 1, y = 2, z = -1
Question 42.
If y = (tan-1 x)2, show that (x2 + 1)2 y2 + 2x(x2 + 1) y1 = 2
Solution:

Question 43.
Sand is pouring from a pipe at the rate of 12 cm3/sec. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
Solution:
Let r be the radius, h be the height and V be the volume of sand cóne at any time t.

Hence, when the height of the sand cone is 4 cm, its height is increasing at the rate of \(\frac{1}{48 \pi}\) cm/s
Question 44.
Find the integral of \(\frac{1}{x^{2}+a^{2}}\) w.r.t x and hence evaluate \(\int \frac{1}{x^{2}+2 x+2} d x\)
Solution:
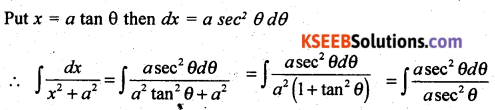
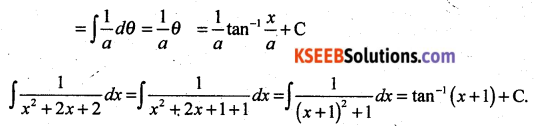
Question 45.
Using the method of integration, find the area of the smaller region bounded by the ellipse \(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\) and the line \(\frac{x}{3}+\frac{y}{2}=1\)
Solution:

Question 46.
Find the general solution of the differential equation x\(\frac{d y}{d x}\) + 2y = x2 log x.
Solution:


![]()
Question 47.
Derive the equation of a line in space passing through a given point and parallel to a given Vector and Cartesian form.
Solution:
Vector Form
Let \(\vec{a}\) be the position vector of the given point A with respect to the origin O of the rectangular
coordinate system. Let l be the line which passes through point A and is parallel to a given vector \(\vec{b}\). Let \(\vec{r}\) be the position vector of an arbitrary point P on the line Fig.
Then \(\vec{AP}\) is parallel to the vector \(\vec{b}\), i.e., \(\overrightarrow{\mathrm{AP}}=\lambda \vec{b}\), where λ is some real number.
But \(\overrightarrow{\mathrm{AP}}=\overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{AO}}\)
i.e., \(\lambda \vec{b}=\vec{r}-\vec{a}\)
Conversely, for each value of the parameter λ, this equation gives the position vector of a point P on the line. Hence, the vector equation of the line is given by
\(\vec{r}=\vec{a}+\lambda \vec{b}\) ……. (1)
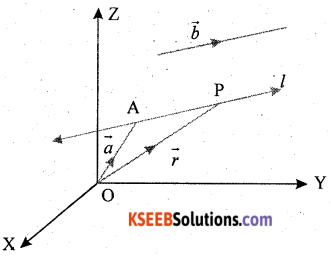
Cartesian Form
Let the coordinates of the given point A be (x1, y1, z1) and the direction ratios of the line be a, b, c.
Consider the coordinates of any point P be (x, y, z). Then \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k} ; \vec{a}=x_{1} \hat{i}+y_{1} \hat{j}+z_{1} \hat{k}\) and \(\vec{b}=a \hat{i}+b \hat{j}+c \hat{k}\)
Substituting these values in (1) and equating the coefficients of \(\hat{i}, \hat{j} \text { and } \hat{k}\), we get
x = x1 + λa ; y = y1 + λb ; z = z1 + λc …….. (2)
These are parametric equations of the line. Eliminating the parameter λ from (2), we get
\(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\)
This is tle Cartesian equation of the line.
Question 48.
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is \(\frac{1}{100}\). What is the probability that he will win a prize (a) exactly once (b) at least once?
Solution:
Let X denotes the number of wins
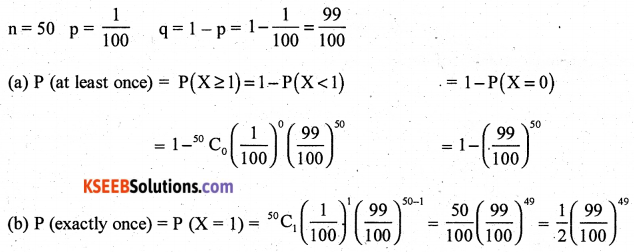
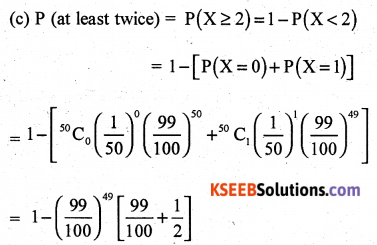
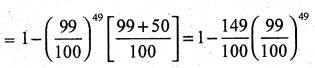
Part – E
Answer any ONE question: (1 × 10 = 10)
Question 49(a).
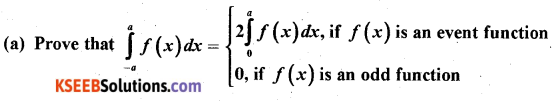
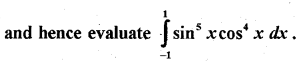
Solution:

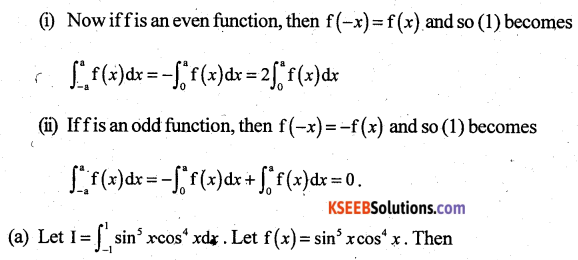

Question 49(b).
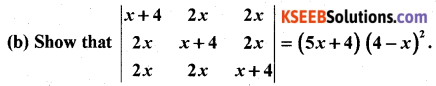
Solution:


![]()
Question 50(a).
Maximise z = 4x + y Subject to constraints: x + y ≤ 50, 3x = y ≤ 90, x ≥ 0, y ≥ 0 by graphical method.
Solution:
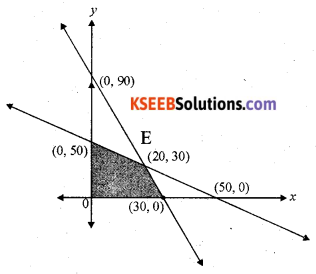

Optimal Solution:
Z is maximum at D(30, 0) & Zmax = 120
Question 50(b).
Find the value of K,
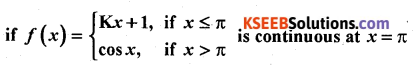
Solution:
