Students can Download Maths Chapter 1 Relations and Functions Ex 1.1 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 1 Relations and Functions Ex 1.1
2nd PUC Maths Relations and Functions NCERT Text Book Questions and Answers Ex 1.1
Question 1.
Determine whether each of the following relations are reflexive, symmetric and transitive:
(i) Relation R in the set A = {1,2,3,13,14} defined as R = {(x, y): 3x – y = 0}
Answer:
A = {1, 2, 3,………. 14}
R={(x, y) : 3x – y = 0}
= {(x, y) : y = 3x)
R : {(1,3), (2,6), (3,9), (4,12)}
R is not reflexive as (1,1) ∉ R
R is not symmetric as (1,3) ∈ R but (3,1) ∉ R
R is not transitive as (1,3) ∈ R, (3,9) ∈ R but (1, 9) ∉ R.
To disprove, any counter example is sufficient.
(ii) Relation R in the set N of natural numbers defined as
R = {(x, y) : y = x + 5 and x < 4}
Answer:
A = {1, 2, 3,………… }
R = {(1,6), (2,7), (3,8)} because x < 4
R is not reflexive as (1,1) ∈ R
R is not symmetric as (2,7) ∈ R but (7,2) ∉ R
R is Transitive as transitivity is not contradicted.
(iii) Relation R in the set A = {1,2,3,4,5,6} as R = {(x, y) : y is divisible by x}
Answer:
A = {1,2,3,4,5,6}
R={(1, 1),(1,2) …………………… }
As x is divisible by x, (x, x) ∈ R hence R is reflexive.
(3, 6) ∈ R but (6, 3) ∈ R
i.,e 6 is divisible by 3 but 3 is not divisible by 6,hence R is not symmetric
y is divisible by x, z is divisible by y, then z is divisible by x
i.e. (x, y) ∈ R, (y, z) ∈ R ⇒ (x, z) ∈ R hence R is transitive.
![]()
(iv) Relation R in the set Z of all integers defined as R = {(x, y) : x -y is an integer)
Answer:
R is reflexive as x – x = 0 ∈ Z, ∀ x ∈ Z
R is symmetric as x – y ∈ z ⇒ y – x ∈ z
i.e. (x, y) ∈ z ⇒(y – x) ∈ Z
R is transitive as x – y ∈ z, y – x ∈ Z then (x – y) + (y – z) ∈ Z
i.e. (x – z) ∈ Z
i.e. (x, y) R (y, z) ∈ R ⇒ (x, z) ∈ R.
(v) Relation R in the set A of human beings in a town at a particular time given by
(a) R = {(x, y): x and y work at the same place}
Answer:
R is reflexive as x and x work at the same place
R is symmetric as x and y work at the same place
⇒ y and x work at the same place R is transitive as transitivity does not contradict.
(b) R s {(x, y) : x and y live in the same locality}
Answer:
R is reflexive, symmetric and transitive (same proof like (a))
(c) R = {(x, y) : x is exactly 7 cm taller than y}
Answer:
x is not exactly 7 cm taller than x
i.e. (x, x) ∉ R, hence not reflexive
x is 7 cm taller than y does not imply
y is 7 cm taller than x
i.e. (x, y) ∈ R⇒(y, x) ∈ R
Hence not symmetric. Similarly R is not Transitive
(d) R = {(x, y): x is wife of y}
Answer:
x can’t be the wife of x, hence (x, x) ∉ R,
∴ R is not reflexive.
x is the wife of y⇒y is the wife of x
hence (x, y) ∈ R ⇒(y, x) ∈ R.
hence R is not symmetric
R is transitive as it does not contradict transitivity.
![]()
(e) R = {(x, y): x is father of y}
Answer:
As x can’t be the father of x
(x, x) ∉ R, hence not reflexive.
If x is the father of y then y can’t be the father of x.
i.e. (x, y) ∈ R ⇒(y, x) ∈ R
hence R is not symmetric
x is the father of y, y is the father of z then x is not the father of z
i.e. (x, y) ∈ R (y, z) ∈ R ⇒(x, z) ∈ R
hence R is not transitive.
Question 2.
Show that the relation R in the set R of real numbers, defined as R = {(a, b) : a < b2}, is neither reflexive nor symmetric nor transitive.
Answer:
\(\frac{1}{2} \) \(\frac{1}{4} \)Not reflexive
a = 2, b = 5 ⇒ (a, b) : 2 ≤ 25, is true
but (b, a) : 5 <4 is not true
hence (a, b) ∈ R⇒(b, a): Not symmetric
a = 3, b = -2, c = -1
(a, b) ∈ R, (b, c) ∈ R
⇒ 3 ≤ 4, -2 ≤ 1
(a, c) ∈ R ⇒ 3 ≤ 1 which is not true
hence (a, b) ∈ R , (b, c) ∈ R⇒(a, c) ∈ R : not transitive.
Question 3.
Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive.
Answer:
R = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}
R is not reflexive as (1, 1) ∉ R
R is not symmetric as (1, 2) ∈ R ⇒(2,1) ∈ R
R is not transitive as (2, 3) ∈ R, (3, 4)e R ⇒(2,4) ∈ R
Question 4.
Show that the relation R in R defined as R = {(a, b) : a <, b}, is reflexive and transitive but not symmetric.
Answer:
(a, a): a ≤ a is true ∀ a ∈ R
hence reflexive
(a, b) ⇒ a ≤ b ⇒b ⇒(b,a) ∈ R
hence R is not symmetric
i.e. (1,3) ⇒ 1 ≤ 3 but (3, 1)⇒3≤1
(a, b) ⇒ a ≤ b, (b, c) ⇒ b ≤ c ⇒ a ≤ c = (a, c) ∈ R
hence R is transitive.
Question 5.
Check whether the relation R in R defined by R = {(a, b) : a < b3} is reflexive, symmetric or transitive.
Answer:
\(a=\frac{1}{3}, \frac{1}{3}\) \(\frac{1}{27}\)
(a, a) ∈ R ∴ not reflexive
a= 1, b = 2
(a,b) ∈ R ⇒<8
(b, a) ∈ R ⇒2 ≤ 1, which is not true
(a, b) ∈ R ⇒ (b, a) ∈ R, hence not symmetric
a = 60, b = 4, c = 3
60 ≤ 43, 4 ≤ 33 ⇒60 ≤ 33
(a, b) ∈ R, (b, c) ∈ R ⇒(a, c) ∈ R. hence R is not transitive.
![]()
Question 6.
Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.
Answer:
(1, 1) ∉ R, hence not reflexive (1, 2) ∈ R
⇒ (2, 1) ∈ R, also (2, 1) ∈ R ⇒ (1,2) ∈ R .
(a, b) ∈ R = 9 (b, a) ∈ R, hence symmetric
(1,2) ∈ R (2, 1) ∈ R but (1, 1) ∈ R hence not transitive.
Question 7.
Show that the relation R in the set A of all the books in a library of a college, given by R = {(x, y) : x and y have same number of pages} is an equivalence relation.
Answer:
(x, x) ∈ R as x and x have same number of pages. ∀ x ∈ A, hence Reflexive
(x, y) ∈ R ⇒ x and y have same number of pages
⇒ y and x have same number of pages
⇒ 9 (y, x) ∈ R hence Symmetric (x, y) ∈ R and (y, z) ∈ R
⇒ x and y and y and z have same number of pages
⇒ x and z have same number of pages
⇒ 9 (x, z) ∈ R, hence Transitive.
Since R is reflexive, symmetric and transitive, R is an equivalence Relation.
Question 8.
Show that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a, b) : |a – b| is even}, is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.
Answer:
(a, a) ∈ R |a – a| =0 is even, which is true
R is reflexive,
a R b and b R c
⇒ |a – b| is even and |b – c| is even
⇒ (a- b) is even and b – c is even
⇒ (a- b) + (b – c) is even
⇒ (a- c) is even ⇒ |a – c| is even
⇒ a R c, hence R is transitive
since R is reflexive, symmetric and transitive
R is an equivalence relation.
|1 – 3| = 2, even, |1 – 5| = 4, even |3 – 5| = 2,
even hence all the elements of {1, 3, 5} are related to each other.
|2 – 4| = 2, even, hence all the elements {2,4} are related to each other.
|1-2| = 1, |3-2| = 1, |5-2| = 3, |1-4| = 3,
|3 – 4| = 1, |5 – 4| = 1, are all odd. Therefore no elements of {1, 3, 5} are related to {2, 4}.
![]()
Question 9.
Show that each of the relation R in the set
A = {x ∈ Z : 0 ≤ x ≤ 12}, given by
(i) R = {(a, b): |a – b| is a multiple of 4}
(ii) R = {(a, b) : a = b} is an equivalence relation. Find the set of all elements related to 1 in each case.
Answer:
A = {0, 1,2,3………… 12}
(i) a R a ⇒ | a – a| = 0 is a multiple of 4 ∀ a ∈ A hence R is reflexive
a R b ⇒ a – b = multiple of 4
⇒ |-(b – a)| = multiple of 4
⇒ |b – a| is a multiple of 4
⇒b R a, hence R is symmetric a R b and b R c
⇒ |a -b| is a multiple of 4 and |b – c| is a multiple of 4
⇒ (a-b) and (b – c) are multiple of 4
⇒ a – b + b – c = a – c is a multiple of 4
⇒ |a – c| is a multiple of 4 ⇒ a R c
hence R is transitive.
Since R is reflexive, symmetric and transitive R is an equivalence relation.
a R 1 ⇒ |a – 1| = m (4)
⇒ a = 1, 5, 9 as
|1 – 1| = 0, |5 – 1| = 4, |9 – 1|= 8 are multiple of 4.
Hence elements related to 1 are {1, 5,9}
(ii) a R a ⇒ a = a ∀ a ∈ A
hence R is reflexive
a R b ⇒ a = b
⇒ b = a ⇒ b R a, hence R is symmetric a R b and b R c
⇒ a = b and b = c
⇒ a = c, = a R c
hence R is transitive
Therefore R is an equivalence Relation,
a R 1 ⇒ a = 1
Therefore the elements related to 1 is {1}
Question 10.
Give an example of a relation. Which is
(i) Symmetric but neither reflexive nor transitive.
Answer:
(1, 1) ∉ R, hence not reflexive (1, 2) ∈ R
⇒ (2, 1) ∈ R, also (2, 1) ∈ R
⇒ (1,2) ∈ R .
(a, b) ∈ R = 9 (b, a) ∈ R, hence symmetric
(1,2) ∈ R (2, 1) ∈ R but (1, 1) ∈ R hence not transitive.
(ii) Transitive but neither reflexive nor symmetric.
Answer:
Relation R in the set N of natural numbers defined as
R = {(x, y) : y = x + 5 and x < 4}
Answer:
A = {1, 2, 3,………… }
R = {(1,6), (2,7), (3,8)} because x < 4
R is not reflexive as (1,1) ∈ R
R is not symmetric as (2,7) ∈ R but (7,2) ∉ R
R is Transitive as transitivity is not contradicted.
![]()
(iii) Reflexive and symmetric but not transitive.
Answer:
R = {(1, 1), (2, 2), (3, 3), (2, 3), (3, 2), (1,2), (2,1)}
(1, 2) ∈ R, (2,3) ∈ R ⇒(1, 3) ∉ R
(iv) Reflexive and transitive but not symmetric.
Answer:
(a, a): a ≤ a is true ∀ a ∈ R
hence reflexive
(a, b) ⇒ a ≤ b ⇒b ⇒(b,a) ∈ R
hence R is not symmetric
i.e. (1,3) ⇒ 1 ≤ 3 but (3, 1) ⇒3≤1
(a, b) ⇒ a ≤ b, (b, c) ⇒ b ≤ c ⇒ a ≤ c = (a, c) ∈ R
hence R is transitive.
(v) Symmetric and transitive but not reflexive.
Answer:
R = (1, 2), (2, 1), (1, 1), (2, 2)} an A= {1,2,3}
(3, 3) ∉ R, hence not reflexive.
Question 11.
Show that the relation R in the set A of points in a plane given by R = {(P, Q) : distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set of all points related to a point P*(0, 0) is the circle passing through P with origin as centre.
Answer:
Let the origin be 0
R={(P, Q): |0 P| = |0 Q|}
(P, P) ∈ R ⇒ |o p| = |o p| which is true
hence R is reflexive
(P, Q) ∈ R =|0 P| = |0 Q|
⇒ |o Q| = |o p|
⇒ (Q, P) ∈ R
hence R is symmetric (P, Q) ∈ R and (Q, R) ∈ R
⇒ |o p| = |o q| and |o q| = |o r|
⇒ |o p| = |o r|
⇒ (P, R) ∈ R
hence R is transitive.
∴ R is an equivalence relation.
set of points related to P ≠ 0
= {Q ∈ A : (Q, P) ∈ R
= | Q ∈ A : |0 Q| = |0P|}
= {Q ∈ A : Q lies on a circle through P and with center 0}.
![]()
Question 12.
Show that the relation R defined in the set A of all triangles as R = {(T1,T2): T2 is similar to T2}, is equivalence relation. Consider three right angle triangles T2 with sides 3, 4, 5, T2 with sides 5, 12, 13 and T3 with sides 6, 8,10. Which triangles among T1, T2 and T3 are related?
Answer:
(T1, T1) ∈ R ⇒ T1 is similar to T1 which is true. Hence R is reflexive
(T1, T2)∈ R ⇒ T1 is similar to T2
⇒ T2 is similar to T1
⇒ (T2, T,) ∈ 2
hence R is symmetric
(T1, T2) ∈ R, (T2, T3) ∈ R
⇒ T is similar to T2, T2 is similar to T3
⇒ T1 is similar to T3
⇒(T1,T3) ∈ R
hence R is transitive
∴ R is an equivalence Relation.
T1 is similar to T3 as hence T1 and T3 are related.
Question 13.
Show that the relation R defined in the set A of all polygons as R = {(P1, P2) : P3 and P2 have same number of sides}, is an equivalence relation. What is the set of all elements in A related to the right angle triangle T with sides 3, 4 and 5?
Answer:
(P, P) ∈ R as P and P have same number of sides hence R is reflexive.
(P, Q) ∈ R ⇒ P and Q have same number of sides
⇒ Q and P have same number of sides
⇒ (Q,P) ∈ R
hence R is symmetric
(P, Q) ∈ R and (Q, R) ∈ R
⇒ P and Q have number of sides, Q and R have same number of sides. P and R have same number of side
⇒ (P, R) ∈ R
hence R is transitive
∴ R is an equivalence Relation
T is a Triangle
(P, T) ∈ R
⇒ P and T have same number of sides
⇒ P is also a triangle
∴ set of all elements related as T is the set of all triangle in A.
![]()
Question 14.
Let L be the set of all lines in XY plane and R be the relation in L defined as R = {(L1 ,L2) : L1 is parallel to L2}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x + 4.
Answer:
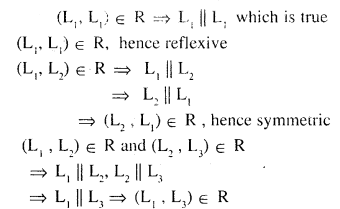
hence R is transitive hence it is equivalence relation
Let L be the required line
= {L : L is parallel to y = 2x + 4}
= {L:L is a line whose relation is y : 2x + k where k is any real}
Question 15.
Let R be the relation in the set (1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4,4), (1, 3), (3, 3), (3, 2)}. Choose the correct answer.
(A) R is reflexive and symmetric but not transitive.
(B) R is reflexive and transitive but not symmetric.
(C) R is symmetric and transitive but not reflexive
(D) R is an equivalence relation.
Answer:
R is reflexive and transitive
(1, 2) ∈ R (2, 1) ≠ R , hence not symmetric
“B” is the correct answer.
Question 16.
Let R be the relation in the set N given by R = {(a, b) : a = b – 2, b > 6}. Choose the correct answer.
(A) (2, 4) ∈ R
(B) (3, 8) ∈ R
(C) (6, 8)∈ r
(D) (8, 7) ∈ r
Answer:
(6, 8) g R
⇒ 6 = 8 – 2 and 8 > 6
“C” is the correct answer.