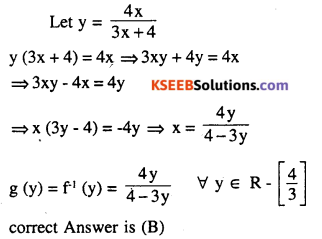Students can Download Maths Chapter 1 Relations and Functions Ex 1.3 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 1 Relations and Functions Ex 1.3
2nd PUC Maths Relations and Functions NCERT Text Book Questions and Answers Ex 1.3
Question 1.
Let f: {1, 3, 4} → {1,2, 5} and g : {1, 2, 5} {1,3} be given by f= {(1,2), (3,5), (4,1)} and
g = {(1, 3), (2, 3), (5,1)}. Write down gof.
Answer:
gof (1) = g (f (1)) = g (2) = 3 gof (3)
= g {f (3)} = g (5) = 1
= gof (4) = g (f (4)) = g (1) = 3
∴ gof = {(1,3), (3,1), (4,3)}
Question 2.
Let f, g and h be functions from R to R. Show that
(f + g)oh =foh + goh
(f.g)oh = (foh) . (goh)
Answer:
∀ x ∈ R
{(f + g)oh} (x) = (f + g) h (x)
= f (h (x)) + g (h (x)) = foh (x) + goh (x)
= {foh + goh} (x)
∴ (f + g) oh = foh + goh
((fg )oh) (x) = (f.g) (h (x))
= fh (x). gh (x)
= {foh (x)} . {goh (x)}
{foh. goh} (x)
(fg) oh = (foh) (goh)
![]()
Question 3.
Find gof and fog, if
(i) f(x) = |x| and g(x) = |5x – 2|
Answer:
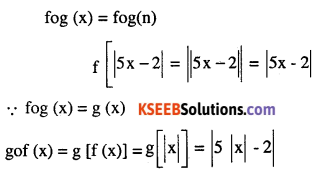
(ii) f (x) = 8x3 and g(x) = \(x^{\frac{1}{3}}\)
Answer:

Question 4.
If \(f(x)=\frac{(4 x+3)}{(6 x-4)}, x \neq \frac{2}{3}\),show that fof(x)= x,for all
\(x \neq \frac{2}{3}\),what is the inverse of f?
Answer:
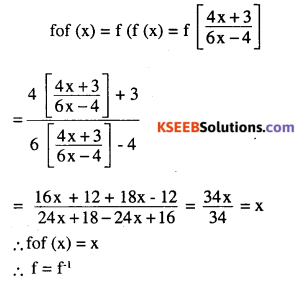
Question 5.
State with reason whether following functions have inverse
(i) f : {1,2, 3, 4} → {10} with
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
(ii) g : {5, 6, 7, 8} → {1, 2, 3, 4} with
g = {(5, 4), (6, 3), (7, 4), (8, 2)}
(iii) h : {2, 3, 4, 5} → {7, 9,11,13} with
h = {(2, 7), (3, 9), (4, 11), (5, 13)}
Answer:
(i) f (1) = f (2) = f (3) = f (4) = 10
⇒ f is not one-one
∴ f does not have an inverse
(ii) g(5) = 4 g(6) = 3 g(7) = 4 g(8) = 2 g(5) = g(7) = 4
∴ g is not one-one, hence g does not have inverse
(iii) h(2) = 7, h(3) = 9, h(4) = 11, h(5)=13,
∴ h is one-one
Also range of h = {7,9,11,13} = co-domain
⇒ h is onto
Hence h has an inverse
h-1 = {(7,2), (9,3), (11,4), (13, 5)}.
![]()
Question 6.
Show that f: [-1,1] → R, given by f(x) =\(\frac{x}{(x+2)}\) is one-one. Find the inverse of the function f : [-1,1] → Range f.
(Hint: For \(y \in \text { Range } f, y=f(x)=\frac{x}{x+2}\) for some x in [-1,1]
\(x=\frac{2 y}{(1-y)}\)
Answer:

Question 7.
Consider f : R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
Answer:

![]()
Question 8.
Consider f : R+ → [4, ∞) given by f(x) = x2 + 4. Show that f is invertible with the
inverse f-1 of/given by \(f^{-1}(y)=\sqrt{y-4}\) . where R+ is the set of ail non-negative real numbers.
Answer:

Question 9.
Consider f : R+ → [- 5, ∞) given by f (x) = 9x3 + 6x – 5. Show that f is invertible with
\(f^{-1}(y)=\left(\frac{(\sqrt{y+6}) \cdot 1}{3}\right)\)
Answer:

Question 10.
Let f : X → Y be an invertible function. Show that f has unique inverse. (Hint: suppose g1, and g2 are two inverses of f. Then for all y ∈ Y, fog1(y) as 1Y(y) = fog2(y). Use one-one ness of A
Answer:
Let g1 and g2 are two inverse of f, then for all y ∈ y
fog1 (y) = f [g (y)] = y = Iy (y)
fog2 (y) = f [g2 (y)] = y = Iy (y)
(fog1) (y) = (fog2) (y) ∀ y ∈ y
f(g1,(y)) = f (g2 (y)) ∀ y ∈ y
∴ g, (y) = g2 (y) (∴ f is one-one)
g1 =g2
⇒ Inverse of f is unique.
Question 11.
Consider f : {1, 2, 3} → {a, b, c} given by f(1) = a,f (2) = b and f(3) = Find f-1 and show that
(f -1)-1 = f
Answer:
Given that
f = {(1. a), (2, b), (3, c)}
f is one-one and onto
∴ f is invertible f-1 (a) = 1, f (b) = 2, f-1 (c) = 3,
∴ f1 (a, b, c} ⇒ {1,2, 3} is also one and onto
∵ Inverse of f is (f)-1 exist
(f1)-1 = {(1. a), (2, b), (3, c)}=f hence (f-1)-1 = f.
![]()
Question 12.
Let f : X → Y be an invertible function. Show that the inverse of f-1 is f, i.e., that (f -1)-1 = f
Answer:
Let f : X → Y is invertible
⇒ f is one and onto and
f-1 : Y ⇒ X is defined as f-1(y) = x
y : f (x) ∀ x ∈ X and y ∈ Y
let y1,y2 ∈ y
f-1 (y1) = f-2(y2)
fof1 (y1) = fof1 (y2)
Iy (y1) = Iy(y2)
⇒ y1 = y2 ∴ f1 is one-one
∀ x ∈ X, ∋ y ∈ Y such that
f1 (y) = x, hence f1 is onto
hence invertible.
let g = (f1)-1
gof-1 = Iy and f-1og = lx
∀ x ∈ X, Ix (x) = x
fof-1(x) = f-1 [g(x)] = x
fof-1 [g (x)] = f (x)
(fof-1) (g (x)) = f (x)
g (x) = f (x)
g = f
(f-1)-1 = f.
Question 13.
If f: R → R be given by \(f(x)=\left(3-x^{3}\right)^{\frac{1}{3}}\),then fof (x) is
(A)\(x^{\frac{1}{3}}\)
(B) x3
(C) x
(D) (3 – x3)
Answer:

![]()
Question 14.
Let \(f: \mathbf{R}-\left\{-\frac{4}{3}\right\} \rightarrow \mathbf{R}\),be a function as \(f(x)=+\frac{4 x}{3 x+4}\).The inverse off is the mag g : Range
\(f \rightarrow \mathbf{R}-\left\{-\frac{4}{3}\right\}\) given by
(A) \(g(y)=\frac{3 y}{3-4 y}\)
(B) \(g(y)=\frac{4 y}{4-3 y}\)
(C) \(g(y)=\frac{4 y}{3-4 y}\)
(D) \(g(y)=\frac{3 y}{4-3 y}\)
Answer: