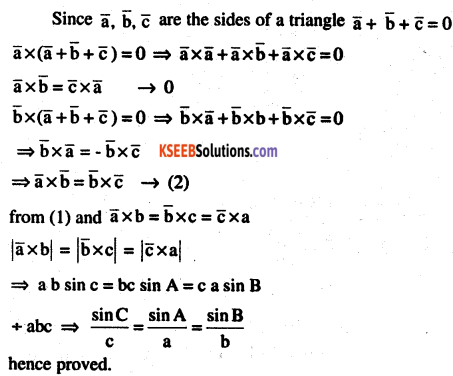2nd PUC Maths Question Bank Chapter 10 Vector Algebra Miscellaneous Exercise

Students can Download Maths Chapter 10 Vector Algebra Miscellaneous Exercise Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Maths Question Bank Chapter 10 Vector Algebra Miscellaneous Exercise

Question 1.
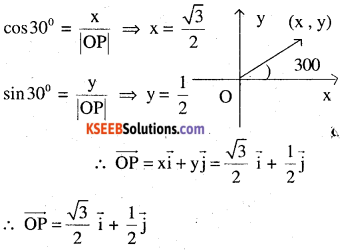
Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of x-axis.
Answer:
Let OP be the required vector

Question 2.
Find the scalar components and magnitude of the vector joining the points P(x_1,y₁,z₁) and Q (x₂, y₂, z₂).
Answer:

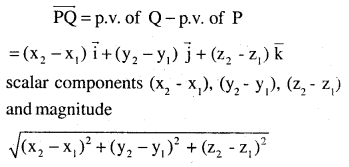
Question 3.
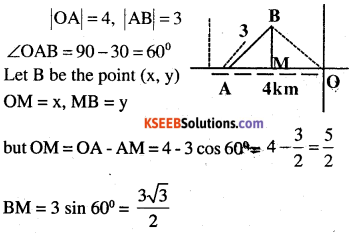
A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure.
Answer:

Question 4.
\(\overrightarrow{\mathbf{a}}=\overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}}, \text { then is it true that }|\overrightarrow{\mathbf{a}}|=|\overrightarrow{\mathbf{b}}|+|\overrightarrow{\mathbf{c}}|\) justify your answer.
Answer:

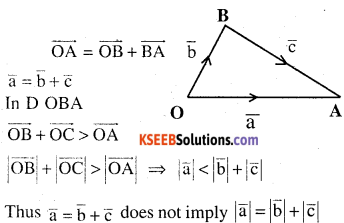
Question 5.
Find the value of x for which \(\mathbf{x}(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}) \)is a unit vector.
Answer:

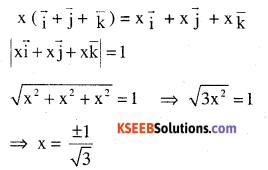
Question 6.
Find a vector of magnitude 5 units, and parallel to the resultant of the vectors
\(\overrightarrow{\mathrm{a}}=2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-\hat{\mathrm{k}} \text { and } \overrightarrow{\mathrm{b}}=\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+\hat{\mathrm{k}}\)
Answer:

Question 7.
If\(\overrightarrow{\mathrm{a}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}, \overrightarrow{\mathbf{b}}=2 \hat{\mathbf{i}}-\hat{\mathbf{j}}+3 \hat{\mathbf{k}} \text { and }\) and \(\overrightarrow{\mathbf{c}}=\hat{\mathbf{i}}-2 \hat{\mathbf{j}}+\hat{\mathbf{k}}\)find a unit vector parellel to the vector
\(2 \vec{a}-\vec{b}+3 \vec{c}\)
Answer:

Question 8.
Show that the points A(1, – 2, – 8), B (5, 0, – 2) and C (11, 3, 7) are collinear, and find the ratio in which B divides AC.
Answer:

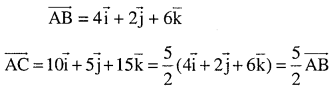
∴ hence AC and AB are coimear. Since A s
common A, B, C arc collinear
Let B divide AC in the ratio k: I

Question 9.
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are (2a + b) and \((\vec{a}-3 \vec{b})\)externally in the ratio 1:2. Also, show that P is the mid point of the line segment RQ.
Answer:

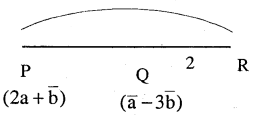
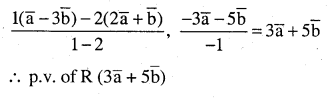
Question 10.
The two adjacent sides of a parallelogram are \(2 \hat{\mathbf{i}}-4 \hat{\mathbf{j}}+5 \hat{\mathbf{k}} \text { and } \hat{\mathbf{i}}-2 \hat{\mathbf{j}}-3 \hat{\mathbf{k}}\) .Find the unit vector parallel to its diagonal. Also,find its area.
Answer:

Question 11.
Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ
\(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\)
Answer:

Question 12.
Let \(\overrightarrow{\mathrm{a}}=\hat{\mathbf{i}}+4 \hat{\mathbf{j}}+2 \hat{\mathbf{k}}, \overrightarrow{\mathbf{b}}=3 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}+7 \hat{\mathbf{k}} \text { and }\overrightarrow{\mathrm{c}}=2 \hat{\mathrm{i}}-\hat{\mathrm{j}}+4 \hat{\mathrm{k}}\) .find the vector \(\overrightarrow{\mathrm{d}}\) which is perpendicular to both \(\overrightarrow{\mathbf{a}} \text { and } \overrightarrow{\mathbf{b}} \text { and } \overrightarrow{\mathbf{c}} . \overrightarrow{\mathbf{d}}\) = 15
Answer:

Question 13.
The scalar product of the vector \(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}\) a unit vector along the sum of vectors \(2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}-5 \hat{\mathbf{k}} \text { and } \quad \lambda \hat{\mathbf{i}}+2 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}\) is equal to ane. find the value of λ.
Answer:

Question 14.
If \(\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}\) are mutually perpendicular vectors of equal magnitudes, show that the vector is equally inclined to \(\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}\)
Answer:

Question 15.
Prove that
\((\overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}}) \cdot(\overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}})=|\overrightarrow{\mathbf{a}}|^{2}+|\overrightarrow{\mathbf{b}}|^{2}\) if and only if \(\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}\) are perpendicular ,givens \(\overrightarrow{\mathrm{a}} \neq \overrightarrow{0}, \overrightarrow{\mathrm{b}} \neq \overrightarrow{0}\)
Answer:

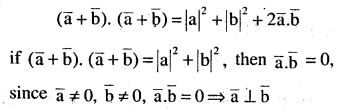
Choose the correct answer in Exercises 16 to 19.

Question 16.
If θ is the angle between two vectors \(\overrightarrow { { a } } \) and \(\overrightarrow { { b } } \), then 3.6 > 0 only when then \(\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}} \geq \mathbf{0}\) only when
(A)\(0<\theta<\frac{\pi}{2}\)
(B)\(0 \leq \theta \leq \frac{\pi}{2}\)
(C) 0<θ<π
(D) 0≤θ≤π
Answer:

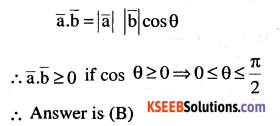
Question 17.
let \(\overrightarrow{\mathbf{a}} \text { and } \overrightarrow{\mathbf{b}}\) be two unit vector and θ is the angle between them. Then 3 + b is a unit vector if

Answer:

Question 18.
The value\(\hat{\mathbf{i}} \cdot(\hat{\mathbf{j}} \times \hat{\mathbf{k}})+\hat{\mathbf{j}} \cdot(\hat{\mathbf{i}} \times \hat{\mathbf{k}})+\hat{\mathbf{k}} \cdot(\hat{\mathbf{i}} \times \hat{\mathbf{j}})\)
(A) 0
(B) -1
(C) 1
(D) 3
Answer:

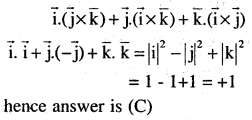
Question 19.
If θ is the angle between any two vectors \(\overrightarrow{\mathbf{a}} \text { and } \overrightarrow{\mathbf{b}}, \text { then }|\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}|=|\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}| \)when θ is equal to
(A) 0
(B) \(\frac{\pi}{4}\)
(C) \(\frac{\pi}{2}\)
(D) π
Answer:

2nd PUC Maths Vector Algebra Miscellaneous Exercise Extra Questions and Answers

Question 1.
Write a vector of magnitude 9 units in the direction of vector \(-2 \hat{\mathbf{i}}+\hat{\mathbf{j}}+2 \hat{\mathbf{k}}\) (CBSE 2019)
Answer:

Question 2.
find
\(\lambda \text { if }(2 i+6 j+4 k) \times(i-\lambda j+7 k)=0\)(CBSE 2010)
Answer:

Question 3.
If \(\overline{\mathbf{a}} \text { and } \overline{\mathbf{b}}\) are two vectors such that \(|\overline{\mathbf{a}} \cdot \overline{\mathbf{b}}|=|\overline{\mathbf{a}} \times \overline{\mathbf{b}}|\), what is the angle between \(\overline{\mathbf{a}} \text { and } \overline{\mathbf{b}}\)
Answer:

Question 4.
\(|\vec{a}|=\sqrt{3},|\vec{b}|=\frac{2}{3} \text { and } \vec{a} \times \vec{b}\)
is a vunit vector. Write the angle between \(\overline{\mathbf{a}} \text { and } \overline{\mathbf{b}}\) (CBSE 2010)
Answer:

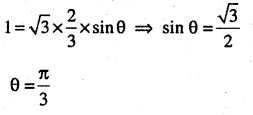
Question 5.
Write the projection of i – j on i + j (CBSE 2011)
Answer:

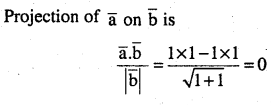
Question 6.
Write the value of \((\mathbf{i} \times \mathbf{j}) \cdot \overline{\mathbf{k}}+\mathbf{i} \cdot \mathbf{j}\)(CBSE 2012)
Answer:

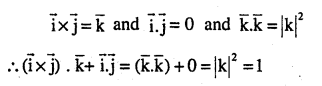
Question 7.
Find the scalar components of the vector \(\overrightarrow{\mathbf{A B}}\) with initial point A (2,1) and terminal point (-5,7).     (CBSE 2012)
Answer:

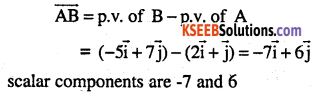
Question 8.
\(\bar { a } =\vec { i } +4\vec { j } +2\vec { k } ,\quad \bar { b } =3\vec { i } -2\vec { j } +7\bar { k } ,\bar { c } =3\vec { i } -\vec { j } +4\bar { k } \) .find a vector \(\overline{\mathbf{p}}\) which is perpendicular both \(\overline{\mathbf{a}} \text { and } \overline{\mathbf{b}} \text { and } \overline{\mathbf{p}} . \overline{\mathbf{c}}=18\)
Answer:

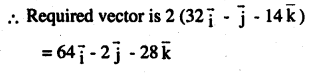
Question 9.
If \(\overline { { a } } =\overrightarrow { { i } } +\overrightarrow { { j } } +\overline { { k } } ,\quad \overline { { b } } =4\overrightarrow { { i } } -2\overrightarrow { { j } } +3\overline { { k } } ,\overline { { c } } =\overrightarrow { { i } } -2\overrightarrow { { j } } +\overline { { k } } \),find a vector of magnitude 6 units which is parallel to the vector \(2\overline { { a } } -\overline { b } +\overline { { 3c } } \)
Answer:

Question 10.
\(\overline { { a } } =\overrightarrow { { i } } +4\overrightarrow { { j } } +2\overline { { k } } ,\quad \overline { { b } } =3\overrightarrow { { i } } -2\overrightarrow { { j } } +7\overline { { k } } ,\overline { { c } } =2\overrightarrow { { i } } -\overrightarrow { { j } } +4\overline { { k } } \). find a vector d such that it is perpendiular to both \(\overline{\mathbf{a}} \text { and } \overline{\mathbf{b}} \text { and }\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{d}}=18\)
Answer:

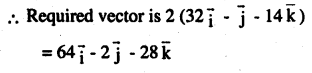
Question 11.
Using vectors find the area of the triangle with vectors A (1, 1, 2) , B (2, 3, 5), C(1, 5, 5) .   (CBSE 2011)
Answer:

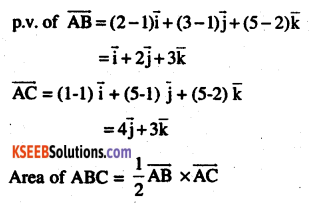
Question 12.
\(\alpha=3 i – j, \bar{\beta}=2 i+j-3 \bar{k}\) Express β in the form the form
β = β₁ + β₂ where β₁|| α and β₂ ⊥α (CBSE 2012)
Answer:

Question 13.
\(\begin{aligned}&\overline{\mathbf{a}} \times \overline{\mathbf{b}}=\overline{\mathbf{c}} \times \overline{\mathbf{d}}, \quad \overline{\mathbf{a}} \times \overline{\mathbf{c}}=\overline{\mathbf{b}} \times \overline{\mathbf{d}} \text { Show that }\\&(\overline{\mathbf{a}}-\overline{\mathbf{d}}) \| \mathbf{t} \mathbf{o}-\overline{\mathbf{c}} \text { when } \overline{\mathbf{a}} \neq \overline{\mathbf{d}} \text { and } \overline{\mathbf{b}} \neq \overline{\mathbf{c}}\end{aligned}\)(ISE 2011)
Answer:

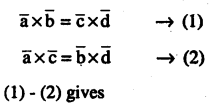
Question 14.
find
\(\overline{\mathbf{a}} \cdot \overline{\mathbf{b}} \text { of }|\overline{\mathbf{a}}|=\mathbf{3},|\overline{\mathbf{b}}|=\mathbf{4},|\overline{\mathbf{a}} \times \mathbf{b}|=6\) (CBSE 2009)
Answer:

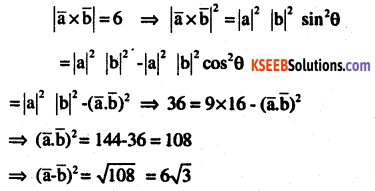
Question 15.
If \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) represent the sides of Δ show that \(\overline{\mathbf{a}} \times \overline{\mathbf{b}}=\overline{\mathbf{b}} \times \overline{\mathbf{c}}=\overline{\mathbf{c}} \times \overline{\mathbf{a}}\) hence derive sine formula. (CBSE 2008)
Answer: