2nd PUC Maths Question Bank Chapter 11 Three Dimensional Geometry Ex 11.2

Students can Download Maths Chapter 11 Three Dimensional Geometry Ex 11.2 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Maths Question Bank Chapter 11 Three Dimensional Geometry Ex 11.2

2nd PUC Maths Three Dimensional Geometry NCERT Text Book Questions and Answers Ex 11.2

Question 1
Show that the three lines with direction cosines
\(\frac{12}{13}, \frac{-3}{13}, \frac{-4}{13} ; \frac{4}{13}, \frac{12}{13}, \frac{3}{13} ; \frac{3}{13}, \frac{-4}{13}, \frac{12}{13}\) are mutually perpendicular
Answer:
Let the Directions cosines given for lines L₁, L₂ and L₃.
Let α be the angle between L₁, and L₂

similarly for L₂ and L₃ and L₃ and L₁ are perpendicular.

Question 2.
Show that the line through the points (1, -1, 2), (3, 4, -2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Answer:
Let A (1, -1, 2), B (3, 4, -2), C (0, 3, 2), D (3, 5, 6)
Dr’ of AB = (2,5,-4)
Dr’of CD = (3,2, 4)
a₁a₂ + b₁b₂ + C₁C₂ = 2 x 3 + 5 x 2+-4 x 4 = 0
hence the lines are perpendicular.

Question 3.
Show that the line through the points (4,7, 8), (2, 3, 4) is parallel to the line through the points (- 1, – 2, 1), (1, 2, 5).
Answer:
A (4,7,8), B (2,3,4), C (-1, -2,1), D (1,2,5)
Dr’ of AB (2-4,3-7,4-8), (-2, -4, -4)
Dr’ of CD (1+1, 2+2, 5-1) (2,4,4)
since Dr’ of AB and Dr’ of CD are proportional
\(\frac{-2}{2}=\frac{-4}{4}=\frac{-4}{4} \quad \mathrm{AB} \| \mathrm{CD}\)

Question 4.
Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector \(3 \hat{\mathbf{i}}+2 \hat{\mathbf{j}}-2 \hat{\mathbf{k}}\)
Answer:

Question 5.
Find the equation of the line in vector and in cartesian form that passes through the point with position vector \(2 \hat{\mathbf{i}}-\hat{\mathbf{j}}+4 \hat{\mathbf{k}}\) and is in the direction \(\hat{\mathbf{i}}+2 \hat{\mathbf{j}}-\hat{\mathbf{k}}\)
Answer:
Let \(\bar{a}=2 i-j+4 \bar{k} \text { and } \bar{b}=i+2 j-\bar{k}\)
Required vector equation is \(\overline{\mathbf{r}}=\overline{\mathbf{a}}+\lambda \overline{\mathbf{b}}\)

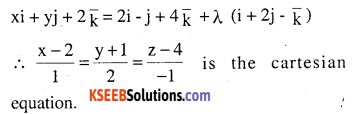
Question 6.
Find the cartesian equation of the line which passes through the point (- 2, 4, – 5) and parallel to the line given by
\(\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}\)
Answer:
\(\bar{a}=-2 i+4 j-5 \bar{k} \text { and } \bar{b}=3 i+5 j+6 \bar{k}\) equation of a line through (-2, 4, -5) and is parallel to the vector \(3 i+5 j+6 \bar{k}\)
\(\frac{x+2}{3}=\frac{y-4}{5}=\frac{z+5}{6}\)

Question 7.
The cartesian equation of a line is
\(\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}\) .
write its vector form.
Answer:
\(\bar{a}=5 i-4 j+6 \bar{k}, \bar{b}=3 i+7 j+2 \bar{k}\)
equation of a line through the point with p.v
\(5i-4j+6\bar { k } and\quad is\quad parallel\quad to\quad 3i+7j+2\bar { k } is\quad \overrightarrow { { r } } =(5{ i }-4{ j }+6\overline { { k } } )+\lambda (3{ i }+7{ j }+2\overline { { k } } )\)

Question 8.
Find the vector and the cartesian equations of the lines that passes through the origin and (5, – 2, 3).
Answer:
Equation of a line through two points is

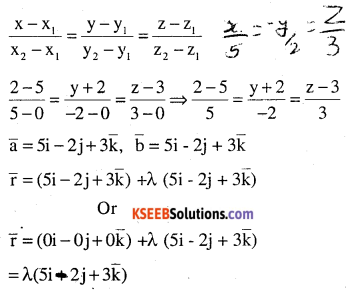
Question 9.
Find the vector and the cartesian equations of the line that passes through the points
(3, – 2, – 5), (3, – 2, 6).
Answer:

Question 10.
Find the angle between the following pairs of lines:
(i) \(\begin{aligned}&\overrightarrow{\mathbf{r}}=2 \hat{\mathbf{i}}-5\hat{\mathbf{j}}+\hat{\mathbf{k}}+\lambda(3 \hat{\mathbf{i}}+2 \hat{\mathbf{j}}+6 \hat{\mathbf{k}}) \text { and }\\&\overrightarrow{\mathbf{r}}=7 \hat{\mathbf{i}}-6 \hat{\mathbf{k}}+\mu(\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+2 \hat{\mathbf{k}})\end{aligned}\)
Answer:
The given lines are respectively parallel to
\(\overline{\mathrm{b}}_{1}=3 \mathrm{i}+2 \mathrm{j}+6 \overline{\mathrm{k}} \text { and } \mathrm{i}+2 \mathrm{j}+2\overline{\mathrm{k}}=\overline{\mathrm{b}}_{2}\)
Let θ be the angle between them

(ii) \(\overrightarrow{\mathbf{r}}=3 \hat{\mathbf{i}}+\hat{\mathbf{j}}-2 \hat{\mathbf{k}}+\lambda(\hat{\mathbf{i}}+\hat{\mathbf{j}}-2 \hat{\mathbf{k}}) \text {and }\overrightarrow{\mathbf{r}}=2 \hat{\mathbf{i}}-\hat{\mathbf{j}}-56\hat{\mathbf{k}}+\mu(3 \hat{\mathbf{i}}-5 \hat{\mathbf{j}}-4 \hat{\mathbf{k}})\)
Answer:
The given lines are respectively parallel to
\(\overline{\mathrm{b}}_{1}=\mathrm{i}-\mathrm{j} 2 \overline{\mathrm{k}} \text { and } \overline{\mathrm{b}}_{2}=3 \mathrm{i}-5 \mathrm{j}-4 \overline{\mathrm{k}}\)
Let θ be the angle between them

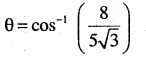
Question 11.
Find the angle between the following pair of lines:

(i) \(\frac{x-2}{2}=\frac{y-1}{5}=\frac{z+3}{-3} \text { and } \frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}\)
Answer:
The given lines are respectively parallel to
\(\overline{\mathrm{b}}_{1}=2 \mathrm{i}+5 \mathrm{j}-3 \overline{\mathrm{k}} \text { and } \overline{\mathrm{b}}_{2}=-\mathrm{i}+8 \mathrm{j}+4 \overline{\mathrm{k}}\)
Let θ be the angle between them

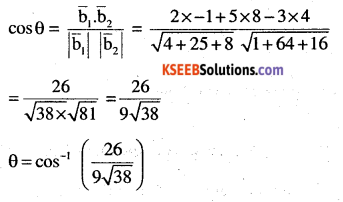
(ii) \(\frac{x}{2}=\frac{y}{2}=\frac{z}{1} \text { and } \frac{x-5}{4}=\frac{y-2}{1}=\frac{z-3}{8}\)
Answer:
Dr’ of lines are (2,2,1), {4,1,8}
Let θ be the angle between them

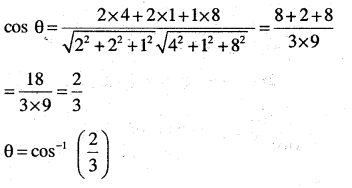
Question 12.
Find the values of p so that the lines 1-x
\(\frac{1-x}{3}=\frac{7 y-14}{2 p}=\frac{z-3}{2} \text { and }\frac{7-7 x}{3 p}=\frac{y-5}{1}=\frac{6-z}{5}\) are at right angles
Answer:

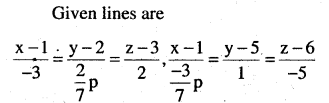
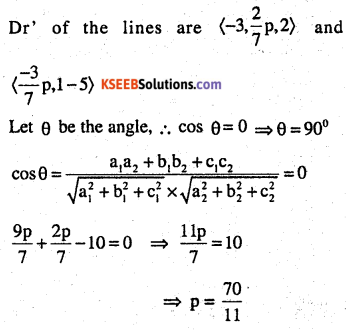
Question 13.
Show that the lines
\(\frac { x-5 }{ 7 } =\frac { y+2 }{ -5 } =\frac { z }{ 1 } { and } \quad \frac { x }{ 1 } =\frac { y }{ 2 } =\frac { z }{ 3 } \) are perpendicular to each other.
Answer:
Dr’s are (7,-5,1), and (1, 2,3)
a₁b₁ + a₂b₂  + a₃b₃
7 x 1- 5 x 2 + 1 x 3 ⇒ 10 – 10 = 0
The products of Dr’s are equal, lines are ‘⊥’

Question 14.
Find the shortest distance between the lines
\(\begin{aligned}&\overrightarrow{\mathbf{r}}=(\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+\hat{\mathbf{k}})+\lambda(\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}) \text { and }\\&\overrightarrow{\mathbf{r}}=2 \hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}+\mu(2 \hat{\mathbf{i}}+\hat{\mathbf{j}}+2 \hat{\mathbf{k}})\end{aligned}\)
Answer:

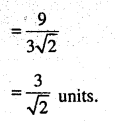
Question 15.
Find the shortest distance between the lines
\(\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1} \text { and } \frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}\)
Answer:

Question 16.
Find the shortest distance between the lines whose vector equations are
\(\begin{aligned}&\overrightarrow{\mathbf{r}}=(\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+3 \hat{\mathbf{k}})+\lambda(\hat{\mathbf{i}}-3 \hat{\mathbf{j}}+2 \hat{\mathbf{k}})\\&\text { and } \overrightarrow{\mathbf{r}}=(4 \hat{\mathbf{i}}+5 \hat{\mathbf{j}}+6 \hat{\mathbf{k}}+\mu(2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}+\hat{\mathbf{k}})\end{aligned}\)
Answer:

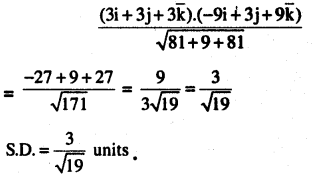
Question 17.
Find the shortest distance between the lines whose vector equations are
\(\begin{aligned}&\overrightarrow{\mathbf{r}}=(1-t) \hat{\mathbf{i}}+(t-2) \hat{\mathbf{j}}+(3-2 \mathbf{t}) \hat{\mathbf{k}} \text { and }\\&\overrightarrow{\mathbf{r}}=(\mathbf{s}+1) \hat{\mathbf{i}}+(2 \mathbf{s}-\mathbf{1}) \hat{\mathbf{j}}-(2 \mathbf{s}+\mathbf{1}) \hat{\mathbf{k}}\end{aligned}\)
Answer: