Students can Download Maths Chapter 13 Probability Ex 13.2 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 13 Probability Ex 13.2
2nd PUC Maths Probability NCERT Text Book Questions and Answers Ex 13.2
Question 1.
If \(\mathbf{P}(\mathbf{A})=\frac{3}{5} \text { and } \mathbf{P}(\mathbf{B})=\frac{1}{5}, \text { find } \mathbf{P}(\mathbf{A} \cap \mathbf{B})\) ,find P(A∩B) if A and B are independent events.
Answer:
If two events A and B are independents P (A∩B) = P(A). P(B)
\((A \cap B)=\frac{3}{5} \times \frac{1}{5}=\frac{3}{25}\)
Question 2.
Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.
Answer:
There are 26 black cards out 52 cards. When cards are drawn without replacement,
\(P(\text { both black cards })=\frac{26 \mathrm{C}_{2}}{52 \mathrm{C}_{2}}=\frac{26 \times 25}{52 \times 51}=\frac{25}{102}\)
![]()
Question 3.
A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale, otherwise, it is rejected. Find the probability that a box containing 15 oranges out of which 12 are good and 3 are bad ones will be approved for sale.
Answer:
Since selection is without replacement

Question 4.
A fair coin and an unbiased die are tossed.Let A be the event ‘head appears on the coin’ and B be the event ‘3 on the die’.Check whether A and B are independent events or not.
Answer:

Question 5.
A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event, ‘the number is event, and B be the event, ‘the number is red’. Are A and B independent?
Answer:
A : number is even, B : The number is red
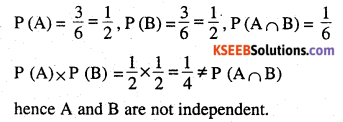
Question 6.
Let E and F be events with P(E) \({ P }({ E })=\frac { 3 }{ 5 } ,{ P }({ F })=\frac { 3 }{ 10 } { \quad and\quad }{ P }({ E }\cap { F })=\frac { 1 }{ 5 } \). Are E and F independent?
Answer:
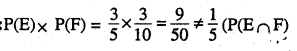
hence they are not independent.
![]()
Question 7.
Given that the events A and B are such that \(P(A)=\frac { 1 }{ 2 } ,P(A\cup B)=\frac { 3 }{ 5 } \quad { and }\quad P(B)=p\) Find p if they are
(i) mutually exclusive
(ii) independent.
Answer:
(i) If the events are mutually exclusive

Question 8.
Let A and B be independent events with
P(A) = 0.3 and P (B) = 0.4. Find
(i) P(A∩B)
(ii)P(A∪B)
(iii) P (A|B)
(iv) P (B|A)
Answer:

Question 9.
If A and B are two events such that
\(P(A)=\frac { 1 }{ 4 } ,{ P }({ B })=\frac { 1 }{ 2 } { and }{ P }({ A }\cap { B })=\frac { 1 }{ 8 } \)
Answer:

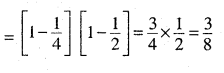
![]()
Question 10.
Events A and B are such that \({ P }({ E })=\frac { 3 }{ 5 } ,{ P }({ F })(B)=\frac { 7 }{ 12 } \) P (not A or not B) = \(\frac{1}{4}\). State whether A and B are independent ?
Answer:

Question 11.
Given two independent events A and B such that P (A) = 0.3, P (B) = 0.6. Find
(i) P (A and B)
Answer:
i.e. P (A∩B) = P (A) x P (B) = .3 x .6 = .18
(ii) P (A and not B)
Answer:
P(A and not B) = \(P(A \cap \bar{B})\)
= P(A) x \(P(\bar{B})\) ⇒ P (A) x [1-P(B)]
= .3 x (1 – 0.6) = .3 x .4 = .12
(iii) P (A or B)
Answer:
P (A or B) = P (A∪B)
= P (A) + P (B) – P (A∩B)
= .3+ .6-.18 = .9 -.18 = .72
(iv) P (neither A nor B)
Answer:
P (neither A nor B) = \(P(\bar{A} \cap \bar{B})\)
= \(P(\overline{A \cup B})\)
= 1 -P(A∪B)= 1 -.72 = .28
Question 12.
A die is tossed thrice. Find the probability of getting an odd number at least once.
Answer:
E : an odd number at least once
\(\overline{\mathrm{E}}\) : not an odd number
\(\overline{\mathrm{E}}\) : an even number on all times
we get even all time 3 x 3 x 3 = 27
\(P(E)=1-P(\bar{E})=1-\frac{27}{216}=\frac{7}{8}\)
![]()
Question 13.
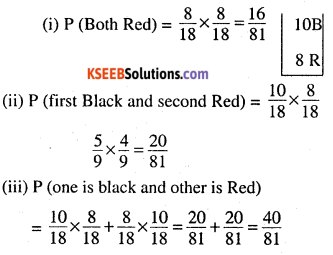
Two balls are drawn at random With replacement from a box containing 10 black and 8 red balls. Find the probability that
(i) both balls are red.
(ii) first ball is black and second is red
(iii) one of them is black and other is red
Answer:
Question 14.
Probability of solving specific problem independently by A and B are \(\frac{1}{2} \text { and } \frac{1}{3}\) respectively. If both try to solve the problem independently, find the probability that
(i) the problem is solved
(ii) exactly one of them solves the problem.
Answer:

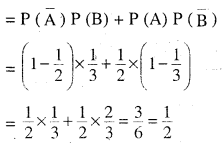
Question 15.
One card is drawn at random from a well shuffled deck of 52 cards. In which of the following cases are the events E and F independent ?
(i) E : ‘the card drawn is a spade’
F : ‘the card drawn is a ace’
(ii) E : ‘the card drawn is black’
F : ‘the card drawn is a king’
(iii) E : ‘the card drawn is a king or queen’
F : ‘the card drawn is a queen or jack’.
Answer:

![]()
Question 16.
In a hostel, 60% of the students read Hindi news paper, 40% read English news paper and 20% read both Hindi^and English news papers. A student is selected at random.
(a) Find the probability that she reads neither Hindi nor English news papers.
(b) If she reads Hindi news paper, find the probability that she reads English news paper.
(c) If she reads English news paper, find the probability that she reads Hindi news paper.
Answer:
(a) 20% read neither Hindi nor english

Choose the correct answer in Exercises 17 and 18.
Question 17.
The probability of obtaining an even prime number on each die, when a pair of dice is rolled is
(A) 0
(B) \(\frac{1}{3}\)
(C) \(\frac{1}{12}\)
(D) \(\frac{1}{36}\)
Answer:
Even Prime no is (2,2)
P (even prime no) = \(\frac{1}{36}\)
Option ‘D’
Question 18.
Two events A and B will be independent, if
(A) A and B are mutually exclusive
(B) P (A’B’) = [1 – P(A)] [1 – P(B)]
(C) P (A) = P (B)
(D) P (A) + P (B) = 1
Answer:
P(A’B’) = P(A’∩B’)
= \(P\bar { A\cup B } \)
= 1 – P (A∪B)
= 1 – P(A) – P(B) – P(A) – P(B)
= 1 – P (A) – P (B) (1 – P (A)]
= [1 – P (A)] [1 -P(B)
Option ‘B’