2nd PUC Maths Question Bank Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise

Students can Download Maths Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Maths Question Bank Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise

Find the value of the following:

Question 1.
\(\cos ^{-1}\left(\cos \frac{13 \pi}{6}\right)\)
Answer:

Question 2.
\(\tan ^{-1}\left(\tan \frac{7 \pi}{6}\right)\)
Answer:

Prove that

Question 3.
\(2 \sin ^{-1} \frac{3}{5}=\tan ^{-1} \frac{24}{7}\)
Answer:

Question 4.
\(\sin ^{-1} \frac{8}{17}+\sin ^{-1} \frac{3}{5}=\sin ^{-1} \frac{77}{85}\)
Answer:

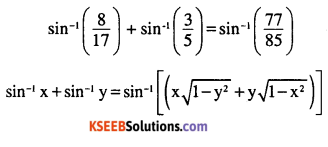
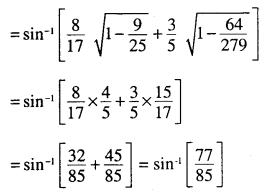
Question 5.
\(\cos ^{-1} \frac{4}{5}+\cos ^{-1} \frac{12}{13}=\cos ^{-1} \frac{33}{65}\)
Answer:

Question 6.
\(\cos ^{-1} \frac{12}{13}+\sin ^{-1} \frac{3}{5}=\sin ^{-1} \frac{56}{65}\)
Answer:

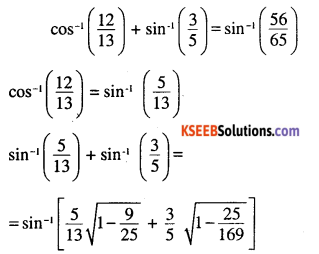
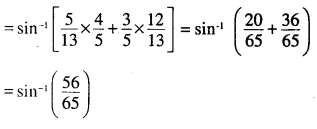
Question 7.
\(\tan ^{-1} \frac{63}{16}=\sin ^{-1} \frac{5}{13}+\cos ^{-1} \frac{3}{5}\)
Answer:

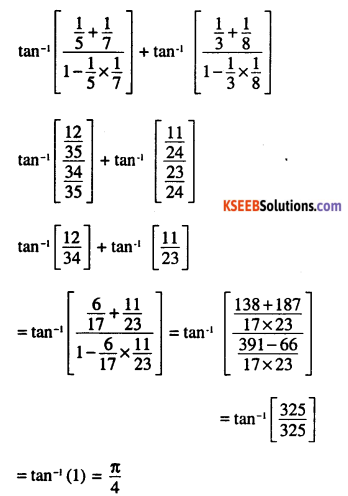
Question 8.
\(\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{7}+\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{8}=\frac{\pi}{4}\)
Answer:

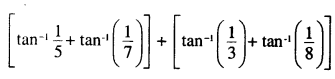
Prove that

Question 9.
\(\tan ^{-1} \sqrt{x}=\frac{1}{2} \cos ^{-1}\left(\frac{1-x}{1+x}\right), x \in[0,1]\)
Answer:

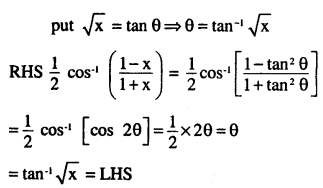
Question 10.
\(\cot ^{-1}\left(\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right)=\frac{x}{2}, x \in\left(0, \frac{\pi}{4}\right)\)
Answer:

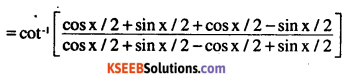
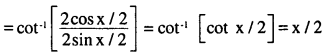
Question 11.
\(\begin{aligned}&\tan ^{-1}\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right)=\frac{x}{4}-\frac{1}{2} \cos ^{-1} x\\&-\frac{1}{\sqrt{2}} \leq x \leq[\text { Hint: put } x=\cos 2 \theta]\end{aligned}\)
Answer:

Question 12.
\(\frac{9 \pi}{8}-\frac{9}{4} \sin ^{-1} \frac{1}{3}=\frac{9}{4} \sin ^{-1} \frac{2 \sqrt{2}}{3}\)
Answer:

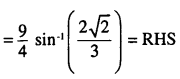
Question 13.
2 tan^-1 (cos x) = tan^-1 (2cosec x)
Answer:

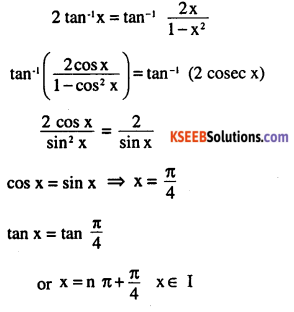
Question 14.
\(\tan ^{-1} \frac{1-x}{1+x}=\frac{1}{2} \tan ^{-1} x,(x>0)\)
Answer:


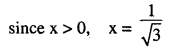
Choose the correct Answer

Question 15.
\(\sin \left(\tan ^{-1} x\right),|x|<1 \text { is equal to }\)
(A) \(1, \frac{1}{2}\)
[B] \(1, \frac{1}{2}\)
(C) 0
(D)\(\frac{1}{2}\)
Answer:

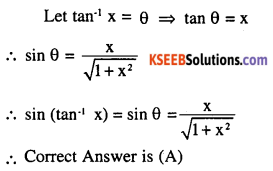
Question 16.
\(\sin ^{-1}(1-x)-2 \sin ^{-1} x=\cfrac{\pi}{2}, \text { then } x\)
(A) \(0, \frac{1}{2}\)
[B] \(1, \frac{1}{2}\)
(C) 0
(D)\(\frac{1}{2}\)
Answer:

Question 17.
\(\tan ^{-1}\left(\cfrac{x}{y}\right)-\tan ^{-1} \cfrac{x-y}{x+y} \text { is equal to }\)
(A)\(\frac{\pi}{2}\)
(B)\(\frac{\pi}{3}\)
(C)\(\frac{\pi}{4}\)
(D)\(\frac{-3 \pi}{4}\)
Answer:

2nd PUC Maths Inverse Trigonometric Functions Miscellaneous Exercise Additional Questions and Answers

Multiple Choice Questions:

Question 1.
cos^-1 cos(x) = x, then x lies in the interval
(a) [0,π]
(b) \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
(c) (o,π])
(d) \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
Answer:
(a) [0,π]

Question 2.
\(\cos ^{-1} \cos \left(\cfrac{4 \pi}{3}\right)=\)
(a) \(\frac{4 \pi}{3}\)
(b) \(\frac{2 \pi}{3}\)
(c) \(\frac{-\pi}{3}\)
(d) – π
Answer:

Question 3.
\(\sin ^{-1}\left(\cfrac{4}{5}\right)-\sec ^{-1}\left(\cfrac{5}{4}\right)=\sin ^{-1}\left(\cfrac{4}{5}\right)+\cos ^{-1}\left(\cfrac{4}{5}\right)\)
(a) \(\frac{\pi}{2}\)
(b) 0
(c) π
(d) \(\frac{-\pi}{4}\)
Answer:
(a) sin¹ x + cos^-1 x = \(\frac{\pi}{2}\)

Question 4.
\(\left(\sqrt[12]{(2 x-2)}\left(\cfrac{-1}{3}\right)\right)+(-\sin x\)
Answer:
(a) \(\frac{24}{25}\)
(b) \(-\frac{24}{25}\)
(c) \(-\frac{6}{25}\)
(d) \(\frac{-6}{25}\)
Answer: (b)

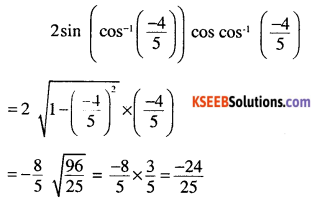
Question 5.
The value of tan^-1 (tan 5)
(a) 2π
(b) 5 – 2π
(c) 5
(d) \(\frac{2 \pi}{3}\)
Answer:
(b).
Let 2π – 5 = θ,
⇒ 5 = 2π – θ
tan 5 = tan (2π – θ)
tan^-1 (tan 5) = tan^-1 tan (2π – θ)
= tan^-1 [-tan θ]
= tan^-1 [tan (-θ)] = – θ
= – (2π – 5) = 5 – 2π

Question 6.
If a > b > c,
\(\cot ^{-1}\left(\cfrac{1+a b}{a-b}\right)+\cot ^{-1}\left(\cfrac{1+b c}{b-c}\right)+\cot ^{-1}\left(\cfrac{1+a c}{c-a}\right)\)
(a) 0
(b) π
(c) 2π
(d) \(\frac{\pi}{2}\)
Answer:

2nd PUC Maths Inverse Trigonometric Functions Miscellaneous Exercise Extra Question and Answers

Question 1.
Find
\(\sin ^{-1} \sin \left(\cfrac{3 \pi}{5}\right)\) (CBSE 2010)
Answer:

Question 2.
Find the principle value of \(^{\cot ^{-1}}\left(\cfrac{-1}{\sqrt{3}}\right)\)
Answer:

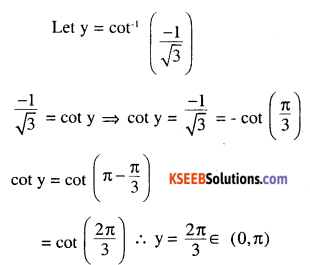
Question 3.
Write \(\cot ^{-1}\left(\cfrac{1}{\sqrt{x^{2}-1}}\right),|x|>1\) in the simplest form
Answer:

Question 4.
Show that \(\sin ^{-1}(2 x \sqrt{1-x^{2}}\}=2 \sin ^{-1} x\)
Answer:

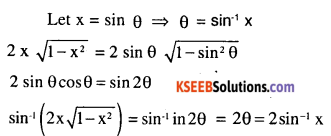
Question 5.
Find the value of tan (tan^-1 x + cot^-1 x)
Answer:

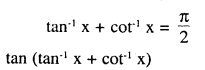
Question 6.
Solve \(\tan ^{-1}\left\{\cfrac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}\right\}\) (CBSE 09)
Answer:

Question 7.
Prove that \(\tan ^{-1} x+\tan ^{-1} \cfrac{2 x}{1-x^{2}}=\tan ^{-1}\left(\cfrac{3 x-x^{3}}{1-3 x^{2}}\right)\)
Answer: