2nd PUC Maths Question Bank Chapter 3 Matrices Miscellaneous Exercise

Students can Download Maths Chapter 3 Matrices Miscellaneous Exercise Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Maths Question Bank Chapter 3 Matrices Miscellaneous Exercise

Question 1.
Let \(A=\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}\), Show that (al +bA)ⁿ + na^{n – 1} ba where 1 is the identity matrix of order 2 and n ∈ N.
Answer:

Question 2.
If\(A=\left[\begin{array}{lll}{1} & {1} & {1} \\{1} & {1} & {1} \\{1} & {1} & {1}\end{array}\right]\)
,prove that
Aⁿ = \(\left[\begin{array}{lll}{3^{n-1}} & {3^{n-1}} & {3^{n-1}} \\{3^{n-1}} & {3^{n-1}} & {3^{-1}} \\{3^{n-1}} & {3^{n-1}} & {3^{n-1}}\end{array}\right], n \in N\)
Answer:

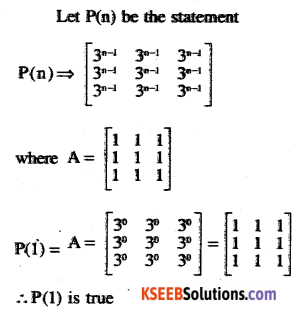
Question 3.
\(\mathbf{A}=\left[\begin{array}{ll}{\mathbf{3}} & {-4} \\{\mathbf{1}} & {\mathbf{1}}\end{array}\right]\)
then prove that
Aⁿ = \(\left[\begin{array}{cc}{1+2 n} & {-4 n} \\{n} & {1-2 n}\end{array}\right]\) where n is any positive integer.
Answer:

∴ P (k +1) is true
P(n) is true for all the values of +ve n.

Question 4.
If A and B are symmetric matrices, prove that AB – BA is a skew symmetric matrix.
Answer:
Since A &B are symmetric matrices A = a’ & B = B’
To prove (AB – BA)’ = – (AB – BA)
L.H.S = (AB – BA)’
(AB)’ – (BA)’
= B’A’-A’B’
= BA – AB
= – (AB – BA) = R.H.S
Thus proved.

Question 5.
Show that the matrix g’AB is symmetric or skew symmetric according as A is symmetric or skew symmetric.
Answer:

Question 6.
find the values of x, y, z if the matrix
A = \(\left[\begin{array}{rrr}{0} & {2 y} & {x} \\{x} & {y} & {-z} \\{x} & {-y} & {z}\end{array}\right]\) satisfy the equation A’ A = 1
Answer:

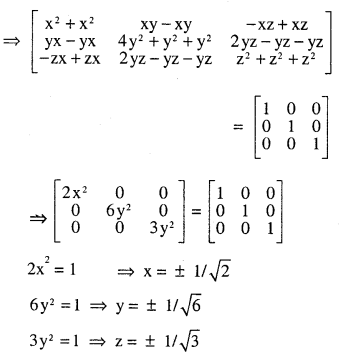
Question 7.
For what values of x:
\(\left[\begin{array}{lll}{1} & {2} & {1}\end{array}\right]\left[\begin{array}{rrr}{1} & {2} & {0} \\{2} & {0} & {1} \\{1} & {0} & {2}\end{array}\right]\left[\begin{array}{l}{0} \\{2} \\{x}\end{array}\right]=0 ?\)
Answer:

Question 8.
\(\mathbf{A}=\left[\begin{array}{rr}{3} & {1} \\{-1} & {2}\end{array}\right]\) show that A² – 5A + 7I = 0
Answer:

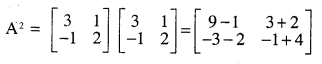
Question 9.
Find x, if
\(\left[\begin{array}{ccc}{\mathbf{x}} & {-5} & {-1}\end{array}\right]\left[\begin{array}{ccc}{\mathbf{1}} & {\mathbf{0}} & {\mathbf{2}} \\{\mathbf{0}} & {\mathbf{2}} &{\mathbf{1}} \\{\mathbf{2}} & {\mathbf{0}} &{\mathbf{3}}\end{array}\right]\left[\begin{array}{l}{\mathbf{x}} \\{\mathbf{4}} \\ {\mathbf{1}}\end{array}\right]=\mathbf{0}\)
Answer:

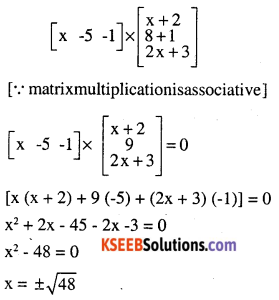
Question 10.
A manufacturer produces three products x, y, z which he sells in two markets. Annual sales are indicated below:

(a) If unit sale prices of, y and z are ₹2. 50, ₹1.50 and ₹1.00, respectively, find the total revenue in each market with the help of matrix algebra.
(b) If the costs of the above three commodities are ₹ 2.00, ₹ 1.00 and 50 paise respectively. Find the gross profit.
Answer:
Matrix representing the sales is

Profit in market I is
₹ 46,000 – ₹ 31,000
= ₹ 15,000

Profit in market 11 is
₹ 53,000 – ₹36,000
= ₹ 17,000

Gross profit
= ₹ 15,000 + ₹17,000
= ₹ 32,000.

Question 11.
Find the matrix X so that
\(\mathbf{X}\left[\begin{array}{lll}{1} & {2} & {3} \\{4} & {5} & {6}\end{array}\right]_{2 \times 3}=\left[\begin{array}{rrr}{-7} & {-8} & {-9} \\{2} & {4} & {6}\end{array}\right]_{2 \times 3}\)
Answer:

Question 12.
If A and B are square matrices of the same order such that AB = BA, then prove by induction that ABⁿ = BⁿA. Further, prove that (AB)ⁿ = Aⁿ Bⁿ for all n ∈ N.
Answer:
(i) Let P(n) be the statement
P(n) – ⇒ Ab ⁿ = BⁿA
P(1) ⇒ AB = BA
∴ P( 1) is true
Let P(k) be true
P(k) ⇒ AB^k = B^kA
P(k +1) ⇒ AB^k+1
= A(B^kB) = (AB^k)B
∵ matrix multiplication is associative.
⇒ (B^kA) B ⇒ B^k (AB) = B^k (BA)
= (B^kB) A = B^k+1 A
Hence P(k + 1) is true.
∴ P(n) is true for all the values of n ∈ N

(ii) Let P(n) be the statement
P(n) ⇒ (AB)ⁿ = AⁿBⁿ
P(1) = (AB)¹ = AB
∴ P(1) is true Let P(k) be true
P(k) ⇒ (AB)^k
= A^kB^k P(k+1)
⇒ (AB)^k+1 = (AB)^kAB = (A^kB^k) AB
= A^k (B^kA)B = A^k (AB^k) B
(∵ ABⁿ = BⁿA whenever Ab = BA)
_{= A}k+1 _Bk+1
∴ P (k+1) is true
Hence P(n) is true for all the natures of n ∈ N

Choose correct answer in the following questions:

Question 13.
If \(\mathbf{A}=\left[\begin{array}{ll}{\alpha} & {\beta} \\{\gamma} & {-\alpha}\end{array}\right]\)
is such that A²= I ,then
(A) \(1+\alpha^{2}+\beta \gamma=0\)
(B) \(1-\alpha^{2}+\beta \gamma=0\)
(C) \(1-\alpha^{2}-\beta \gamma=0\)
(D) \(1+\alpha^{2}-\beta \gamma=0\)
Answer:

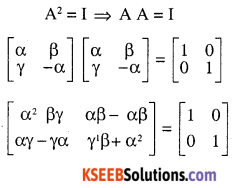
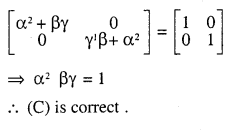
Question 14.
If the matrix A is both symmetric and skew symmetric, then
(A) A is a diagonal martix
(B) A is a zero matrix
(C) A is a square matrix
(D) None of these
Answer:
Let A be a square matrix such that A is both symmetric & skew-symmetric
⇒ A’ = A – (i) & A’ = – A -(ii)
⇒ A + A = 0  from (i) & (ii)
2A = 0
⇒ A = o
∴ (b) is correct

Question 15.
If A is square matrix such that A² = A, then (I + A)³ – 7A is equal to
(A) A
(B) I – A
(C) I
(D) 3A
Answer:
A² = A
(I + A)³ – 7A = (I + A) (I+A)² – 7A
= (I + A) {(I + A) (I+A)} -7A
= (I + A) (I² + 2A+A²) – 7A
[v IA = AI = A]
= (I + A) (I+2A+A) – 7A (A²= A)
= (I + A) (I + 3A) – 7A
= I² + AI + 3IA + 3A² – 7A
= I + A + 3A + 3A – 7A
[∵ A² = A & IA = AI = A]
=1
∴ (C) is correct.

2nd PUC Maths Matrices Miscellaneous Exercise Additional Questions and Answers

One Mark Questions:

Question 1.
If \(\mathbf{A}=\left(\begin{array}{ll}{\mathbf{0}} & {\mathbf{1}} \\{\mathbf{1}} & {\mathbf{0}}\end{array}\right), \mathbf{F} \text { ind } \mathbf{A}^{4}\)
(UP CET 2010)
Answer:

Question 2.
If
\(\mathbf{A}=\left(\begin{array}{rr}{0} & {2} \\{3} & {-4}\end{array}\right), \mathbf{K A}=\left(\begin{array}{ll}{0} & {3 \mathbf{a}} \\{2 \mathbf{b}} & {24}\end{array}\right)\),find k, a and b.
Answer

Question 3.
Find X and Y
\(2 \mathbf{X}-\mathbf{Y}=\left[\begin{array}{rrr}{6} & {-6} & {0} \\{-4} & {2} & {1} \end{array}\right]\)
\(\mathbf{X}+2 \mathbf{Y}=\left[\begin{array}{rrr}{3} & {2} & {5} \\{-2} & {1} & {-7}\end{array}\right]\)
Answer:

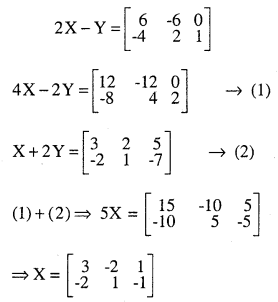
Question 4.
\(\left[\begin{array}{rrr}{1} & {1} & {1} \\{1} & {-2} & {-2} \\{1} & {3} &{2}\end{array}\right]\left[\begin{array}{l}{x} \\{y} \\{z}\end{array}\right]=\left[\begin{array}{l}{0} \\{3} \\{4}\end{array}\right], \text { then }\left[\begin{array}{l}{x} \\{y} \\{z}\end{array}\right]\)(I I T 2006)
Answer:

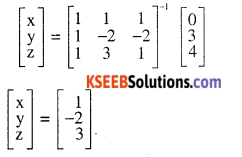
Question 5.
\(\mathbf{A}=\left[\begin{array}{lll}{6} & {8} & {7} \\{4} & {2} & {3} \\{9} & {7} & {1}\end{array}\right]\)
is the sum of symmentric and skew symmentric matrix, Find B
Answer: