2nd PUC Maths Question Bank Chapter 4 Determinants Miscellaneous Exercise

Students can Download Maths Chapter 4 Determinants Miscellaneous Exercise Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

karnataka 2nd PUC Maths Question Bank Chapter 4 Determinants Miscellaneous Exercise

Question 1.
Prove that the determinant
\(\left| \begin{array}{rrr} { x } & { \sin \theta } & { \cos \theta } \\ { -\sin \theta } & { -x } & { 1 } \\ { 1 } & { 1 } & x \end{array} \right| is\quad independent\quad of\quad \theta \)
Answer:

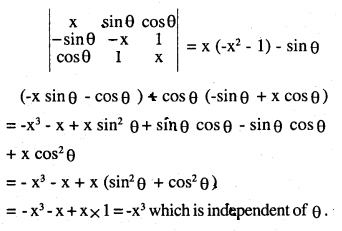
Question 2.
With out expanding, prove that
\(\left|\begin{array}{lll}{\mathbf{a}} & {\mathbf{a}^{2}} & {\mathbf{b} \mathbf{c}} \\{\mathbf{b}} & {\mathbf{b}^{2}} & {\mathbf{c} \mathbf{a}} \\{\mathbf{c}} & {\mathbf{c}^{2}} & {\mathbf{a} \mathbf{b}}\end{array}\right|=\left|\begin{array}{ccc}{\mathbf{1}} & {\mathbf{a}^{2}} & {\mathbf{a}^{3}} \\{\mathbf{1}} & {\mathbf{b}^{2}} & {\mathbf{b}^{3}} \\{\mathbf{1}} & {\mathbf{c}^{2}} & {\mathbf{c}^{3}}\end{array}\right|\)
Answer:

Question 3.
Evaluate
\(\left|\begin{array}{ccc}{\cos \alpha \cos \beta} & {\cos \alpha \sin \beta} & {-\sin \alpha} \\{\sin \alpha \cos \beta} & {\sin \alpha \sin \beta} & {\cos \alpha}\end{array}\right|\)
Answer:
expand along c₃
-sin α (-sin α sin²β – sin α cos²β) + cosa (cosα cos² β+cosα sin²β)
= sin² α (sin² β + cos² β )+cos² α (cos² β + sin² β)
= sin²α + cos²α= 1

Question 4.
It a, b, c are real, find the factors of the determination
\(\Delta=\left|\begin{array}{lll}{\mathbf{b}+\mathbf{c}} & {\mathbf{c}+\mathbf{a}} & {\mathbf{a}+\mathbf{b}} \\{\mathbf{c}+\mathbf{a}} & {\mathbf{a}+\mathbf{b}} & {\mathbf{b}+\mathbf{c}} \\{\mathbf{a}+\mathbf{b}} & {\mathbf{b}+\mathbf{c}} & {\mathbf{c}+\mathbf{a}}\end{array}\right|\)
Answer:

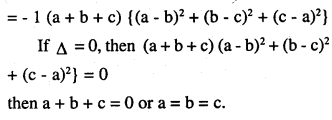
Question 5.
Solve if a ≠ 0 and
\(\left|\begin{array}{ccc}{\mathbf{x}+\mathbf{a}} & {\mathbf{x}} & {\mathbf{x}} \\{\mathbf{x}} & {\mathbf{x}+\mathbf{a}} & {\mathbf{x}} \\{\mathbf{x}} & {\mathbf{x}} & {\mathbf{x}+\mathbf{a}}\end{array}\right|=\mathbf{0}\)
Answer:

Question 6.
Prove that
\(\left|\begin{array}{ccc}{\mathbf{a}^{2}} & {\mathbf{b} \mathbf{c}} & {\mathbf{a c}+\mathbf{c}^{2}} \\{\mathbf{a}^{2}+\mathbf{a} \mathbf{b}} & {\mathbf{b}^{2}} & {\mathbf{a c}} \\{\mathbf{a b}} & {\mathbf{b}^{2}+\mathbf{b c}} & {\mathbf{c}^{2}}\end{array}\right|=4 \mathbf{a}^{2} \mathbf{b}^{2} \mathbf{c}^{2}\)
Answer:

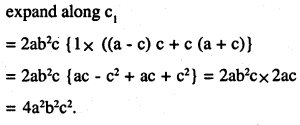
Question 7.
\(\begin{aligned}&\text { If } \mathbf{A}^{-1}=\left[\begin{array}{rrr}{3} & {-1} & {1} \\{-15} & {6} & {-5} \\{5} & {-2} & {2}\end{array}\right], \mathbf{B}=\left[\begin{array}{rrr}{1} & {2} & {-2} \\{-1} & {3} & {0} \\{0} & {-2} & {1}\end{array}\right] \text { find }\\&(\mathbf{A} \mathbf{B})^{-1}\end{aligned}\)
Answer:

Question 8.
\(\text { Let } A=\left[\begin{array}{ccc}{1} & {-2} & {1} \\{-2} & {3} & {1} \\{1} & {1} & {5}\end{array}\right], \text { verify that }\)
(i) (adj A)¹ = Adj (A¹)
(ii) (A¹)¹ = A
Answer:

Question 9.
Evaluate
\(\left[\begin{array}{ccc}{\mathbf{x}} & {\mathbf{y}} & {\mathbf{x}+\mathbf{y}} \\{\mathbf{y}} & {\mathbf{x}+\mathbf{y}} & {\mathbf{x}} \\{\mathbf{x}+\mathbf{y}} & {\mathbf{x}} & {\mathbf{y}}\end{array}\right]\)
Answer:

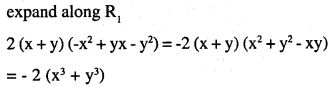
Question 10.
\(\left[\begin{array}{ccc}{\mathbf{1}} & {\mathbf{x}} & {\mathbf{y}} \\{\mathbf{1}} & {\mathbf{x}+\mathbf{y}} & {\mathbf{y}} \\{\mathbf{1}} & {\mathbf{x}} & {\mathbf{x}+\mathbf{y}}\end{array}\right]\)
Answer:

Prove the following using properties

Question 11.
\(\left[\begin{array}{lll}{\alpha} & {\alpha^{2}} & {\beta+\alpha} \\{\beta} & {\beta^{2}} & {\gamma+\alpha} \\{\gamma} & {\gamma^{2}} & {\alpha+\beta}\end{array}\right]=(\beta-\alpha)(\gamma-\alpha)(\alpha-\beta)\)
Answer:

Question 12.
\(\begin{aligned}&\left[\begin{array}{lll}{\mathbf{x}} & {\mathbf{x}^{2}} & {\mathbf{1}+\mathbf{p} \mathbf{x}^{3}} \\{\mathbf{y}} & {\mathbf{y}^{2}} & {\mathbf{1}+\mathbf{p} \mathbf{y}^{3}} \\{\mathbf{z}} & {\mathbf{z}^{2}} & {\mathbf{1}+\mathbf{p}\mathbf{z}^{3}}\end{array}\right]=(\mathbf{x}-\mathbf{y})(\mathbf{y}-\mathbf{z})(\mathbf{z}-\mathbf{x})\\&(1+p x y z)\end{aligned}\)
Answer:

Question 13.
\(\left[\begin{array}{rrr}{3 a} & {-a+b} & {-a+c} \\{-b+a} & {3 b} & {-b+c} \\{-c+a} & {-c+b} & {3 c}\end{array}\right]=3(a+b+c)(a b+b c+c a)\)
Answer:

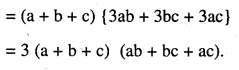
Question 14.
\(\left|\begin{array}{ccc}{1} & {1+p} & {1+p+q} \\{2} & {3+2 p} & {4+3 p+2 q} \\{3} & {6+3 p} & {10+6 p+3 q}\end{array}\right|=1\)
Answer:

Question 15.
\(\left|\begin{array}{ccc}{\sin \alpha} & {\cos \alpha} & {\cos (\alpha+\delta)} \\{\sin \beta} & {\cos \beta} & {\cos (\beta+\delta)} \\{\sin \gamma} & {\cos \gamma} & {\cos (\gamma+\delta)}\end{array}\right|=0\)
Answer:

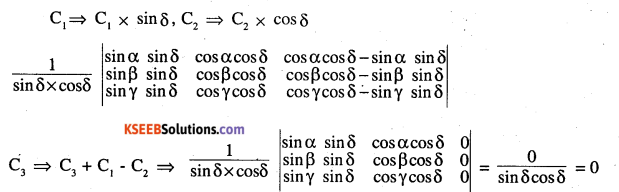
Question 16.
Solve
\(\frac{2}{x}+\frac{3}{y}+\frac{10}{z}=4\)
\(\frac{4}{x}-\frac{6}{y}+\frac{5}{z}=1\)
\(\frac{6}{x}+\frac{9}{y}-\frac{20}{z}=2\)
Answer:

Question 17.
It a, b, c are in AP, then the determinant
\(\left|\begin{array}{ccc}{x+2} & {x+3} & {x+2 a} \\{x+3} & {x+4} & {x+2 b} \\{x+4} & {x+5} & {x+2 c}\end{array}\right|\)
Answer:

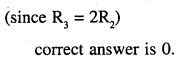
Question 18.
If x, y, z are real, then the inverse of
\(\mathbf{A}=\left|\begin{array}{lll}{\mathbf{x}} & {\mathbf{0}} & {\mathbf{0}} \\{\mathbf{0}} & {\mathbf{y}} & {\mathbf{0}} \\{\mathbf{0}} & {\mathbf{0}} & {\mathbf{z}}\end{array}\right|\)
Answer:

Question 19.
Let
\({ A }=\left[ \begin{array}{ccc} { { 1 } } & { \sin \theta } & { { 1 } } \\ { -\sin \theta } & { { 1 } } & { \sin \theta } \\ { -1 } & { -\sin \theta } & { { 1 } } \end{array} \right] { 0 }\leq \theta \leq 2\pi \)
Answer:

2nd PUC Maths Chapter 4 Determinants Miscellaneous Exercise Additional Questions and Answers

Try These Questions

Question 1.
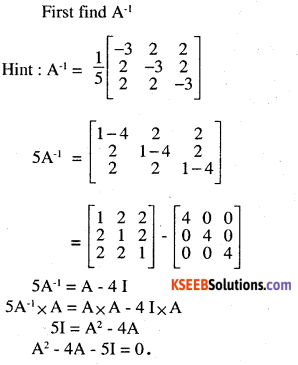
\(\text { If } \mathbf{A}=\left[\begin{array}{lll}{1} & {2} & {2} \\{2} & {1} & {2} \\{2} & {2} & {1}\end{array}\right] \text { find } A^{-1}\)
and hence prove that A² – 4A – 5 I = 0
Answer:

Question 2.
use product
\(\left[\begin{array}{ccc}{1} & {-1} & {2} \\{0} & {2} & {-3} \\{3} & {-2} & {4}\end{array}\right]\left[\begin{array}{ccc}{-2} & {0} & {1} \\{9} & {2} & {-3} \\{6} & {1} & {-2}\end{array}\right]\)
solve x – y + 2z = 1
2y – 3z = 1
3x – 2y + 4z = 2
Answer:

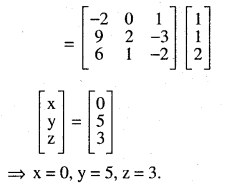
Question 3.
If the point (x, y), (a, 0), (0, b) are collinear, prove that
\(\frac{x}{a}+\frac{y}{b}=1\)
Answer:

Question 4.
\(\text { If } \Delta=\left|\begin{array}{ccc}{\mathbf{1}} & {\mathbf{1}} & {\mathbf{1}} \\{\mathbf{1}} & {\mathbf{1}+\mathbf{x}} & {\mathbf{1}} \\{\mathbf{1}} & {\mathbf{1}} & {\mathbf{1}+\mathbf{y}}\end{array}\right|, \text { then } \Delta \text { is }\)
(a) Divisible by neither x nor y
(b) Divisible by y but not x
(c) Divisible by x but not y
(d) Divisible by both x and y [AIEEE 2007]
Answer:

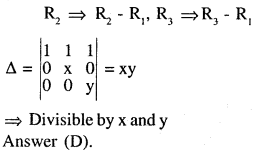
Question 5.
If a, b, c are positive and unequal, show that the value of the determinant
\(\left|\begin{array}{lll}{\mathbf{a}} & {\mathbf{b}} & {\mathbf{c}} \\{\mathbf{b}} & {\mathbf{c}} & {\mathbf{a}} \\{\mathbf{c}} & {\mathbf{a}} & {\mathbf{b}}\end{array}\right|\) is always negative [Kerala CET 09]
Answer:

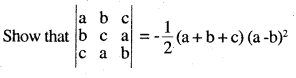
since a, b, c are positive a + b + c is positive and (a – b)² is always positive,
Δ is always negative.

Question 6.
Using properties of matrices prove that 1+abc is a factor of [CET]
\(\left|\begin{array}{lll}{\mathbf{a}} & {\mathbf{a}^{2}} &{\mathbf{1}+\mathbf{a}^{3}} \\{\mathbf{b}} & {\mathbf{b}^{2}} & {\mathbf{1}+\mathbf{b}^{3}} \\{\mathbf{c}} &{\mathbf{c}^{2}} &{\mathbf{1}+\mathbf{c}^{3}}\end{array}\right|\)
Answer:

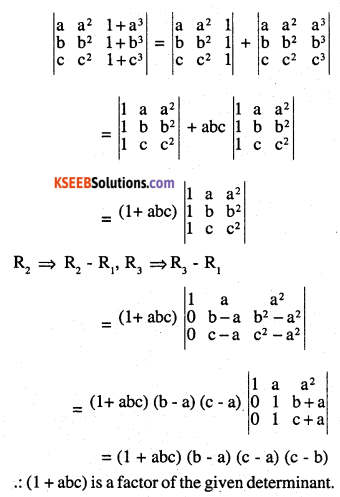
Question 7.
For what values of y is the matrix  [CBSE 2011]
\(\mathbf{A}=\left|\begin{array}{rr}{\mathbf{y}^{2}+6} & {\mathbf{2} \mathbf{y}} \\{\mathbf{y}+3} & {\mathbf{2}} \end{array}\right|\)singular.
Answer:

Question 8.
Find y
\(\left[\begin{array}{cc}{x} & {x-y} \\{2 x+y} & {7}\end{array}\right]=\left[\begin{array}{ll}{3} & {1} \\{8} & {7}\end{array}\right]\)
Answer:

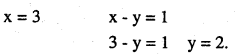
Question 9.
If A be a square matrix of order 3 x 3 then find |KA|
|KA| = kⁿ |A| when n is the order [CBSE 2007]
Answer:
|KA| = k³ |A|

Question 10.
Evaluate  [PUC 2009]
\(\left|\begin{array}{cccc}{\sin 30} & {\cos } & {30} \\{-\sin 60} & {\cos } & {60}\end{array}\right|\)
Answer:

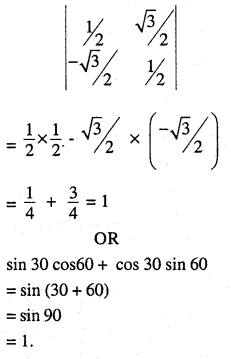
Question 11.
From the matrix equation AB = AC, we can conclude that B = C provided
(A) A is singular
(B) A is non singular
(C) A is symmetric
(D) A is skew symmetric [IIT]
Answer:
AB = AC
A^-1 (AB) = A^-1 (AC) ⇒ (A^-1 A) B = (A^-1 A) C ⇒ IB = IC ⇒ B = C
AB = AC ⇒ B = C if A¹ exist
ie,. A is non singular
correct Answer is (B)

Question 12.
A² – A + I = 0, Find the inverse if A [IIT]
Answer:
A² – A + I = 0
Pre – multiply by A^-1
A^-1 A² – A^-1 A + A^-1  I = 0
A -1 + A¹ = 0
A^-1= I – A

Question 13.
It is a triangle
\(\mathbf{A B C},\left|\begin{array}{lll}{\mathbf{1}} & {\mathbf{a}} & {\mathbf{b}} \\{\mathbf{1}} & {\mathbf{c}} & {\mathbf{a}} \\{\mathbf{1}} & {\mathbf{b}} & {\mathbf{c}}\end{array}\right|=\mathbf{0}\)
then find the value of sin²A+ sin²B+ sin²C [Karnataka CET 2002]
Answer:

Question 14.
Let A, B be two square matrices such that A + B = AB, then  [Karnataka CET]
(A) AB = BA
(B) AB = -BA
(C) AB + 2BA = 0
(D) None of these
Ans:
A + B = AB A + B – AB = 0
A + B – AB + I = 0+1
(A – I)(B – I) = 1
⇒ A -1 inverse of B -1
(B -1) (A -1) = I
BA – B – A + = I
BA – (B + A) ⇒ BA = B + A
= A + B  ∴ AB = BA
Answer (A)

Question 15.
\(\mathbf{A}(\alpha)=\left[\begin{array}{cc}{\cos \alpha} & {\sin \alpha} \\{-\sin \alpha} & {\cos \alpha}\end{array}\right]\),
then show that A(α)A(β) = A (α+β) [Kerala CET]
Answer:

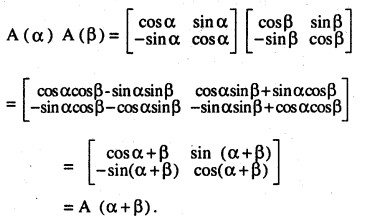
Question 16.
\(\mathbf{A}=\left[\begin{array}{ll}{\mathbf{1}} & {-\mathbf{1}} \\{\mathbf{2}} & {-\mathbf{1}}\end{array}\right], \mathbf{B}=\left[\begin{array}{ll}{\mathbf{a}} & {-\mathbf{1}} \\{\mathbf{b}} & {-\mathbf{1}}\end{array}\right] \text { and }(\mathbf{A}+\mathbf{B})^{2}\)
= A² + B² Find the values of a, b
Answer: