2nd PUC Maths Question Bank Chapter 5 Continuity and Differentiability Ex 5.1

Students can Download Maths Chapter 5 Continuity and Differentiability Ex 5.1 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Maths Question Bank Chapter 5 Continuity and Differentiability Ex 5.1

2nd PUC Maths Continuity and Differentiability NCERT Text Book Questions and Answers Ex 5.1

Question 1.
Prove that the function f (x) = 5x – 3 is Continuous at x = 0, at x = – 3 and at x = 5.
Answer:

Question 2.
Examine the continuity of the function f (x) = 2x² – 1 at x = 3.
Answer:

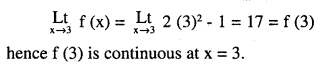
Question 3.
Examine the following functions for continuity.

(a) f (x) = x – 5
Answer:
Let ‘a’ be any real, then

it is continuous at x = a, i.e. f is continuous function as it is continuous at every point of its domain.

(b)
\((x)=\frac{1}{x-5}, x \neq 5\)
Answer:

(c)
\(f(x)=\frac{x^{2}-25}{x+5}, x \neq-5\)
Answer:
Here f(x) is a rational function and its domain D₁ = R – {-5}

(d) \(f(x)=|x-5|\)
Answer:

Question 4.
Prove that the function f (x) = xⁿ is continuous at x = a, where is a positive integer.
Answer:

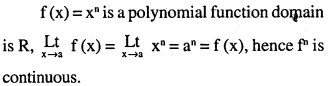
Question 5.
It is the function f defined by
\(f(x)=\left\{\begin{array}{l}{x, \text { if } x \leq 1} \\{5, \text { if }x>1}\end{array}\right.\)
continous at x = 0? At x = 1? At x = 2?
Answer:

Question 6.
Find all points of discontinuity of f, where f is defined by
\(f(x)=\left\{\begin{array}{l}{2 x+3, \text { if } x \leq 2} \\{2 x-3, \text { if } x>2}\end{array}\right.\)
Answer:

since LHL ≠ RHL
limit does not exist and is discontinuous at x = 2 The function is continuous every where
except x = 2
∴ x = 2 is the point of discontinuity.

Question 7.
\(f(x)=\left\{\begin{array}{r}{|x|+3, \text { if } x \leq-3} \\{-2 x, \text { if }-3<x<3} \\{6 x+2, \text { if } x \geq 3}\end{array}\right.\)
Answer:

since LHL ≠ RHL
limit does not exist and hence discontinuous at x = 3
However we can prove that the function is continuous at
a < -3, a > 3 and also at -3 < a <3

Question 8.
\(\mathbf{f}(\mathbf{x})=\left\{\begin{array}{l}{\frac{|\mathbf{x}|}{\mathbf{x}}, \text { if } \mathbf{x} \neq \mathbf{0}} \\{\mathbf{0}, \text { if } \mathbf{x}=\mathbf{0}}\end{array}\right.\)
Answer:


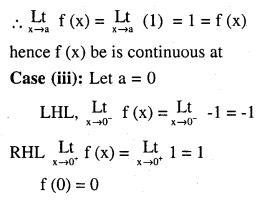
Since LHL ≠ RHL  ≠ f(0), limit does not exist
∴ It is discontinuous at x = 0.

Question 9.
\(f(x)=\left\{\begin{array}{l}{\frac{x}{|x|}, \text { if } x<0} \\{-1, \text { if } x \geq 0}\end{array}\right.\)
Answer:

Question 10.
\(f(x)=\left\{\begin{array}{l}{x+1, \text { if } x \geq 1} \\{x^{2}+1, \text { if } x<1}\end{array}\right.\)
Answer:

Question 11.
\(f(x)=\left\{\begin{array}{l}{x^{3}-3, \text { if } x \leq 2} \\{x^{2}+1, \text { if } x>1}\end{array}\right.\)
Answer:

LHL = RHL function is continuous at x = 2
∴ function is continuous every where
∴ There is no point of discontinuity

Question 12.
\(f(x)=\left\{\begin{array}{ll}{x^{10}-1,} & {\text { if } x \leq 1} \\{x^{2},} & {\text { if } x>1}\end{array}\right.\)
Answer:
The domain of the function is R

LHL ≠ RHL, function is not continuous
∴ only point of discontinuity is at x = 1

Question 13.
Is the function defined by
\(f(x)=\left\{\begin{array}{l}{x+5, \text { if } x \leq 1} \\{x-5, \text { if } x>1}\end{array}\right.\)
a continuous function ?
Answer:
The domain of the function is R
Let a ∈ R be any arbitrary point on R

since LHL ≠ RHL, function is not continuous.
Hence the point of discontinuity is x = 1.

Question 14.
Discuss the continuity of the function f, where f is defined by.
\(f(x)=\left\{\begin{array}{l}{3, \text { if } 0 \leq x \leq 1} \\{4, \text { if } 1<x<3} \\{5, \text { if } 3 \leq x \leq 10}\end{array}\right.\)
Answer:
Here domain [0,1] U [2] U [3, 10]
Case (i): Let a domain and a = 0 The function is defined only on the right of a and the function is 3 for all values right of a hence continuous at a = 0.

Case (ii): 0 < a < 1
The function take the value 3 for all a between and 1, hence continuous 0 < a < 1 Case

Case (iii): a = 1
The function is defined only on the left of and it takes the value 3 every where hence continuous when a = 1.

Case (iv): a = 2 / f (a) = f (2) = 4. But it is not defined either in the left of 2 or in the right of 2 hence it can’t be continuous at x = 2.

Case (v): a = 3
The function is defined only to the right of a and takes the value of 5 through out. Hence it is continuous.

Case (vi): 3 < a < 10
The function take the value 5 between 3 and 10 and hence continuous when 3 < a < 10.

Case (vii): a = 10
The function is defined only on the left of 10 and takes the value 5 through out. Hence the function is continuous at a = 10.
∴ 2 is the only point of discontinuity.

Question 15.
\(f(x)=\left\{\begin{array}{l}{2 x, \text { if } x<0} \\{0, \text { if } 0 \leq x \leq 1} \\{4 x, \text { if } x>1}\end{array}\right.\)
Answer:
Case (i) : The domain of the function is R

f (1) = 0, LHL ≠ RHL hence discontinuous at x = 1
How ever the function is continuous
when a < 0, 0 < a < 1 and a > 1
hence x = 1 is the only point of discontinuity.

Question 16.
\(f(x)=\left\{\begin{aligned}-2, & \text { if } x \leq-1 \\2 x, & \text { if }-1<x \leq 1 \\2, & \text { if } x>1\end{aligned}\right.\)
Answer:

LHL = RHL = f (1), fⁿ is continuous we can also prove that the function is continuous when a < -1, -1 < a < 1 and a > 1. The function is continuous at all point in R.

Question 17.
Find the relationship between a and b so that the function f defined by
\(f(x)=\left\{\begin{array}{l}{a x+1, \text { if } x \leq 3} \\{b x+3, \text { if } x>3}\end{array}\right.\)
is continuos at x = 3.
Answer:

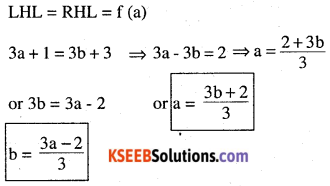
Question 18.
For what value of λ is the function defined by
\(f(x)=\left\{\begin{array}{ll}{\lambda\left(x^{2}-2 x\right),} & {\text { if } x \leq 0} \\{4 x+1,} & {\text { if } x>0}\end{array}\right.\)
continous at x = 0 ? what about continuity at x = 1?
Answer:

∴ For any value of λ, the function is discontinuous, how ever at x = 1 and x = -1.
we can prove that the function is continuous.

Question 19.
Show that the function defined by g (x) = x – [x] is discontinuous at all integral points. Here [x] denotes the greatest less than or equal to x.
Ans:
Let g (x) = h (x) – q (x)
where h (x) = x and q (x) = [x]
h (x) = x, being a polynomial function continuous every where q (x) = [x]

since LHL ≠ RHL, function is not continuous
∴ q (x) is not continuous
∴ h (x) – q (x) is not continuous
∴ g (x) is not continuous

Question 20.
Is the function defined by f (x) = x² – sin x + 5 continuous at x = π?
Answer:

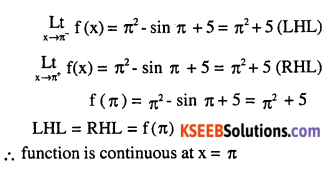
Question 21.
Discuss the continuity of the following functions:
(a) f (x) = sin x + cos x
here the domain is R
Answer:
Let a ∈ R,
\(\underset { x\longrightarrow a }{ Lt } f(x)=sin\quad x\quad =\underset { x\longrightarrow a }{ Lt } (sin\quad x\quad + cos\quad x)\)
= sin a + cos a
= f (a) = RHL = LHL
∴ function is continuous everywhere.

(b) f (x) = sin x – cos x
Answer:
Here the domain is R. Let a ∈ R
\(\underset { x\longrightarrow a }{ Lt } f(x)=sin\quad x\quad =\underset { x\longrightarrow a }{ Lt } (sin\quad x\quad – cos\quad x)\)
= sin a – cos a
= f (a) = RHL = LHL
function is continuous at x = a, a ∈ R

(c) f (x) = sin x. cos x
Answer:
Let a ∈ R where the domain is R
Lt f (_x) = Lt gin x cos x = sin a cos a = f (a)
\(\underset { x\longrightarrow a }{ Lt } f(x)=sin\quad x\quad =\underset { x\longrightarrow a }{ Lt } (sin\quad x\quad cos\quad x)\)
= sin a cos a = f(a)
hence the function is continuous at x = a, a ∈ R

Question 22.
Discuss the continuity of the cosine, cosecant, secant and cotangent functions.
Ans:
Cosine: Domain of the function is R.
Let x = a + h
\(\underset { x\longrightarrow a }{ Lt } f(x)=\underset { h\longrightarrow 0 }{ Lt } (a+h)\)


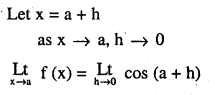
∴ function is continuous every where similarly we can prove that
Secant and cotangent are also continuous ^where ever it is defined.

Question 23.
Find all points of discontinuity of f, where
\(\mathbf{f}(\mathbf{x})=\left\{\begin{array}{l}{\frac{\sin \mathbf{x}}{\mathbf{x}}, \text { if } \mathbf{x}<\mathbf{0}} \\{\mathbf{x}+\mathbf{1}, \text { if } \mathbf{x} \geq \mathbf{0}}\end{array}\right.\)
Answer:
The domain is R, Let a ∈ R
It can be proved that the function is continuous when a < 0

Question 24.
Determine if f defined by
\(\mathbf{f}(\mathbf{x})=\left\{\begin{array}{ll}{\mathbf{x}^{2} \sin \frac{1}{\mathbf{x}},} & {\text { if } \mathbf{x} \neq 0} \\{\mathbf{0},} & {\text { if } \mathbf{x}=\mathbf{0}}\end{array}\right.\)
is a continuous functions ?
Answer:
Let a ∈ R where R is the domain of f(x)


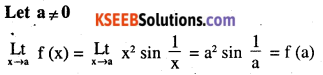
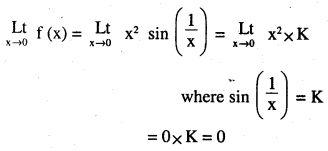
Hence the function is continous when a ≠ 0
Let a = 0 f (x) = 0
∴ function is continuous at x = 0
∴ f is continuous every where.

Question 25.
Examine the continuity of f, where f is defined by
\(f(x)=\left\{\begin{array}{ll}{\sin x-\cos x,} & {\text { if } x \neq 0} \\{-1,} & {\text { if } x=0}\end{array}\right.\)
Answer:

Find the value of k so that the function f is continuous at the indicated point in Exercises 26 to 29.

Question 26.
\(f(x)=\left\{\begin{array}{ll}{\frac{k \cos x}{\pi-2 x},} & {\text { if } x \neq \frac{\pi}{2}} \\{3,} & {\text { if } x=\frac{\pi}{2}}\end{array} \text { at } x=\frac{\pi}{2}\right.\)
Answer:

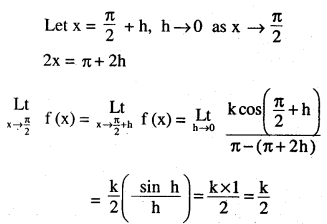
Question 27.
\(f(x)=\left\{\begin{array}{ll}{k x^{2},} & {\text { if } x \leq 2} \\{3,} & {\text { if } x>2}\end{array} \text { at } x=2\right.\)
Answer:

Question 28.
\(f(x)=\left\{\begin{array}{ll}{k x+1,} & {\text { if } x \leq \pi} \\{\cos x,} & {\text { if } x>\pi}\end{array} \text { at } x=\pi\right.\)
Answer:

Question 29.
\(f(x)=\left\{\begin{array}{ll}{k x+1,} & {\text { if } x \leq 5} \\{3 x-5,} & {\text { if } x>5}\end{array} \text { at } x=5\right.\)
Answer:

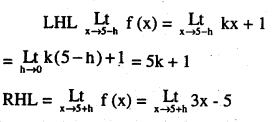
Question 30.
Find the values of a and b such that the function defined by
\(f(x)=\left\{\begin{aligned}5, & \text { if } x \leq 2 \\a x+b, & \text { if } 2<x<10 \\21, & \text { if } x \geq 10\end{aligned}\right.\)
is a continous function.
Answer:

Question 31.
Show that the function defined by f (x) = cos (x²) is a continuous function.
Answer:
Let h (x) = cos x, g (x) x², x∈ R
hog (x) = h [x²] = cos x² = f (x) .
Being polynomial function x² is continuous on R.
Being trigonometric function cos x is continuous on R in the domain.
Since h (x) is continuous and g (x) is continuous hog (x) is also continuous on R.
∴ f (x) is also continuous on R.

Question 32.
Show that the function defined by is a continuous function.
Answer:
The domain of f (x) is R
Let h (x) = cos x, g (x) = |x|
goh (x) = g (cos x) = |cos x| = f (x)
cos x and |x| are continuous on R as they are trigonometric function and modulus function. g(x) and h (x) are continuous and hence
goh (x) is also continuous, hence |cosx| is continuous on R.

Question 33.
Examine that sin |x| is a continuous function. 3
Answer:
Let g (x) = sin x and h (x) = |x|.
Both g (x) and h (x) are continuous on R
goh (x) = g |x| = sin |x| = f (x) is continuous on R.

Question 34.
Find all the points of discontinuity of f defined by f (x) = x – x +1.
Answer:
The domain is R Let g (x) = |x|, and h (x) = |x +1|
∴ g(x)-h(x)= |x| – |x + 1| =f(x)
g (x) and h (x) are continuous on R
∴ g (x) – h (x) are also continuous on R
f (x) is continuous on R.
∴ So no points of discontinuity present on R.