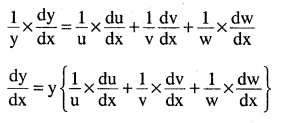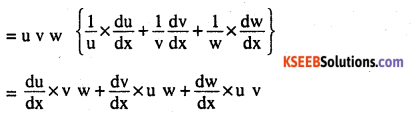Students can Download Maths Chapter 5 Continuity and Differentiability Ex 5.5 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 5 Continuity and Differentiability Ex 5.5
2nd PUC Maths Continuity and Differentiability NCERT Text Book Questions and Answers Ex 5.5
Differentiate the functions given in Exercises 1 to 11 w.r.t. x.
Question 1.
cos x. cos 2x. cos 3x
Answer:
Let y = cos x. cos 2x.cos 3x
log y = log cos x + log cos 2x + log cos 3x

![]()
Question 2.
\(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\)
Answer:
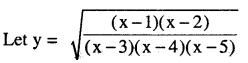
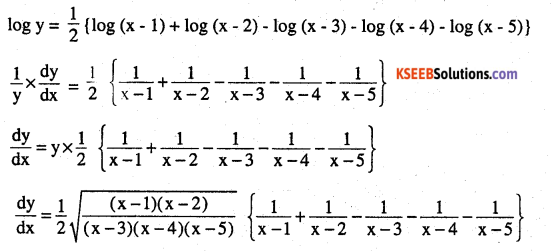
Question 3.
\((\log x)^{\cos x}\)
Answer:

![]()
Question 4.
\(x^{x}-2^{\sin x}\)
Answer:

Question 5.
\((x+3)^{2} \cdot(x+4)^{3} \cdot(x+5)^{4}\)
Answer:
Let y = (x + 3)2 (x + 4)3 (x + 5)4
log y = 2 log (x + 3) + 3 log (x + 4) + 4 log (x + 5)
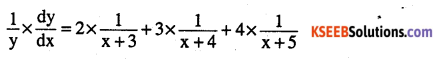
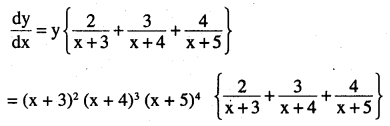
Question 6.
\(\left(x+\frac{1}{x}\right)^{x}+x^{\left(x+\frac{1}{x}\right)}\)
Answer:

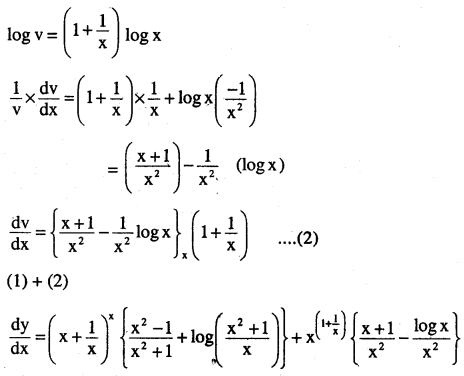
![]()
Question 7.
(log x)x + xlogx
Answer:

Question 8.
\((\sin x)^{x}+\sin ^{-1} \sqrt{x}\)
Answer:
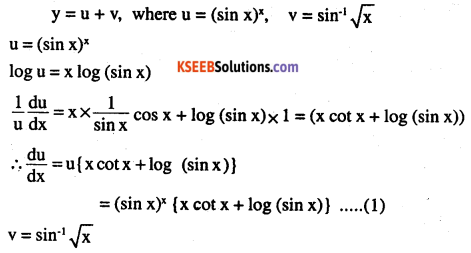
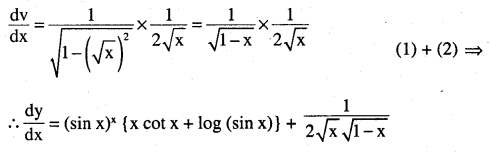
![]()
Question 9.
\(\mathbf{x}^{\sin \mathbf{x}}+(\sin \mathbf{x})^{\cos \mathbf{x}}\)
Answer:

Question 10.
\(x^{ xcos\quad x }+\frac { x^{ 2 }+1 }{ x^{ 2 }-1 } \)
Answer:
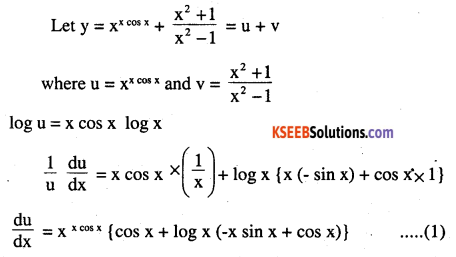
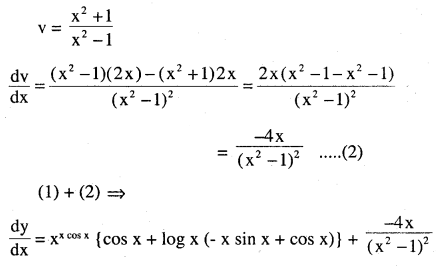
![]()
Question 11.
\((x \cos x)^{x}+(x \sin x)^{\frac{1}{x}}\)
Answer:
let y = \((x \cos x)^{x}+(x \sin x)^{\frac{1}{x}}\)
u = (x cos x )x
log u = x log (x cos x)

find \(\frac{\mathrm{d} y}{\mathrm{d} x}\)of the given in exercise 12 to 15
Question 12.
xy + yx = 1
Answer:
Let u + v = 1 where u = xy and v = yx

![]()
Question 13.
yx = xy
Answer:
Take log on both sides
x log y = y log x
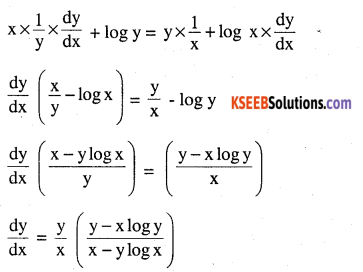
Question 14.
\(\mathbf{x y}=\mathbf{e}^{(\mathbf{x} \cdot \mathbf{y})}\)
Answer:
log xy = (x-y) log e
log(xy) = (x – y)
diff : on both sides

Question 15.
\((\cos x)^{y}=(\cos y)^{x}\)
Answer:
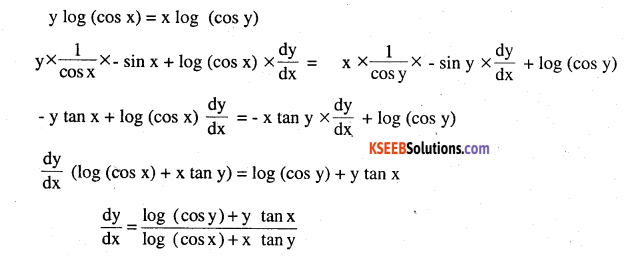
![]()
Question 16.
Find the derivative of the function given by
f (x) = (1 + x) (1 + x2) (1 + x4) (1 + x8) and hence find f'(1).
Answer:
f (x) = (1 + x) (1 + x2) (1 + x4) (1 + x8)
log f (x) = log (1 + x) + log (1 + x2) + log (1 + x4) + log (1 + x8)

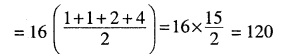
Question 17.
Differentiate (x2 – 5x + 8) (x3 + 7x + 9) in three ways mentioned below:
(i) by using product rule
(ii) by expanding the product to obtain a single polynomial
(iii) by logarithmic differentiation.
Do they all give the same answer ?
Answer:

Question 18.
If u, v, and w are function of x, then show that
\(\frac{d}{d x}(u, v, w)=\frac{d u}{d x} v \cdot w+u \cdot \frac{d v}{d x} w+u . v \frac{d w}{d x}\)
in two ways – first by repeated aplication of product rule, second by logarithmic differentiation.
Answer:
Let y = uvw (Logarithmic differentiation) log
log y = log u +log v + low w