Students can Download Maths Chapter 8 Application of Integrals Ex 8.1 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 8 Application of Integrals Ex 8.1
2nd PUC Maths Application of Integrals NCERT Text Book Questions and Answers Ex 8.1
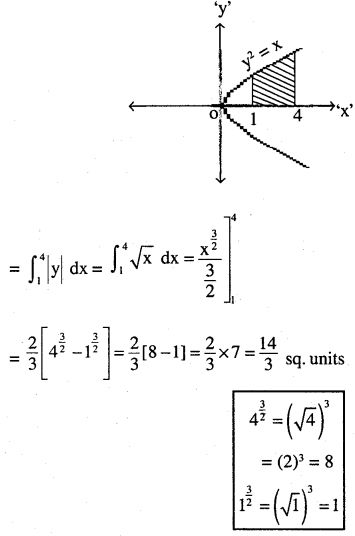
Question 1.
Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Answer:
We know that y2 = x represents right hand parabola with vertex (0,0)
Required area is shaded area:-
If not mentioned above/below/any quadrant, so we should take above and below
\(\Rightarrow 2 \times \frac{14}{3}=\frac{28}{3} \text { sq. units. }\)
![]()
Question 2.
Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Answer:
We know y2 = 9x is right handed parabola with vertex (0,0)
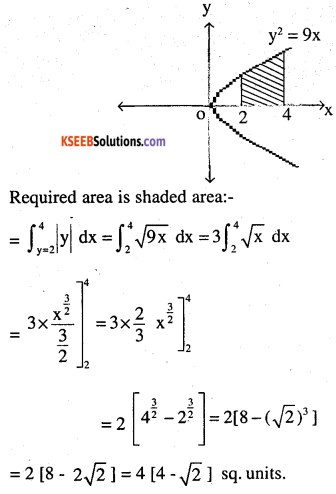
Question 3.
Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y – axis in the first quadrant.
Answer:
We know x2 = 4y is upward parabola with vertex (0,0).
Required area is shaded area:-
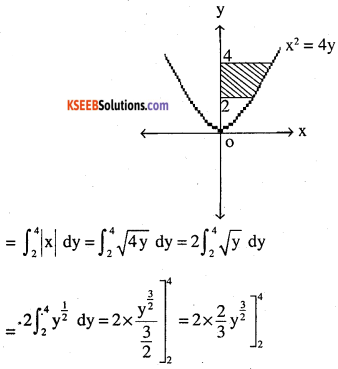
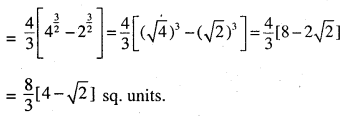
Question 4.
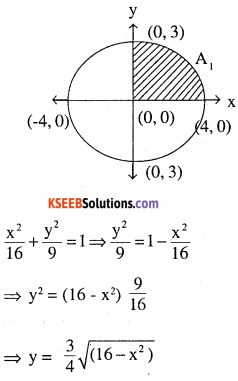
Find the area of the region bounded by the ellipse
\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)
Answer:
We know curve is ellipse vertex (0,0) major axis is ‘x’ and major ‘y’
Area of given area is = 4 x (Area of shaded)
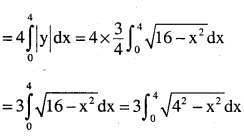

![]()
Question 5.
Find the area of the region bounded by the ellipse
\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\)
Answer:
We know curve is ellipse vertex (0,0) major axis is ‘y’ and major ‘x’
Area of given area is = 4 x (Area of shaded)
\(=4 \times \int_{0}^{2}|y| d x\)
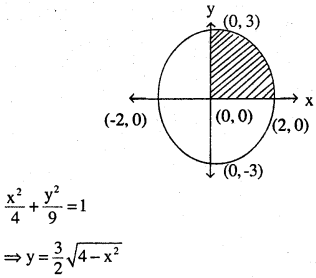

Question 6.
Find the area of the region in the first quadrant enclosed by x-axis, line \(x=\sqrt{3}\) y and the circle x2 + y2 = 4.
Answer:

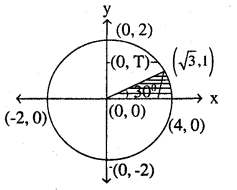

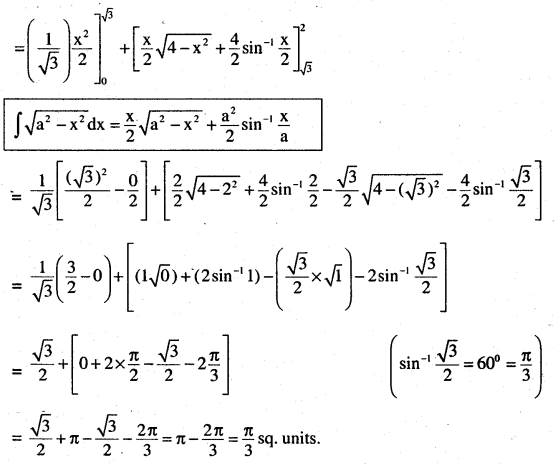
![]()
Question 7.
Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line \(x=\frac{a}{\sqrt{2}} \)
Answer:
Circle x2 + y2 = a2 is circle with centre (0,0) and radius
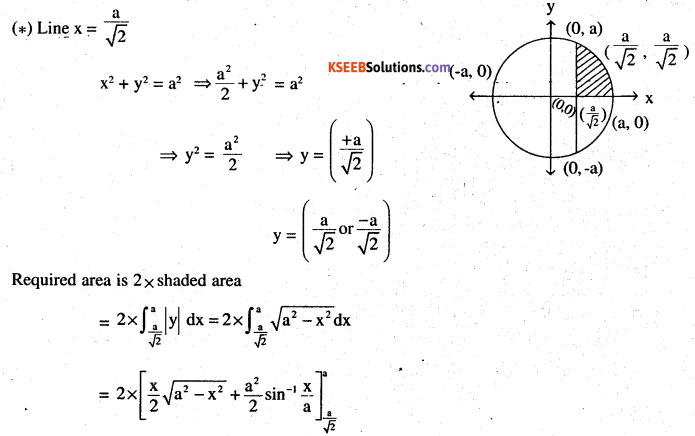

Question 8.
The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Answer:
(1) x = y2 is right hand parabola with vertex (0, 0) ⇒ y2 = x
As area between y2 = x, x = 4 is divided into 2 parts by x = a,
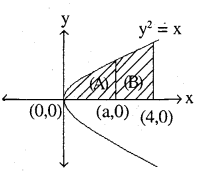
so,(area under y2 = x, x = 0 to x = a) =(area under y2 = x, x = a, x = 4)
⇒area (A) = area (B)

![]()
Question 9.
Find the area of the region bounded by the parabola y = x2 and y = |x|
Answer:
(1) As we know x2 = y is a upward parabola with vertex (0,0)
(2) line ⇒ y = |x|
So if y = 1,x = 1 (1,1)
y = -1,x = 1 (-1, 1)
y = 2, x = 2 (2, 2)
y = 2, x = 2 (-2,2)
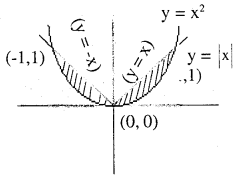
Area required is the shaded area
= 2 x (area of one half (lets take it of 1st quadrant))
= 2 x [(area under line y = |x|) – area under parabola y = x]

Question 10.
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2.
Answer:
(1) Curve x2 = 4y is upward parabola vertex (0, 0)
(2) Line x = 4y – 2 (put 4y = x2 in it)
⇒ x = x2 – 2 ⇒ x2– x – 2 = 0
⇒ x = 2, -1
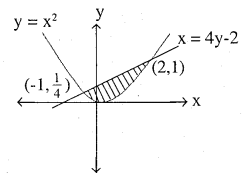
So when x = 2 , y = 1 (2,1)
\(x=-1, \quad y=\frac{1}{4} \quad\left(-1, \frac{1}{4}\right)\)
So, Area required is shaded area:-
= [Area under line x = 4y – 2 from (-1 to 2) (x axis) – [Area under x2 = 4y from
-1 to 2 (x axis)]
\(\int_{-1}^{2}\left(\frac{x+2}{4}\right) d x-\int_{-1}^{2} \cfrac{x^{2}}{4} d x\)
As solving along ‘x’ axis ,so we take values in terms of x to solve
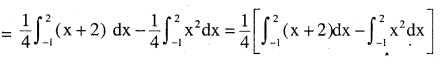

![]()
Question 11.
Find the area of the region bounded by the curve y2 = 4x and the line x = 3.
Answer:
(1) Curve y2 = 4x is right handed parabola with vertex (0,0) y
(2) Line x = 3, so points are (3,0) (3, 1) (3, 2)
\(\Rightarrow y^{2}=12 \Rightarrow y=\pm 2 \sqrt{3}\)
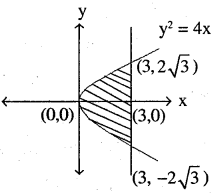
(3) But as we solve with respect to ‘x’ axis, so need only ‘x’ values:-
⇒Required area is shaded area = 2 X area of upper half of shaded region

Choose the correct answer in the following Exercise 12 and 13
Question 12.
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is
(A) π
(B)\(\frac{\pi}{2}\)
(C)\(\frac{\pi}{3}\)
(D)\(\frac{\pi}{4}\)
Answer:
(1) Circle is x2 + y2 = 4 with centre (0, 0) and radius 2.
se required area is shaded area of circle from
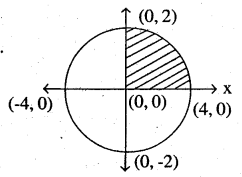

so answer is (A) π unit ……
OR
As circle of radius 2. so area of circle = πr2
π x 22 = 4π
As we need area of only 1 quadrant
\(\Rightarrow \frac{1}{4} \times \text { area of circle }=\frac{1}{4} \times 4 \pi=\pi \mathrm{sq.} \text { units. }\)
option (A)
![]()
Question 13.
Area of the region bounded by the curve y2 = 4x, y – axis and the line y = 3 is
(A) 2
(B) \(\frac{9}{4}\)
(C) \(\frac{9}{3}\)
(D) \(\frac{9}{2}\)
Answer:
(1) Curve y2 = 4x is right handed parabola
(2) line y = 3 ⇒ points in line are (0,3), (1,3), (2,3),(3, 3), (-1,3) (-2, 3) etc
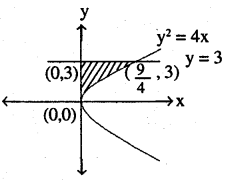
(3) Pt where line meets y2 = 4x is solved by . solving the equation
as we know y = 3 \(\text { so } x=\frac{3^{2}}{4} \Rightarrow \frac{9}{4}\)
\(\text { so pt is }\left(\frac{9}{4}, 3\right)\)
(If we solve along ‘y’ axis)
[Here to solve along ‘x’ axis, it is tough as to get equation of line in terms of ‘x’ is tough.
(4) So area is area under parabola from y = 0 to y = 3.
