Students can Download 2nd PUC Physics Previous Year Question Paper June 2019, Karnataka 2nd PUC physics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Physics Previous Year Question Paper June 2019
Time: 3 Hrs 15 Min
Max. Marks: 70
Introductions:
- All parts are compulsory.
- Answer without relevant diagram/figure/circuit wherever necessary will not carry any marks.
- Numerical problems solved without writing the relevant formulae carry no marks.
Part – A
I. Answer the following questions in one sentence each: ( 10 × 1 = 10 )
Question 1.
How does the Resistance of a Conductor Vary with its length?
Answer:
Directly proportional OR As length increases, resistance increases.
Question 2.
State Ampere’s circuital law.
Answer:
The line integral of magnetic field around a closed path in vacuum is equal to p o times the total current passing the closed path.
Question 3.
When does the force acting on a charged particle moving in a uniform magnetic field is Maximum?
Answer:
Charged particle moves perpendicular to field OR θ = 90° where θ is the angle between direction of magnetic field and velocity.
Question 4.
Define declination?
Answer:
The angle between the geographic meridian and magnetic meridian at that place.
Question 5.
What is Retentivity?
Answer:
The property of magnetic material to retain magnetism even in the absence of magnetizing field.
Question 6.
Write any one advantage of Eddy Current.
Answer:
- Induction furnace
- Magnetic braking in trains
![]()
Question 7.
What is the rest mass of photon?
Answer:
Zero
Question 8.
Name the Spectral Series of Hydrogen atom which lies in the Visible region of electro magnetic spectrum.
Answer:
Balmer series.
Question 9.
What are isotopes?
Answer:
The nuclei which have the same atomic number but different mass numbers.
Question 10.
Mention one need for modulation.
Answer:
- To reduce the size of the antenna
- Effective power radiated by the antenna
- Mixing up of signals from different transmitters
Part -B
II. Answer any five of the following questions: ( 5 × 2 = 10 )
Question 11.
Write any two limitations of Ohm’s law.
Answer:
- It is not applicable for metallic conductor at very low and very high temperatures.
- It is not applicable for semiconductors, super conductors, triodes.
Question 12.
Draw a neat labelled diagram of Cyclotron.
Answer:
Cyclotron is a device to accelerate charged particles or ions to high energies. Cyclotron uses both electric field and magnetic field to increase the energy of charged particles.
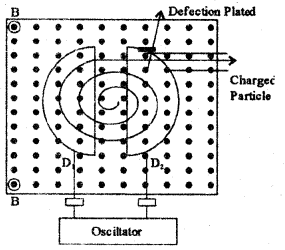
Question 13.
Mention an expression for the magnetic field produced at the center on the axis of a current carrying Solenoid and explain the terms.
Answer:
B = μonI
Where μo = Permeability of free space
n = number of turns per unit length of solenoid
I = current through solenoid.
Question 14.
State and Explain Gauss’s Law in magnetism.
Answer:
The net magnetic flux through any closed surface is alwsays zero
Σ\(\overrightarrow{\mathrm{B}}\overrightarrow{\Delta \mathrm{S}}\) = 0
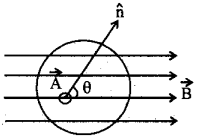
consider a closed surface S in a uniform
M.F. \(\overrightarrow{\mathrm{B}}\)Let \(\overrightarrow{\Delta \mathrm{S}}\) be a small area element of this surface with along its normal

Question 15.
What is a Transformer? Mention any one sources of Energy loss.
Answer:
A transformer is a device used to change AC voltage by using the principle of mutual induction.
- Loss due to flux leakage
- Loss due to eddy current
![]()
Question 16.
Write any two uses of ultra violet rays.
Answer:
- Used in LASIK eye surgery
- UV lamps are used to kill germs in water purifiers
- Disinfection for virus and bacteria.
- To produce photo electric current in Burglar alarm.
Question 17.
Give the two differences betwene Collector region and Emitter region of a transistor.
Answer:
Collector Region
- Moderately doped
- Large in size
- Collects charge carriers
Emitter region
- Heavily doped
- Moderate in size
- Emits charge carriers.
Question 18.
Draw a Block diagram showing the important components in a Generalized Communication System.
Answer:
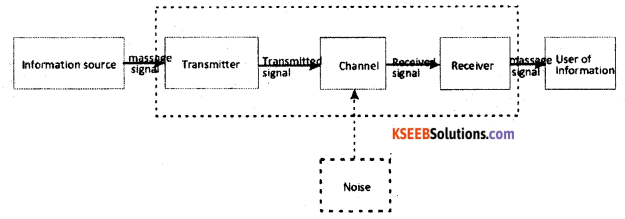
Part-C
III. Answer any Jive of the following questions. ( 5 × 3 = 15 )
Question 19.
Mention any three properties of
Electric field lines.
- Field lines are continuous curves without any breaks
- Two field lines cannot cross each other
- Electrostatic field lines start at positive charges and end at negative charges
- They do not form closed loops.
Question 20.
Obtain an expression for effective capacitance of two capacitors connected in series. (July -2018, Q.No.20)
Answer:
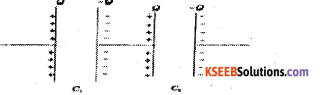
Let C1, C2 -capacitance of 2 capacitors connected in series
Q-charge on each capacitor
V1 V2 – pd across C1 and C2
V-Total voltage drop across the combination
Then V = V1 + V2 (1) ;
Also Q = CV
V1 = \(\frac{\mathrm{Q}}{\mathrm{C}_{1}}\) and V2 = \(\frac{\mathrm{Q}}{\mathrm{C}_{2}}\)
If system of capacitors is replaced by a single capacitor of

Question 21.
Explain with a circuit diagram how a galvanometer can be converted into an ammeter. (March – 2015, Q.No.20)
Answer:
A galvonometer can be converted into an ammeter by connecting a low resistance in parallel with it.
Let S be the low resistance connected in parallel with the galvonometer, G be the resistance parallel with the galvonometer, G be the resistance of the Galvonometer, I be the maximum current to be measured end Is be the current required, for full scale deflection in the galvonometer
Here Galvonometer and shunt resistances are connected in parallel.
∴ potential difference across ‘s’ = potential difference across G
(I – Ig)s = IgG
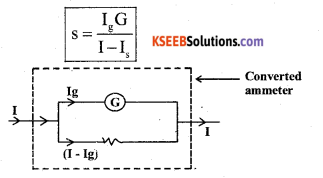
Question 22.
Write any three distinguishing properties between diamagnetic and ferromagnetic materials.
Answer:
Refer March – 2019, Q.No. 20

One ampere is that steady current through each of infinitely long straight parallel conductors of negligible area of cross section separated by a distance of lm in vacuum, then each experience a force of 2 × 10-7 Nm-1.
Question 23.
Derive the relation between focal length and radius of curvature of a concave mirror.
Answer:
Consider a ray parallel to principal axis of a concave mirror of small aperture incident at M. The ray reflected along MF as shown. Let θ is the angle of incidences. As the aperture is small, angle θ is small and are PM is considered as straight segment.
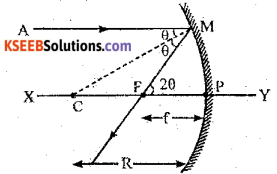
From the Δle MCP
tan θ = \(\frac{P M}{P C}\)
tan θ = \(\frac{P M}{R}\)
since θ is small tan = θ
∴ θ = \(\frac{P M}{R}\) ……. 1
From the Δle PFM
tan 2θ = \(\frac{P M}{P F}\)
tan 2θ = \(\frac{P M}{F}\)
since θ is small tan 2θ = 2θ
∴2θ = \(\frac{P M}{F}\)
θ = \(\frac{P M}{2F}\) ……..2
From 1 and 2 \(\frac{P M}{F}\) =\(\frac{P M}{2F}\)
R = 2f
f = \(\frac{R}{2}\)
![]()
Question 24.
Using Huygens principle, show that the angle of incidence is equal to angle of reflection during a plane wavefront reflected by a plane surface.
Answer:
Departmental Model Question Paper – 2, Q.No. 24.
Law of reflection of light: Angle of incidence = angle of reflection i = r
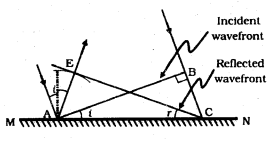
In above figure, MN in reflecting surface AB in the incident wave front FC in the reflected wave front. i in the angle of incidence. r in the angle of reflection.
Let ‘v’ be the speed of the light wave in the medium and ‘t’ be the time taken by the secondary wave letes to move from the point B to C Then the distance. BC = vt
In order to contruct the reflected wave front, Let us draw a sphere of radium AE vt, CE repersents the tangent drawn from the point e to this sphere, This tangent represents the position of the new reflected wave front.
From the figure it is observed that AE = BC vt. the triangles EAC and BAC are congruent
∴ i = r. This is the Law of reflection.
Question 25.
Name the three types of electron Emission.
Answer:
Depending upon the sources of external energy, electron emission is classified into four groups.
- Thermionic emission
- Photoelectric emission
- Field emission
- Secondary emission
Question 26.
What is NAND gate? Write its logic Symbol and Truth Table. (March – 2016 Q.No. 16)
Answer:
Symbol
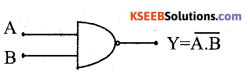
Where A & B are inputs and y is output.
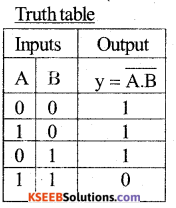
Part- D
IV. Answer any two of the following questions: ( 2 × 5 = 10 )
Question 27.
Obtain an expression for the Electric Field on the equatorial line of an Electric dipole.
Answer:
Refer Departmental Model Question Paper – 1, Q.No. 27. (March – 2017, Q.No. 27.)
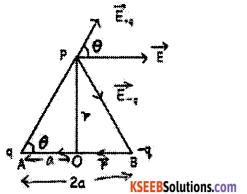
Let a point P be at a distance r from the centre of the dipole (O) Dipole length AB = 2a,
Using Pythagoras theorem, the distance of the point P from the charges is,
AP = BP = d = \(\sqrt{r^{2}+a^{2}}\)
Using, the expression for electric field due to a charge q at a distance d from it, \(\mathrm{E}=\frac{1}{4 \pi \varepsilon_{0}}\) \(\frac{\mathrm{q}}{\mathrm{d}^{2}}\) , The magnitude of the electric field at P due to the charge + q is E+q = \(\frac{1}{4 \pi \varepsilon_{0}}\) \(\frac{q}{r^{2}+a^{2}}\) The magnitude of the electric field at P due to the charge ‘-q’ is E -q = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}}{\mathrm{r}^{2}+\mathrm{a}^{2}}\)
The total field at P, \(\overrightarrow{\mathrm{E}}_{+q}\) and \(\overrightarrow{\mathrm{E}}_{-\mathrm{q}}\) are resolved in to components parallel to \(\overrightarrow{\mathrm{p}}\) and perpendicular to \(\overrightarrow{\mathrm{p}}\). The direction of p (or p) is from – q to +q.
The components normal to the dipole axis (E+qsinθ) and (E-qsinθ) cancel out as they are equal in magnitude and opposite in direction.
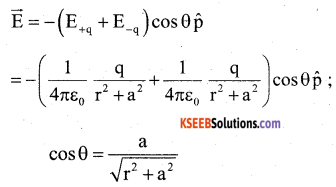
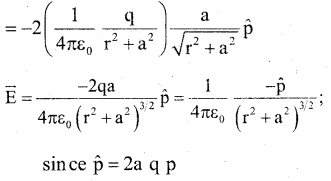
![]()
Question 28.
Derive an Expression for the Balancing ‘ condition of wheat stone Bridge.
Answer:
It is the combination of four resistances P, Q, R and S in the form of quadrilateral ABCD. A galvanometer is connected between junctions B and D. The line BD is called galvanometer arm. A battery is connected between junctions A and C. This Ac is called the battery arm.
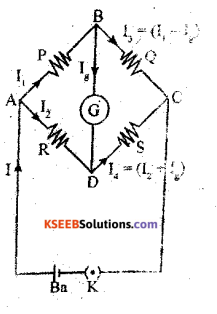
On applying Kirchhoff’s loop rule to the loop ABDA, we get
I1P – IgG – I2R = o
But for balance of network Ig = 0
I1P – I2R = o
I1P = I2R………………….. (1)
On applying Kirchhoff’s loop rule to the loop BCDB, we get
(I1 – Ig)Q – (I2 + Ig)S – Ig G = 0
I1Q – IgQ – I2 S – IgS – IgG = 0
For balance of network Ig = 0
I1Q – I2S = 0
I1Q = I2S …………..(2)
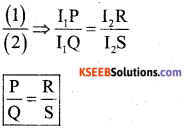
This is the condition for balance Wheatstone bridge.
Question 29.
Derive an expression for instantaneous induced emf in an A.C. generator.
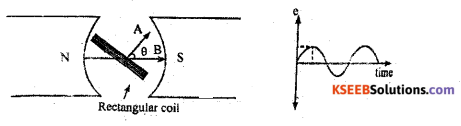
Answer:
In the above figure
N and S are poles of a magnet, θ is the angle between the directions of magnetic field B and area vector A.
When the coil is rotated in the magnetic field, the flux linked with the coil varies. At any’ instant of time ‘t’, A cosθ is the component of area vector along the direction B.
The magnetic flux linked with the coil at any instant of time ‘t’ is given by
ΦB = B x component of area vector along the field direction.
For 1 turn ΦB = BA cos θ
For n turns ΦB = nAB cos θ
ΦB = nABcosωt….(1)[∵ θ = ωt]
Where ‘ ω ’ is the angular velocity of the coil at time t.
From the Faraday’s second law,
e = [Latex]-\frac{\mathrm{d} \phi}{\mathrm{d} \mathrm{t}}[/Latex]
e = -[Latex]\frac{\mathrm{d}}{\mathrm{dt}}[/Latex][nAB cos cot] [From(l)Φ=nABcosωt]
e = (-n AB) [-sin ω t) × ω
e = nABωsinωt
e = e0 sin( ω t)
where e0 is the peak value of emf = nAB ω
V. Answer any two of the following questions: ( 2 × 5 = 10 )
Question 30.
Derive an expression for the fringe witdth of interference fringes in a double slit experiment. (March – 2014, Q.No. 30)
Answer:
Let A and B be two slits separated by a distance ‘d’. Let ‘λ’ be the wavelength of light. Let ‘D’ be the distance between the screen and the double slit.
Let ‘C’ be a point on BP such that AP « CP Path difference between the two waves reaching ‘P’ is given by BP – AP = BC =????
From the Δ BFP, BP2 = BF2 + FP2 and from the A AEP, AP2 = AE2 + EP2
BP2 – AP2 = (D2 + FP2) – (D2 – EP2)
i.e, (BP – AP) (BP – AP) = 2 (2 × \(\frac{\mathrm{d}}{2}\) )
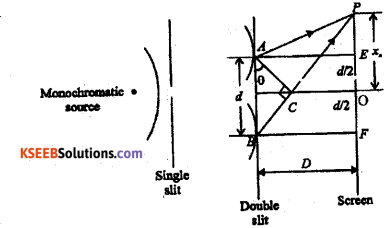
For a point ‘P’ close to ‘O’
BP ≈ AP = D
(BP – AP) (2D) = 2x.d
But (BP – AP) = BC = δ
i,e. = \(\frac{\mathrm{xd}}{D}\) or x = \(\frac{\delta \mathrm{d}}{\mathrm{D}}\)
For a constructive interference = nλ
Distance of nth bright fringe from the central bright fringe xn = n \(\frac{\lambda \mathbf{D}}{\mathrm{d}}\)
Distance of (n + l)th bright fringe from the central bright fringe xn+1 = (n + 1) \(\frac{\lambda \mathbf{D}}{\mathrm{d}}\)
By definition, Fringe width is the distance between two consecutive bright or dark fringes.
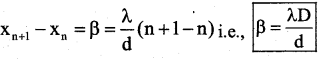
Fringe width \(\frac{\lambda}{\mathrm{d}}\) β ∝ D, β ∝ λ and β ∝ \(\frac{1}{d}\)
We can show that the fringe width between
any two dark frings is also β = \(\frac{\lambda \mathrm{D}}{\mathrm{d}}\)
Question 31.
Derive an expression for the energy of an electron in nth” stationary orbit of hydrogen atom by assuming the expression for radius. (June – 2017, Q.No. 31)
Answer:
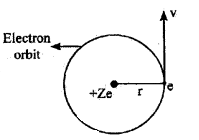
Consider an electron of mass m Electron and charge e othit revolving round the nucleus of an atom of atomic number Z in the stationary orbit of radius ‘r’. Let y be the velocity of the nucleus it also possess kinetic energy by virtue of its motion.
For stationary orbit, total energy E = KE + PE …………1
From Rutherford’s atom model,
For stationary orbit, centripetal force = Electrostatic force.
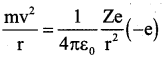
( ∵ Electrostatic force, according to Coulomb’s law)
on dividing by 2 on both sides, we get
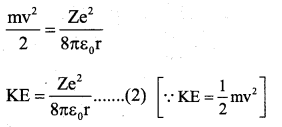
We have PE = Electric potential at a distance are due to + Ze × (-e)
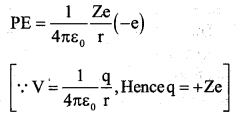
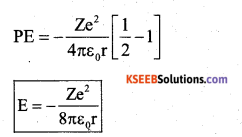
The radius 0fth permitted orbit of electron is given by
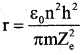
Substituting the value of ‘r’ in equation (4)
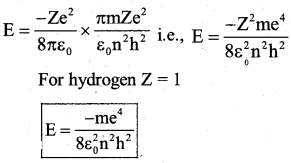
![]()
Question 32.
What is Rectification? Describe with a circuit diagram the working of a p-n junction diode as half wave rectifier with input and output waveforms.
Answer:
The process of converting ac into dc is called rectification.
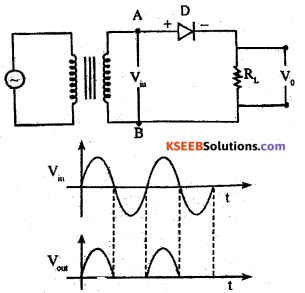
The diode D in series with a load resistor RL is connected to the secondary of the transformer. The ac voltage to be rectified is applied to the primary of the transformer. The secondary of a transformer supplies the desired ac voltage across terminals A and B. The output dc voltage is taken across the load RL.
Working: During the positive half cycle of input ac voltage, the end A becomes positive with respect to the end B. As a resùÍt the diode becomes forward biased and conducts the current. the current flows in the direction ADRLBA.
During the negative half cycle of input ac voltage, the end A becomes negative with respect to the end B. As a result the diode becomes reverse biased and does not conducts the current.
Thus the current flows through the diode during positive half cycle only. The current flows through the load RL always in the same direction. Hence dc output is obtained.
VI. Answer any three of the following questions : (3 × 5 = 15)
Question 33.
ABCD is a square of side lm. Charges of +3nC, -5nC and +3nC are placed at the comers A, B and C respectively. Calculate the work done in transferring a charge of 12µc from D to the point of intersection of the diagonals?
Solution:
Diagonal = BD = AC = 1.414m Half of diagonal = AO = BO = CO = 0.707m
Elecric potential due system of charges

Work done to transfer 12 µ C charge from D to 0
W = q[VD – V0] = 12 × 10-6[22.176 – 12.7298]
W= 1.1335 × 10-4 J
Question 34.
A network of Resistors is connected to a 16 V battery with internal resistance 1 Ω as shown in Figure below.
a) Compute the equivalent resistance of the network
b) Calculate the total current in the circuit
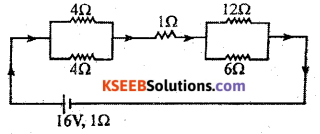
Solution:
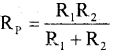
4 ohm and 4 ohm in parallel:
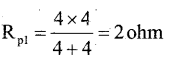
12 ohm and 6 ohm in parallel:
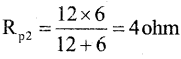
Rpl, 1 ohm and Rp2 in series : Equivalent resistance o fhetwork
Req = Rp1 + 1 + Rp2 = 2 + l+ 4 = 7 ohm
Total current in the circuit:
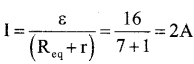
Question 35.
A sinusoidal voltage of peak value 283 V and frequency 50 Hz is applied to a series LCR circuit in which R = 3 Ω, L = 25.48 mH and C = 796 μF. Find
a) Impedance of the circuit.
b) The phase difference between the Voltage across the source and the current.
Solution:
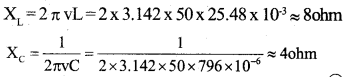

Question 36.
An object of 3cm is placed 14cm in front of a concave lens of focal length 21 cm. Find the position, Nature and size of the Image formed.
Answer:
h0 = 3cm, u = -14cm, f = -21 cm
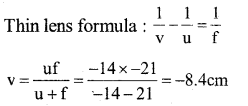
Position of image; 8.4cm from lens on same side as object
Nature of image : Virtual and erect
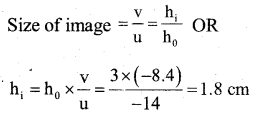
Image is dimished.
![]()
Question 37.
Calculate the binding Energy of an alpha (α) particle in Mev from the following data.
Mass of Helium Nucleus = 4.00260 u
Mass of neutron = 1.008662 u
Mass of proton = 1.007825 u.
Answer:
Alpha particle : \(_{2}^{4} \mathrm{He}\) Z = 2 and A = 4
Mass defect : Δm = [Zmp + (A-Z)mn] – M
Δm = 2 × 1.007825 + 2 × 1.008662 – 4.00260
Δ m = 2.01565 + 2.017324 – 4.00260 Δ m= 0.030374 u
Binding energy : Eb = Δm × 931 MeV = 0.030374 × 931 MeV
Eb = 28.2782 MeV