Students can Download 2nd PUC Statistics Model Question Paper 1 with Answers, Karnataka 2nd PUC Statistics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Statistics Model Question Paper 1 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 100
Note:
- Graph sheets and statistical tables will be supplied on request.
- Scientific calculators may be used.
- All working steps should be clearly shown.
Section – A
I. Answer any TEN of the following questions. (10 x 1 = 10)
Question 1.
What are vital events?
Answer:
Vital events are the events of human life such as births, deaths, marriage, divorce, sickness, adoption, migration, etc.
Question 2.
Define price relative.
Answer:
Price relative is the price in the current year expressed as the percentage of the price in the base year.
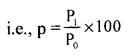
Question 3.
Write the formula for Marshall-Edgeworth’s quantity Index number.
Answer:
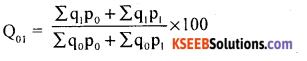
Question 4.
Define ‘time series’.
Answer:
A chronological arrangement of statistical data is called time series.
Question 5.
Write the relation between mean and variance of a Binomial distribution.
Answer:
In Binomial distribution : Mean > variance.
![]()
Question 6.
Write the p.d.f. of a normal variable with mean = 5 and variance = 9.
Answer:
Given Mean : µ = 5, and variance = σ2 = 9 i.e., σ = 3
The p.d.f. of normal variable is

Question 7.
What is type II error?
Answer:
Type II error is taking a wrong decision to accept the null hypothesis when it is actually not true.
Question 8.
Give the standard error of difference of proportions in testing the equality of proportions for large samples.
Answer:
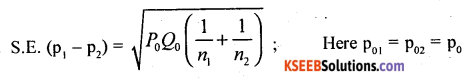
Question 9.
Define sampling distribution in statistical inference.
Answer:
The distribution of values of statistic for different samples of the same size, is called sampling distribution of statistic.
Question 10.
What do you mean by replacement problem?
Answer:
It is the problem of deciding the age at which the old equipment (Machine and their spare parts, trucks, tyres etc.,) are replaced.
![]()
Question 11.
What is pure strategy in a game?
Answer:
Pure strategy of a player is his predetermined decision to adopt a specified course of action irrespetive of the course of action of the opponent.
Question 12.
What is process control?
Answer:
Controlling the quality of the goods, during the manufacturing process itself is called process control.
Section -B
II. Answer any TEN of the following questions. (10 x 2 = 20)
Question 13.
The female population of child bearing age group in a region is 160000. The number of live births in the year in the region is recorded as 2480. Find GF.R.
Answer:

Question 14.
Mention any two uses of Index Numbers.
Answer:
- Index numbers are useful to governments in formulation of decisions and policies regarding taxation, Import – Exports, grant of licenses to new firms.
- In evaluation of purchasing power of money.
Question 15.
Mention two methods of construction of consumer price index number.
Answer:
- Aggregate Expenditure Method (A.E.M).
- Family budget method (E.B.M.).
Question 16.
Write the Normal equations for fitting the parabolic trend, y = a + bx + cx2.
Answer:
Normal equations are :
na + bΣx + cΣx2 = Σy.
aΣx + bΣx2 + cΣx3 = Σxy
aΣx2 + bΣx3 + cΣx4 = Σx2y
Question 17.
Define interpalation and extrepolation.
Answer:
Interpolation is the technique of estimating the value of dependent variable (y) for any intermediate value of the independent variable (x). Extrapolation is the technique of estimating the value of dependent variable (y) for any value of the independent variable (X) which is outside the rouge of the given series.
Question 18.
State the conditions under which Binomial distribution tends to Normal distrbution.
Answer:
Binomial distribution tends to Normal distribution when
(a) n is large (n → ∞ )
(b) Neither p nor q are very small and (3) np = µ = mean.
Question 19.
In a Normal distribution. If S.D = 12, then find Q.D and M.D.
Answer:
In Normal distribution
S.D = σ = 12
Q.D = \(\frac{2}{3}\)σ = \(\frac{2}{3}\) x 12 = 8
M.D = \(\frac{2}{3}\)σ = \(\frac{2}{3}\) x 12 = 9.6
Question 20.
Define Null and Alternative hypothesis.
Answer:
Null hypothesis is a hyopthesis which is being tested for possible rejection under the assumption that it is true, denoted by H0.
Alternative hypothesis is a hypothesis which is being accepted when the null hypothesis is rejected denoted by H1.
![]()
Question 21.
Mention two applications of chi-square distribution.
Answer:
- To test whether the population has given variance.
- To test the goodness of fit of the theoretical frequencies to the observed data.
Question 22.
What are multiple and unbounded solution in an L.P.P?
Answer:
If an L.P.P. has many optimal solutions, it is said to have multiple solution:
For some L. P.P. may not have optimal solution or the optimal value of z may be infinity, then in such cases the L.P.P. is said to have unbounded solution.
Question 23.
What is meant by stock replenishment and shortage cost in an Inventory?
Answer:
Stock replenishment is the rate at which the items are added to the Inventory to maintain a certain level.
The cost associated with delay or inability to meet the demand because of shortage of stock is called shortage cost, denoted by C2.
Question 24.
For 10 samples of 5 items each, sum of sample means = 256.8 and ΣR = 7.85. Compute 3 sigma control limits for mean chart (for n = 5, A2 = 0.58).
Answer:
Given k = 10 ΣX̄ = 256.8 , Σ R = 7.85 , n = 5
Here standards are not given,
5 im
control limits for X̄ = charts are ,
C.L = X̄ = 25.68
L.C.L = X̄ – A2R̄= 25.68 = 0.58 x 0.785 = 25.22
U.C.L = X̄ + A2R̄ = 25.68 – 0.58 x 0.785 = 26.14
Section – C
III. Answer any EIGHT- questions. (8 x 5 = 40)
Question 25.
Describe the components of a life table.
Answer:
Following are the components of a life table.
(a) lx be the number of persons living at age x.
(b) dx be the number of persons die.
(c) qx – mortality ratio, it is the probability that a person of age ‘x’ die between age x and x + 1
i.e, qx = \(\frac{\mathrm{d} \mathrm{x}}{\mathrm{l} \mathrm{x}}\)
(d) px – survival ratio, it is the probability that a person of age ‘x’ survives upto age ‘x+1′ i.e.,px = 1 – qx
(e) Lx – Total number of years lived in the aggregate by the cohort in between age x and x + 1.
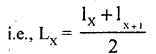
(f) Tx – Total number of years lived by the cohort after attaining the age x.
i.e., TX = LX + LX+1 + LX+2 + …..
(g) eX – It is the expectation of life at age x
i.e, \(\mathrm{e}_{\mathrm{x}}=\frac{\mathrm{T}_{\mathrm{x}}}{1_{\mathrm{x}}}\) , it is the average number of years a person aged x can expected to live
Question 26.
Explain briefly the steps in the construction of a consumer price index number.
Answer:
The following are main steps in the construction of consumer price index number.
- Object and scope.
- Conducting family budget survey.
- Obtaining price quotations.
- Method of construction.
(a) Object and Scope: Decide the class of consumers for Which Index number is required to construct. As whether Index number is meant for government employees, merchants, farmers, etc., Also, the geographical location, as that of locality, city or town, or a community of people who are having the similar consumption pattern.
(b) Conducting family budget survey: A sample survey regarding the. average expenses of families on various items of consumption is conducted. In the survey, the information regarding commodities consumed by the families, the quality and the respective budget is collected. The items included are under the heads of (i) Food, (ii) Clothing (iii) Fuel and Lighting and (iv) Miscellaneous.
Each of these can be divided into smaller groups as food may be included wheat, rice, dhal, etc.,
(c) Obtaining price quotations: While constructing the cost of living Index number, retail prices of commodities are to be collected. The price lists are obtained from different agencies from different places, then they are averaged and these average prices are used in the construction of Index Number. Here price list of current period and base period should be collected.
(d) Methods of construction: There are two methods of construciton of consumer price Index Number

![]()
Question 27.
What are simple and weighted Index Numbers?
Answer:
Value I.NO. V01 = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{0}}\) × 100\(\frac{1000}{800}\) × 1000 = 125
In Simple (unweighted) price Index numbers, an average of price relatives are calculated using Arithmetic mean and Geometric mean.
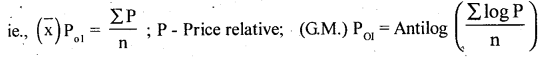
In Weighted price Index numbers appropriate weights are assigned to various items, and weighted average of price relatives are calculated using Arithmetic mean ad Geometric mean.
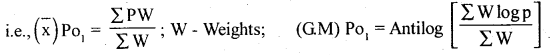
And Similarly, Simple and Weighted aggregative Index numbers are computed.
Question 28.
Explain the components of ‘time series’.
Answer:
The main components of time series are:
(a) Secular trend.
(b) Seasonal trend.
(c) Cyclical variations.
(d) Irregular/Random variations.
(а) Secular Trend: The term secular trend refer to the tendency of the variable to increase or decrease or remain steady over a period of time. Eg., the values of population, prices, sales, literacy, etc., are all increasing. As against the death rate, illiteracy, travel by bullock carts are decreasing. The rise or fall may be steep or gradual. But they show increasing trend, if we observe over a sufficiently long period of time (t > lyear).
(b) Seasonal Trend: The term seasonal variations basically refer to the seasons of the year- caused annually by the seasons of the year. But also includes the variations of any kind which are periodic in nature whose period is shorter than one year (t < 1 year). There are two important factors, which are responsible for seasonal variations, namely
(i) Climatic and wheather conditions
(ii) Customs, habits and traditions of the people.
For eg.,
- Sales of cool drinks, ice creams, are more in the summer season.
- Sales of stationery will be more in June-July.
- The business commercial bank may reach a peak around the first week of every month.
(c) Cyclical variations: Cyclical variations are fluctuations spread over a period of n.ore than one year. Most of the time series relating to economics and business show same kind of cyclical variations.
Hence cyclical variation is an oscillatory variation which occurs in four stages. Such as a) prosperity b) decline c) depression and d) Improvement.
Business cycle :
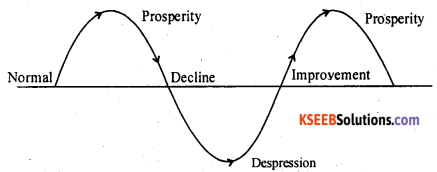
In prosperity the curve increases the depression business is in boom. After reaching the peak of activities the business declines the curve slopes down and is called period of decline. In depression the business activities are at the lowest. Then follows a period of nprovement and again reaches the properity. The interval of time from one prosperity to the other is called the period of cycle, (t > 1year)
(d) Irregular or Random variations: Irregular variations are those changes of time series, which are irregular in nature and donot show any pattern. The cause of irregular variations are due to accidental happenings such as wars, floods, earthquakes, famine, fire, strikes, etc., These factors being unpredictable. Generally such variations last for short period.
Question 29.
Use Newtons method to And the number of employees whose wages is ?500 perday.

Answer:
There are 5 known values of ‘Y’, so prepare leading difference table upto Δ4.


Question 30.
In a city 40% are vegetarians. In a random sample of 6 persons, find the probability that (i) 3 are vegetarians (ii) at least one is a vegetarian.
Answer:
Given : p = 40% = 0.4 q = 1 – p = 70.6 6n = 6
Let ‘x’ be the number of vegetarians is a Binomial variate with the parameters n = 6 p = 0.4 and q = 0.6, then,
The p.m.f. is –
p(x) = ncxpxqn – x; x = 0,1,2, …… n
= 6Cx (0.4)x (0.6)6 – 3; x = 0,1,2 ………… 6
(i) p(3 are vegetarians)
= p(x = 3) = 6C3 (0.4)3 (0.6)6-3 = 20 x 0.064 x 0.216 = 0.2765
(ii) p(atleast one is a vegetarian)
= p(x ≥ 1)= 1 – p(x < 1) = 1 – p(x = 0)
= 1 – 6C0 (0.4)0 (0.6)6-0 = 1 – 1 x 1 x 0.046 = 0,9554
![]()
Question 31.
The I.Q. of individuals in a population follows N.D. with mean 95 and SD 10. Find the probability of an individual having I.Q. a) less than 88, b) Between 88 and 108.
Answer:
Given µ = 95, σ = 10, .
Let x be the l.Q of individual is a Normal variate with the parameters µ – 95 and S.D= σ = 10. then S.NV.
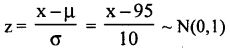
(i) p(IQ less than 88)
= p(x < 88)
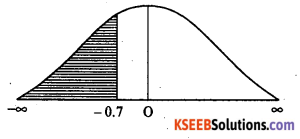
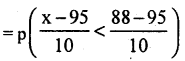
p(z < – 0.7)
= Area from O to (-∞) — Area from O to (- 0.7)
= 0.5 – 0.2580
p(x < 88) = 0.2420
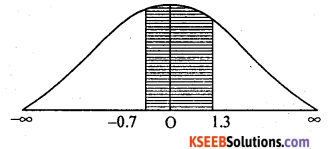
(ii) p(IQ between 88 and 108)
p (88 < x < 108)
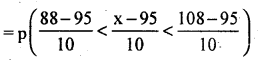
p(-0.7 < z < 1.3)
= Area from O to (-0.7)
= Area from O to 1.3 = 0.2580 + 0.4032
p(88 < x < 108) = 0.6612
Question 32.
A random sample of 600 oranges has a mean weight of 190 gms and S.D of 5gms. . Another random sample of 400 oranges has. a mean weight of 200 gms and S.D. 8 gms. Test whether the mean weights differ significantly at 0.01 level of significance.
Answer:
Given: n1 = 600, X̄1 = 190, S1 = 5
n2 = 400, X̄2 = 200, S2 = 8
α = 0.01
H0 : The means are equal
(i.e„ H0 : μ1, = μ2)
H1 : The means are not equal
(i.e„ H1 : μ1 ≠ μ2) …………….. (two tail test )
The test statistics is –
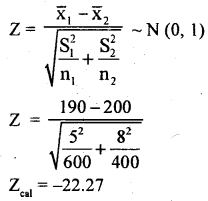
At α = 0.01 the two tail critical vales are -k1 = -2.58 and k2 = 2.58
Here Zcal is not lies between -k1, and k2/Zcal is in rejection region .
.’. H0 is rejected and H1 is accepted.
Conclusion : Means differ significantly.
Question 33.
The Following table gives the classification of 100 workers according-to sex and nature of work. Test whether nature of work is independent of sex of the worker.
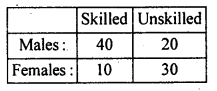
Answer:
H0 : The nature of work is independent of the sex of the worker.
H1 : The nature of work is dependent of the sex of the worker. {Upper/Right tail test}
The 2 x 2 contingency table is –
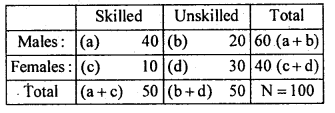
The statistic is –
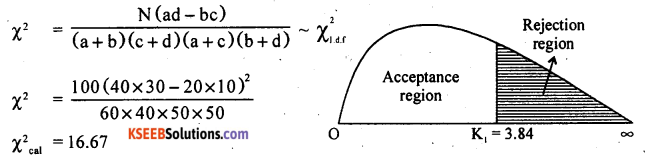
At a = 5% the upper Tail critical value for 1 d.f. is k = 3.84
Here χ2cal > k
∴ H0 is rejected and H1 is accepted.
Conclusion : Nature of work is dependent on the sex of the worker.
Question 34.
Solve the following game using dominance principle.
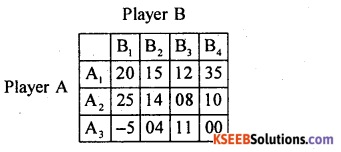
Answer:
By principle of dominance, in the pay off matrix, each pay – off in the first row exceeds the corresponding pay-off in the third row.
So, A1 dominates A3 and so, delete A3.
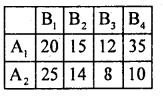
Here B3 dominates B1, B2 and B4 and so delete B1, B2, B4
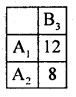
A1 dominates A2 delete A2
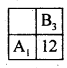
Thus saddle point occurs and (1,3)
The solution is:
- strategy for A is A1;
- strategy for B is B3;
- value of the game v = 12
Question 35.
An engineering company has a machine whose purchase price is Rs. 80,000. The expected resale value and expected maintenance cost in different years are as given below :

Determine the optimal age of replacement of the machine.
Answer:
Here p = Rs. 80,000. Let Ci and Sn be the maintenance cost and resale value.
Then total annual cost: T = (p – Sn) + ΣCi
Annual average cost [A(n)] = \(\frac{\mathrm{T}}{\mathrm{n}}\)
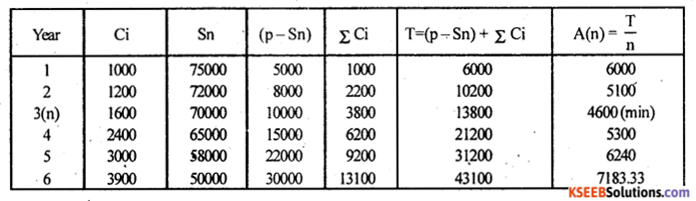
Here, Annual average cost A(n) is minimum for n = 3 years. Therefore the optimal age of replacement of the machine is n = 3 years.
Minimum average cost A(n) = A(3) = Rs. 4600.
Question 36.
During an examination of 10 pieces of equal lengths of cloth, the number of defects observed are : 2, 3, 4. 0, 5, 6, 7, 4, 3, 2 construct a suitable control chart and comment on whether the process is under control or not.
Answer:
Here number of defects are given, so, use c-chart and standards are not given.
Let, C – number of defects and K – sample number
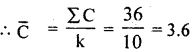
The control limits for c – chart are:
C – L = C̄ =3.6
L.C.L = C̄ – 3√C̄ = 3.6 – 3 √3.6 = -2.69 = taken as 0.
U.C.L = C̄ + 3√C̄ =3.6 + 3 √3.6 = 9.29
The c-chart are :
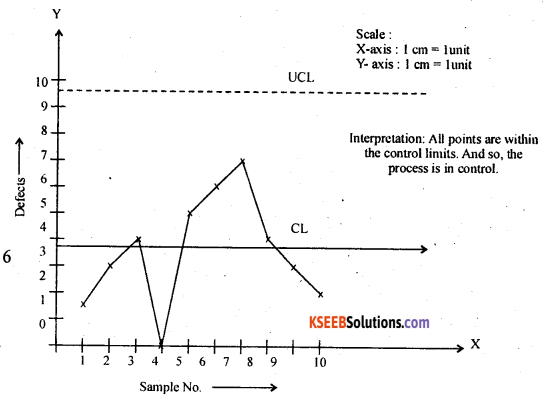
Interpretation: All points are within the control limits. And so, the process is in control.
![]()
Section-D
IV. Answer any TWO of the following Questions. 2 x 10 = 20
Question 37.
Construct Dorbish-Howley’s, Marshall-Edgeworths and Fishers’s price indent numbers from the following data and verify that fisher’s index number satisfies TRT and FRT.
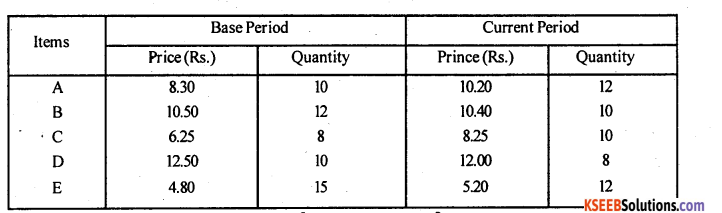
Answer:

Fishers Index satisfies FRT
Question 38.
(a) In a randomly selected corporation school, out of 80 students, 35 students passed S.S.L.C. examination with a first class. At 0.05 level of significance can we conclude that on an average 50% of the students in corporation school secured first class.
Answer:
Given: n=80; x=35
∴ p = \frac{x}{n}=\frac{35}{80} = 0.4375
p0 = 0.5 ∴ Q0 = 1 – P0 = 0.5. α = 5%
H0: proportion of first class secured students is 50% (0.5)
(i.e., H0 : p0 = 0.5)
H1 : proportion of first class secured students differ from 50% (0.5)
(i.e., H1 : p0 ≠ 0.5) {Two Tailed test)
The test statistics is –
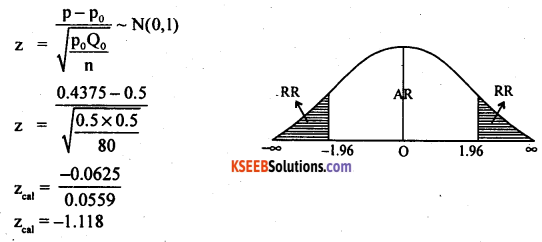
At α = 5% the two Tail critical values are -k1 = -1.96 and k2 = 1.96
Here zcal is in between -k1, and k2/zcal is in acceptance region.
∴ H0 is accepted.
Conclusion : Proporion of first class secured students in corporation school is 50% (0.5)
(b) Calculate standardised death rates for the following data. Determine more healthier town, taking town A as standardised population.
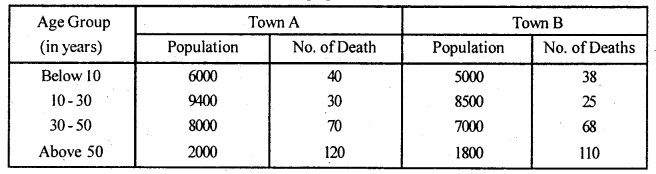
Answer:
Since town A population is taken standard (p) so, compute SDR(A) = CDR(A)
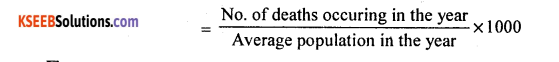
And SDR(A) = \(\frac{\sum \mathrm{PB}}{\Sigma \mathrm{P}}\)
B – ASDR’s of Town B
p – standard population
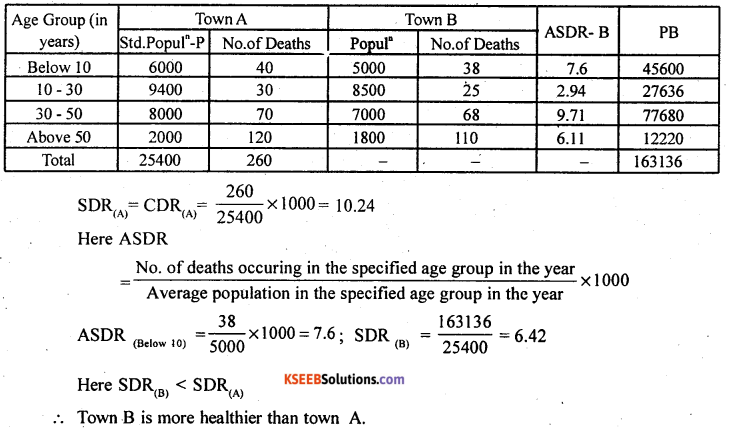
![]()
Question 39.
(a) The time taken by the workers while performing a job by method I and method II is given below:

Do the data show that the means of time distribution of populations from which these samples are drawn, do not differ significantly?
Answer:
Here n1 = 5, n2 = 6 (small samples n1/n2 < 30)
H0: means do not differ significantly.
(i.e., H0 : µ1 = µ2 )
H1 : means differ significantly.
(i.e., H1 : µ1 ≠ µ2 ) [Two Tail test]
The test statistic is –

tcal = -4
At α = 5% for (n1 + n2 – 2) = (5 + 6 – 2) = 9d.f and the two Tail critical values are -k1 = -2.26 k2 = 2.26
Here tcal = -k1 < tcal is not lies between -k1, and k2
∴ H0 rejected and H1 is accepted.
Conclusion : Means differs significantly.
(b) Calculate 3 yearly moving averages for the following data.

Answer:
Here m = 3,
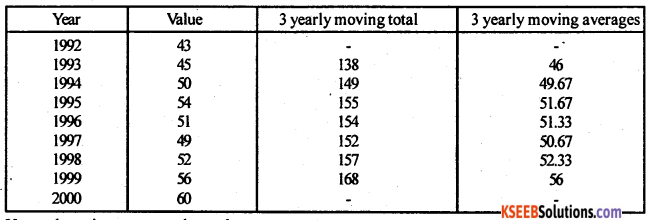
Here, there is an upward trend.
Question 40
Fit a poisson distribution to the following data and test for goodness of fit.

Answer:
H0 : Poisson distribution is a good fit to the observed data/distribution
H1 : Poisson distribution is not a good fit to the observed data/distribution.
To test H0 , we fit a poisson distribution to the data.
 src=”https://live.staticflickr.com/65535/49247611812_5ddf787aeb_o.png” alt=”2nd PUC Statistics Model Question Paper 1 with Answers – 45″ width=”358″ height=”407″ />
src=”https://live.staticflickr.com/65535/49247611812_5ddf787aeb_o.png” alt=”2nd PUC Statistics Model Question Paper 1 with Answers – 45″ width=”358″ height=”407″ />
The fitted poisson distribution is (Approx)
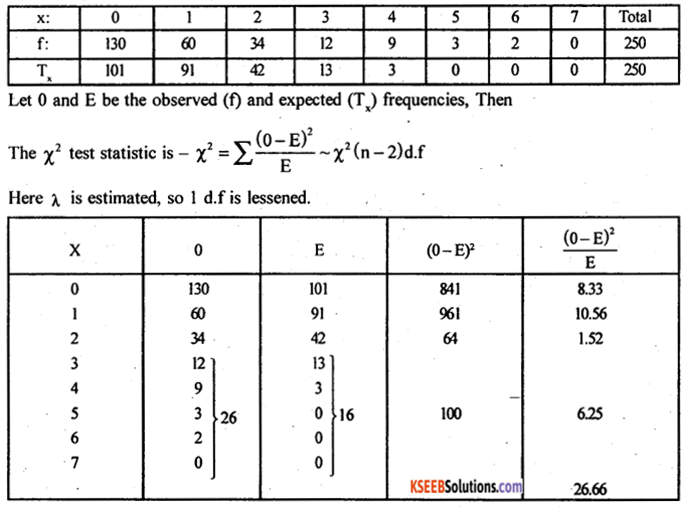
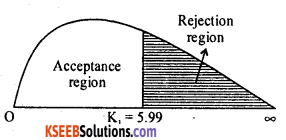
Here n = 4 . χ2cal = 26.66
At α = 5% the upper Tail critical value for (n – 2) (4 – 2) = 2 d.f is k = 5.99.
Here χ2cal > k.
∴ H0 is rejected and H1 is accepted.
Conclusion : Poisson distribution is not a good fit.
![]()
Section – E
V. Answer any TWO of the following questions.
Question 41.
A car hire agency has two cars. On an average there is a demand for one car during a particular hour. What is the probability that (i) both cars are free (ii) some demand is refused.
Answer:
Let X denote the number of cars hired / demond is a poisson variate with the parameter λ = 1. Then the p.m.f is –

(i) P(both cars are free)
= P (No cars are bired)
= p(x = 0) = \(\frac{\mathrm{e}^{-1} 1^{0}}{0 !}\) = e-1 = 0.3679
(ii) P (Some demand is refused)
= P(x > 2) = 1 – P (x ≤ 2)
[P(x = 0)+ P(x = l) + P(x = 2)]
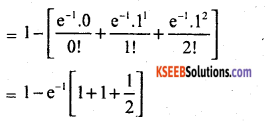
1 – 0.3679 x 2.5
= p (x > 2) = 1 – 0.9198 = 0.0802
Question 42.
Test the hypothesis that a = 5, given that sample standard devrection is 8 for random
sample of size 25 from a normal population use a = 0.05.
Answer:
Given : σ = 5, n = 25, s = 8, α = 0.05
H0 : σ = 5
H1 : σ ≠ 5(Two tailed test)
Under H0, the test statistic is : –


At α = 0.05 for (n – 1) = 25 = 1 = 24 d.f the two tail critical values are k1 = 13.85 and k2 =
Here χ2cal = 64 lies in Rejection region (RR)
∴ H0 is rejected and H1 is accepted
conclusion : σ ≠ 5
Question 43.
I.Q of 5 students before and after training our given below. Test whether the training is effective at α = 5%.
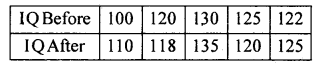
Answer:
H0 : I. Q. of students before and after training is same (i.e., µ1 = µ2 ) (Lower tailutest)
H1 : I.Q. of students has improved (µ1 = µ2). ; {Lower tail test}
Under H0, the test statistic is –
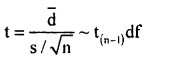
Let x and y be the I.Q. before after training
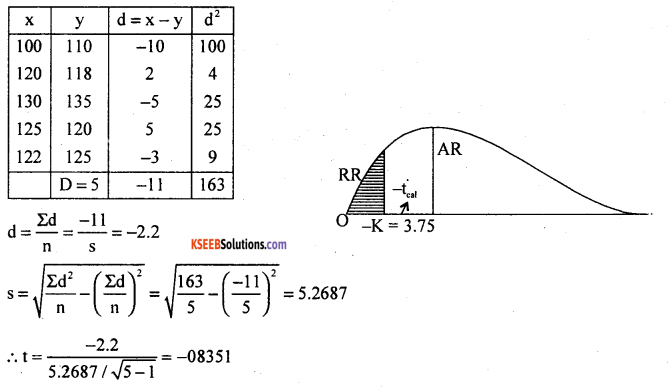
t cal =0.8351
At α = 5.1 for (n – 1) = 5 – 1 = 4 d.f the lower tail critical value -k = -3175
Here tcal lies in acceptance region (AR)
∴H0 is accepted conclusion : µ1 = µ2
Question 44.
Maruthi udyeg company purchases 10,000 rear mirrors for its cars annually. Each mirror costs ?180. The ordering cost per order is 12 and annual inventory carrying cost is 12% of capital cost. Find EOQ and minimum average inventory cost.
Answer:
Given : R = 10,000/year, P = 180, C3 = 12
12
I = 12% ; ∴C1 = PI = 180 x 12% = \(180 \times \frac{12}{100}=21.6\)
shortages not allowed used EOQ model I
EC Q : Economic order anantity
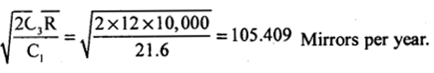
Minimum average inventory cost:
![]()