Students can Download 2nd PUC Statistics Model Question Paper 2 with Answers, Karnataka 2nd PUC Statistics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Statistics Model Question Paper 2 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 100
Note:
- Graph sheets and statistical tables will be supplied on request.
- Scientific calculators may be used.
- All working steps should be clearly shown.
Section – A
I. Answer any TEN the following questions. 10 x 1 = 10
Question 1.
Define Vital Statistics.
Answer:
Vital statistics is the science applied to the analysis and interpretation of numerical facts regarding vital events occurring in a human population.
Question 2.
What is the value Index number?
Answer:
Value index number indicates the effect of combination of price and quantity changes in between two time periods.
Question 3.
Write the formula of Dorbish Bowley’s price Index number.
Answer:
Dorbish-Bowley Price Index number is –
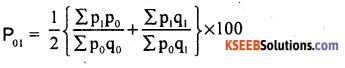
Question 4.
What do you mean by components of time series?
Answer:
The factors which are responsible for the fluctuations/ variations in the time series are called components of time series.
![]()
Question 5.
In which probability distribution mean and variance are equal?
Answer:
In poisson distribution mean and variance are equal i.e., mean (λ) = variance (λ).
Question 6.
Define S.N.V.
Answer:
A normal variate with mean μ = 0 and SD( σ) = 1 is called S.N.V. It is denoted by Z.
i.e., Z = \(\frac{x-\mu}{\sigma}\) ~N(0, 1)
Question 7.
What is the type I error?
Answer:
Type I error is taking a wrong decision to reject the null hypothesis (H0) when it is actua ly true.
Question 8.
Define Standard error.
Answer:
The standard deviation of the sampling distribution of sample statistic is called standard error.
Question 9.
Define critical region.
Answer:
The set of those values of the test statistic which lead to the rejection of the null Hypothesis is called critical region, also called as rejection region.
Question 10.
In a transportation when do you say that a solution is degenerate?
Answer:
The number of positive allocation in a basic feasible solution (B.F.S) is less than (m + n – 1), then the solution is called to be degenerate.
Question 11.
What is mixed strategy in a 2 person – zero – sum game?
Answer:
While playing a game, mixed strategy of a player is his pre-decision to chose his course of action according to certain pre-assigned probability.
![]()
Question 12.
What is lead time?
Answer:
Lead time is the time gap between placing order and arrival of goods at the inventory.
Section – B
II. Answer any TEN of the following questions. ( 10 x 2 = 20 )
Question 13.
The woman population of child bearing age group in a certain locality is 100000. The number of live births in the year in the locality is 2300. Find G.F.R.
Answer:

Question 14.
Define consumer price index number.
Answer:
Consumer price index number is the index number of the cost met by a specified class of consumers in buying a basket of goods and services.
Question 15.
Mention any two uses of analysis of Time Series.
Answer:
Analysis of time series is useful to
- Understand the past behaviour of the data.
- Predicting the future trend.
Question 16.
Write the normal equation for fitting the linear trend.
Answer:
na + bΣx = Σy
aΣx + bΣx2 = Σxy
Question 17.
Write any two assumptions of interpolation and extrapolations.
Answer:
- There are no sudden jumps in the values of dependent variable from one period to another.
- There will be no conscutive missing values in the series.
Question 18.
State under what conditions Binomial distribution tends to Poisson distribution.
Answer:
Binomial distribution tends to poisson distribution under the following conditions:
- When n is large i.e., n → ∞
- P is very small i.e., p → 0 and
- np = λ is fixed.
Question 19.
What are the value of β1, and β2 in Normal distribution?
Answer:
In Normal distribution, β1 = 0 and β2 = 3.
![]()
Question 20.
Define level of significance and critical value.
Answer;
- Probability of occurence of Type I error is called level of significance (α).
- The value of test statistics which separates the critical region (i.e., rejection region) and acceptance region is called critical value (k).
Question 21.
What are the conditions under which chi-square test of goodness of fit is applied?
Answer:
- The total frequency N should be large.
- The expected frequencies (E) should be 5 or more. If any E is less than 5, it should be pooled with adjacent frequency.
- If any parameter is estimated, one degrees of freedom should be lessened.
Question 22.
When no solution and unbounded solutions existed in L.P.P.?
Answer:
No solution exists in L.P.P. when the feasible solution does not exists.
Unbounded solution exists in L.P.P. when the feasible region is not unbounded or the optimum value of ‘z’ may be infinity.
Question 23.
What do you mean by replacement problems?
Answer:
Replacement problem is the problem of deciding the age at which the old equipments are replaced.
Question 24.
Define Setup cost and Holding cost.
Answer:
It is the cost of setting up of machines for production or the cost of placing the order for the goods.
It is the cost of carrying or holding the goods in stock until the goods are sold o used.
Section – C
III. Answer any EIGHT questions. ( 8 x 5 = 40 )
Question 25.
Write down the any two difference between CBR and GFR with respective formula.
Answer:
| CBR | GFR |
| a. It takes into consideration of the whole population | a. It takes into consideration of the women population of childbearing age. |
| b. It does not give importance to age and sex composition of the population. | b. It give importance to sex but not age composition of the population. |


Question 26.
Explain brielfy the steps involved in the construction of price Index number.
Answer:
The following are the steps/stages/principles/Heads involved:-
- Purpose and the scope
- Selection of base period
- Selection of commodities or itsm
- Selection of price list
- Selection an average Selection of weights
- Selection of formula
![]()
Question 27.
Construct cost of living Index number using a suitable formula and interpret it.
Answer:

Here price Index = p and expenditure = w
∴ Use family budget method.
(CPI) I01 = \(\frac{\sum p w}{\sum w}\)
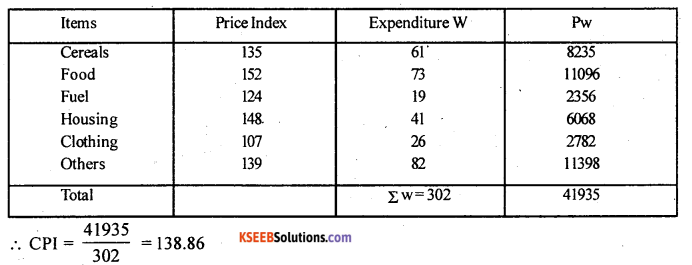
Question 28.
A Bernoulli variate with parameter p = 0.4, then find the probability for x = 1 and write down mean and variance.
Answer:
Given : p = 0.4, ∴ 1 – p = 1 – 0.4 = 0.6
Then p(x = 1) = (0.4)1 (1 – 0.4)1-1 = 0.4 x 0.60 = 0.4
Mean p = 0.4, variance = p( 1 – p) = 0.4 x 0.6 = 0.24.
Question 29.
Estimate the sale of a business concern for the year 2012.
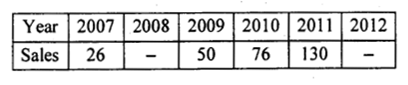
Answer:
Let X and Y be the year and sales.

There are four known values of y. So, using binominal expansion;
(y-l)4 = 0 : y4<-4y3 + 6y2-4y1 + yo = 0 ……….. (1)
130-4 (76)+ 6(50)-4 y1 + 26 = 0
130-304 +300-4y1 + 26 = 0
152 – 4y1 = 0 ∴ -y1=\(\frac{-152}{4}\) y1 = 38
Rewrite equation (1) by increasing suffixes of by ‘ 1’ we get y5
y5 – 4y4 + 6y3 – 4y2 + y1=0
y5 – 4(130) + 6(76) – 4(50) + 38 = 0; Since y1 = 38
y5 – 520 + 456 – 200 + 38 = 0
∴ y5 = 226.
Question 30.
In a college 40% are girls. In a random sample of 5 students, find the probability of getting,(i) 2 girls (ii) at least 3 girls.
Answer:
Let x be the number of girls is a Binomial variate with the parameters n = 5,
p = 40% = 0.4. ∴ q = 1 – p = 0.6.
The p.m.f. is –
P(x) = ncx px qn – x; x = 0,1,2, …… n
= 5cx (0.4)x (0.6)5-x; x = 0,1,2, …….. 5
(i) p(2 are girls) = p(x = 2) = 5C2(0.4)2(0.6)5-2
=10 x 0.16 x 0.216
= 0.3456
![]()
(ii) p(atleast 3 girls) = p(x ≥3)
=p(x = 3) + p(x = 4) + p(x = 5)
= 5C3 (0.4)3(0.6)5-3 + 5C4(0.4)4(0.6)5-4+ 5C5(0.4)5(0.6)5-5 = 10 x 0.064 x 0.36 + 5 x 0.0256 x 0.6 + 1 x 0.01024 x 1
= 0.2304 + 0.0768 + 0.01024
p(x ≥ 3) =0.3174.
Question 31.
A Factory has produced 10,000 electric bulbs. Assuming that the expected life of these bulbs is Normally distributed with mean 120 days and S.D. 20 days. Find the number of bulbs which will burn (i) before 90 days (it) between 80 and 140 days.
Answer:
Let ‘x’ be the life of bulbs is a Normal variate with mean µ = 120 and S.D. σ = 20 days, then,
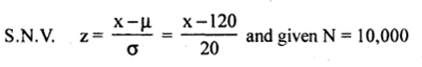
(i) p(bulb burn before 90 days)
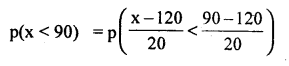
= p(z < -1.5)
= Area from (-1.5) to (-∞)
= Area from 0 to (-∞) – Area from 0 to (-1.5)
p(x < 90) = 0.5 – 0.4342 = 0.0658
∴ Number of bulbs bum before 90 days
= p(x < 90) x N
= 0.0658 x 10000 = 658
(ii) p(bulb bum in between 80 and 140 days)
= p(80<x< 140)
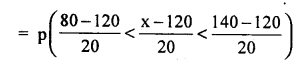
= p(-2 < z < 1) .
= Area from (-2) to 1
= Area from 0 to (-2) + Area from 0 to 1
p(80 < x < 140) = 0.4772 + 0.3412 = 0.8185
∴ Number of bulbs bum in between 80 and 140 days
= p(80 < x < 140) x N
= 0.8185 x 10,000
= 8185.

Question 32.
A random sample of 100 jack fruits weigh on an average 10 lbs. With variance of 41 lbs2. Test at 1% level of significance that the expected average weight of jackfruits of that varieties is 11 lbs.
Answer:
Given : n = 100, X̄ = 10 lbs. S2 = 41 lbs2, ∴ S = 6.4 lbs, μ = 11 lbs.
H0 : Average weight of Jack fruits is 11 lbs.
(i.e., H0 : μ = 11lbs)
H1: Average weight of Jack fruits differ from 11 lbs.
(i.e., H1 : μ ≠ 11lbs) { Two Tail test }
The test statistics is –
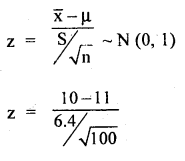
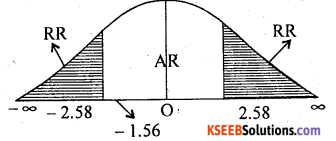
ZCal = -1.56
At α – 1% the two Tail critical values are -k1 = -2.58 and k2 = 2.58. .
Here zcal lies between k1 and k2.
∴ H0 is accepted.
Conclusion: The average weight of Jack fruit is 11 lbs.
Question 33.
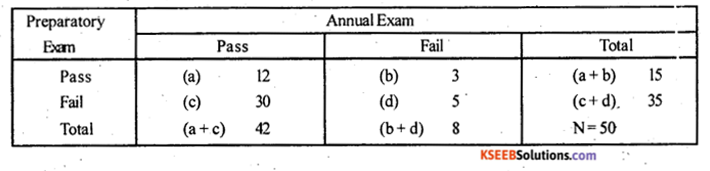
In a college there were 50 students in II pu commerce. Among them 15 students . passed in preparatory examination. Whereas in annual examination 42 students passed. However among those who passed in the preparatory examination only 12 students passed in the annual examination. Test at 1% level of significance whether passing in the preparatory examination and passing in the annual examination are independent.
Ans.
H0 : Pass in Preparatory and pass in annual examination are independent
H1 : Pass in preparatory and passes in annual examination, are not independent.
The 2 x 2 contingency table is:
Here one of the class frequency at b = 3, is less than 5, so, apply Yate’s correction.
The test statistic is –
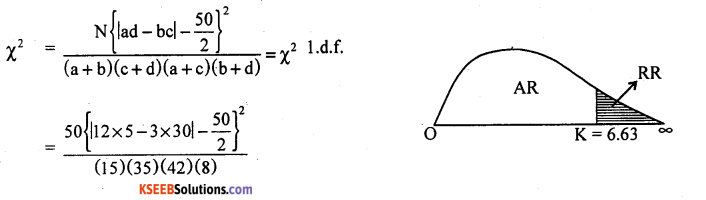
χ2 = 00071
At a = 1% the upper Tail critical value for 1 d.f. k = 6.63 Here
χ2cal < K .
H0 is accepted
Conclusion Pass in preparatory and pass in annual examination are independent.
![]()
Question 34.
Solve the following game using principle of dominance.
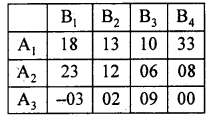
Answer:
By principle of dominance, in the pay off matrix, each pay off in the first row exceeds the corresponding pay-off in the third row.
A1 dominates A3,
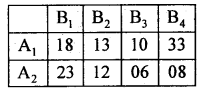
Here B3 dominates B1, B2 and B4 and so delete B1, B2 and B4.
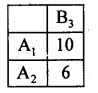
A1 dominates A2, delete A2.
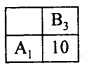
Thus saddle point occurs at (1, 3)
The solutions –
- Strategy for A is A1
- Strategy for B is B3
- Value of the game v = 10
Question 35.
An engineering company has a machine whose purchase price is Rs. 7000. The expected maintenance cost £nd resale values in different years are given below:

When should the machine be replaced?
Answer:
Here p = 7000, let Ci and Sn be the maintenance cost and resale value, then,
Total annual cost: T = (p – Sn) + ΣCi and
Annual average cost: \(A(n)=\frac{T}{n}\) ; n = years
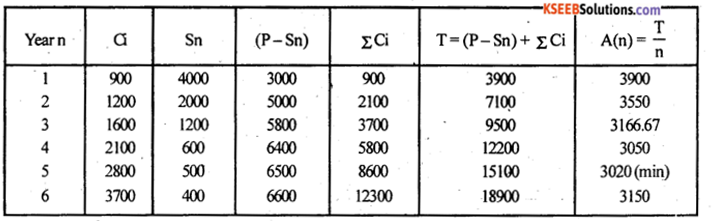
Here, annual average cost A(n) is minimum for n = 5 years. Therefore the optimal replacement age is n = 5 years. The is machine should be replaced for every 5 years.
Minimum average cost: A(5) = Rs. 3020.
Question 36.
Glass panes are manufactured by a firm. Broken corner, excessive thickness, excessive colour tint are considered defect. The number of defects in randomly selected panes are noted as below :

Draw chart for defects and analyse the data.
Answer:
Here, number of defects are given, so use c-chart, standards are not given.
Let C and K be the number of defects and sample number.
\(\bar{c}=\frac{\Sigma c}{K}\)
= \(\frac{23}{8}=2.875\)
The control limits for c-chart are :-
C.L. = C̄ =2.875
L.C.L. = C̄ – 3√C̄ = 2.875 – 3 >/2.875 . ;
= -2.211 ≅ 0 (Taken as 0)
V.C.L. = C̄ + √C̄
= 2.875 + 3√2.875
= 7.961
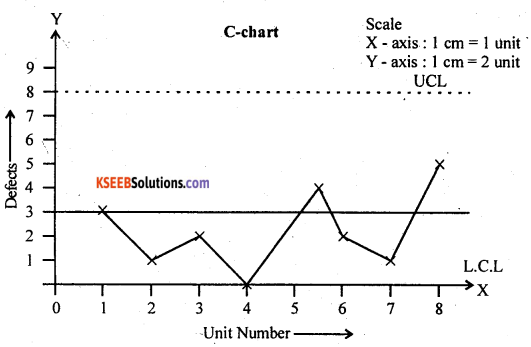
Interpretation:
All the points are within the control limits. And so, the process is in control.
Section – D
IV. Answer the following Questions
Question 37.
Calculate Fisher’s and Dorbish-Bowley’s Index numbers and test whether they satisfies T.R.T and F.R.T.
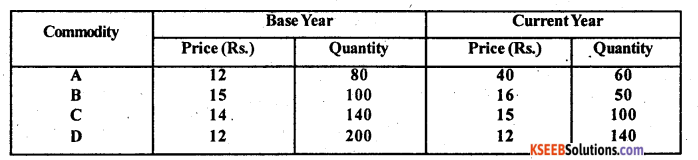
Answer:


∴ Fisher’s Index number satisfies T.R.T.
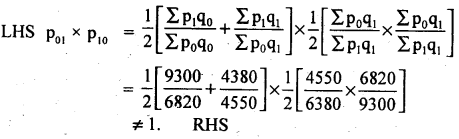
Dorbish – Bowely Index number does not satify T.R.T.

Dorbish – Bowely’s :
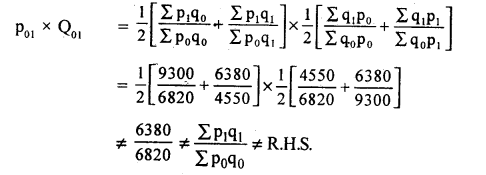
∴ Dorbish – Bowely Index number does not satisfy T.R.T.
![]()
Question 38.
(a) In a college, out of 60 students randomly selected 40 passed in II PU examination in first class. At 5% level of significance can we conclude that on an average 50% of the students in the college pass in first class.
Answer:
Given: n = 60, x = 40, ∴ p = \(\frac{x}{n}=\frac{40}{60}\) = 0.67
p0 ∴ q = 1 – p0
H0 : The proportion of first class pass students ¡s 0.5
(i.e., H0 : p0 = 0.5)
H1 : The proportion of first class pass students differs from 0.5; {Two Tail test)
(i.e., H1 : p0 ≠ 0.5) .
The test statistic is –

z cal = 2.63
At α = 5% the two Tail crtitical values are -k1 = 1.96 and k2 = 1.96.
Here zcal is outside the interval -k1 and k2 /zcal is in rejection region.
∴ H0 is rejected and H1is accepted.
Conclusion : The proportion of first class pass students differs from 0.5
(b) Calculate standardised death rates. Which population seems to be healthier ?
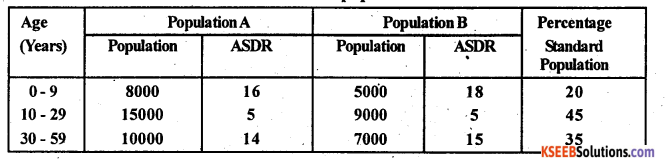
Answer:
Let A and B be ASDR’s of population A and B and P be the standard population.
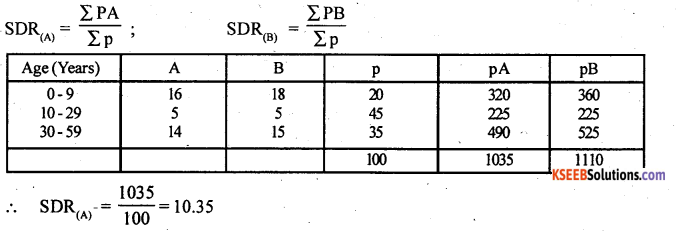
SDR(A) = \(\frac{1110}{100}\) =11.10
SDR(A) < SDR(B)
Population A is healthier than population B.
Question 39.
(a) From the following data, test whether mean life of brand B bulbs are longer than that of brand A bulbs.

Answer:
Here n1 and n2 are less than 30, So, use small sample test.
Given: n1 = 12, n2 = 15
X̄1 = 1240 X̄2 = 1370
S12 = 1000 ,S22 = 2000
H0 : Mean life of Brand A and Brand B bulbs are same.
(j.e., H0 . µ1 = µ2)
Mean life of Brand B bulbs are-longer than Brand A bulbs.
(i.e., H1. µ1 < µ2) {Lower/Left Tail test}
The test statistic is –
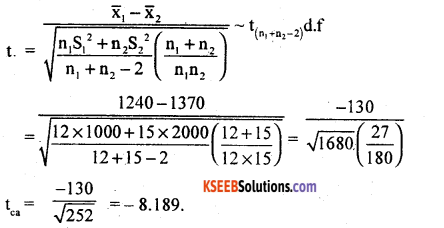
At α = 5% the left Tail crtitical value for (n1 + n2 – 2) = (12 + 15 – 2) = 25 d.f. (from t-table values is -k = -1.71
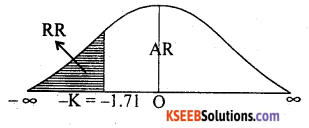
Here tcal = -8.189 is in rejection region/ .tcal< -k.
∴ H0 is rejected and H1 is accepted.
Conclusion: Mean life of Brand B bulbs are longer than Brand A bulbs,
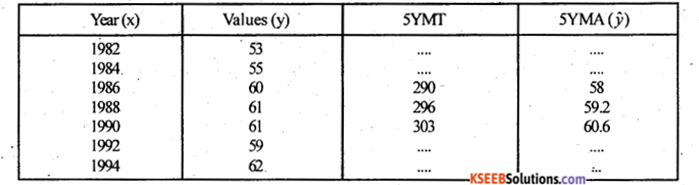
(b) Calculate 5 yearly moving averages for the following data :

Answer:
Competitive of 5 yearly moving average m = 5
Question 40.
The following table shows the number of defective blades in, each packet of 5 each.

Test whether Binomial distribution is a good fit to this observed data.
Answer:
The null hypothesis is
H0 : Binomial distribution is a good fit to the observed data.
H1 : Binomial distribution is not a good fit to the observed data.
To test H0, we fit Binomial distribution to the data.
The parameter ‘p’ is estimated by finding mean.
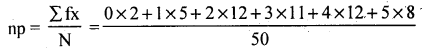
Here let x and f be the no. of defectives and number of packets.
5p = \frac{150}{50} = 3
∴ p = \frac{3}{5} = 0.6 ∴q 1 – p = 0.4
The p.m.f is
p(x) = ncx px qn – x; x = 0,1,2, …… n
= 5cx 0.6x 0.45 – x; x = 0,1,2, …… n
Theoretical frequency : Tx = p(x) x N
T0 = (x=0) x 50 = 5C0 (0.6)0 (0.4)5-0 x 50
T0 = 0.512
Using recurrence relation of theoretical frequency

Thus the fitted Binomial distribution is (Approx)

Then the test statistic is
Here one parameter ‘p’ is estimated from the data.
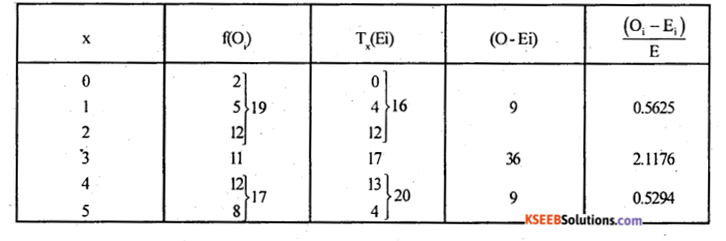
Here first two and last one theoretical frequencies are less than 5. Therefore they are pooled with the adjacent frequencies such that they are 5 or more.
χ2cal = 3.2095
At α = 5% the upper tail critical value for (n – 2) = (3 – 2) = 1 d.f. is k = 3.84
Here χ2cal < k.
∴ H0 is accepted.
Conclusion: Binomial distribution is good fit to the observed data.
![]()
Section – E
V. Answer any TWO of the following questions. ( 2 x 5 = 10 )
Question 41.
If 98% of electric bulbs manufactured by a company are known to be non-defective. What is the probability that a sample of 150 electric bulbs taken from the meduction process from the company, what would contain (i) Exactly on detective electric bulbs (ii) More than twe detective electric bulbs?
Answer:
Let x denote number of detective electric bulbs is a binomial variate with the parameters n = 50 q = 98% are non-defective P = 1 – 9 = 2% = 0.02 are detectives.
Here n is very large and P is very small under these condition it tends to poisson distribution with the parameter λ = np = 150 x 002 ,
λ = 3
Then the p.m.f of poission distribution is

(i) P (exactly one defective bulb)
P(x = 1) = \(\frac{e^{-3} \cdot 3^{1}}{11}\) = e-3.3= 0.0498 x 3 = 0.1494
(ii) P (More than two detective bulbs)
= P (x > 2)
= 1 – P(x ≤ 2)
= 1 – [P(x = 0)+P(x = 1 )+P(x = 2)]
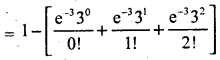
= 1 – e-3 [1 + 3 + 4.5] = 1 – 0.0498 x 8.5
P(x > 2) = 1.04233 = 0.5767.
Question 42.
A normal variate has variance 8 – twenty sample observations of the variate have variance 9. Test at 1% level of significance whether the population variance is 8.
Answer:
Given ; σ2 = 8, n = 20, s2 = 9. α = 1%
H0: Population variance is 9. (H0: σ2 = 8)
H1 : Population variance differs from 9. (H, : σ2≠ 8); (two tailed test)
Under H0, the χ2 – test statistic is : –
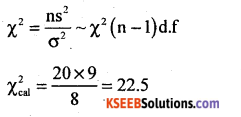
Here χ2cal lies in acceptance region
.’. H0 is accepted
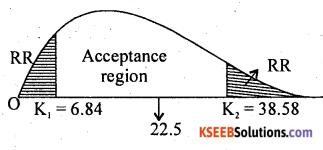
Conclusion: σ2 = 8
Question 43.
The marks obtained by 5 students before and after attending coaching classes were given below. Test whether coaching was useful (use α = 1%).

Answer:
Given : n1= n2 = n = 5.
Let x and y be the marks before and after attending coaching class and let d = x – y.
H0: Mean marks before after coaching are same.
(i.e., H0. µ1 = µ2)
H, : Mean marks after attending coaching are more (i e., 11, :p,<ft2)
(i.e., H0. µ1 < µ2)
The test statistic is –
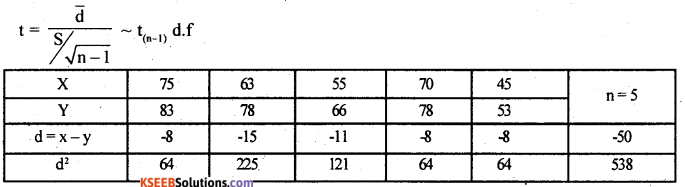
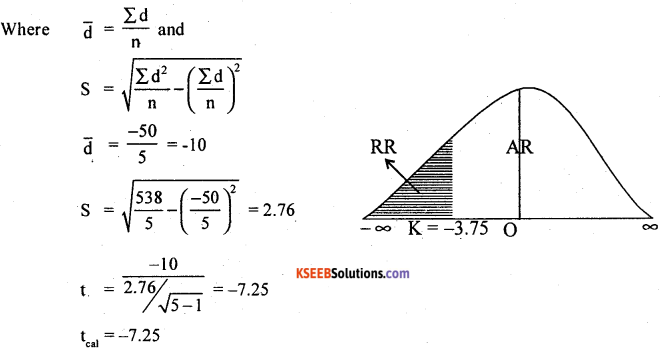
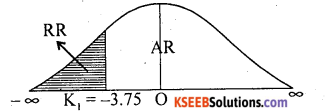
At α = 1% the lower Tail critical value for (n – 1) = (5 – 1) = 4. d.f; -k = —3.75
Here tcal < k
H0 is rejected and H1 is accepted.
Conclusion: Coaching is not useful.
![]()
Question 44.
Find the initial feasible solution to the transportation problem given below by North west corner rule.
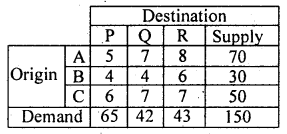
Answer:
Since total supply (70 + 30 + 50) = total demand (65 + 42 + 43). The problem is said to be balanced T.P.
By N.W.C.R
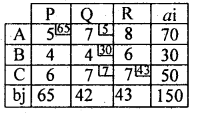
First allocation is made at North West corner cell at (1,1) as : X11 = min (70, 65) = 65
Here P is satisfied and so, allocate at the cell (1, 2) as : X12 = min (70, 65, 42) = (5, 42) = 5
Here A is satisfied, next allocation is made at the cell (2, 2) as :
X22= min (30,42 – 5)
= min (30, 37) = 30
B is satisfied allocate at (3, 2) as
X32
= min (50, 42 – 35)
= min (50, 7) = 7
Here Q is satisfied Next allolate at (3, 3)
as : X33 = min (50 – 7, 43) = min (43, 43) = 43
So, all availabilities (ai) and requirements (bj) are satisfied
The total transportation cost is
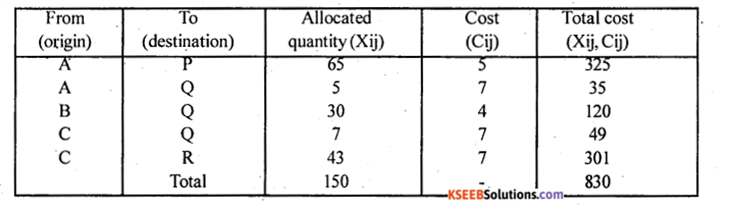
The total transportation cost = 830 is the intitial besic feasible solution.