Students can Download 2nd PUC Statistics Model Question Paper 3 with Answers, Karnataka 2nd PUC Statistics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Statistics Model Question Paper 3 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 100
Note:
- Graph sheets and statistical tables will be supplied on request.
- Scientific calculators may be used.
- All working steps should be clearly shown.
Section – A
I. Answer any TEN the following questions. ( 10 × 1 = 10 )
Question 1.
Mention a source of vital statistics.
Answer:
Registration method/census method
Question 2.
What is the index number for the base year.
Answer:
Index number for the base year = 100.
Question 3.
Mention a use of index number.
Answer:
Index numbers are used in fixation of bank rates, grant of dearness allowance to employees
Question 4.
Give an example for ‘seasonal variation’ in time series analysis.
Answer:
Sales of cool drinks, ice creams are more in the summer season.
Question 5.
Mention a feature of Bernoulli distribution
Answer:
Bernoulli distribution has parameter – p or mean = p or variance = p (1 – p)
![]()
Question 6.
Write the relationship between mean and variance of Poisson distribution.
Answer:
Mean = variance
Question 7.
Define point estimation.
Answer:
In point estimation a single statistic is used to provide an estimate of the population parameter OR .while estimating unknown parameter if a special value is proposed as an estimate is called point estimation.
Question 8.
Write down the expression for SE(p)
Answer:
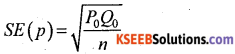
Question 9.
What is the degree of freedom used in test of goodness of fit when one of the parameter is estimated?
Answer:
Degrees of freedom = (n – 1 – 1 ) = (n – 2)
Question 10.
What is meant by multiple solution in a L.P.P?
Answer:
If an L.P.P. has many optimal solutions, it is said to have multiple solution.
Question 11.
What is meant by pure strategy?
Answer:
While playing a game, pure strategy of a player is his determined decision to adopt a specified course of action, irrespective of the course of action of the opponent.
Question 12.
What are control charts in S.Q.C?
Answer:
Control chart is a graphical device which is used to verify whether the production process is in control or not.
![]()
Section – B
II. Answer any TEN of the following questions. ( 10 × 2 = 20 )
Question 13.
Calculate I.M.R. for the following data.

Answer:
Infant Mortality Rate is
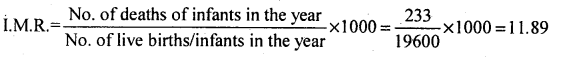
Question 14.
What are T.R.T. and F.R.T. in index numbers?
Answer:
T.R.T (Time Reversal Test) and F.R.T (Factor Reversal Test) are Reliability Tests used to choose an appropriate formula which satisfies these tests.
Here T.R.T : P01 × P10 = 1 ; and P01 × P10 = \(\frac{\Sigma P_{1} q_{1}}{\Sigma P_{o} q_{0}}\) (except 100)
Question 15.
Given P01(L) =125 and P01(P) = 122 find P01(DB) = 122.
Answer:
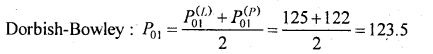
Question 16.
Mention a merit and demerit of moving averages method of measuring trend in a time series.
Answer:
Merit: The method is simple.
Demerit: The method does not provide trend values at the beginning and at. the end of the time series.
![]()
Question 17.
Expand (y – l)6.
Answer:
(y-l)6 = y6 – 6y5 + 15y4 – 20y3 +15y2 – 6y1 + y0 = 0
Question 18.
In a N.D. of Q1= 22 ems and Q3 = 34 ems then find median.
Answer:
In a normal distribution the two quartiles are equidistant from the median
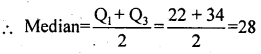
Question 19.
Find the area under the Normal curve to the right of z = 1.3.
Answer:
Area under normal curve to the right of z = 1.3
= Area from 0 to ∞ – Area from 0 to 1.3
=0.5 – 0.4032 = 0.0968
Question 20.
Mention any two features of t-distribution.
Answer:
(a) Range is ( -∞ , ∞ )
(b) Mean = 0 (mean = median = mode = 0).
Question 21.
Mention two application of tests.
Answer:
(a) To test whether a population has given variance.
(b) To test ‘goodness of fit’ of theoretical frequencies to a observed frequencies.
Question 22.
Mention two situations when replacement is carried out.
Answer:
Replacement’s carried out when
(a) Machine and their spare parts deteriorates with time.
(b) The maintenance cost increases and efficiency reduces.
Question 23.
Write the formula for minimum average cost in E.O.Q. model with shortages, giving meaning of notations.
Answer:
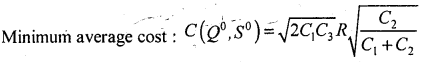
Here
C1 = carrying/ Holding/ Maintenance cost
C2 = Shortage/penalty cost per unit/unit time
C3 = set up cost/ capital cost .
R = Demand Rate
Question 24.
What is meant by defect and defectives in S.Q.C?
Answer:
A ‘defect’ is a quality characteristic which does not conform to specifications.
The presence of one or more defects in a product is ‘defective.
![]()
Question 25.
From the following data, calculate Total Fertitlity Rate.

Answer:
Total Fertility Rate.(T.F.R) =5 Σ Quinquennial ASFR’s

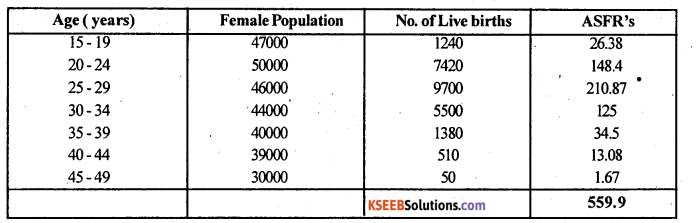
TFR = 5Σ Quinquennial ASFR’ = 5 × 559.9 = 2799.5
Section – C
III. Answer any EIGHT questions. ( 8 × 5 = 40 )
Question 26.
Explain steps while constructing consumer price index number.
Answer:
The following are main steps in the construction of cost of living index numbers.
(a) Object and scope.
(b) Conducting family budget survey.
(c) Obtaining price quotations.
(d) Method of construction.
(a) Object and scope:
Decide the class of consumers for which index number is required. Such as whether index number is meant for govt, employees, bank employees, merchants, farmers etc. Also the geographical location as that of city, town, or a community of people who are having the similar consumption pattern.
(b) Conducting family budget survey:
A sample survey regarding the average expenses of familities on various items of consumption is conducted. In the survey, the information regarding commodities consumed by the families, their quality and the respective budget is collected. The items included are under the heads of i) food (ii) clothing (ii) fuel and lighting and (iii) miscellaneous
Each of these can be divided into smaller groups as food may be include wheat, rice, dhal etc which are consumed by the people for whom index is meant.
(c) Obtaining price quotations:
While constucting the cost of living index number, retail prices of commodities are to be collected. The price lists are obtained from different agencies from different places. Then, they are averaged and these averages are used in the construction of index numbers. Here price lists of current period as well as base period should be collected.
(d) Methods of construction:
There are two methods of construction.
(i) Aggregative expenditure method (A.E.M)
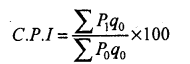
(ii) Family Budget Method (F.B.M).
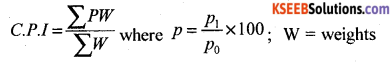
Price
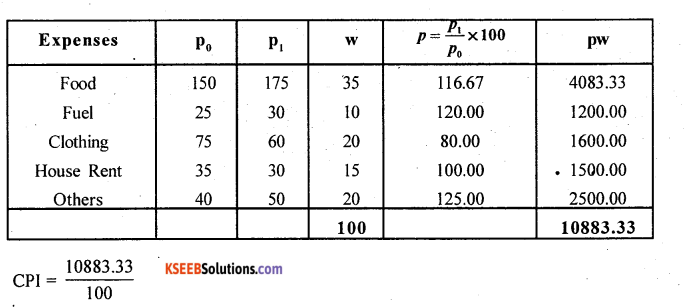
Question 27.
Calculate cost of living index number by family budget method.
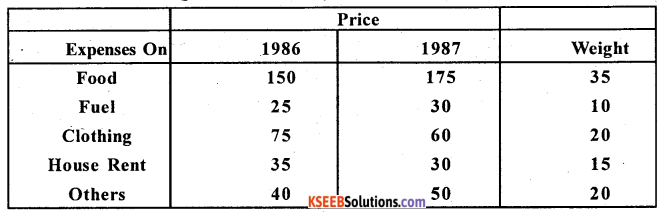
Answer:
Consumer price index number by family budget method = \(\frac{\sum p w}{\sum w}\) ; p = \(\frac{p_{1}}{p_{0}} \times 100\) ; w = Weights.
![]()
Question 28.
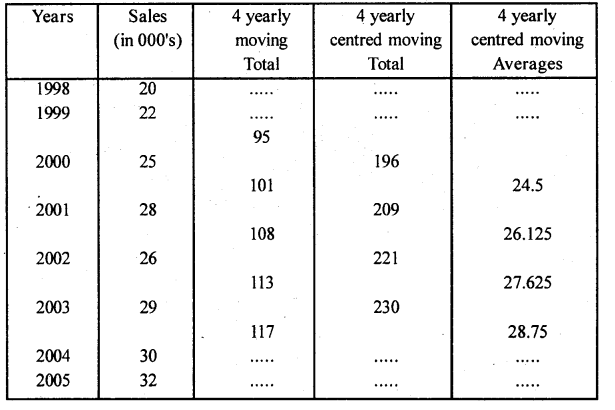
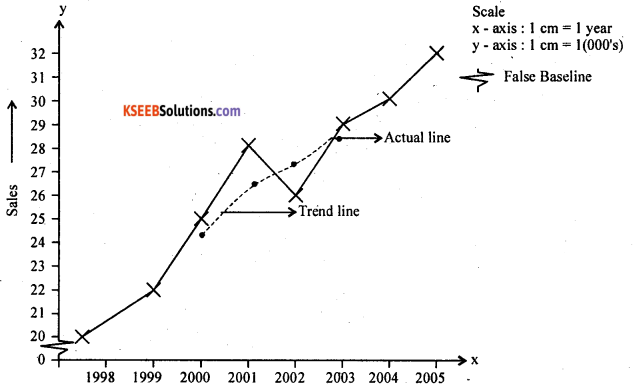
Obtain trend using 4 yearly moving averages method from the following data. Also plot original and trend values on a graph.

Answer:
Here m = 4
Question 29.
Use Newtons advancing difference method to find the value of y when x = 30.
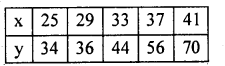
Answer:
Since the value to be estimate does not one of the data (x) series. So, apply Newton’s method. The number of known value of 4 are 5, prepare the leading difference upto Δ4.

Question 30.
The number of print mistakes per page in a text book follows P.D. with mean = 2. If there are 560 pages in a book, in how may pages would you expect mistakes?
Answer:
Let x be the number of mistakes per page in a text book is a Poisson variate with the parameter λ = 2 Then
The p.m.f is –
P(x) = \(\frac{e^{-i} \lambda}{x !}\) ;x = 0,1,2 ………….
The number of pages expect mistakes = P (there are mistakes) × N
= P(x ≥ 1) × N .
= 1 – p(x < l) × 5600
= {1 – P(x = 0)} × 5600
= |1 – 0.1353| × 5600 = 4842 pages
![]()
Question 31.
From the following data obtain theoretical frequencies, assuming p= 1/2 , for a.B.D.
imag 64
Answer:
Let X is a binomial variate with (P = q) the parameters p = \(\frac{1}{2}\) ;q = \(\frac{1}{2}\) and n = l
Then the p.m.f. is:
P(x) = ncx px qn – x; x = 0,1,2, …… n

Theoretical frequency Tx = P(x) × N
T(X = 0) = T0 = P(x=0) × 128
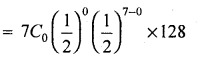
= 1 × 1 × 0.0078125 × 128
∴T0 = 1
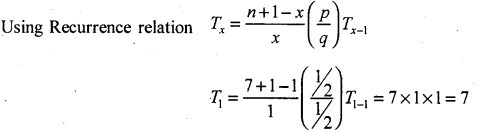
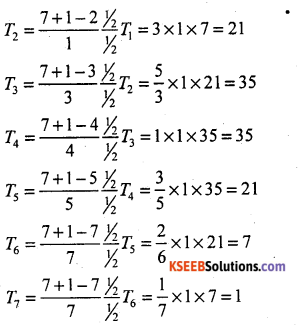
The fitted observed and theoritical frequency distribution is:

∴ Here the distribution is symmetric, since P = q = \(\frac{1}{2}\)
![]()
Question 32.
In a sample of 600 students of a college 400 are found to use dot pens. In another college from a sample of 900 students, 450 were found to use dot pens. Test whether the two colleges differ significantly with respect to the habit of using dot pens.
Answer:
Given n1 = 600, x1 = 400, ∴P1 = \(\frac{x_{1}}{n_{1}}-\frac{400}{600}=0.67\) .
n2 = 900, x2 = 450 ∴P2 = \(\frac{x_{2}}{n_{2}}-\frac{450}{900}\) = 0.5
H0 : The proportion of students using dot pens in the two colleges are same
(i.e. H2 : P01 = P02 = P0)
The proportion of students using dot pens in the two colleges are not same,
(i.e. H1 : P01 ≠ P02 = P0) (two tail test)
The test statistic is –
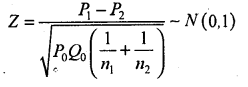

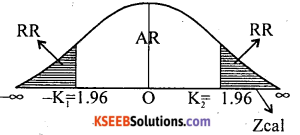
Zcal =6.5097
At α = 5% the two tail critical values are -k1:, =1.96 and k2 =1.96
Here Zcal is in rejection region / Zcal > K2 .
∴ H0 is rejected and H1 is accepted.
Conclusion : The proportion of students using dot pens in the two colleges are not same.
Question 33.
A manufacturer of tyres claims that average life is more than 15000 kms under normal condition. A random sample of 15 tyres was tested and mean and S.D. was found to be 18000 kms and 4000 kms respectively. Test whether the manufacturer’s claim is justified.
Answer:
Given: μ= 15000 kms, nj = 15, X̄ = 18000, s = 4000, α = l%
H0 : Average life of tyres is 15000 kms (i.e. H0 : μ = 15000)
H1 : Average life of tyres is more than 15000 kms
(H1 : μ >15000) {Right/upper tail test)
The t-test statistic is ( Here n < 30 use t -test for mean)
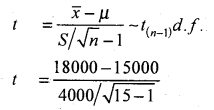
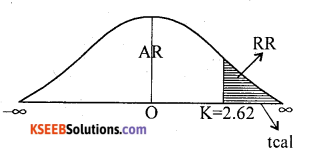
At α = 1 % for (n – 1) = (15 ) = 14 d.f. the upper tail critical value k = 2.62
Here t>cal > k/tcal is in rejection region.
∴ H0 is rejected and H1 is accepted.
Conclusion : Average life of tyres is more than 15000 kms.
Question 34.
Solve the L.P.P graphically
minimise Z = 3x + 24
subject to 5x + 4y ≤ 50
x + 2y ≥10
and x, y ≥ 0
Answer:
Consider the constraints and written as equalities and are represented by straight lines, by identifying two points on each of these lines.
5x + 4y = 50 put x = 0 we get y = 12.5 …………. (0,12.5)
put y = 0, we get x = 10 ………………. (10,0)
and x + 2y = 10 put x = 0 we get y = 5 (0,5)
put y = 0 , we get x = 10 (10,0)
The equations are graphically represented as below
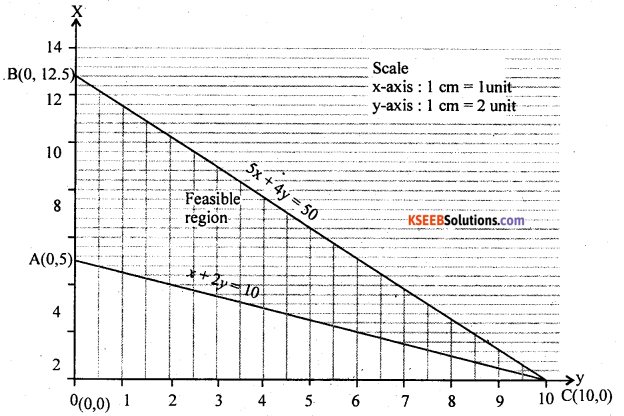
The corner points of the feasible region are
A(0,5), B(0,12.5) and C(10,0)
Consider the comer points
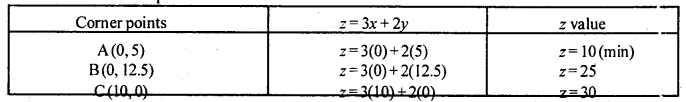
Since ‘Z’ is to minimize which occurs at A(0,5)
The optimum solution is x = 0, y = 5
The optimum value of z = 10
![]()
Question 35.
A firm is considering of replacing a certain equipment, whose purchasing price is Rs. 5,000, when should we do so?

Answer:
Here P = Rs. 5,000
Let Ci and Sn be running cost and resale value (Rs.)
Average annual cost A(n) = \(\frac{T}{n}\)
Her-s T = (p – Sn) + ΣCi
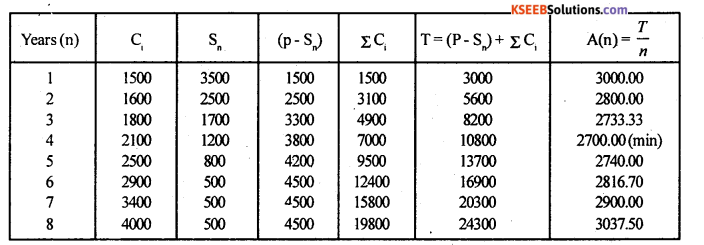
Here the average annual cost A(n) is minimum for n = 4
∴ The optimal replacement age is n = 4 years i.e. the machine should replace (after running) for 4th year.
Question 36.
Given n = 4 and R. : 14, 8, 11, 9, 12, 8. find the control limits and construct R-chart.
Answer:
Here n = 4, k = 6 and standards are not given / known.
\(\bar{R}=\frac{\sum R}{k}=\frac{62}{6}=10.33\)
The control limits for R-chart are
C.L = R̄ = 10.33
L.C.L = D3R̄ = 0 × 10.00 = 0
U.C.L = D4R̄ = 2.282 × 10.33 = 23.37
The R chart is
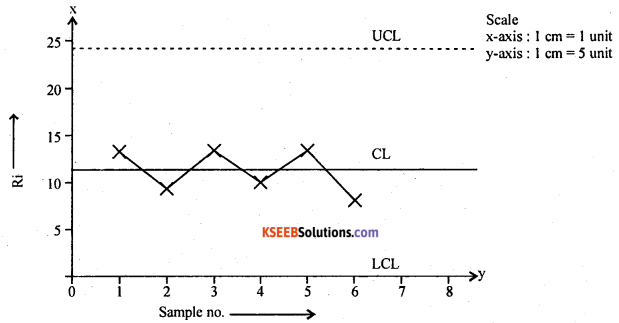
Interpretation: All points are within control limits, the process in control.
Section – D
I. Answer any TWO of the following questions: ( 2 × 10 = 20 )
Question 37.
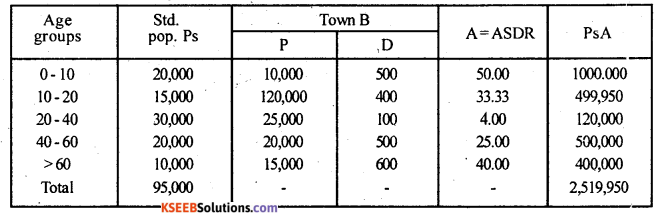
(a) Calculate St.D.R. (B) taking town A’s population as standard.
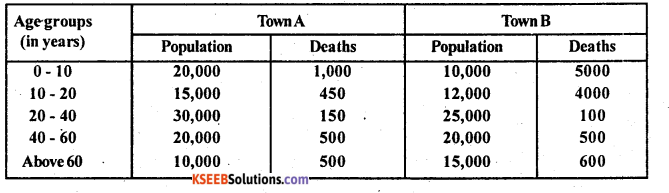
Answer:
Since Town A’s population is taken as standard so compute SDR(B) = \(\frac{\sum_{s} P_{s}}{\sum P_{s}}\)
B =ADDR’s of B ; Ps=standard popn. of A

(b) Calculate CBR, GSR and ASFR (30 – 40) from the following data:
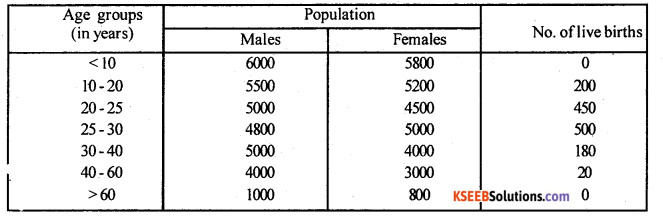
Answer:


(Note: In the above questions class intervals are not in order)
Question 38.
Construct Dorbish-Bowley and Marshall-Edgeworth’s Quantity index numbers. Comment on the result.
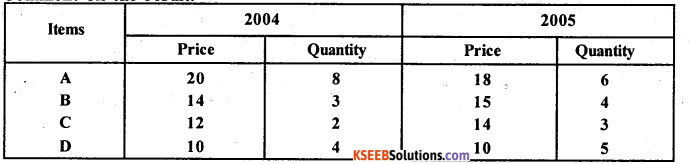
Answer:
Dorbish-Bowley Quantity Index number is
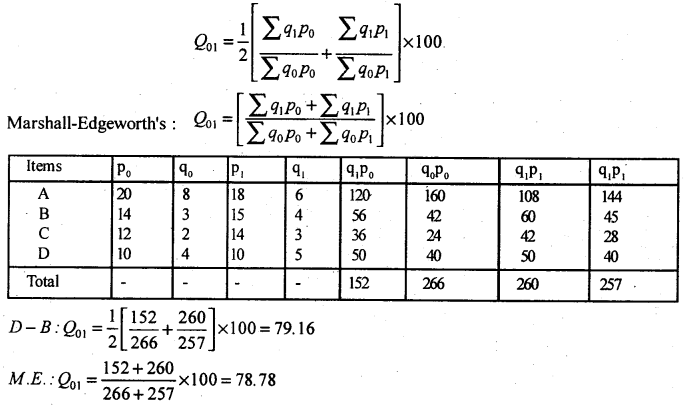
The quantity level in the year 2005 is 79% of the quantity level in the year 2004.
![]()
Question 39.
Monthly income of employees follows Normal distribution with mean Rs. 4,000 and S.D. Rs. 100. Find the probability that a randomly selected employee has income,
(a) > Rs. 3800 (b) > Rs. 4150.
Answer:
Let x be the monthly income is a Normal variate with mean µ = 4000 and σ = 100 then S.N.V is
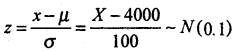
(a)
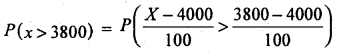
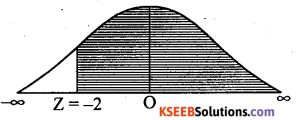
= P (z > -2)
= Area from (-2) to ∞ = 0.9772
OR = Area from 0 to (-2) + Area from 0 to ∞
= 0.4772 + 0.5 = 0.9772
(b)
![]()
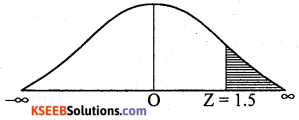
= P (z > 1.5)
= Area from 1.5 to ∞ = 0.0668
OR = Area from 0 to ∞ – Area from 0 to (1.5)
= 0.5-0.4342 = 0.0658
Question 40.
(a) Test at 1% level of significance whether there is any significant difference between observed and expected frequencies.

H0 : There is no significant difference between observed and expected frequencies.
H1 : There is a significant difference between observed and expected frequencies. (Right tail test )
The test statistic is:-
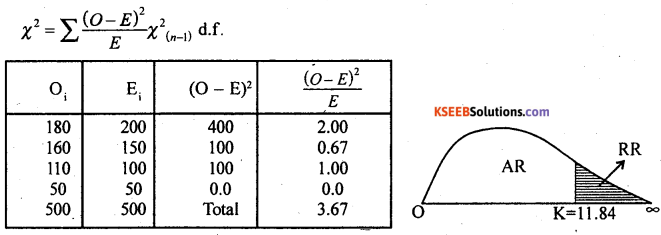
χ2cal = 3.67
At α = 1 % the upper tail critical value for (n – 1) = (4 – 1 )= 3 d.f., k = 11.34
Here χ2cal > k
∴ H0 is accepted.
Conclusion: There is no significant difference between observed and expected frequencies.
(b) The following data gives time taken to travel from Bangalore to Mysore on 6 random days. Test at 5% the hypothesis that the mean travel time is 160 minutes.

Answer:
Given n = 6 , α = 5% , μ = 160
H0 : Mean travel time is 160 min (i.e. H0 : μ= 160)
H1 : mean travel time differs from 160 min (H1 : μ ≠ 160) (Two Tail test)
The test statistic is:-
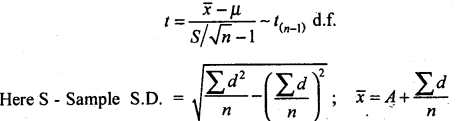
Let x be the time in min.

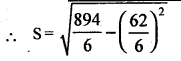
s = 6.5
X̄ = 150 + \(\frac{62}{6}\)
X̄ = 0.1135
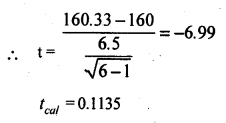
tcal = 0.1135
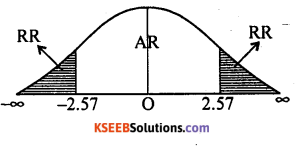
At α =5% for (n – 1) = (6 – 1) = 5 d.f. the two Tail critical values are
-k1 =-257 and k2= 2.57
Here tcal < -k1 / tcal is in rejection region
∴ H0 is rejected and H1 is accepted.
Conclusion: Mean travel time differs from 160 min.
Section – E
V. Answer any TWO of the following questions: ( 2 × 5 = 10 )
Question 41.
For a Hypergeometric distribution, the parameters are a = 7, b = 5, and n = 8. What is the range? Find the S.D.
Answer:
For a hypergeometric distribution:
Range = min (a, n)
= min (7, 8)
Range =0,1,2,3,4, 5, 6, 7.
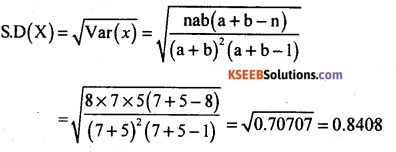
![]()
Question 42.
Fit a Poisson distribution and obtain the theoretical frequencies :

Answer:
If X is a poisson variate the parameter λ is obtained as :
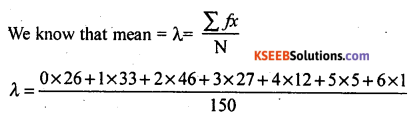
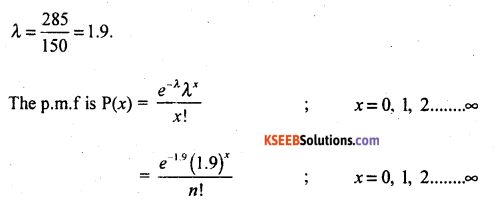
Theoretical frequency : Tx = P(X)N.
T0 = P(x = 0) × 150
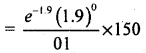
T0 = 0.1496 × 150 = 22.44

T6 or more = N – [T0 + T1 + T2 + T3 + T4 + T5] .
= 150 – [22.44 + 42.64 + 40.50 + 25.65 + 12.18 + 4.63]
T0 or more = 150- 148.01 = 1.99.
The distribution of observed and theoretical frequency is : (Approximated)

Question 43.
On an average a box contains 2 defective items. Find the probability that a randomly selected box has
(a) 3 defective items (b) at the most 2 defective items
Answer:
Let X be the average number of defective items is a Poisson variate with the parameter λ = 2
The p.m.f. is :

Question 44.
A company has to supply 12000 units of a product per year to its customers. The shortage cost is assumed to be infinite. The holding cost is Rs. 0.2 per unit per month and set up cost is Rs. 350. Determine
(a) Number of orders per year.
(b) Minimum total variable cost per month.
Answer:
R = 12,000; C1 = Rs. 0.2 per unit per month
= Rs.0.2 × 12 = 2.4 per year
C3 = Rs. 350 (shortage cost is not given use EOQ model I)
(a) Number of orders per year: \(n^{0}=\frac{1}{t^{0}}\)

(b) Minimum total variable cost per month
