You can Download Chapter 1 Vital Statistics Questions and Answers, Notes, 2nd PUC Statistics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Statistics Question Bank Chapter 1 Vital Statistics
2nd PUC Statistics Vital Statistics One and Two Marks Questions and Answers
Question 1.
Define vital statistics.
Answer:
Vital statistics is the science, which deals with the analysis and interpretation of numerical facts regarding vital events occurring in a human population
Question 2.
What are vital events?
Answer:
Vital events are the events, which are occurring, in human life such as births, deaths, sickness, marriages, divorce, migration etc.
Question 3.
Mention any two uses of Vital Statistics.
Answer:
Vital Statistics is used,
- to study the Demographic structure & trend in the population
- use in public administration. OR
- use to operating agencies
- to researchers
Question 4.
What are the sources of vital statistics?
Answer:
Registration method and Census method
Question 5.
Define C.B.R, G.F.R, A.S.F.R, C.D.R, A.S.D.R, S.D.R, M.M.R, I.M.R, N.M.R, G.R.R, and N.R.R.
Answer:
CBR is defined as the average number of live births occurring in a population of 1000 in a year.
- GFR is defined as the average number of live births occurring to 1000 women of childbearingage in a year;
- ASFR is defined as the average number of live births occurring to 1000 women of specified age in a year.
- CDR is the average number of deaths occurring in the year per 1000 population.
- ASDR is the average number of deaths occurring in the year in the specified age group.
- SDR is defined as the weighted average of ASDR’s with respect to standard population
ie SDR = \(\frac{\Sigma \mathrm{PA}}{\Sigma \mathrm{P}}\) - IMR is defined as the average number of deaths of Infants in a year per 1000 infant population.
- MMR is defined as the ‘the number of deaths of mothers due child birth occurring in a region’ in the year per 100,000 live births.
- NMR: Neo-natal mortality rate is defined as ‘the average number of neo-natal deaths 1000 live births in a year’.
- The gross reproduction rate (GRR) is the average number of daughters that would be born to a woman (or a group of women) if she survived at least to the age of 45 and conformed to the age-specific fertility rate of a given year.
- Neo-natal mortality rate is defined as ‘the average number of neo-natal deaths 1000 live births in a year’.
OR Write the formula of all the above.
![]()
Question 6.
What is Death Rate/Mortality Rate?
Answer:
It is the number of deaths occurring in the population OR It is the rate of decrease of population due deaths occurring in the population per 1000 population in the year.
Question 7.
What is a Life table?
Answer:
Life table is a tabular presentation of numerical data describing the mortality experience of a cohort.
Question 8.
What is cohort?
Answer:
Cohort is a group of individuals who born at the same and experiences the same mortality conditions
Question 9.
What is Radix?
Answer:
Radix is the size of the cohort, and usually is 100,000 individuals
Question 10.
What is the Life expectancy/Expectation of life?
Answer:
It is the expected number of years of life that a person of age ‘x’ can live there after.
Question 11.
Mention any one use of Life table.
Answer:
They are used in computation of actuarial of premium, bonus etc, of policies by Insurance Agencies. OR
- Life Tables are used in research activities in Biology, Medicine, Pharmacology, Demography, Psychology, Sociology etc.
- They are used to study population growth and forecast the size and sex distribution of the
Population. OR - Life Tables give Mortality and Survival ratios at different ages.
- Life tables give the life expectancy at different age. OR
- These are useful in public administration, heath care, planning and population control
![]()
Question 12.
Define Total fertility rate.
Answer:
If ASFR is calculated for the age group of 5 years, then,
TFR = 5 ΣQuinqennial ASFR
Question 13.
What are Quinquennial A.S.F.R’s?
Answer:
If the A.S.F.R’s calculated with a width of 5 years are called Quinquennial ASFR’s.
Question 14.
Given E Quinqennial ASFR = 400, find TFR.
Answer:
TFR = 5 ΣQuinqennial ASFR = 5 x 400 = 2000 . .
Question 15.
Explain briefly Registration method.
Answer:
Registration method is the method of continuous, permanent and compulsory recording of vital events due to the legal importance occurring in the population as and when they happen. Vital statistics are obtained from the records of Zilla panchayath offices, Taluk panchayath offices, Hospitals etc, when births are registered the information regarding sex of a baby, age and religion of a mother, father are recorded.
Question 16.
Explain briefly the census method.
Answer:
Census method is the method of complete enumeration of each and every unit of the population of the particular area under study, in India Decennial census [once in every ten years]are conducted, at the census, including all the vital events, an exhaustive information regarding economic and social status of the population are also collected.
Question 17.
State any two differences between
(a) C.D.R & S.D.R.
(b) C.B.R. & G.F.R (Give any two comparisons between CDR AND STDR)
Answer:
(a) CDR is a approximate measure of mortality-SDR is used for comparison of mortality
CDR does not consider the age composition of the population- SDR consider the age composition of the Population.
Differences between CDR and SDR:
| SL.No | CDR | SDR |
| 1. | It does not require age composition | It require age composition |
| 2. | It cannot be used for comparison of mortality of different localities | It be used for comparison of mortality of different localities |
| 3. | It needs no. of deaths and | It needs deaths, population and population standard population |
(b) CBR indicates the growth of population of due to births-GFR does not indicate the growth of population due to births, because it is based on only a part of the population CBR considers the population as a whole-GFR considers only women population of childbearing age.
![]()
Question 18.
Define Maternal Mortality Rate
Answer:
MMR is defined as the ‘the number of deaths of mothers due child birth occurring in a region’ for every 100,000 births occurring in the year.
Question 19.
Which measure is used for comparing the ‘health conditions’ of two towns?
Answer:
SDR’s
Question 20.
In a year, the CDR for a population of 3 lakhs is 8. Find the number of deaths.
Number of deaths occurring in the year
Ans

Question 21.
What is Birth Rate/Fertility Rate?
Answer:
It is the number of live births occurring to women of child bearing age OR It is rate of increase of population due births occurring to women of child bearing age per 1000 population in the year
Question 22.
What is Longevity in Life table?
Answer:
Longevity is the expected number of years that a newborn baby would live. OR “Life expectancy, of a new born baby is called Longevity”
Question 23.
Write down the components of a Life table
Answer:
Components of Life table is:-

Question 24.
In a community, in a specific year, 3250 live births occurred. In the case of 35 of the above, the mother died due to childbirth. Compute M.M.R.[per 1000]
Answer:

![]()
Question 25.
In a community, in a specific year, 4000 live births occurred. In the case of 50 of the above, the mother died due to child birth. Compute M.M.R.[per 1000].
Answer:

Question 26.
The Quinquennial ASFRs for women of childbearing age of a community are 26 63, 65, 46, 24, 13, and 7. Compute TFR.
Answer:
T.F.R = ΣQuinquennial ASFRs = 5 [26 + 63 + 65 + 46 + 24 + 13 + 7] = 1220
Question 27.
Calculate Maternal Mortality Rate [per 1000] from the following data.
Answer:
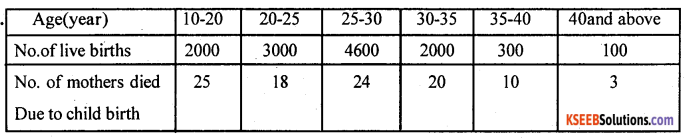

Question 28.
In a year, the average population of town was 1, 50,000. The number of live births occurred in that year in the town was 6,000.Find Crude Birth Rate
Answer:
Write CBR formula; CBR = \(\frac{6000}{150000}\) x 1000 = 40
Question 29.
Find Pt given Po = 1,26,305; Births = 24,500; Deaths = 4,050; Immigrants = 8,065 and Emigrants=6000.
Answer:
Pt = P0 + (B – D) + (I – E); = 1,48,820.
![]()
Question 30.
In a year, in a community there were 6500 live births. The number of infants died in the year was 350, of the infants deaths in 18 cases the new born babies died within one month. Find IMR and NMR.
Answer:

Question 31.
The quinquennial age specific fertility rates for women of child bearing age group of a community are 25, 60, 70, 40, 20, 12 and 5. Compute TFR.
Answer:
TFR = 5 ΣQuinquennial ASFRs = 5 x [25 + 60 + 70 + 40 + 20 + 12 + 5]
= 5 x 232 = 1160.
Question 32.
What is death rate?
Answer:
It is the number of deaths occuring in the population in the given region of 1000 population.
Question 33.
Mention any two measures of Mortality.
Answer:
Crude Death rate, Age specific death rate.
Question 34.
Mention any two measure sof Fertility.
Answer:
Crude Birth rate, General Fertility, etc.
Question 35.
What is Motality ratio?
Answer:
It is the ratio that a randomly selected person aged ‘x’ years does not survive till the age of (x + 1) years denoted by \(\mathrm{q}_{\mathrm{x}}=\frac{\mathrm{d}_{\mathrm{x}}}{l_{\mathrm{x}}}\)
Question 36.
What is survival ratio?
Answer:
It is the ratio that a randomly selected person aged ‘x’ can survive till that age (x + 1) year denoted by Px = 1= qx.
Question 37.
What do you mean by Quinquennial ASFR’s?
Answer:
If ASFR’s calculated for the age group of 5 years. It is called Quinquennial ASFR’s.
![]()
Question 38.
Write any two differences of CBR and ASFR.
Answer:
- CBR is the average number of live birth occuring in the year per 1000 population.
- ASFR is the average number of live births occuring in the specified age group in the year per 1000 women in the specific age group.
- CBR, does not include the age and sex composition of the population.
- ASFR it includes the age and sex composition of the population.
Question 39.
Mention any two differences of CDR and ASDR.
Answer:
- CDR is the number of deaths occuring in the year per 1000 population.
- ASDR in the number of deaths occuring in the specific age group in the year per 1000 population of the specific age group.
- CDR does not consider the age composition of the population.
- ASDR takes into consideration of the age composition of the population.
Question 40.
Explain briefly Registration method.
Answer:
Registration method is the method of continous, permanent and compulsory recording of vital events due to the legal importance.
Question 41.
Explain briefly census method?
Answer:
Census method is the complete enumeration of each and every unit of the population of the particular area under study.
![]()
Question 42.
What is total fertility rate?
Answer:
It is the sum of annual ASFR’s for all age groups (15 – 49) years,
i.e., TFR = Σ annual ASFR’s.
If it is calculated for the age groups of 5 years called quinquennial ASFR’s.
Then, TFR = 5 Σ Quinquennial ASFR’s.
Question 43.
Give the formula for calculating Infant mortality rate.
Answer:
Infant mortality rate (I.M.R)

Question 44.
Give the formula for calculating matenal mortality rate.
Answer:

Question 45.
What is standardised death rate?
Answer:
Standardised death rate is the weighted Arithmatic mean of deaths in the different age groups and the standard population in the age group
i.e; SDR = \(\frac{\Sigma \mathrm{PA}}{\Sigma \mathrm{P}}\)
where P – Standard Population ; A – ASDR’s
Question 46.
Give the formula obtaining the population in between two census.
Answer:
Pt = Po (B – D) + (I – E) ; where Pt = Population after time ‘t’ after census year.
P0 = Population in the census year.
B, D, I and E – Births, deaths, immigrations and emigrants in the time period.
Question 47.
Calculate ASFR’s for the age groups (10 – 20) and (20 – 40) years.

Answer:
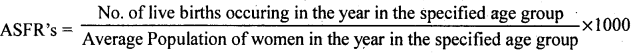
ASFR = (10 – 20) = \(\frac{410}{15000}\) x 1000 = 27.3
ASFR = (20 – 40) = \(\frac{650}{22000}\) x 1000 =29.55
Question 48.
Compute general fertility rate from the data given below:

Answer:
General Fertility rate;

Question 49.
Calculate ASDR’s for the age groups (0-5) and (40-60) years from the following data.

Answer:
![]()
ASFR = (0 – 5) years = \(\frac{410}{22000}\) x 1000 = 18.63
ASFR = (40 – 60) = \(\frac{150}{8000}\) x 1000 = 18.75
Question 60.
If TFR of a certain locality is 2750 then find the average number of children born to Women.
Answer:
Average number of children bom to Women = \(\frac{TFR}{1000}\) = \(\frac{2750}{1000}\) 2.75 = 3 (Approx)
![]()
Question 61.
The certain town, in a year 25000 births have occured. The number of infant deaths in the year was 1350. Among the live births in 150 cases, mother died due to child birth problems. Calculate infant motality rate and maternal mortality rate.
Answer:
The imfant mortality rate:

Question 62.
In a town, in a year 2200 live births occurred and of these 430 died in the same year. Find IMR.
Answer:
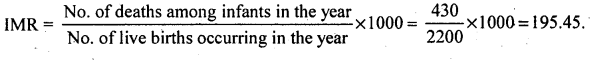
Question 63.
Calculate Infant mortality rate from the following data.

Answer:
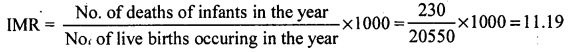
Question 64.
Calculate maternal mortality rate from the following data.

Answer:
The maternal mortality rate is

Question 65.
In a town, 231440 births occured in an year and 7860 infants died in the same year. Find I.M.R.
Answer:
Infant Mortality Rate is:
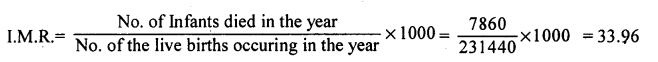
Question 66.
In an year, in a community there were 12750 live births occurred. 103 of these babies lost their mothers at the time of delivery. Find MMR.
Answer:
The maternal mortality rate is:

![]()
Question 67.
In a given year, the CDR for a population of 1,50,000 is 12. Find the number of deaths.
Answer:
CDR = 12 ; Population = 1,50,000
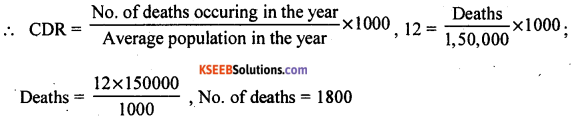
Question 68.
Calculate metarnal mortality rate (per 1000) from the following data.

Answer:
Maternal Mortality Rate (M.M.R) is

Question 69.
In a year the C.D.R. for a population of 3 lakhs is 8. Find the number of deaths.
Answer:
Crude Death Rate (C.D.R.)

Question 70.
In a community, in a specific year, 3250 live births occurred. In the case of 35 of the above, the mother died due to childbirth. Compute M.M.R. (per 1000).
Answer:
Maternal Mortality Rate –

M.M.R = 10.769.
Question 71.
In a particular city out of 1800 live births in a year, 90 newborn babies died within 28 days. Calculate neonatal mortality rate.
Answer:
Neo-natal mortality rate:
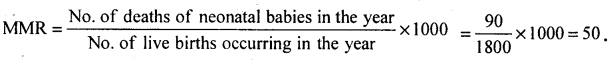
![]()
Question 72.
In a town, in a year 3120 live births occurred and of these 160 infants died in the same year. Of all the newborn babies in 15 cases died within one month. Compute I.M.R and N.M.R.
Answer:


2nd PUC Statistics Vital Statistics Five Marks Questions and Answers
Question 1.
Explain Registration method and Census method of collecting Vital Statistics.
Answer:
Registration method is the method of continuous, permanent and compulsory recording of vital events due to the Legal importance. When ever Vital events Occur in the population, are registered at the Registers of municipal offices, panchayat offices, Hospitals etc. When births are registered information of age of mother, caste, sex of a baby etc., are registered. Similarly when death occurred, information regarding sex , religion, marital status, age of death, cause of death etc., are registered.
Census method is the complete enumeration of each and every unit of the population of a particular area under study, at regular intervals. In India, once in every 10 years census is conducted. In this method information regarding birth, death, marriage, literacy etc., are collected.
Question 2.
In a year in a population of 1,00,000, there were 18S0 live births and 1680 deaths. Assuming the population is closed for migration. Calculate CBR and CDR.
Answer:
P0 = 1,00,000, B= 1850, D= 1680
Pt = Population at the end of the year = P0 + (B – D)
= 1,00,000+ (1850 – 1680) = 1,00,170

![]()
Question 3.
The following data gives the age distribution and number of deaths in a population. Find ASDR’s.

Answer:
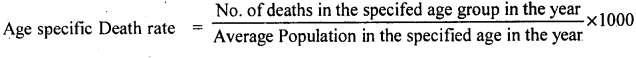
ASDR. (Below 10 years) = \(\frac{215}{21000}\) x 1000 = 10.24
ASDR (10-20) years = \(\frac{150}{16000}\) x 1000 = 9.375
ASDR (20-30) = \(\frac{75}{15000}\) x 1000 = 5
ASDR (30-40) = \(\frac{15}{12500}\) x 1000 = 1.2
ASDR(40-50) = \(\frac{22}{4000}\) x 1000 =5.5
ASDR (50 and above) =\(\frac{38}{1300}\) x 1000 = 29.23
Question 4.
Calculate crude death rate and standardised death rate from the following data:
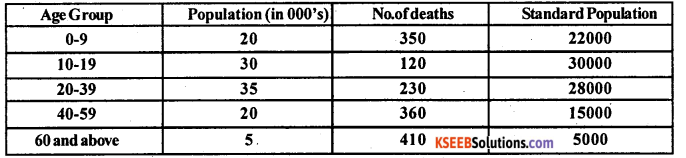
Answer:
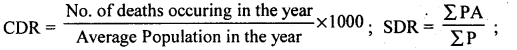
P – standard population; A ASDR’s
CDR = \(\frac{1470}{110000}\) x 1000 = 13.36
SDR = \(\frac{1368960}{100000}\) = 13.68
Question 5.
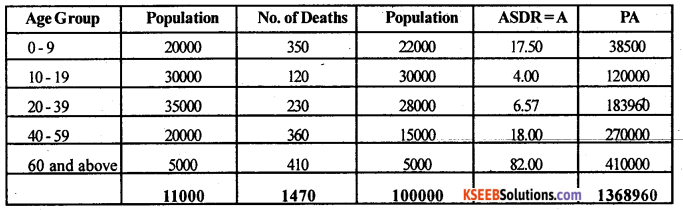
The following table gives the age and sex composition of population along with the number of live births in an year. Calculate total fertility rate.
Answer:
TFR = 5 Σ Quinquennial ASFR’s
ASFR
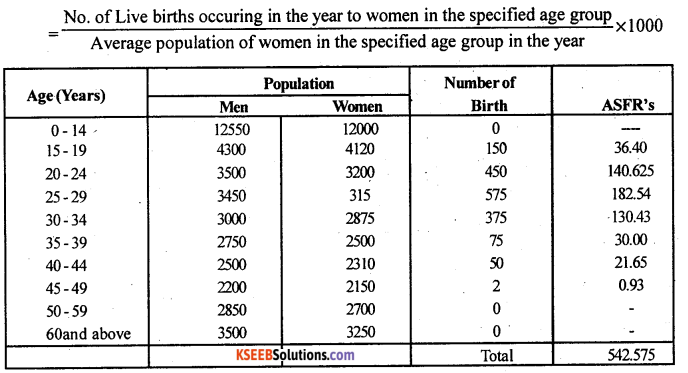
ASFR(15 – 19) = \(\frac{150}{4120}\) x 1000 = 36.40
TFR= 5 x 542.575 = 2712.875 births per 1000 women.
Question 6.
Calculate total fertility rate :
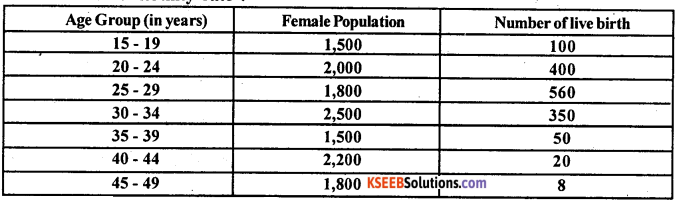
Answer:
Total Fertility Rate = EQuinquennial as ASFR

ASFR(15 – 19) = \(\frac{100}{1500}\) x 1000 = 66.66
TFR= 5 x 764.63 = 3823.15 births per 1000 women.
Question 7.
Write down the components of the life table.
Answer:

Note: For explanation of components of life table Refer, P. No. 13.
![]()
Question 8.
Calculate “Total Fertility Rate” for the following data.

Answer:
The total fertility rate is:
T.F.R. = 5 x Σ Quinquennial ASFR’s
ASFR

T.F.R. = 5 x 474.93 = 2374.65 Births per 1000 women.
Question 9.
Calculate standarlised death rates from the following data.
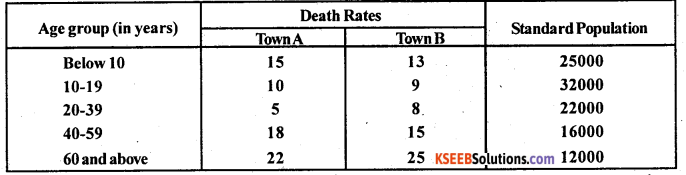
Answer:
Here Death rates means : Age specific death rates of Town A (A) and Town B (B) are given.
So, SDR(A) = \(\frac{\Sigma \mathrm{PA}}{\Sigma \mathrm{P}}\)
SDR(B) \(\frac{\Sigma \mathrm{PB}}{\Sigma \mathrm{P}}\)
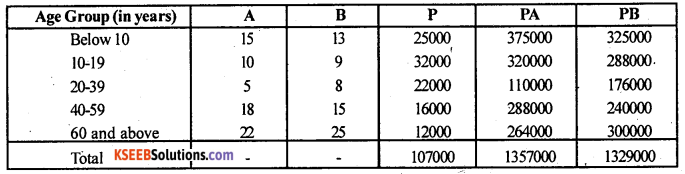
SDR(A) = \(\frac{1357000}}{107000}}\) = 12.68
SDR(B) = \(\frac{1329000}}{107000}}\) = 12.42
![]()
Question 10.
From the following data compute
(i) GF.R.
(ii) A.S.F.R for the age groups (20-29)

Answer:

\(\frac{1878}{36320}\) x 1000
GF.R. =51.7
Here women of child bearing age is (15-49) years only.
A.S.F.R for the age group (20-29) in the year

Question 11.
From the following data. Calculate the Standardized Death Rates for Locality A and Locality B.
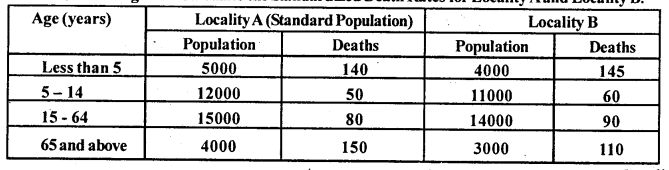
Answer:
Since Locality A population is considered as standard so, compute CDR for LocalityA and for Locality B,SDR.

SDR (B) = \(\frac{489780.00}{36000}\) = 13.605
SDR (B) = \(\frac{\Sigma \mathrm{PB}}{\Sigma \mathrm{P}}\); P = Standard popn. (of B), B = ASDR’S
No.of deaths occurring in the year

CDR(A) = \(\frac{420}{36000}\) x 1000=11.67
For Locality B
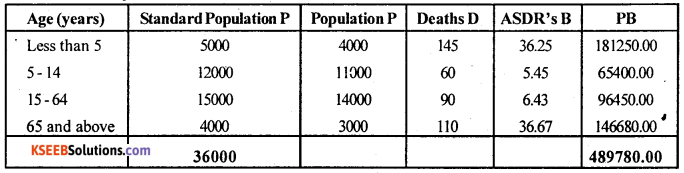
SDR (B) = \(\frac{489780.00}{36000}\) = 13.605
Question 12.
Compute Crude Death Rate and Standardised Death Rate for the following data:
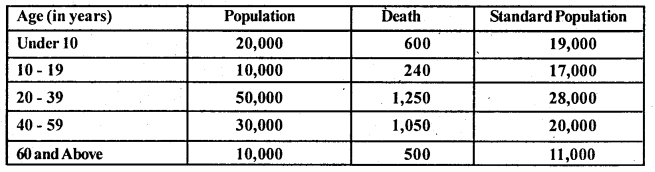
Answer:
Crude death rate (C.D.R)
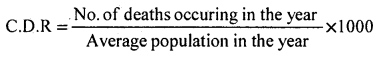
S.D.R = \(\frac{\Sigma \mathrm{PA}}{\Sigma \mathrm{P}}\); Where P – standard population, A – age specific death rate
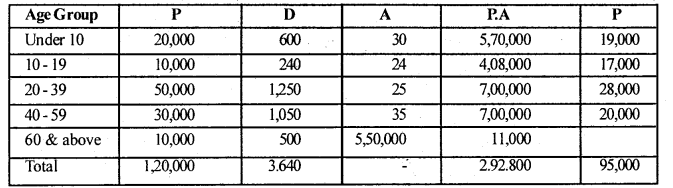
CDR(A) = \(\frac{3640}{120,000}\) x 1000 = 30.33
SDR (B) = \(\frac{2,92,000}{95,000}\) = 30.82
![]()
Question 13.
Calculate gross reproduction rate from the following data and comment on population status.
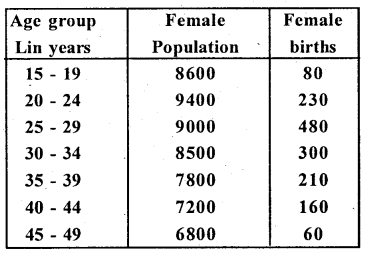
Answer:
Gross reproduction rate:
G.R.R = (i) \(\sum_{i=15}^{49} \)W.S.F.R
Where i – Age width
W.S.F.R = \(\frac{\text { Female births }}{\text { Female population }} \) x 1000
W.S.F.R( 15-19) = \( =\frac{80}{8600}\) x 1000 = 9.38
Similarly calculate for other age groups.

ΣY W.S.F.R = 180.43; i = Age width = 5
∴ G.R.R = 5 x 180.43 = 902.15 Female births per 1000 women of child bearing age.
No. of Female children born per women = \(\frac{\mathrm{G} \cdot \mathrm{R} \cdot \mathrm{R}}{1000}\)
= \(\frac{902.15}{1000}\) = 0.902
Sience this rate. / value is below one, the papulation decreases.
Question 14.
Calculate net reproduction rate from the data given below and comment on population status.

Answer:
Nety Production:
N.R.R = (i) \(\sum_{i=15}^{49} \) W.S.F.R x S
Where i – age width, S-Survival Rates.
W.S.F.R = \(\frac{\text { Femalebirths }}{\text { Female population }}\) x 1000
W.S.F.R X S(15 – 19) = 25 x 0.96 = 24
Similarly calculate for other age groups

Σ W.S.F.R x S = 596.62
∴ M.R.R = 5 x 596.62 = 2983.09 Female births occur per 1000 women of (15 = 49) years.
N.R.R. per women = \(\frac{\mathrm{N} \cdot \mathrm{R} \cdot \mathrm{R}}{1000}=\frac{2983.09}{1000}= 2.983 \) Female Children bom per women.
Here the N.R.R. per women is more than one.
Therefore, the population increases. [Because the mother will be replaced by daughters so that fertility will be continued].
2nd PUC Statistics Vital Statistics Ten Marks Questions and Answers
Question 1.
From the following data, calculate Total Fertility Rates and compare the fertility of the two cities:
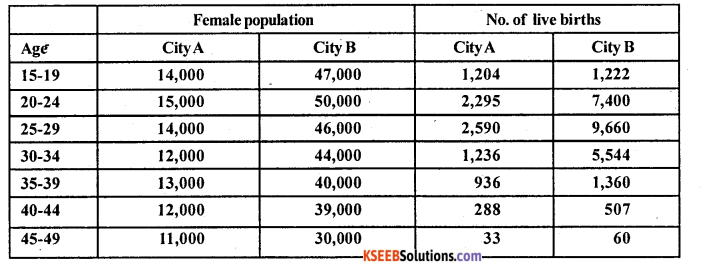
Answer:
Total Fertility Rate = 5ΣQuinquennial ASFR’s

ASFR(15-19) = \(\frac{1204}{14000}\) x 1000 = 86.
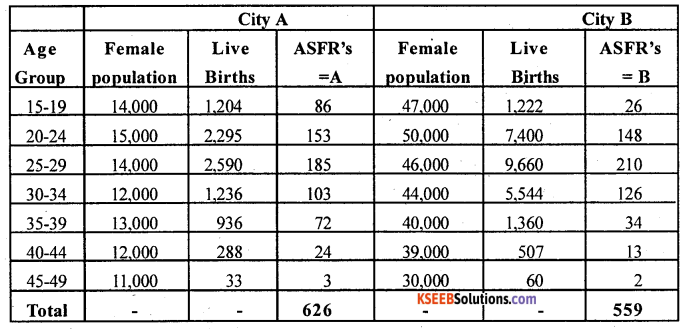
T.F.R (A) = 5 x 626 = 3130
T.F.R.(B) = 5 x 559 = 2795
Here TFR (A) > TFR (B)
∴ City A is more fertile than City B
Question 2.
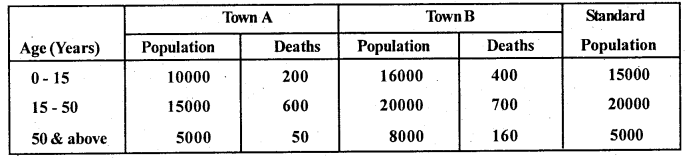
Compute Standardised death rates for the two towns and give your comments.
Answer:
SDR (A) =\(\frac{\Sigma \mathrm{PA}}{\Sigma \mathrm{P}}\) ; SDR(B) =\(\frac{\Sigma \mathrm{PB}}{\Sigma \mathrm{P}}\)
A = ASDR’s of Town A, B = ASDR’s of Town B, P = Std Population.
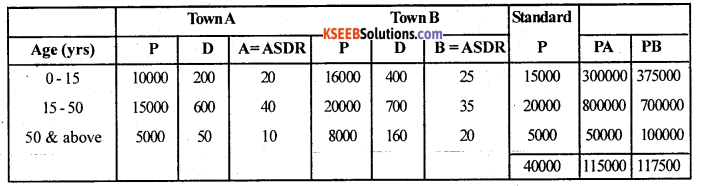
SDR (A) = \(\frac{1150000}{40000}\) = 28. 75 ;
SDR (B) = \(\frac{1175000}{40000}\) = 29.375
Death rate of Town B is more than Town A. Town A is more healthier than town B.
![]()
Question 3.
From the following data, Calculate the standardised death rate for the two populations A and B
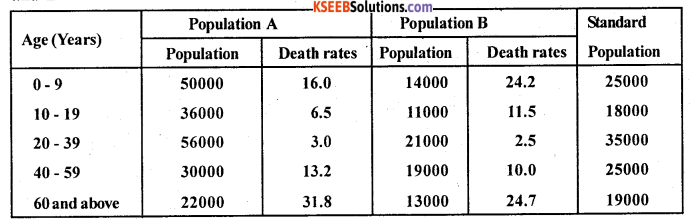
Answer:
Here Death rates are given, i.e., ASDR’s of Population A and B. Let A and B be ASDR’s (Death rates) of Population A and B.
SDR (A) = \(\frac{\Sigma \mathrm{PA}}{\Sigma \mathrm{P}}\) ; SDR(B) = \(\frac{\Sigma \mathrm{PB}}{\Sigma \mathrm{P}}\) Where P = Std. Population.
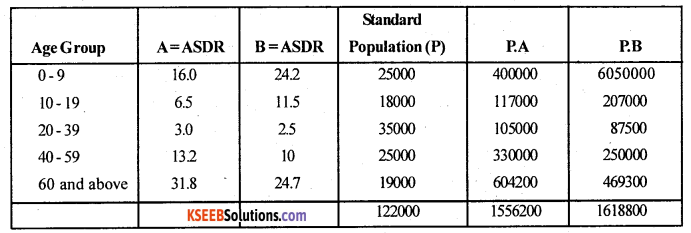
SDR (A) = \(\frac{1556200}{122000}\) = 28. 75 ;= 12.756;
SDR (B) = 13.269.
Question 4.
Compute the standardised death rates for the following two populations A and B by taking the population A as the standard.
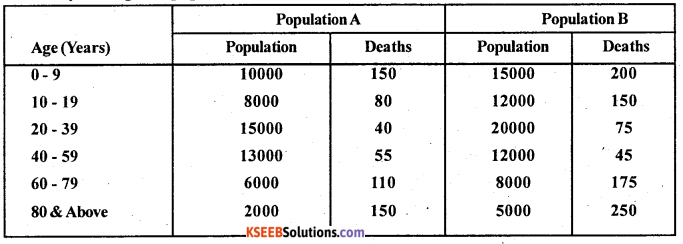
Answer:
Since Population A is considered as standard Population. So, compute CDR for population A and SDR for Population B.
SDR (A) = CDR(A) = \(\frac{\text { No. of deaths occuring in the year }}{\text { Average Population in the year }}\) x 1000
SDR (B) = \(\frac{\Sigma \mathrm{PB}}{\Sigma \mathrm{P}}\) , B ASDR’s of Population B, P = Standard Population of A.
For Population A :
CDR(A) = \(\frac{585}{54000}\) = 10.83
For Population B
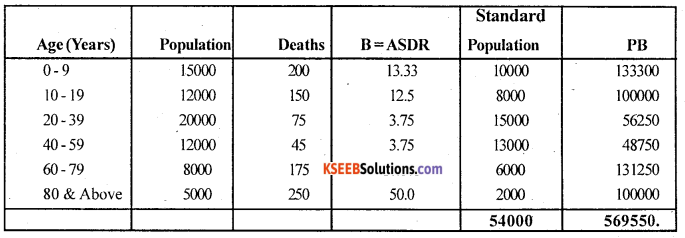
SDR (A) = \(\frac{569550}{54000}\) = 10.547
![]()
Question 5.
From the following data. Calculate standardised death rate for locality A and Locality
B. Which locality is more healthy?
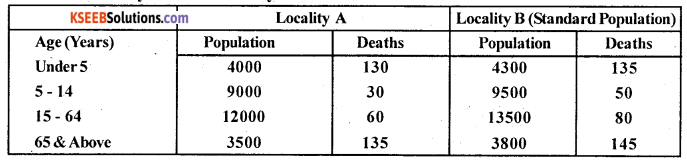
Answer:
Since Population B is considered as standard Population computing CDR is same as the SDR for Population B. .
SDR (B) = CDR(B) = \(\frac{\text { No. of deaths occuring in the year }}{\text { Average Population in the year }}\) x 1000
SDR (A) = \(\frac{\Sigma \mathrm{PB}}{\Sigma \mathrm{P}}\) , B ASDR’s of Population B, P = Standard Population of A.
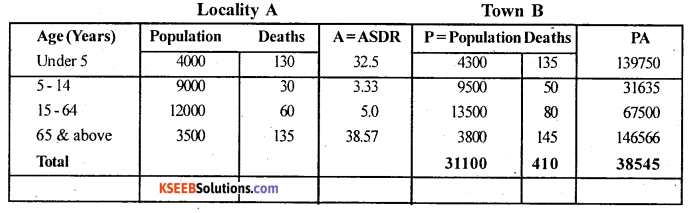
SDR (A) = \(\frac{38545}{31100}\) = 3939
CDR (B) = \(\frac{410}{31100}\) x 1000 = 13.18
Since SDR of A is less in Locality A, it is more healthy.
Question 6.
Calculate standardized death rates from the following data.
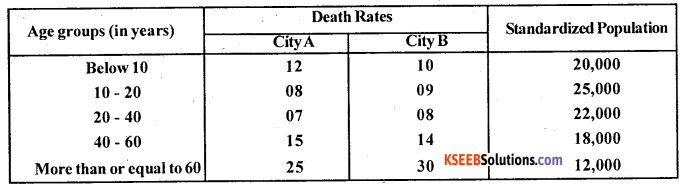
Answer:
Death Rates i.e, ASDR’s for city A and B are given:
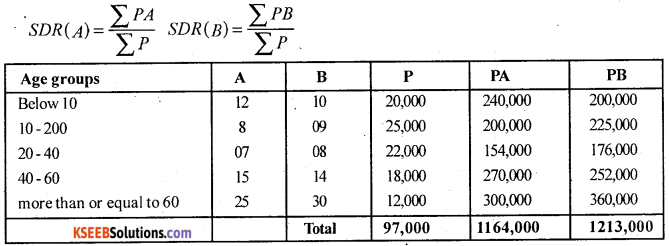
SDR (A) = \(\frac{1164000}{97000}\) = 12
SDR (B) = \(\frac{1213000}{97000}\) = 12.505
Question 7.
For the following data calculate standardized death rates. Hence find which locality is more healthier.
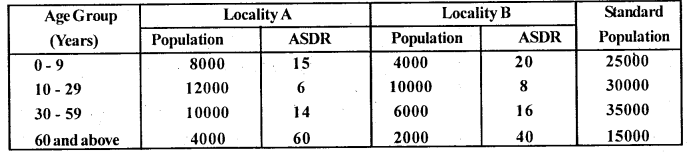
Answer:
Let A and B be the ASDR of locality A and Locality B P – the standard population
Then, SDR(A) = \(\frac{\Sigma \mathrm{PA}}{\Sigma \mathrm{P}}\)
SDR (B) = \(\frac{\Sigma \mathrm{PB}}{\Sigma \mathrm{P}}\)
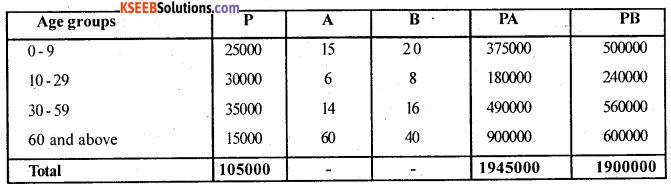
SDR (A) = \(\frac{1945000}{105000}\) = 18.5238
SDR (B) = \(\frac{1900000}{1050000}\) = 18.095
Here, SDR(B) < SDR (A)
Locality B is healthier.
![]()
Question 8.
From the following table calculate standardised death rates and hence tell which town is healthier (take town B as standard)
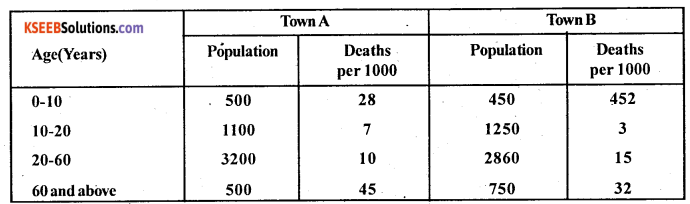
Answer:
Here, Deaths per 1000 population, ie., Age specific death rates of Town A (A) and Town B (B) are given.
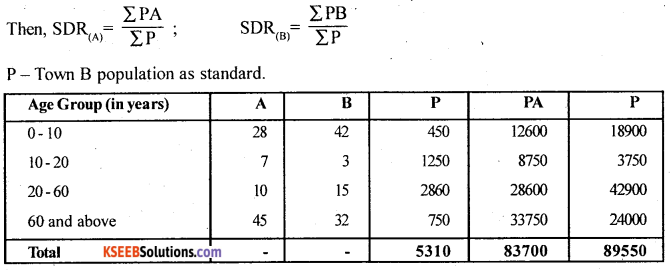
∴ Standardised death rate of Town A is –
SDR (A) = \(\frac{83700}{5310}\) = 15.76
Standardised death rate of Town B is –
SDR (B) = \(\frac{89550}{5310}\) = 16.86
Here SDR(A) < SDR(B).
.’. Town A is more healthier than Town B.
Question 9.
The Population of a city at the end of 2004 was 4,43,850. There were 10,452 births and 6,845 deaths in 2005. The number of emigrants was 12,435. Estimate the population at the end of 2005. Find crude birth rate and crude death rate.
Answer:
Given P0= Population at the end of 2004 = 4,43,850.
B= 10,452, D = 6,845, 1 = 44,680, E= 12,435
The estimate of the population at the end of 2005 is – .
Pt= P0+ (B – D) + (I – E)
= 4,43,850 + (10,452 – 6,845) + (44,680 – 12,435)
= 4,79,702
![]()
The crude birth rate is –
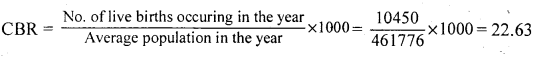
The crude death rate is –
![]()
![]()