You can Download Chapter 3 Time Series Questions and Answers, Notes, 2nd PUC Statistics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Statistics Question Bank Chapter 3 Time Series
2nd PUC Statistics Time Series One and Two Marks Questions and Answers
Question 1.
Define time series/what is time-series? Give an example
Answer:
- A set of figures relating to a variable according to a time is called Time series OR chronological arrangements of the statistical data is called Time series
- Production of a firm arranged from the year 2000 to 2008, Sales statistics of a certain article for the year 1998 to 2005.
Question 2.
What do you meant by trend?
Answer:
Trend is the overall change taking place in the series of the data over a given period.
Question 3.
What do you mean by Secular trend / Seasonal variation / cyclical variation / Irregular variations?
Answer:
- Secular trend/Trend refers to the tendency of the variable to increase, decrease, or remain steady over a given period.
- Seasonal variations refer to the variations caused annually by the seasons of the year. Also includes the variations of any kind which are periodic in nature and whose period is shorter than one year. ( t < 1 year)
- Cyclical variations are fluctuations spread over a period of more than one year. Most of the Time series relating to Economics and Business show some kind of cyclical variations. Cyclical variation is an oscillatory variation, which occurs in four stages, such as (1) Prosperity (2) Decline (3) Depression and (4) Improvement.
- Irregular / Erratic variations are those changes of time series, which are irregular in nature and do not show any pattern. The causes of irregular variations are due to accidental happenings such as wars, earth quacks, floods, famine, fire, strikes, etc.,
Question 4.
Give a difference between ‘cyclical’ and irregular variations in a time series.
Answer:
- Secular trend/Trend refers to the tendency of the variable to increase, decrease, or remain steady over a given period.
- Seasonal variations refer to the variations caused annually by the seasons of the year. Also includes the variations of any kind which are periodic in nature and whose period is shorter than one year. ( t < 1 year)
- Cyclical variations are fluctuations spread over a period of more than one year. Most of the Time series relating to Economics and Business show some kind of cyclical variations. Cyclical variation is an oscillatory variation, which occurs in four stages, such as (1) Prosperity (2) Decline (3) Depression and (4) Improvement.
- Irregular / Erratic variations are those changes of time series, which are irregular in nature and do not show any pattern. The causes of irregular variations are due to accidental happenings such as wars, earth quacks, floods, famine, fire, strikes, etc.,
Question 5.
Give an example for seasonal variation.
Answer:
More sales of woolen clothes in winter season or there is more sales of Ice creams and cool drinks in summer season.
Question 6.
Give an example for upward trend in time series.
Answer:
Prices of petroleum products/Population of India.
![]()
Question 7.
Mention the factors causing seasonal variation
Answer:
Climatic and whether conditions are responsible for the seasonal variation
Question 8.
What are the stages/Phases of a cyclical trend/Business cycle?
Answer:
(1) Prosperity (2) Decline (3) Depression and (4) Improvement.
Question 9.
Which components of time series are applicable in case of
Answer:
- Fire accident in a factory
- Increase of woolen goods during winter
- Fall in the death rate due to advances in Science
- An era of Prosperity
- An increase in employment during harvest season.
– (1) Random, (2) Seasonal, (3) Secular, (4) Cyclical variations (5) Seasonal variation
Question 10.
With which components of a time series would you mainly associated each of the following?
(a) Increase in money in circulation for the last 10 years
(b) Rain fall in Bangalore that occurred for a week in December 2007.
Answer:
(a) Secular trend
(b) Irregular variations
Question 11.
Mention the type of component (T-S) seen in the following :
“Increase in the number of deaths of piligrims due to floods and landslides in the Uttarkhand recently”
Answer:
Irregular variations
Question 12.
What is the name given to the line, which is obtained under method of least squares?
Answer:
Linear/Straight line trend/line
Question 13.
What is a Historigram? /Name the graph of time series.
Answer:
The graph of time series is called Historigram.
Question 14.
Give any two uses of Analysis of Time Series.
Answer:
Analysis of Time series helps to understand the past behavior of the data / to predict the future trend.
Question 15.
What is the duration of seasonal variation?
Answer:
Within one year (t < 1 year)
Question 16.
Mention the conditions to be followed in the method of least squares. /Principles of Method of least squares.
Answer:
The sum of the deviations obtained from the actual and trend values is Zero ie. Σ(Y – Ȳ)=0 and The sum of the squares of the deviations obtained from the actual and trend values is least.
i.e., Σ(Y – Ȳ)2 is least
Question 17.
What do you mean by moving averages?
Answer:
Moving averages are the averages obtained by finding the arithmetic means of successive values of the time series by taking say 3/4/5 years at a time by leaving the first and adding the next; this is to eliminate short-term variations/fluctuations that are present in the time series.
Question 18.
Write any merit and demerit of moving average methods.
Answer:
The merit is it is simple and easy;
Demerit is that, not all trend values can be obtained by this method
![]()
Question 19.
Mention a merit and demerit of least square method
Answer:
It can be used for predicting future trend/Trend values can be obtained for all time points.
Question 20.
Write down the equation for method of least square with the Normal equations.
Answer:
* The equation is y = a + bx; Normal equations are
na + bΣx = Σy;
aΣx + bΣx2 = Σxy
* Quadratic/second degree equation/parabolic trend equation is:
y = a + bx + cx2 : Normal equations are: na + bΣx + cΣx2 = Σy;
aΣx + bΣx2 + cΣ = Σxy ; aΣx2 + bΣx3 + cΣx4 = Σx2y.
Question 21.
Mention any one of use of analysis of time series.
Answer:
Analytical study of the time series will helps to predict / plan for future.
Question 22.
Name the methods of measurement of trend in time series.
Answer:
- Method of moving averages and
- Method of least squares.
Question 23.
What do you mean by secular trend?
Answer:
The term secular trend refer to the tendency of a variable to increase or decrease or to remain constant over a period of time.
Question 24.
Give an example of cyclical variation in a time series.
Answer:
Examples of Business and Economics such as price, sales, production etc.
Question 25.
Write the equation of parabolic trend in measuring the trend.
Answer:
The second degree/parabolic trend/ equation is y = a + bx + cx2
Question 26.
Which component of the time series is associated with deaths due to tsunami?
Answer:
Irregular/random variation.
Question 27.
Which component of Time series is observed in ‘Increase in passengers in train during April and May’?
Answer:
Seasonal Variation.
Question 28.
What is time series? Give an example.
Answer:
Chronological arrangement of statistical data is called time series.
Eg: Arrangement of population of India from 1941-2001

Question 29.
Mention the components of time series.
Answer:
The components of time series are:
- Secular trend.
- Seasonal trend.
- Cyclical trend.
- Irregular / Random Variations.
Question 30.
What do you mean by moving average method?
Answer:
The method of moving average is a simple arithmetic mean calculated successively by taking some specified number of values at a time (m) say 3, 4, or 5 years. The aim of averaging is to remove short term variations in the time series.
Question 31.
What do you mean by method of least squares?
Answer:
In this method a mathematical relation is developed between the time (x) and the values (y). The relation may be used to fit (a) Linear/straight line trend (6) Quadratic trend (c) Exponential trend. Such that “the sum of the squares of the deviations obtained from actual and trend vales is least”.
And these relations are used for computing the trend values in the time series.
Question 32.
Name two methods of measuring secular trend in time series.
Answer:
- Method of moving averages.
- Method of least squares.
![]()
Question 33.
Which component of time series are applicable in case of
(a) Fire accident in a factory
(b) Increase of woollen goods during winter
(c) Fall in the death rate due to advances in science
(d) An era of prosperity.
Answer:
(a) Random / irregular
(b) seasonal,
(c) secular and
(d) cyclical variations.
Question 34.
Let y = a+bx, if a = 25, b = 3.5 findy when x = 4.
Answer:
By substituting a = 25, b = 3.5 and x = 4.
we get y = 15 + 3.5 (4) = 25 + 14 = 39.
Question 35.
In the analysis of time series the fitted Linear trend equation is y = 75.3 – 2.75x estimate trend value when x = 5.
Answer:
By substituting the value of x = 5 in the equation.
We get y = 75.3 – 2.75 (5) = 75.3 – 13.75
∴ y = 61.55.
Question 36.
Which index is used for the measurement of seasonable variation?
Answer:
Seasonal Indices are used for the measurement of seasonal variation.
Question 37.
Which variation is un predrestable and which variation is prediatable?
Answer:
Irregular variations are unprediatable and secular and seasonal variations are predretable.
Question 38.
Diagrammatically represent ‘Business cycle’ with stages.
Answer:
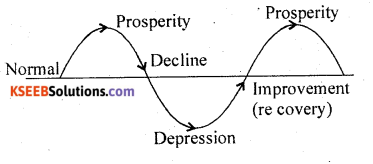
Question 39.
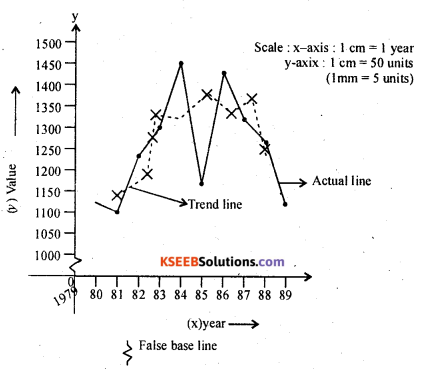
What is graphical / pree – hand method of measurement of trend?
Answer:
In this method the actual values are plotted on a graph and smoth line or curve is drawn.
Again a line or curve is drawn a long the actual line which covers majority of the points according to personal judgment. This line is called line of best fit, is the trend line.
Question 40.
What is semi-average method of measurement of trend?
Answer:
The original values of time series are divided in to two equal parts (if odd number ignoring the middle value) and averages are calculated both the parts, are called semi averages the two points and extending the line which gives the trend of the time series.
Actual values are plotted on a graph which is a history gram and by plotting the semi-averages on a graph joining the two points and extending the line which gives the trend of the time series.
![]()
2nd PUC Statistics Time Series Five Marks Questions and Answers
Question 1.
Mention and explain the components of time series in brief.
Answer:
The components/variations of time series are :
- Secular trend
- Seasonal trend .
- Cyclical variations
- Irregular/ Random variations.
(1) Secular trend: – ‘The term secular trend/ ‘Trend’ refers to the tendency of the variable to Increase or decrease or to remain steady over a period of time’, e.g. The values of population, prices, sales, literacy etc. are all increasing. As against the death rate, illiteracy, travel by bullock carts is decreasing. The rise or fall may be steep or gradual. But they show increasing trend, if we observe over a sufficiently long period of time.(Here the time ‘t’ > lyear)
(2) Seasonal trend: – The term seasonal variations basically refer to the variations caused annually by the seasons of the year. But also includes the variations of any kind which are periodic in nature and whose period is shorter than one year (Here the time’t’ Ex:-
- Sales of cool drinks, ice creams are more in the summer season
- Sale of stationery will be more in June, July.
- The business commercial Bank may reach a peak around the first week of every month.
- Sales of coconuts are always high on Saturday etc.
Hence a clever Businessman will arrange for the production or to maintain stock accordingly to the needs of the season and will earn maximum profit.
(3) Cyclical Variations:- Cyclical variations are the fluctuations spread over a period of more than one year. (Here time ‘t'< lyear). Most of the Time series relating to Economics and Business show some kind of cyclical variations.
Hence ‘cyclical variation is an oscillatory variation which occurs in four stages, such as (1) Prosperity (2) Decline/Recession (3) Depression and (4) Improvement/Recovery
The business cycle is:-
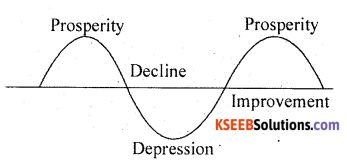
In Prosperity, the curve increases, the business is in boom, the transaction are much more than expected. After reaching the peak of activities the business declines, the curve slopes down. This is called the period of Decline, in Depression the business activities are at the lowest. Then follows a period of improvement in activities and the curve again starts to rise. In this manner the cycle repeats. The interval of time from one prosperity to the other is called the period of cycle. (Here the time ‘t ‘> OR < 1 year) .
(4) Irregular or Random variations: – Irregular variations are those changes of time series which are irregular in nature and do not show any pattern. The causes of irregular variations are due to accidental happenings such as wars, earth quacks, floods, famine, fire, strikes, etc. These factors are unpredictable. Generally such variations last for a short period.
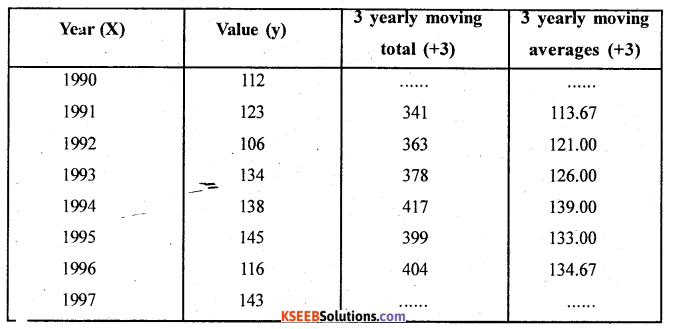
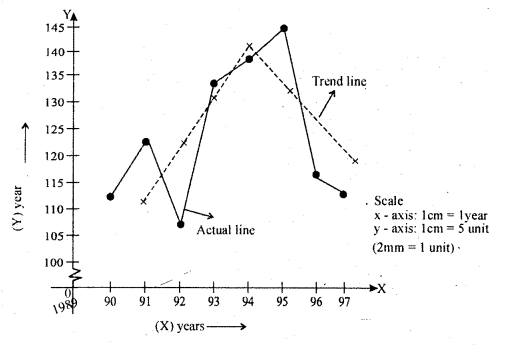
Question 2.
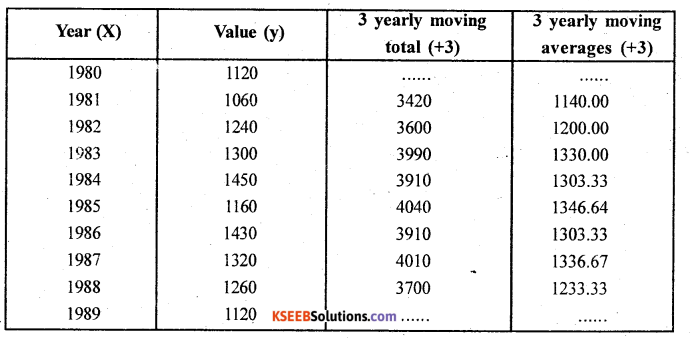
For the following time series calculate the trend by the method of 3 yearly moving averages.

Answer:
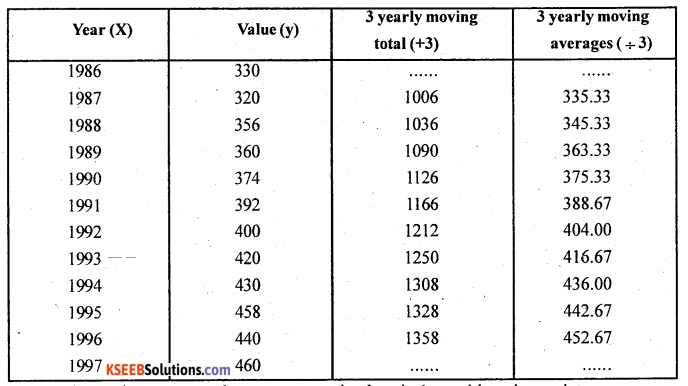
In 3 yearly moving averange there are no trend values in 1st and last time points
Here ŷ – trend values.
![]()
Question 3.
Fit a trend line to the following data by graphical method.

Answer:
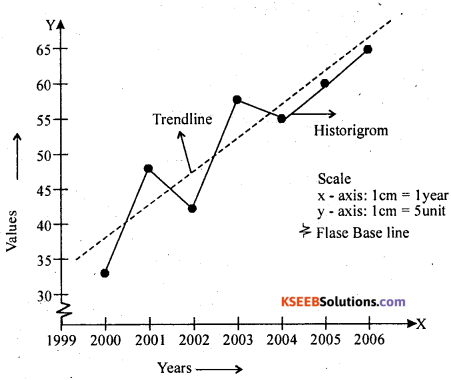
Question 4.
Draw a trend line by thç method of semi-averages for the following time series.

Answer:
Compute averages for the first half and second half values, are the semi-averages
actual and semi-averages on a graph to trend line
Graph of time series.
![]()
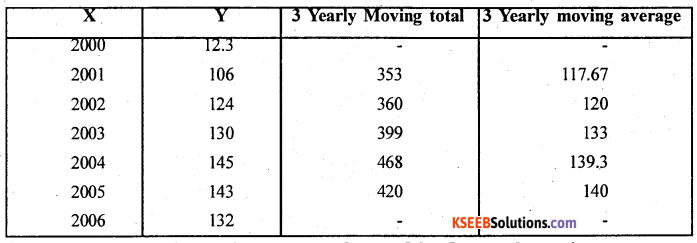
Question 5.
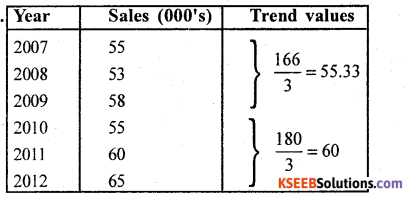
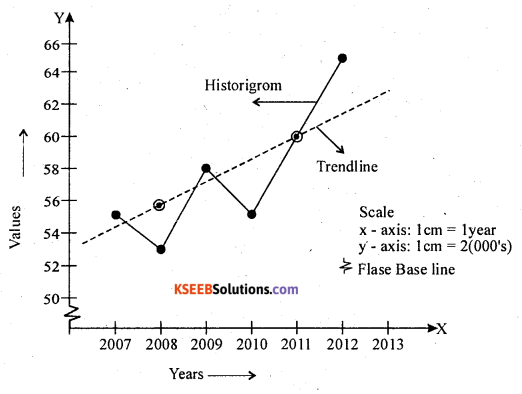
For the following time series, calculate the trend by the method of 3 yearly moving averages. Show a trend on agraph.
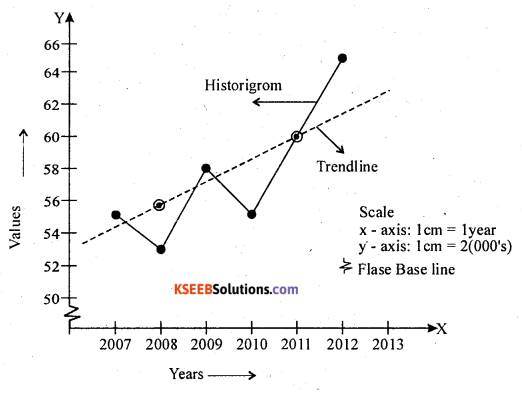

Answer:
Computation of 3 yearly moving averages.
Let x and y be the year and values of the time series.
From the graph the time series shows decreasing tendency.
Question 6.
For the following time series, calculate the trend by the method of 3 yearly moving averages. Plot the trend values on a graph.

Answer:
Calculation of trend values by 3 yearly moving averages. (Let x and y be the year and values.)
Question 7.
Calculate the trend values by finding three yearly moving averages.

Answer:
Let X and Y be the year and sales. Here the period of moving average ‘m’ = 3
Question 8.
For the following time series, conipute the trend by five yearly moving averages.

Answer:
Computation of 5 yearly moving averages. Let x and y be the year and values.
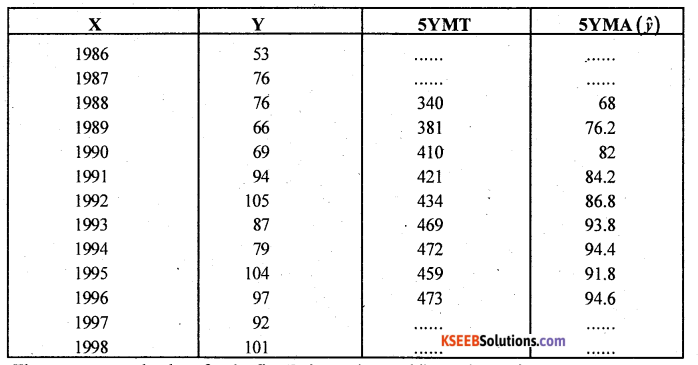
There are no trend values for the first 2 times points and last 2 times point.
(ŷ) {5 yearly moving average} trend values.
![]()
Question 9.
For the following time series, compute the trend values by the method of five yearly moving averages.

Answer:
Let x and y be the year and Index of the time series.
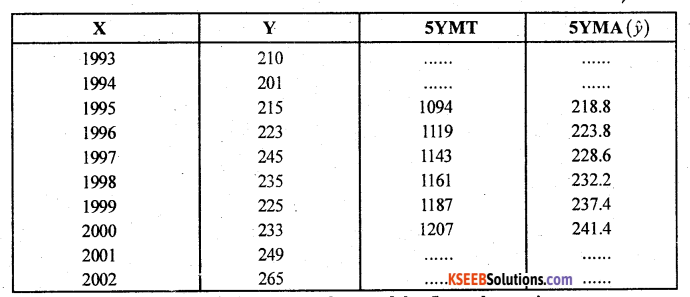
Question 10.
For the following time series, compute the trend by 5 yearly moving averages.

Answer:
Computation of trend values by the method of 5 yearly moving averages.
Let x and y be the year and values.
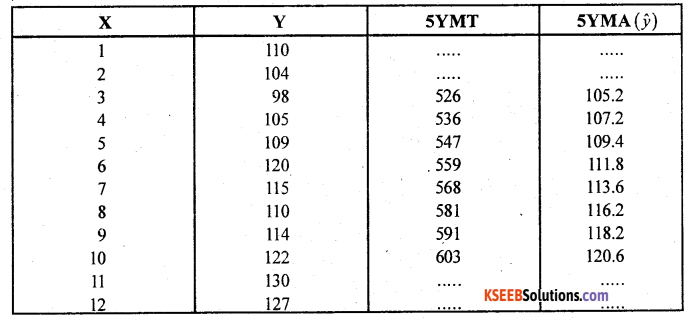
Question 11.
Obtain the trend values for the following time series by the method of four yearly centered moving averages.

Computation o ‘ 4 year y centered moving average. Let x and y be the year and values.
Here there are no trend values for the first 2 time points and last 2 time points.
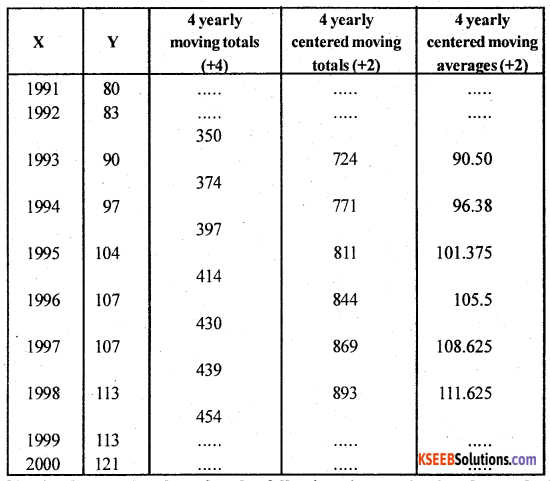
Question 12.
Obtain the trend values for the fo centered averages.

Answer:
Calculation of trend by 4 yearly moving averages. Let x and y be the year and values.
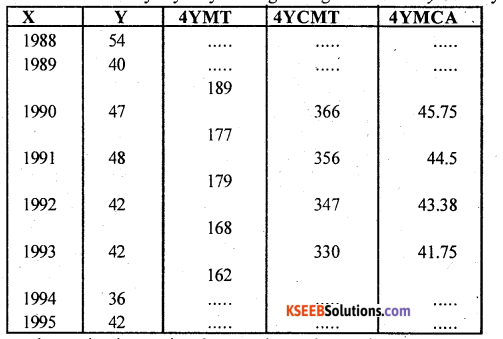
From above, the time series shows a decreasing tendency.
Question 13.
Population figures of a city (in Lakhs) are as given below. Fit a exponential curve of the type y = abx and estimate the pupulation for the year 213.

Answer:
The exponential. Logarithmetic equation isy = abx taking lagarithm on both side logy – log at x. log b.
The normal equations are:-
n log a + log b . Σx = Σ log y (1) log a lx + log b . Σx2 = Σx logy —>(2)
use deviation method and Σx = 0
let x and y be the year and population.
From (1) since Σx = 0:
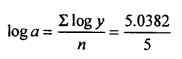
loga =1.0076
a = Antilog (1.0076)= 10.1765.
![]()
log b = 0.08684
b = A.L(0.0868) = 1.2212
The exponential trend equation is:-
y = abx
ŷ = 10,1765(1.2212)x
ŷ(2013)= 10.1-765 (1-.2212)4
Here x = 4 for the projected value for 2013
ŷ(2013) = 10.1765(2.2240) = 22.63 Lakhs.
![]()
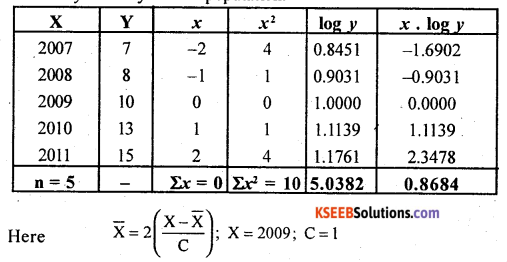
Question 14.
The production of wheat in Punjab in metric tons in a certain locality are given below. Fit a logarithmetic trend of the type y = abx and estimate the production for the year 2006.

Answer:
The exponential / logarithmic equation is
y = abx by taking logarithms
We get log y = log a + x log b
The normal equations are:-
n log a + log b Σx = Σ logy —> (1)
log a Σx + log b . Σx2 = Σx log y -» (2)
Using deviation method Σx = 0
Let x and y be the year and production of wheat.
From equation (1); since Sx = 0
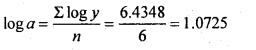
Similarly from (2)
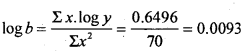
The fitted legarithmic / Exponential trend equation is; logy = log a + x log b.
i.e., logy= 1.0725 + x(0.0093)
Estimation for the year 2006; x = 6
logy = 1.0725 + 0.0093(6)
= 1.0725 + 0
logy =1.0725
and y = Anti log (log y)
= A.L (1.0725)
y = 11.82 metric tons.
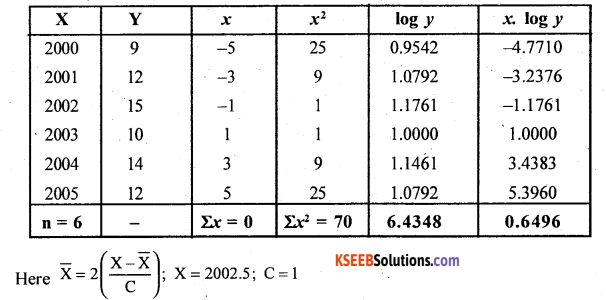
Question 15.
The sales statistics of a certain company for the years 2005 2011 are given below:

Answer:
Let x and y be the year and sdes.
the equation is : y = abx
logarithmic term: log y = log y = log a + x log b
The normal equations are:
n log a + log b Σx = Σ log y -> (1)
log a . Σx + log b . Σx2 = lx . log y —> (2)
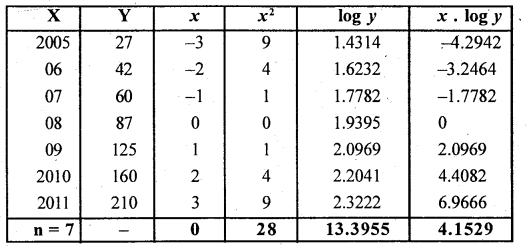
From equation (1) since Ex = 0
![]()
loga= 1.9136 a = AL(1.9136) = 81.9596
![]()
log b = 0.1483 b = AL (0.1483) = 1.407
The fitted exponential equation is:-
y = abx
ŷ = 81.9596(l.407)x
Estimation for the year 2012; x = 4
ŷ(2012)= 81.9596(1.407)4
= 81.9596 x 3.919 = 321.199 units.
Question 16.
For the given time series, fit a straight line trend of the type y = a + bx by the method of least squares.

Answer:
Let x and y be the year and production.
The straight line equations y = a+bx
Normal equations are.
na + b Σx = Σ y ……..(1)
a Σx + b Σx2 = Σxy……..(2)
Here x = X – x̄( odd time points)
x̄ = 1996
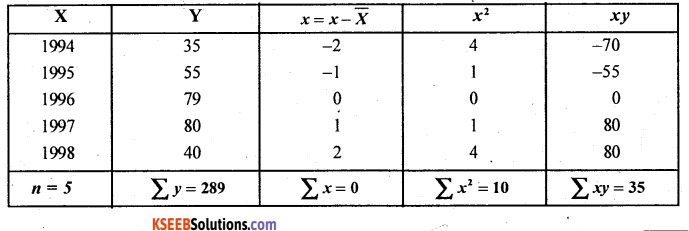
From (1) 5a + b. 0 = 289
∴ a = \frac{289}{5} = 57.8
From (2) a.0 + b.10 = 35
∴b = \frac{35}{10} = 3.5
Hence the fitted straight line trend equation is ŷ = 57.8 + 3.5x
Note: The trend values for the givjgn years can be obtained by substituting the values of x as -2, -1, 0, 1, 2 if n is odd and -5, -3, -1, 1, 3, 5 if n is even.
![]()
Question 17.
Fit an equation of the type y = a + bx to the following Time-series data.

Answer:
The straight line equation is y = a + bx
The normal equations are na + b Σx = Σy
a Σx+b Σx2= Σ xy
Here n = 8, even,
take x=2 (x- x̄); x̄ = 2001.5
Let X be the year and Y be the imports.

The fitted straight line equation is : ŷ = 30.875 -0.375x
Question 18.
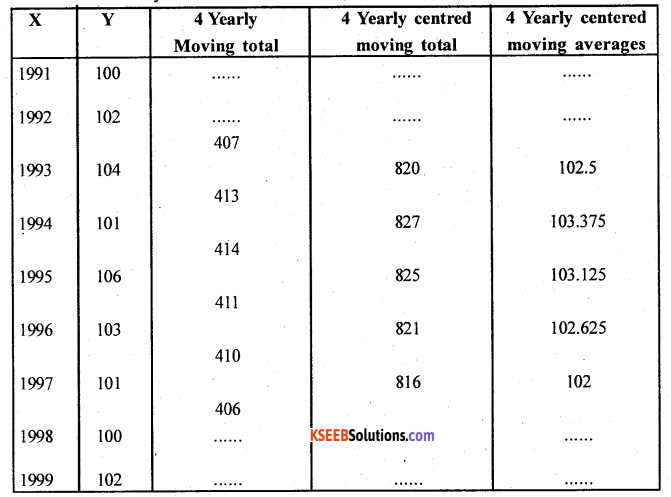
Compute 4 yearly moving averages for the following data :

Answer:
Let X and Y be the years and values
2nd PUC Statistics Time Series One and Ten Marks Questions and Answers
Question 1.
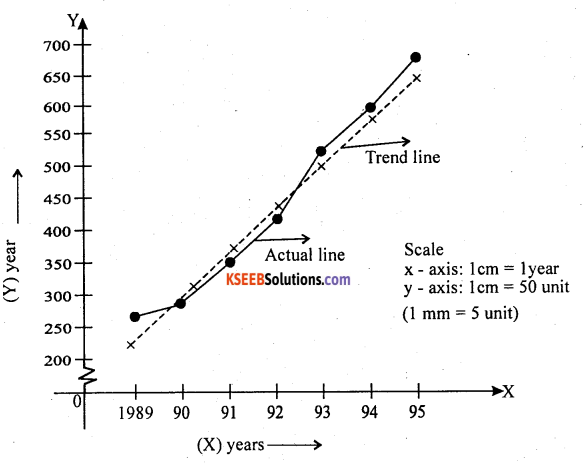
Fit a straight line to the following time series, show the trend line on a graph

Answer:
Let x and y be the year and values The Straight line equation is
y = a + bx
Normal equations are –
na + bΣx = Σy ………… (1)
aΣx + bΣx2 = Σxy ………….(2)
Here x̄ = 1992
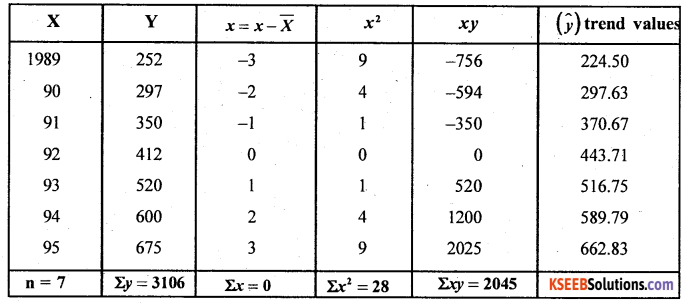
From (1) 7a + b.O = 3106
∴ a = 443.71
From (2) a.O + b.28 = 2045
∴ b= 73.04
∴ The fitted straight line trend equation is
ŷ = 443.71 + 73.04x
Trend value (ŷ) for 1989; Here x = -3
∴ ŷ 1989 = 443.71 + 73.04 (-3) = 443.71 – 219.12
ŷ 89 = 224.50
Trend value for 1990 ; Here x = -2
ŷ 90 = 443.71 + 73.04(-2) = 297.63
Similarly all remaining trend values can be obtained by substituting x= -1,0,1,2 and 3 Straight line trend:
Question 2.
For the given time series, fit a straight line trend of the type y = a + bx by the method of least squares and find the trend value for the year 1995.

Answer:
X Here X=2(x-x) \n = 6 X = 1990.5
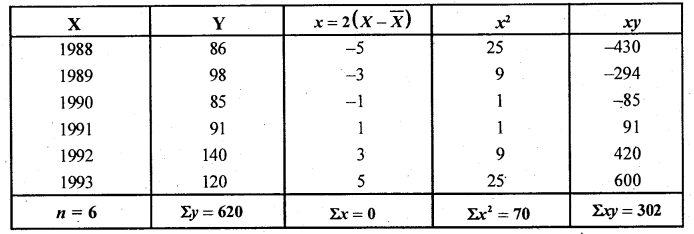
From (1) 6a + b.0 = 620 ∴ a = 103.33
From (2) a.O + b.70 = 302 ∴ b = 4.31
The fitted straight line trend equation is.
ŷ = 103.33 + 0.057x
Estimation of production for the year 1995
Here x = 9
ŷ1995 = 103.33 + 4.31(9)= 142.09.
![]()
Question 3.
For the following time series fit a curve of the type y = a + bjc + cx2. Estimate the value for 1997.

Answer:
The quadratic equation is:
y = a + bx + cx2
The normal equations are
na + bΣx + cΣx2 = Σy ………..(1)
aΣx + bΣ2+cΣx3 = Σxy………..(2)
aΣx2 + bΣ3+cΣx4 = Σx2y………..(3)
Here x = X – X̄
Let x and y be the year and the value
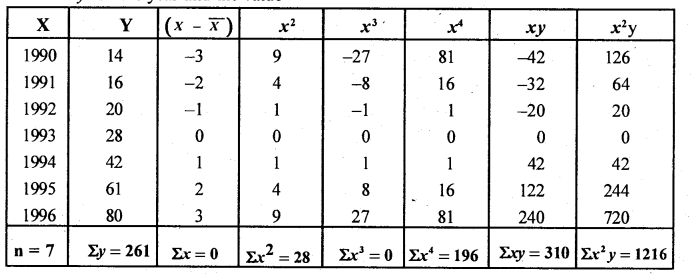
From (1) 7a + b.0 + c.28 = 261
7a + 28c = 261 ………….. (4)
From (2) a.0 + b.28 + c.0 = 310
b= 11.07
From (3) a.28 + b.0 + c.196 = 1216
28a + 196c = 1216 ………….(5)
Solving (4) and (5) we get a and c
4 x (4) – (5)
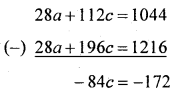
∴ c = 2.05
Put c = 2.05 in (4) we get
7a + 28(2.05) = 261
7a = 261 – 57.4
∴ a = 29.09
The trend equation is: ŷ = 29.09 +13.57x+2.05x2
Estimation for the trend value for 1997
Here x = 4 ; x2 = 16
ŷ1997 = 29.09 +11.07 (4) + 2.05(16)
ŷ1997 = 106.17.
Question 4.
Fit a quadratic trend of the form y = a + bx + cx2 to the following time series.

Estimate the probable number of merited students in the college in the year 1995.
Answer:
The Quadratic equation is y = a + bx + cx2
The normal equations are – na + bΣx + cΣx2 = Σy
aΣx + bΣx2 + cΣx3 = Σxy
aΣx2 + bΣx3 + cΣx4 = Σx2 y
Let x and y be the year and no. of merited students X̄ = 1992
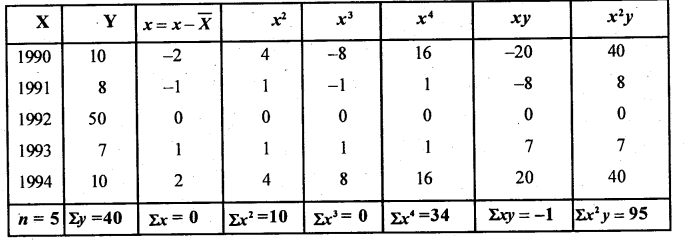
From (1) 5a + B.0 + c.10 =40
i.e. 5a + 10c = 40 (4)
From (2) a.0 + B.10 + c.0 = -1
∴ b = – 0.1
From (3) a.l0 + B.0 + c.34 = 95
i.e. 10a + 34c = 95………….(5)
Solving (4) and (5) we get a and c ;(4) x 2 – (5)
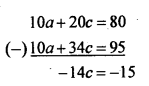
∴c = 1.07
Substituting c = 1.07 in (4)
we get 5a+10(i.07) = 40
∴ a = 0.17
The fitted quadratic trend equation is
ȳ = 0.17 – 0.1x + 1.07x2
Estimation for 1995 Here x = 3, x2 = 9
ȳ95 =0.17 — 0.1(3) +1.07(9)
∴ ȳ95 = 9.5
![]()
Question 5.
Fit a quadratic trend for the following time series. Estimate the population for the year 2011.

Answer:
Let x and y be the year and population. The quadratic equation is –
y = a + bx + cΣx2
Normal equations are na + blx + clx2 = ly
alx + bΣx2 + cΣx3 = Σxy aΣx2 + bΣx3 + cΣx4 = Σx2y
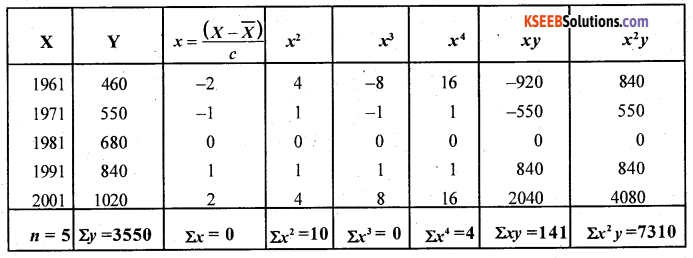
From (1) 5a + b.0 + c.10 = 3550
i.e. 5a + 10c = 3550 -(4)
From (2) a.0 + 6.10 + c.0 = 1410
∴ b = 141
From (3) a.10 + b.0 + c.34 = 7310
i.e. 10a + 34c =7310 (5)
By solving (4) and (5) we get a and c
(4) x 2 – (5)
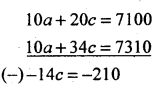
∴ c = 15
Substitute c = 15 in (4)
we get 5a +10(15) = 3550 ∴ a = 680
The fitted quadratic trend equation is
ŷ = 680 + 141x + 15x2
Estimation of the population for the year 2011 Here x = 3, 2 = 9
ŷ2011 = 1238millions.