You can Download Chapter 8 Operation Research Questions and Answers, Notes, 2nd PUC Statistics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Statistics Question Bank Chapter 8 Operation Research
2nd PUC Operation Research One and Two Marks Questions and Answers
Question 1.
Define Operations research
Answer:
“It is the method of application of scientific methods, techniques and tools to problems involving the operations of a system, so as to provide those in control of the system with Optimum solutions to the problem.”
Question 2.
Mention a method of solving Linear Programmings Problems
Answer:
Graphical method.
Question 3.
Define L.P.P
Answer:
Linear programming is a mathematical technique, which deals with the optimization (Maximization or Minimization) of activities subject to the available resources.
Question 4.
Mention two areas where the economic operations research can be applied/Uses of Oprations of Research
Answer:
Linear programming problems are used in Industries for effective use of men, machine, money and Material. Game theory is applied in conflicting situations, to suggest the best strategy. Replacement Problems helps in suggesting the best time period to replace a specific part in manufacturing process, and Inventory problems help in organizing stocks and maintaining costs, and so on.
Question 5.
Define a solution for a LPP?
Answer:
A set of real values X = (x1 x2, x3, …xn), which satisfies the constraints AX(≤ = ≥)b, is called a Solution.
![]()
Question 6.
What is a feasible solution in a L.P.P?
Answer:
A set of real values X = (x1, x2, x3, ……. xn), which satisfies-
- The constraints AX(≤ = ≥)b and
- The non-negativity restriction x > 0
Question 7.
Define optimal solution in an L.P.P.
Answer:
A set of real values X = (x1, x2, x3, …xn), which satisfies,
- The constraints AX(≤ = ≥)b
- The non-negativity restriction x ≥ 0 and
- Optimizes the objective function Z = CX is called optimal Solution
OR If a feasible which optimizes the objective solution Z = CX is called optimal solution
Question 8.
Define Multiple Optimal solution in LPP.
Answer:
An LPP is said to have Multiple Optimal Solution if has more one Optimal Solutions.
Question 9.
When unbounded solution exist for a given L.P.P?
Answer:
For some LPP the optimum value of Z may be infinity, then LPP is said to have unbounded solution.
Question 10.
When an L.P.P is said to have no solution?
Answer:
In a LPP if all the constraints cannot be satisfied simultaneously then there exists no solution
Question 11.
Why the feasible solution can exists only on xy-plane / Why the solution to the LPP lies in the first Quadrant?
Answer:
For the given LPP, the solution can exists only on xy-plane, because of the non-negativity restrictions, x and y both are positive on xy-plane
Question 12.
In an L.P.P objective functtin is Max Z = 20x + 70y and if solution are A(0,8) and B(12,5). Find optimal solution.
Answer:
ZA = 20(0) + 70(8) = 560; and ZB = 20(12) + 70(5) = 590 (max)
∴ Optimal soplution is at B(12,5); is x = 12 and y = 5
Question 13.
Is an optimal solution always a feasible solution? (In L.P.P)
Answer:
Yes
Question 14.
Define/ what is a game?
Answer:
’’Whenever there is a situation of conflict and competition between two or more opposing teams, We refer to the situation as a game”
Question 15.
Write any two properties of a Game/Rectangular Game
Answer:
- there are finite numbers of players
- Each player have finite number of courses of action OR The game is said to be played, one of the player should adopt one of course action while playing the game.
Question 16.
Define/Explain /What is meant by a rectangular game/2-person zero-sum game?.
Answer:
In a game of two players, the gain of one player is the loss of the other.
Question 17.
Define ’strategy’ in a game.
Answer:
The strategy of player is the predetermined rule by which he chooses his course of action while playing the game
Question 18.
Define the term pure strategy
Answer:
While playing a game, the pure strategy of a player is the predetermined decision to adopt a specified course of action irrespective of the course of action of the opponent
Question 19.
What do you mean by a mixed strategy in 2-person-zero-sum game?
Answer:
While playing a game, mixed strategy of a player is his pre-decision to choose his course of action according to certain pre-assigned probabilities
Question 20.
Explain the maximin and Minimax of the game
Answer:
- Maximin is the maximum of row minimums of the payoff matrix, (α)
- Minimax is the minimum of the column maximums of the payoff matrix (β)
![]()
Question 21.
What is a saddle point?
Answer:
Saddle point is the position where Maximin and Minimax coincide
Question 22.
What is the Principle of Dominance?
Answer:
If the strategy of a player dominates over the other strategy in all conditions, then the latter Strategy can be ignored, because it cannot affect the solution in any way.
Question 23.
In a two person zero-sum game, the value ν = -1, is the game fair?
Answer:
The game is not fair, (the game is said to be fair if ν = 0)
Question 24.
What is meant by pay-off in a rectangular game?
Answer:
It is the gain or loss of the players while playing a game.
Question 25.
In a game if ν = 2 then what are the values of α & β?
Answer:
Here α – Maximin and β – Minimax are equal and are equal to ν = 2.
Question 26.
In a rectangular game, the gain of player – A is 5. Then what is the Gain/Loss of the other player – B?
Answer:
Loss = – 5
Question 27.
Calculate E.O.Q Given D/R = 5000 units/month, C1 = Rs.lO/month, C3 = Rs.200/ month.
Answer:
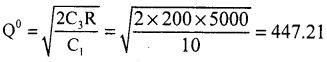
Question 28.
In a rectangular game pay-off matrix of player A is:
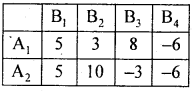
Write down the pay-off matrix of player B
Answer:
The pay-off matrix of player B is:
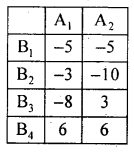
Question 29.
For the following pay-off matrix of A. Write down the pay-off matrix of B
Answer:
The pay-off matrix of player B is:

Question 30.
What do you mean by a replacement problem?
Answer:
Replacement problem is the problem of deciding the age at which old equipments (machine and their spare parts, trucks etc.) are replaced.
Question 31.
Give any two needs/uses of replacement of equipment which deteriorate with age
Answer:
New equipments are more efficient. Maintenance/Operating cost and production cost is less than old ones.
Question 32.
When the equipment, which deteriorates with age, is replaced? /What is the principle adopted for the replacement of equipment which deteriorates with age?
Answer:
When its Annual average cost: A(n) is minimum, at that age the equipment which deteriorates with age should be replaced.
Question 33.
When do you suggest the optimal age for replacement of equipment?
Answer:
When its Annual average cost A(n) ceases to decrease arid starts to increase, that is point of time is to replace. OR Where Annual average cost A(n) is least we suggest to replace the old machine by new one.
Question 34.
Specify the needs for replacement of capital equipment
Answer:
- As the equipment grow older, its maintenance cost would be costlier.
- Production cost would be lesser in new equipments.
Question 35.
If the depreciation cost and the cumulative maintenance cost for equipment for the second year are Rs.10000 and Rs.10200 respectively. What is the annual average cost?
Answer:
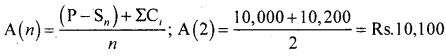
![]()
Question 36.
What do you mean by Inventory?
Answer:
An Inventory is a physical stock of goods, which is held for the purpose of future production or sales.
Question 37.
What is an Inventory Model?
Answer:
A set of mathematical equations required to solve the inventory problems is called an Inventory model.
Question 38.
What is EOQ/E.L.S?
Answer:
It is the size/lot of the order in which the ‘set up cost’ and ‘holding cost’ of the Inventory is minimum.
Question 39.
Mention any two essentials/needs/advantages of an Inventory.
Answer:
- It helps in smooth and efficient running of the business.
- It provides adequate and satisfactory service to the customers.
- It facilitates bulk purchase of raw materials at discounted rates.
Question 40.
Give any two disadvantages of the Inventory?
Answer:
The Disadvantages of Inventory are warehouse rent, labour of maintenance, loss due to fall in price, deterioration of goods should be incurred
Question 41.
Explain
1. Lead time-t
2. Holding cost-C1
3. Set up cost-C3
4. shortage cost-C2
Answer:
Lead time – t: The time gap between placing of order and arrival of goods at the inventory is the Lead time
Holding cost – C1: It is the cost associated with carrying or holding the goods in stock until the goods are sold or used. It includes rent for space, interest on capital, maintenance of records, taxes, insurance etc.
Setup cost – C3: It is the cost of setting up the machines for production or the cost of 4 placing the order for the goods. It includes labour cost, transportation cost etc. It is also called as Ordering cost.
Shortage cost – C2: The cost associated with delay or inability to meet the demand, because ^ of shortage of Stock is called shortage cost Or penalty cost.
Question 42.
When an L.P.P. is said to have no solution?
Answer:
In an L.P.P. if all the constraints cannot be satisfied simultaneously then there exists no solution.
Question 43.
Comment: The graphical solution to the L.P.P. lies in the I Quadrant.
Answer:
Due to the non-negative restriction X ≥ 0 which satisfy that feasible solution can lie only in the I Quadrant.
Question 44.
In a Two-person-zero-sum game, the value of the game V = -1 is it a fair game?
Answer:
The game is said to be fair if V = 0. Here V = -1.
∴ It is not a fair game.
Question 45.
What is meant by value of a game?
Answer:
The payoff at the saddle point is known as value of the game denoted by ‘V’.
![]()
Question 46.
When is a game said to be fair?
Answer:
When value of the game V = 0.
Question 47.
What is principle of dominance?
Answer:
If the strategy of a player dominates over the other strategy in all conditions, then the latter strategy can be ignored.
Question 48.
What is meant by pay-off in a rectangular game?
Answer:
The gain or loss between the players while playing a game is called pay off.
Question 49.
Write down the formula for calculating Annual average cost of an item/equipment.
Answer:
The annual average cost : A(n) = \(\frac { T }{ n }\)
Total cost T = (P – Sn) + Σ Ci.
Where P – Purchase cost
Sn – Resale/ {Scrap Value}
Ci – Maintenance cost.
Question 50.
What are the uses of replacement of equipment which deteriorate with age?
Answer:
New equipments are more efficient. With adoption of new technology, maintenance cost (Operating cost) and production cost would be less than the old ones.
Question 51.
If in a game the -saddle point’ is 5, what is the value of ‘mini-max’?
Answer:
Value of ‘mini-max’ is ‘5’ (because saddle point is the position where maximin and minimax coincide i.e. α = β = ν.
Question 52.
Mention two areas where the economic operations research can be applied.
Answer:
Operations Research can be applied in L.P.P as production management, marketing management, replacement problems helps in suggesting the best time to replace a machine etc.
Question 53.
Write down the L.P.P. model.
Answer:
Optimize Z = CX
Subject to constraints AX (≤ = ≥) b.
and non-negativity restriction X ≥ 0.
Question 54.
Solve the game.

Answer:
By maximin – minimax principle.
(i) Row minimums are circled. (ii) Column maximums are boxed.
Here the payoff 5 is circled as well as boxed.
The saddle point occurs at (1, 1)
The suggested solution is pure strategy
i.e., For player A – A1
For player B – B1,
value of the game V = 5.
Question 55.
Solve the following game Player A
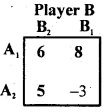
Answer:
Using principle of dominance.
All elements (payoffs) of A1 row are more than A2
i.e. A1 dominates A2 delete A2
6 is less than 8, i.e., B1 dominates B2 delete B2.
Value of the game V = 6.
The suggested strategy is pure strategy.
For player A – A1 and for B – B1 OR
Solve using maximin – minimax priniple.
![]()
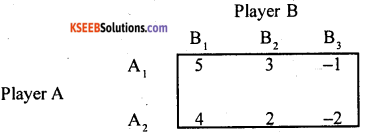
Question 56.
In a two-person-zero-sum game the pay off matrix of player A is given below.
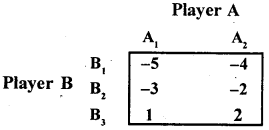
Write the payoff matrix of player A.
Answer:
Here Row elements are written as columns elements by changing signs, with respective strategies and players.
∴ The pay off matrix of player A is:
Question 57.
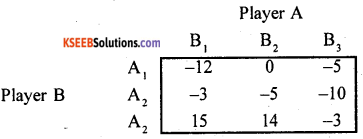
In a rectangular game the pay off matrix of player A is –
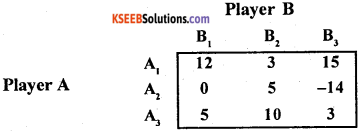
Write down the pat off matrix of player B is –
Answer:
Here row elements are written as column elements by changing signs, with response strategies and players. The pay off matrix of player B is –
Player A
Question 58.
What is meant by equipment which deteriorates with age? Give an example.
Answer:
As equipment become older, they deteriorate i.e., they become less efficient, and their maintenance cost increases. Ex : Motor Bike.
Question 59.
The cumulative maintenance cost of a machine during fourth year is Rs.13,400. Its purchase cost is Rs. 8,500. Find the average annual cost assuming that the machine has no resale value.
Answer:
Average annual cost : A(n) = \(\frac { T }{ n }\)
Here T = (P – Sn + ΣCi
\(A(4)=\frac{8500+13400}{4}=R s .5475\)
Question 60.
What is the need of Inventory in a business concern?
Answer:
An inventory is essential for smooth and efficient running of the business. By bulk purchasing of goods required at discounted rates, adequate and satisfactory service can be given to the customers and can earn more profit.
Question 61.
What are the disadvantages of the inventory?
Answer:
The inventory has disadvantages such as ware house rent, labour of maintenance, loss due to fall in price, deterioration of goods, etc., should be incurred.
Question 62.
Write down the formulae for the following in Inventory model I (without shortages) (a) EOQ (b) Minimum Average Cost.
Answer:
(a) EOQ / ELS = Q° = \(\sqrt{\frac{2 \mathrm{C}_{3} \mathrm{R}}{\mathrm{C}_{1}}}\)
(b) Minimum Average cost = \(\sqrt{2 \mathrm{C}_{1} \mathrm{C}_{3} \mathrm{R}}\)
Question 63.
Write down the formulae for the following inventory model II (with shortage cost)
(a) EOQ
(b) Minimum average cost
Answer:
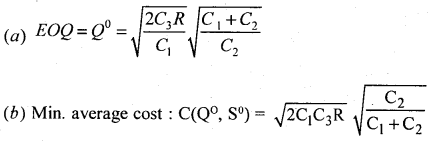
Question 64.
What are optimal lot size and maximum inventory level in the Inventory model II.
Answer:
ELS/EOQ : Q°= \(\sqrt{\frac{2 \mathrm{C}_{3} \mathrm{R}}{\mathrm{C}_{1}}} \sqrt{\frac{\mathrm{C}_{1}+\mathrm{C}_{2}}{\mathrm{C}_{2}}}\) and Maximum inventory level : S° = \(\frac{\mathrm{c}_{2} \mathrm{Q}^{0}}{\mathrm{c}_{1}+\mathrm{C}_{2}}\)
Question 65.
If R = 7000/year, C1 = Rs. 2 per unit/year and C3 = Rs. 75. Find the optimum lot size and optimum number of orders.
Answer:
Since shortages are not given use Model II .
Optimum lot size are;
\(Q^{0}=\sqrt{\frac{2 C_{3} R}{C_{1}}}=\sqrt{\frac{2 \times 75 \times 7000}{2}}\)
Q° = 724.57 ≈ 725 units.
Optimum no of orders : \(\mathrm{n}^{0}=\frac{\mathrm{R}}{\mathrm{Q}^{0}}=\frac{7000}{725}\) ∴ n° = 9.67 ≈ 10 orders
![]()
Question 66.
Find the EOQ and minimum average cost for the following data.
Annual demand = 1000 units.
Cost of an unit = Rs. 20
Ordering cost = Rs. 2 per order
Holding cost = 15% per year
Answer:
Given: R= 1000, P = 20, C3 = 2, I = 15%
∴ C1 = PI = 20 × 15% = 3.
EOQ : \(Q^{0}=\sqrt{\frac{2 C_{3} R}{C_{1}}}=\sqrt{\frac{2 \times 2 \times 1000}{3}}=36.51\)
∴ Q° = 37 units
Minimum average cost C(Q°) = \(\sqrt{2 \mathrm{C}_{1} \mathrm{C}_{3} \mathrm{R}}=\sqrt{2 \times 3 \times 2 \times 1000}=109.54 \simeq 110\)
Question 67.
Find EOQ for the data given below.
R = 100 units per day
C3 = Rs. 50 per order
A1 = Re. 1 per unit/day
C2 = Rs. 10 per unit/day.
Answer:
Here shortage cost (C2) is given, use EOQ model II and all information is given per day.
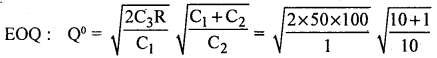
∴ Q°= 104.9 = 105 units.
Question 68.
Find minimum average inventory cost for the following data :
R = Rs. 150 per month
C1 = Rs. 1.50 per unit per month
C2 = Rs. 5 per unit per month
C3 = Rs. 25 per order.
Answer:
Minimum average inventory cost is
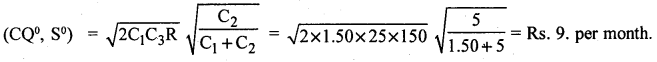
Question 69.
Given :
Set up cost = Rs. 50 / cycle
Storage cost = Rs. 3 / item/ year
Demand = 5000 items/year
Calculate ‘minimum average inventory cost’.
Answer:
Given R = 5000 items / year
C1 = Rs. 3 / item / year
C3 = Rs. 50/ cycle
Minimum average inventory cost is :
![]()
Question 70.
The objective function and two solutions of an L.P.P. are : maxz = 200x + 100y and A (0, 5), B(10, 7). Find the optimal value of z.
Answer:
For A (0,5): Max z =200(0)+ 100(5)
z =500
For B(10, 7): Max z =200(10)+100(7)
z =2700
The optimal value of z =2700.
Question 71.
If the depreciation cost and the cumulative maintenance cost for an equipment for the third year are Rs. 6,000 and Rs. 6,200 respectively, what is ‘Annual Average Cost’?
Answer:
Annual Average Cost
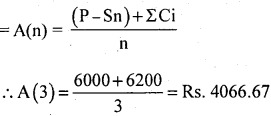
2nd PUC Operation Research Five Marks Questions With Answers
Linear Programming Problems
Question 1.
A manufacturer produces 2 products A and B which needs two machines P and Q. Product A requires 6 hours on machine P and 2 hours on machine Q. Product B requires 4 hours on machine P and 4 hours on machine Q. There are 100 hours of time available on machine P and 80 hours on machine Q. Profit earned by the manufacturer on selling one unit of A is Rs.10 and on selling one unit of B is Rs.15. Formulate L.P.P. ,
Answer:
Let x be the number of units of product A Sold
and y be the number of units of product B sold
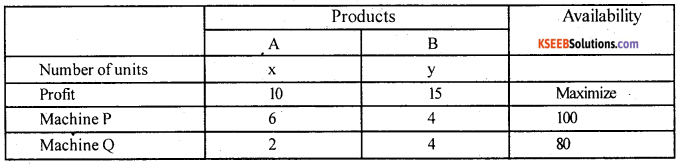
Then, the L.P.P is –
Maximize Z = 10x + 15y
Subject to 6x + 4y ≤100
2x + 4y ≤ 80
and x ≥ 0, y ≥ 0.
Question 2.
A firm produces two types of cloth, printed and plain. Three kinds of yarns are required to produce the cloth – red, green and blue. One unit length of printed cloth needs 2 metres of red yarn, 6 metres of blue yarn and 4 metres of green yarn. One unit length of plain cloth needs 5 metres red yarn. The firm has a stock of 8 metres of red yarn, 10 metres of green yarn and 15 metres of blue yarn. It is assumed that income obtained from one length of printed cloth is Rs. 10 and one length of plain cloth is Rs. 6. Formulate the L.P.P. so as to maximise the income obtained from the sale of finished product.
Answer:
The L.P.P. is :
maximize Z = 10x + 6y
Subject to constraints : 2x + 5y ≤ 8
6x ≤ 10
4x ≤ 15
and x ≥ 0, y ≥ 0.
![]()
Question 3.
A company manufactures two products X & Y. Due to deficit of raw materials not more than TOO units of X and 200 units of Y can be produced in a month. Total labour available is 600 hrs per month. Each unit of X requires 2 hrs and each unit of Y requires 4 hrs to be produced. If the profit obtained by selling one unit of X is Rs. 50 and one unit ofY is Rs. 100, formulate an LPP.
Answer:
The linear programming problem is :
Max. Z = 50x + 100y
Subject to x ≤ 100
y ≤ 200
2x + 4y ≤ 600 and
x ≥ 0, y ≥ 0.
Question 4.
Solve the following L.P.P graphically.
Maximize Z = lOx + 5y
Subject to 2x + 4y ≥ 20.
x + 2y ≤ 30
and x, y ≤ 0.
Answer:
The constraints should be represented graphically.
Write each constraints as equalities and are represented by straight lines by finding two points on each of these lines.
Consider,
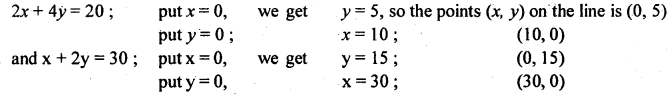
The equations are graphically represented as below :
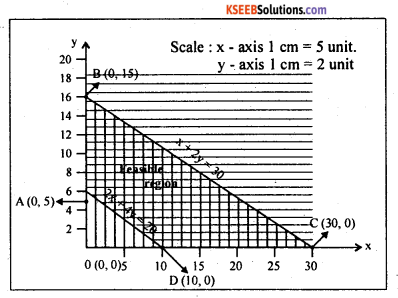
The common shaded area is the feasible region. The corner points of the feasible region A(0,5), B(0,15) C(30,0) and D(10,0)
The Z values at these corners points are tabulated as below:

Since ‘Z’ is to maximize and which maximizes at these corner points C(30,0)
∴ The optimum solution is x = 30, y = 0
The optimum (maximum) value of Z is 300.
Question 5.
For the following. L.P.P obtain the solution graphically. .
Maximize Z = 50x1 + 100 x2
Subject to the constraints
10x1 + 5x2 ≤ 2500
4x1 + 10x2 ≤ 2000
and x1 ≥ 0, X2 ≥ 0.
Answer:
The constraints should be represented graphically.
Write each constraints (inequalities) as equalities (equation) and represent these equations as straight lines by finding two points on each of these lines.
Consider,
10x1 + 5x2 = 2500 ;
put x1 = 0 ;
we get x2 = 500,
So, the points (x, y)/(x1 x2) on the line is (0, 500)
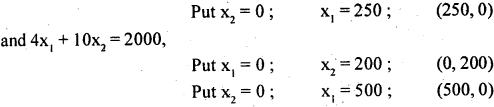
The equations are graphically represented as below:
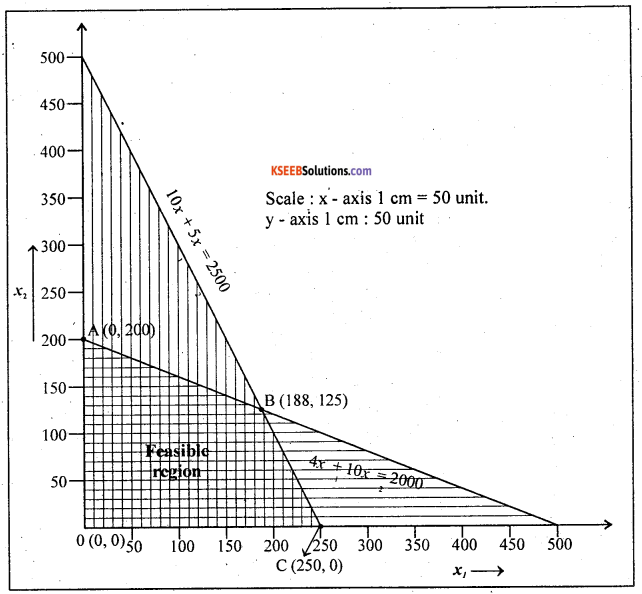
The Common shaded area is the feasible region. The corner points of the feasible region are 0(0, 0), A (0,20), B( 188, 125), C(250,0)
The Z-values at these corner points are tabulated as below:

Since Z is to maximize and which maximizes at the comer point B (188, 125)
∴ The optimum solutions is x1 = 188, x2 = 125.
The optimum (maximum) value of Z is 21900.
![]()
Question 6.
Graphically solve the L.P.P.
Maximize Z = 2000x + 4000y
Subject to x – 2y ≥ 10.
x + 2y ≤ 30 ;
x, y ≥ 0.
Answer:
The given constraints should be represented graphically.
Write each constraints as equalities (equations) and represent as straight lines after finding two points on each of the lines.
Consider,
x – 2y = 10 ; Put x = 0 ; we get y = -5, So, the points (x, y) on the line is (0, – 5)
Equations are graphically represented as below:
(Here one of the point of y is -ve. So, consider the -ve y-axis and feasible region can occur only at x, y axis (as x and y are +ve) due to the non-negativity restriction)
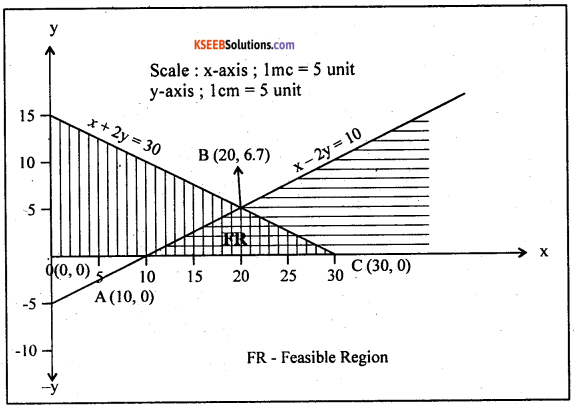
The common shaded area is the feasible region. The corner points of the feasible region as A(10,0) B(20, 6.7) and C(30, 0)
The Z – values at these 7 corner points are tabulated as below:

since Z is to maximize and is maximizes at the corner points B(20,6.7)
∴ The optimum solution is x = 20 y = 67
The optimum value of Z is 66800.
Question 7.
Solve the following linear programming problem, graphically
Max z = 10x + 3y
Subject to constraints 2x + 3y ≥ 3
x + 2y ≤ 4
and x ≥ 0, y ≥ 0
Answer:
Consider the constraints as equalities and represent by graphically as straight line.
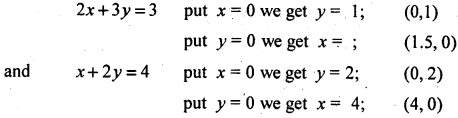
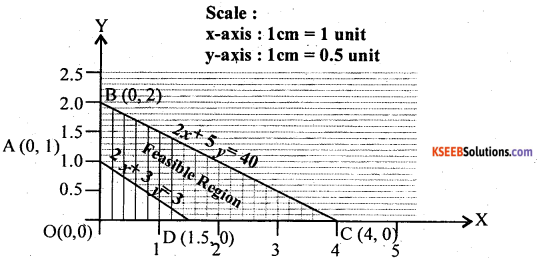
From the graph the corner points of the feasible region are A(0,1), B(0,2), C(4,0) and D(1.5,0)
The values of z at these corner points are :
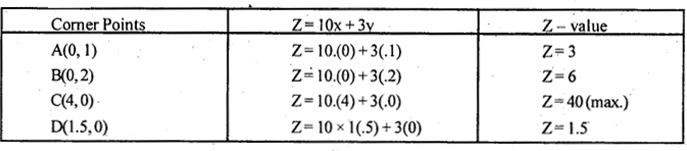
The maximum value of z occurs at C(4,0)
The optimum solution to the L.P.P is x = 4, y = 0 ; The optimum cost = 40
Transportation Problems
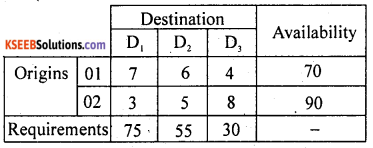
Question 1.
For a transportation problem with cost matrix as given below:
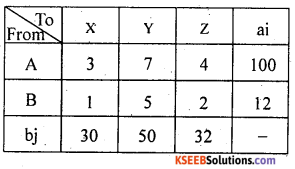
Find a solution by north west corner rule and find transportation cost.
Answer:
Here the availability; ai = requirement; bj = 112, thus the T.P. is balanced. Therefore there exists a feasible solution.
Consider the north west corner cell at (1, 1) allocate as; minimum (a,, b,) = min (100, 30) x11 = 30.
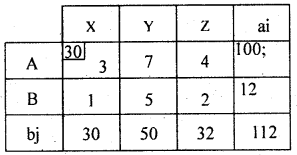
Here a1 > b1 and replace b1 = 100 – 30 = 70.
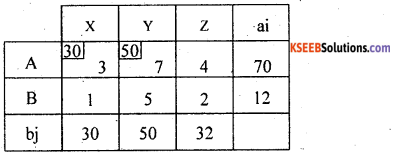
Next, Allocate at (1,2) as: Min (70, 50) = 50; X12 = 50.
Here again a1 > b1 and replace, b1 = 70 – 50 = 20.
Next allocations meat (1,3) as; min (20, 32) = 20 and replace (32 – 20) – 12 A; So, X13 = 20.
Next allocation is mode at (2, 3) as:
Here b3 > a1 So, Min (12, 12) = 12 ; X23 = 12.
All allocations are made. Thus, initial feasible solutions is:-
X11 = 30, X12 = 50, X13 = 20, X23 = 12
The transportation cost is: Z = ΣΣCij.Xij
= 3 × 30 + 7 × 50 + 4 × 20 + 2 × 12 = 90 + 350 + 80 + 24 = Rs. 544.
Note: In the problem m(rows) = 2, n(Columns) = 3
∴ m + n – 1 = 2 + 3 – 1 =4
The number of allocations = 4 is same as (m + n – 1). The initial feasible solutions a basic feasible solution.
![]()
Question 2.
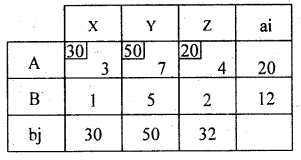
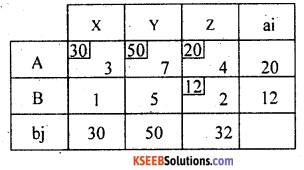
Find the Initial basic feasible solution by matrix minimum method for the following T.P.
Answer:
By matrix minimum method / least cost entry method let allocation is made at the least cost at (2, 1) as: X21 = Min (90, 75) = 75
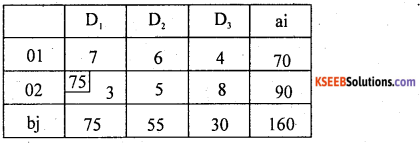
Write down the reduced matrix after deleting ‘D1’ – destination.
Replace. b2 = 90 by (90 – 75) = 15
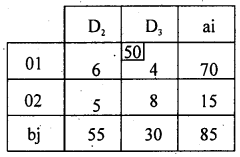
The lowest cost in the reduced cost matrix is 4 at (1, 2) / (D1 D3).
Allocate as X13 = Min (70, 30) = 30
Delete D3 – destination and replace 70 by (70 – 30) = 40
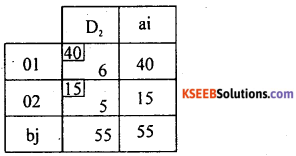
The lowest cost in the reduced cost matrix is 5 at (2, 2) OR (O2, D2) Allocate as X22 – Min (15, 55) = 15 and replace 55 by (55 – 15) = 40.
So, the Final allocation is at the cell (1, 2) / (D1, D2):
Allocate as X12 = min (40, 40) = 40. Thus all allocations are made as below:
From the original table.
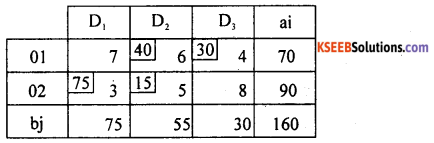
Observe O, availabilities are distributed to D2 and D3 and O2 availabilities are distributed to D1 and D2, total availabilities are allocated to required destinations as : X12 = 40, X13 = 30, X21 = 75, X22 = 15 and the total transportation cost is:
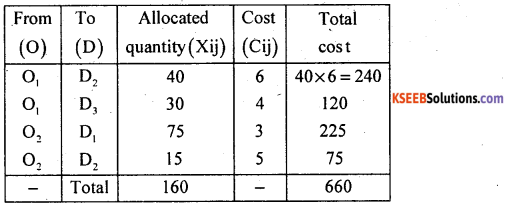
∴ Total transportation cost is Rs. 660/- is the basic feasible solution for the given T.P.
Note: In the above problem: number of rows: m = 2; number of columus ;
n = 3(m + n- l) = (2 + 3- l) = 4.
Number of allocations = 4. Both are some, the solution is degenerate.
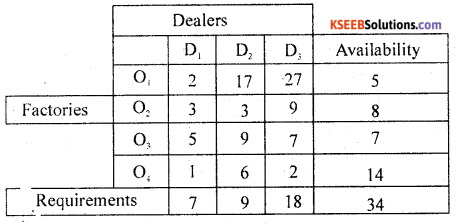
Question 3.
For the following transportation problem, obtain the Initial basic feasible solution by:-
1. N.W.C.R and
2. Matrix minima method (M.M.M)
Answer:
1. By N.W.CR:- Start allocating at north corner cell at the cell (1, 1):
X11 = Min (a1 b1)
= min (5, 7) = 5
Here O1 is satisfied, next allocate at (2, 1) as:
X21 = Min (a2, b1 – X11) = Min (8, 7-5)
= Min (8, 2) = 2
D1 satisfied and next allocation is made at (2, 2):
X22 = Min (a2 – X21, b2)
= Min (8-2, 9)
= Min (6, 9) = 6
O2 availabilities are allocated, next allocate at (3, 2):
X32 = Min (a3, b32 – X22)
= Min (7, 9 – 6) = Min (7, 3) = 3
D2 Satisfied, next allocate at (3, 3) as:
X33 = Min (a3 – X32, b3)
= Min (7-3, 18) = min (4, 18) = 4
O3 Satisfied, Allocate at (4, 3) as:
X43 = Min (a4, b3 – X33)
= Min (14, 18, -4) = Min (14,14) = 14
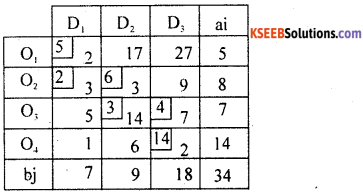
The Initial Basic feasible solution (I. B. F.S) is:
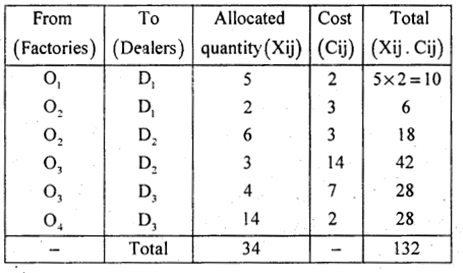
Answer:
2. Solution by Matrix -minima method: From the given T.P:
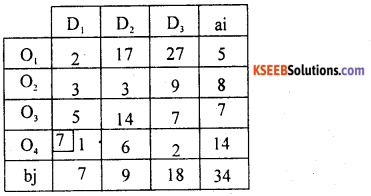
By M.M.M / least OR lowest cost entry Method: The lowest cost in the cost matrix is 1 at (4, 1): The allocation is X41 = Min (a4, b1)X41 = Min (14,7) = 7
D1 is satisfied so, delete D1 and replace (O14– X41)= 14-7 = 7.
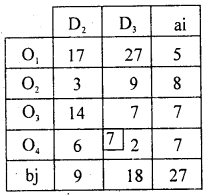
The lowest cost is 2 at (4,3) in the first table. Allocate X43 = Min (7,18) = 7 and replace 18 by (18 – 7) = 11. O4 is satisfied and delete and the reduced table is:
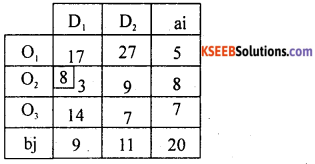
In the above reduced cost matrix the least cost is 3 at (2,2) of first table. So, allocate as X22 = Min (8, 9) = 8 and replace. (9 – 8) = 1 and delete O2.
There ducad cost matrix is:
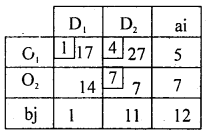
The next allocation is made at the cell (3,3) which has least cost 7.
Allocate X33 = Min (7,11) = 7. Replace 11 by (11 – 7) = 4 O3 is satisfied, since remaing only one origin, allocate all allocation in the same cost matrix.
Allocate, at next least cost 174, as X12 = Min (5,1)= 1 and replace 5 by (5- 1) = 4 as D2 is satisfied next allocate as X13 = Min (4,4) = 4.
All availabilities and requirements are satisfied.
The initial basic feasible solution is:
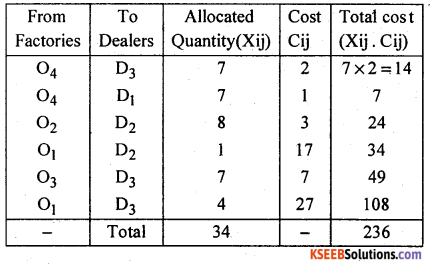
The total transportation cost = Rs. 236.
![]()
Game Theory
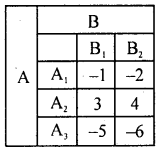
Question 1.
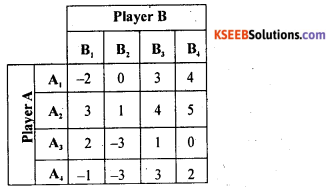
Find the value for the following game using maximin minimax method. Also write the best strategies for A and B. Player B
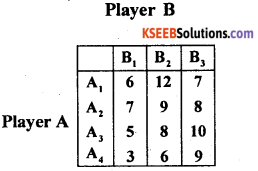
Answer:
The minimum payoff in each row of the pay off matrix is circled.
The maximum payoff in each column is boxed.
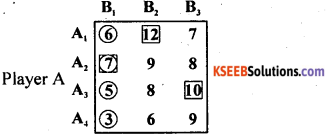
The pay off 7 is circled as well as boxed.
∴ Saddle point occurs at (2, 1)
The suggested solution is (Pure strategy)
The best strategy for A is A2 and for B is B1 value of the game V = 7.
Question 2.
Solve the following game. In the game fair?
Answer:
By maximin – minimax principle
The minimum pay off in each row is Circled.
The maximum pay off in each column is boxed.
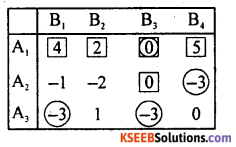
Here, minimum payoffs and maximum payoffs are repeated and hence both are circled and boxed.
The payoffs ‘0’ is circled as well as boxed.
∴ Saddle point occurs at (1, 3)
The suggested solution is (The pure strategy)
The best strategies are A1, B3.
Value of the game V = 0
The game is fair.
Question 3.
Two persons A and B without showing each other, place a coin each on the table. If the coin happens to be of the same denomination player A will take both of them. If they happen to be of different denominations, Player B will take both of them. Suppose Player A has a few one rupee coins and two rupee coins and suppose player B has few one – rupee, two-rupee and five-rupee coins.
Write down the payoff matrix of A. Does the game have saddle point ? If so, write down the solution.
Answer:
The pay off matrix of player A is
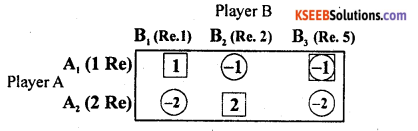
The minimum pay off in each row is Circled.
The maximum pay off in each column is boxed.
Here row minimums are repeated. .
The pay off ‘-1’ at (1, 3) is circled as well as boxed, which is the saddle point.
The solution to the games is:
The best strategies for player A is A1, and for B is B3 i.e., player A always use to play with 1 Re coin and player B with 5 Re. coin.
Value of the game V = -1.
Question 4.
Player A writes one of the numbers 1, 2 and 3 on a piece of paper and keeps the figures hidden in his paper. And without knowing which number he has written, player B writes one of the numbers 2 and 5 on the same paper. Then if the two numbers written by the two players are added. If this sum is odd, A pays Rs. 5 to for B otherwise B pays Rs. 10 to A. Write down the pay off matrix of A. Does the game have a saddle point.
Answer:
The payoffs matrix of player A is:
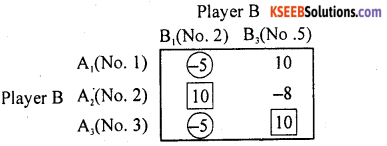
By maximin-minimax principle.
The minimum payoff in each row is Circled.
The maximum payoff in each column is boxed.
Here columns maximums are repeated.
Here none of the payoff is circled as well as boxed.
∴ The game has no saddle point.
The suggested strategies is mixed strategy.
Question 5.
Solve the following game using dominance principle. Also find the best strategies of A and B.
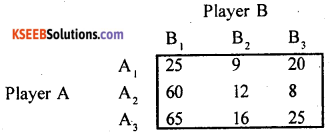
Answer:
By principle of dominance, In the pay off matrix, each pay off strategy A3 are greater than, each pay off strategy of A2 Therefore A3 dominates A1 and A1 is deleted.
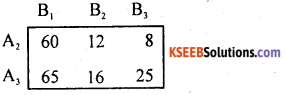
Here, each pay off (in 2nd column) of B2 strategy are less than, each pay off of strategy B1.
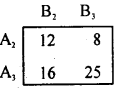
A3 dominate A2, so delete A2
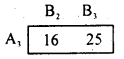
B2 dominates B3 so, delete B3
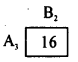
Thus, the saddle point occurs at (3, 2). The suggested solution to the game is:
Strategies for players A and B are (A3, B2)
Value of the game V = 16
![]()
Question 6.
Find the solution of the game by the principle of dominance for the following payoffs matrix of A.
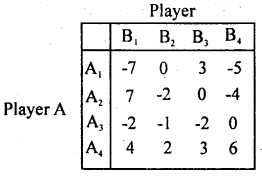
Answer:
By principle of dominance, A4 dominates A3, and A1. So, delete A1, A3.

B2 dominates B1 and B3. So, delete B1, B3
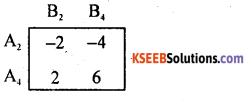
A4 dominates A2, delete A2,
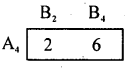
B2, dominates B4 delete B4.
Saddle Point occurs ar (4, 2).
∴ Suggested pure strategies for player A and B are (A4, B2) value of the game V = 2.
Question 7.
Solve the game using dominance principle :
Answer:
By principle of dominance, A2 dominates A1, A3 & A4. So delete A1, A3 & A4
B2 dominates B1 B3 & B4, so, delete B1 B3 & B4.

Saddle point occurs at (2, 2)
∴ The suggested pure strategy for the players are (A2, B2).
Value of the game V = 1.
Question 8.
Following is the pay-off matrix of player A.
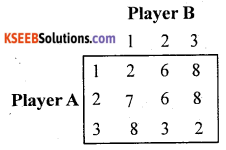
Find the solution of the game using the principle of Dominance.
Answer:
By Principle of dominance, 2nd strategy of player A dominates, 1st strategy. So, delete 1.
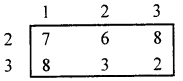
2nd column dominates 1st column, So delete column 1.
2nd row dominates 3rd row, delete 3rd row.
2nd column dominates 3rd column, so delete 3rd column.
![]()
Saddle point occurs at (2, 2)
∴ The suggested pure strategies for player A and B are, for player A -2, for player B- 2.
Value of the game V = 6.
Replacement Problems
Question 1.
The cost of a machine is Rs. 12000. The maintenance cost and resale value per year of the machine is given below.

When should the machine be replace
Answer:
Here, purchase price ; P = Rs. 12000
Let Ci be the maintenance cost during the year and Sn be the resale value.
Then, Average annual cost is A(n) = \(\frac { T }{ n }\) , Where T = (P – Sn) + ΣC ; and n = no. of years.
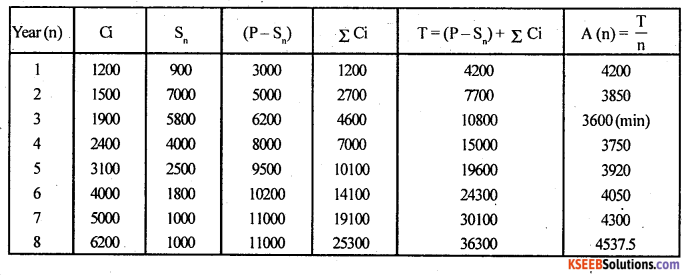
Here, Average annual cost A(n) is minimum for n = 3.
∴ The optimal replacement age is 3 years,
i. e., The machine should be replaced for every 3 years.
Minimum annual average cost is Rs. 3600
Question 2.
A machine costs Rs. 36,000. Its resale value and maintenance cost at different years are given below:

Resale Value (Rs.) 28,000 22,000 20,000 18,000 17,000 15,000
Find out when the machine should be replaced.
Answer:
Given : cost/purchase price ‘P’ = Rs. 36,000
Let Ci be the maintenance cost, Sn be the resale value and n be the number of years.
Average annual cost : A(n) = \(\frac { T }{ n }\) ; where T = (p – Sn ) + ΣCi
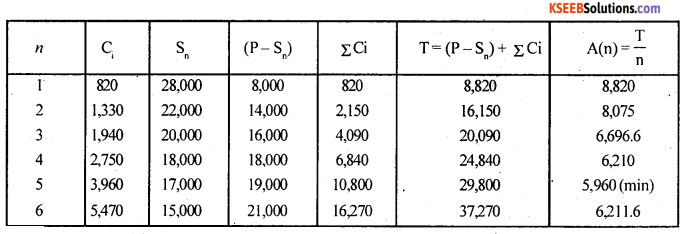
Here, average annual cost A (n) is minimum for n = 5.
∴ The optimal replacement age is 5 years i.e. the machine should be replaced for every 5 years.
Minimum annual average cost is Rs. 5,960.
![]()
Question 3.
A machine costs Rs. 80,000 and the operating cost is estimated to be Rs. 5000 for the first year and increases by Rs. 7000 every year for next five years. Determine the optimum period for replacement of the machine, assuming that the machine has no scrap (Resale) value.
Answer:
Here the machine cost = P = Rs. 80,000 and since resale value Sn = 0 ; the depreciation (P – Sn) = 80000 for all the years and let Ci be the operating cost.
The Average annual cost A(n) = \(\frac { T }{ n }\); Where T = Total cost = (P – Sn) + ΣCi and n = no. of years.
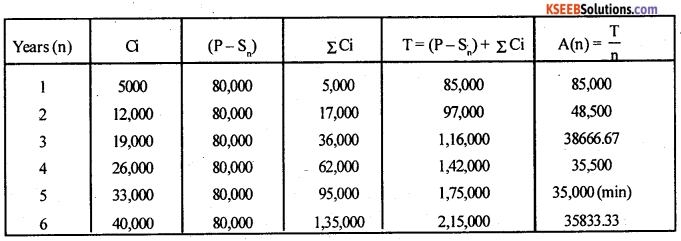
Here, Average annual cost A(n) is minimum for n = 5.
∴ The optimum replacement age is 5 years,
i.e., the machines should be replaced at the end of 5 years.
Minimum annual average cost = Rs. 35000
Question 4.
A tractor owner finds from the past records that maintenance cost and depreciation cost per year of the tractor whose purchase price is Rs. 1,50,000 are as follows:

Determine at which time is it possible to replace the tractor.
Answer:
Given: P = Rs. 1,50,000, let maintenance cost be Ci during the year and depreciation be (P – Sn), where. Sn be the resale/ scrap value.
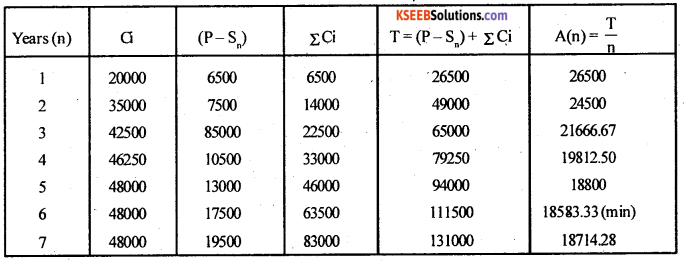
Here, Average annual cost A(n) is minimum for n = 6.
∴ The optimal replacement age is n = 6 year, i.e., the tractor should be replaced after using it for 6 years. The optimum Average annual cost is Rs. 18583.33.
Inventory Problems
Question 1.
What are the advantages and disadvantages of maintenance of inventory?
Answer:
Advantages:
- Bulk production decreases costs of production, transportation, maintenance, etc.
- Instant/uninterrupted supply of goods to customers.
- Inventory gives profit due to increase in market price.
- Inventory decreases the setup cost.
Disadvantages:
- Ware house rent.
- Interest on invested capital.
- Labour on maintenance of inventory.
- Maintenance of records.
- Loss due to fall in price, deterioration and depreciation, etc.
Question 2.
A firm has an annual demand of 3000 units of raw materials. The setup cost is Rs. 25 per order and holding cost is Rs. 2 per unit/year. Determine
1. optimal order quantity
2. number of order per year
3. Annual average inventory cost.
Answer:
Given: R = 3000, C3 = Rs. 25/order ; C1 = Rs. 2 per unit/year.
Here shortage cost C2 is not given use EOQ model I
1. (/) EOQ : Optimal order Quantity = Q° = \(\sqrt{\frac{2 \mathrm{C}_{3} \mathrm{R}}{\mathrm{C}_{1}}}=\sqrt{\frac{2 \times 25 \times 3000}{2}}\) = 273.86 = 274 units
2. Number of orders n° = \(\frac{1}{t^{0}}=\frac{R}{Q^{0}}=\frac{3000}{273.86}\) , Here t° = \(=\frac{Q^{0}}{R}\)
n° = 10.95 = 11 orders per year
3. Annual average inventory cost.
C (Q°) = \(\sqrt{2 \mathrm{C}_{1} \mathrm{C}_{3} \mathrm{R}}=\sqrt{2 \times 2 \times 25 \times 3000}\) = Rs. 547.72/year
Question 3.
A dealer has to supply 15 computer to a retail customer every week. He maintain an inventory in which the maintenance cost is Rs. 100 per unit per year. The ordering cost is Rs. 350 per order. Find EOQ, the optimum re-scheduling time and the optimum average cost.
Answer:
Given: R = 15/week ; and
R = 15 × 52 per year.
C1 = Rs. 100 per unit/year.
C3 = Rs. 350 per order.
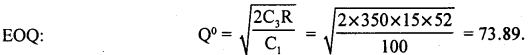
Q° = 73.89 units
Re-scheduling time t° = \(\frac{Q^{0}}{R}=\frac{73.89}{15 \times 52}\) = 0.0947 years.
i.e., 66 units should be ordered approximately every 1 month.
The optimum average cost/minimum average cost :
C(Q°) = \(\sqrt{2 \mathrm{C}_{1} \mathrm{C}_{3} \mathrm{R}}=\sqrt{2 \times 100 \times 350 \times 15 \times 52}\) = Rs. 7389.18 per year.
![]()
Question 4.
A manufacture has to supply 80 units of his product every month to a customer. Capital cost is Rs. 800 per unit. Holding cost is 12% per year of capital cost. Shortages are not allowed. Cost of setting up machines for production is Rs. 300. How frequently should production be made so that inventory is most economical?
Answer:
Given: R = 80 units per month and R = 80 × 12 = 960 units per year.
P = Capital cost = Rs. 800 per unit.
I = Holding cost per unit per year = 12%.
∴ C1 = carrying cost per unit = PI = 800 × 12% = Rs. 96 per year.
C3 = Set up cost = Rs. 300 per order.
Economic order quantity : Q° =\(\sqrt{\frac{2 C_{3} R}{C_{1}}}=\sqrt{\frac{2 \times 300 \times 960}{96}}\)
∴ Q° = 77.46 = 77 order.
Reorder time is t° = \(\frac{Q^{0}}{R}=\frac{77.46}{960}\) = 0.0807 years.
i.e., t° =0.0897 × 365 = 29 days (approx)
Frequency of order is n° = \(\frac{1}{t^{0}}\) = 12.39 per year
Minimum average cost is
C(Q°) = \(\sqrt{2 \mathrm{C}_{1} \mathrm{C}_{3} \mathrm{R}}=\sqrt{2 \times 96 \times 300 \times 960}\) =7436.13
C(Q°) = Rs. 7436.13 per year
Question 5.
If the demand is 300 units per year, inventory holding cost is Rs. 8 per unit per year, shortage cost is Rs. 10 per unit per year and setup cost is Rs. 500 per replenishment. Determine EOQ and the maximum shortage level.
Answer:
Given : R = 300 unit per year,
C1 = Rs. 8 per unit per year.
C2 = Shortage cost = Rs. 10 per unit per year,
C3 – Setup cost = Rs. 500 per replenishment. .
The economic order quantity is
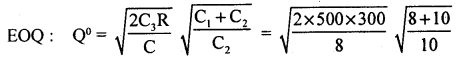
Q° = 259.80 = 260 units.
The maximum shortage level is –
(Q° – S°) Here S°: Maximum inventory level.
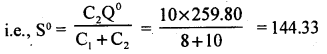
∴ (Q°-S°) = 2.59.80- 144.33 =115.46
Maximum shortage level is 115 units.
Question 6.
A dealer supplies the following information with regard to a product dealt by him. Annual demand = 4500 units. Ordering cost = Rs. 20. Holding cost = Rs. 2.00. Shortage Cost = Rs. 12. Determine EOQ and Total variable cost.
Answer:
Given: R = 4500 units ;
C3 = Rs. 20
C1=Rs. 2,
C2 = Rs 12
The economic order quantity is –
Q° = 1052 units (Approx)
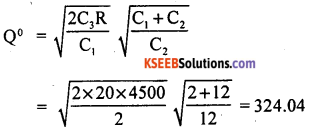
i.e., Q°= 324 Units.
Total variable cost/minimum average cost is
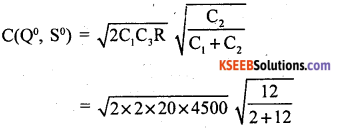
C(Q°, S°) =Rs. 555.49
Question 7.
A Factory requires 2000 units for an item per year. Purchase cost is Rs. 30, the setup cost is Rs. 200. The carrying cost is Rs. 8 per item/year. If the shortage cost is Re. 1 per item/month. Determine
1. EOQ
2. Minimum average cost.
Answer:
Given : R = 2000 ; P = Rs. 30 C3 = Rs. 200
C2 = Re. 1 per item/month.
i.e„ C2 =1><12= 12/year. C1 = Rs. 8 per item per year.
(Here shortage cost is given, so use EOQ model II)
1. Economic order quantity is –
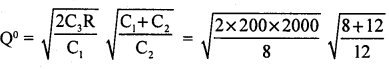
Q° = 408.25 units
2. Minimum average cost is –
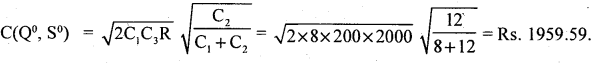
Question 8.
The annual demand for an item is 3000 units. Capital cost is Rs. 7 per unit. Inven¬tory carrying cost is 20% of capital cost per annum. If set up cost is Rs. 150, determine
1. EOQ
2. Number of orders per year
3. Optimal cost
Answer:
Given R = 3000, p = 7,1 = 20%
c3 = 150. (Shortages are not given use EOQ model I)
1. EOQ : \(Q^{0}=\sqrt{\frac{2 C_{3} R}{C_{1}}}\)
C1 = p1 = 7 × \(\frac { 20 }{ 100 }\)
\(Q^{0}=\sqrt{\frac{2 \times 150 \times 3000}{1.4}}\) = 801.78 units
2. n° = \(\frac{R}{Q^{0}}=\frac{3000}{801.78}\) = 3.4 orders
3. C(Q°) = \(\sqrt{2 \times 150 \times 3000 \times 1.4}\) = Rs. 1122.50
![]()