Students can Download Maths Chapter 11 Congruency of Triangles Ex 11.2 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 11 Congruency of Triangles Ex 11.2
Question 1.
In the adjoining figure PQRS is a rectangle. Identify the congruent triangles formed by the diagonals.
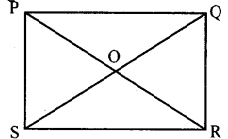
Answer:
Δ PSR ≅ Δ PQR, Δ POQ ≅ Δ SOR
Δ SPQ ≅ Δ SRQ, Δ POS ≅ Δ QOR
Question 2.
In the figure ABCD is a square. M, N, O & P are the midpoints of sides AB, BC, CD and DA respectively. Identify the congurent triangles.
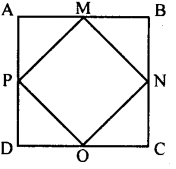
Answer:
Δ APM ≅ Δ BMD ≅ Δ CNO ≅ Δ DOP
Question 3.
In a triangle ABC, AB = AC. Points G on AB and D on AC are such that AE = AD. Prove that triangles BCD and CBE are congruent.
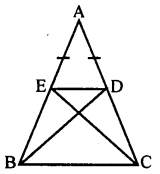
Answer:
In the figure AB = AC (data)
∴∠ABC = ∠ACB
[Base angles of an isosceles triangle]
AB = AC(data)
AE = AD(data)
AB – AE = AC – AD (Axiom 3)
BE = DC
In Δ BCD and Δ CBE
∠BCD = ∠EBC
BE = DC (Proved)
BC = BC (Common side)
∴ Δ BCD= Δ CBE [SAS postulate]
Question 4.
In the adjoining figure the sides BA and CA have been produced such that BA = AD and CA = AE prove that DE || BC (hint : use the concept of alternate angles.)
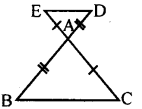
Answer:
Δ AED and Δ ABC
AE = AC (data)
AD = AB (data)
∠EAD = ∠BAC
[Vertically opposite angles]
∴ Δ AED = ABC
[SAS postulate]
∴ ∠AED = ∠ACB [Congruent triangle property]
But these are alternate angles.
∴ DE || BC
Consequences of SAS postulate.