Students can Download Maths Chapter 11 Congruency of Triangles Ex 11.3 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 11 Congruency of Triangles Ex 11.3
Question 1.
In a Δ ABC, AB = AC andlA.= 50° find ∠B and ∠C.
Answer:
∠A+ ∠B + ∠C = 180°
(Sum of the angles of a triangle is 180° )
50 +∠[B + ∠B = 180°
∠B = ∠C Base angles of an isosceles triangle
50 + 2∠B= 180°
2∠B = 180 – 50
2∠B = 130°
∠B = \(\frac{130^{\circ}}{2}\)
∠B = 65°
∠B = ∠C = 65°
Question 2.
In AABC,AB = BCand|B = 64°find|£,
Answer:
AB = BC [data]
∴ ∠C = ∠A [Theorem 1]
∠A + ∠B + ∠C = 180°
(Sum of the angles of a triangle is 180°)
∠C + 64 + ∠C = 180° [∠A = ∠C]
64 + 2∠C = 180°
2∠C = 180 – 64
2∠C = 116
∠C = \(\frac { 116 }{ 2 }\) = 58°
Question 3.
In each of the following figure find the value of x :
i.
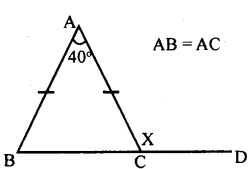
Answer:
In ∆ABC, AB = AC
∴ ∠ABC = ∠ACB
∴ ∠BAC + ∠ABC + ∠ACB = 180°
(Sum of the angles of a triangle is 180°)
40 + ∠ABC + ∠ABC = 180°
(∠ABC =∠ACB)
40 + 2∠ABC = 180°
2∠ABC = 180 – 40
2∠ABC = 140°
∠ABC = 70°
∠ACB = ∠ ABC = 70°
∠ACB + ∠ACD = 180°
70 + x = 180°
x = 180 – 70
x = 110°
ii
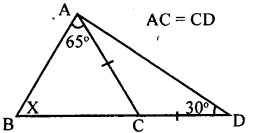
AC = CD
∠CAD = ∠CDA
∠CAD = ∠CAD = 30°
∠ACD + ∠CAD + ∠CDA = 180°
(Sum of the angles of a triangle is 180°)
∠ACD + 30 + 30=180°
∠ACD + 60=180°
∠ACD = 180-60
∠ACD = 120°
∠ACD = ∠BAC + ∠ABC
120 = 65° + x
120 – 65 = x
55 = x
x=55°
iiii
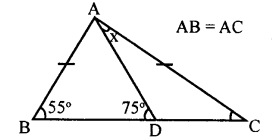
Answer:
AB = AC
∠ABC = ∠ACB = 55° [Theorem l]
Exterior ∠APB = ∠DAC +∠ACD
75 = x + 55
75 – 55 = x
20 = x
x = 20°
iv.
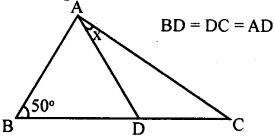
BD = DC = Ad
BD = DC = AD & ∠ABD = 50 °
∠ABD = ∠BAD(Th. l)
∠BAD = 50°
∠ABD + ∠BAD + ∠ADB = 180°
50 + 50 +∠ADB = 180°
∠ADB = 180 – 100 = 80°
∠APB = 80°
∴ ∠APB +∠ADC = 180°
80 +∠ADC = 180°
∠ADC = 100°
Now AD = DC
∴∠DAC = ∠DCA = x°
∴ x + x +∠ADC = 180°
2x + 100 = 180°
2x = 180-100=80°
x=40°
Question 4.
Suppose ABC is an equilateral triangle. Its base BC is produced to D such that BC = CD.
Calculate: l.∠ACD
2.∠ADC
Answer:
∠ABC = ∠ACB = ∠BAC = 60°
(ABC is an equilateral triangle)
∠ACB +∠ACD = 180° (Linearpoint)
60 + ∠ACD = 180°
∠ACD = 180 – 60
∠ACD = 120°
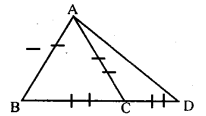
In ∆ACD,AC=CD
∠ CAD = ∠CPA (Theorem l)
∠ACB +∠ACD = 180° [linear pair]
60° +∠ACD = 180°
∠ACD = 180° – 60° = 120°
∠ACA +∠CAD + ∠CDA = 180°
2∠CDA = 180 – 120°
2∠CDA = 60°
∠CDA = \(\frac { 60 }{ 2 }\) = 30°
∠CDA = 30
Question 5.
Show that the perpendicular drawn from the vertices of the base of an isosceles triangle to the opposite sides are equal. ,
Answer:
Data : In ∆ABC, AB = AC,
BD ⊥AC & CE⊥ AB
To prove : BD = CE
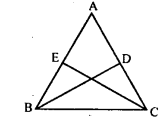
Proof:
In ∆ABC, AB = AC [data]
∠ABC = ∠ACB [Theorem l]
In ∆EBC and ∆DCB
∠EBC =∠DCB( Base angles )
∠BEC = ∠CDB [= 90° ]
BC = BC (Common side)
∆EBC = ∆DCB [ASA postulate]
BD = CE [Corresponding sides]
Question 6.
Prove that an ∆ABC is an isosceles triangle if the altitude AD from A on BC bisects BC.
Answer:
In ∆ADB and ∆ADC
AD = AD [Common side]
∠APB =∠ ADC [90° ]
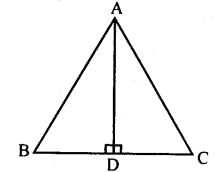
BD = DC [AD bisects BC]
∴∆ADB ≅ ∆ADC [SAS postulate]
∴AB = AC [Correspondingsides]
∴∆ ABC is an isosceles triangle
Question 7.
Suppose a triangle is equilateral, prove that it is equiangular.
Answer:
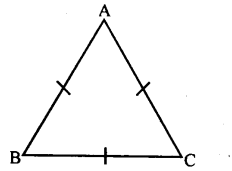
To prove: ∠A = ∠B = ∠C
Proof: In ∆ABC, AB = BC
∠C = ∠B [Theorem l]….(i)
BC = AC
∠A =∠B [Theorem l]…(ii)
From (i) and (ii)
∠A =∠B = ∠C
∆ABC is equiangular